抓事物本質 促思維素質
——例談復數(shù)在解題中的應用

◎王愛華

我們知道在數(shù)學解題中，揭示知識點的本質，題目的特征、結構等，是解題的一個關鍵，如：復數(shù)，就其本質來說，它是在實數(shù)的基礎上擴充而來，任意復數(shù)，無論是由實部與虛部兩部分組成的，還是由模與幅角相結合的，都是由一對實數(shù)確定，就其表現(xiàn)形式，可用復平面上的點、復平面上的向量來表示，它們之間不僅存在對應關系，且可相互轉化，有著豐富的內涵。只要充分認識復數(shù)的本質，在復數(shù)集內就可化“實”為“虛”，“虛”中求“實”。因此，“虛”“實”互求，既相對，又相輔。今略舉幾例說明之。

一、在求三角函數(shù)值中的應用

【例】已知 α、β、γ是公差為2π/3的等差數(shù)列，求 sinα+sinβ+sinγ與 cosα+cosβ+cosγ的值。

分析：α、β、γ之間的關系為 β=α+2π/3，γ=β+2π/3=α+4π/3，而所求式子為三個角的同名函數(shù)之和，由此，啟發(fā)我們運用復數(shù)三角式的加法與乘法來處理比較好。

解：設 Z1=cosα+isinα，則

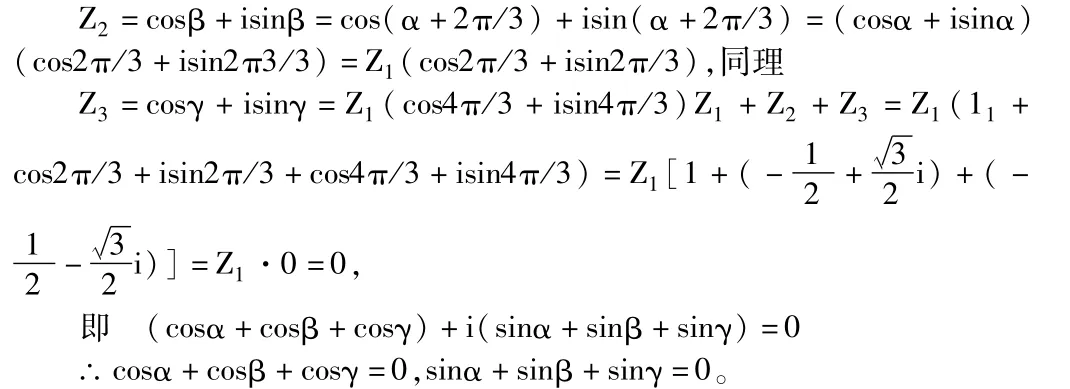
點評：這里應用了復數(shù)三角式化簡角呈規(guī)律性變化的兩弦函數(shù)和的式子這一本質特征，很湊效，它能把正弦函數(shù)和的值以及余弦函數(shù)和的值同時求出。

二、在證明不等式中的應用

【例】a、b、c∈R，且 a+b+c＞0，

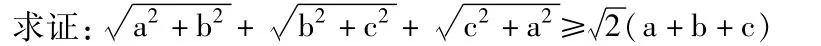
分析：由題目結構特征，聯(lián)想到復數(shù)模，再聯(lián)想到復數(shù)不等式，通過模的運算及復數(shù)不等式得證。

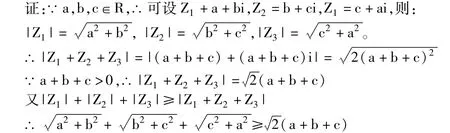
點評：由于題目的特征、結構，引入復數(shù)的模及復數(shù)不等式（實質上是一個實數(shù)不等式），應用了復數(shù)的模的本質特征，使得一個較繁的無理不等式化繁為簡。

三、在求軌跡方程中的應用

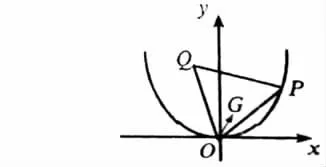
【例】在拋物線y=x2上有一個動點P，以OP為一邊，按逆時針方向作正ΔOPQ，求此三角形中的心G的軌跡方程。

分析：這是一個線段旋轉問題，OG可視為OP旋轉，并按比例縮短而得，從而聯(lián)想到復數(shù)乘法的幾何意義，再通過復數(shù)相等找到了第一動點與第二動點的關系，問題得以解決。

解：建立直角坐標系如圖，設 G（x，y），P（x′y′）在復平面上作向量，則按逆時針方向轉30°，模縮為原來的即得到，兩者的對應復數(shù)有關系式

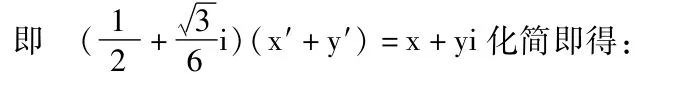
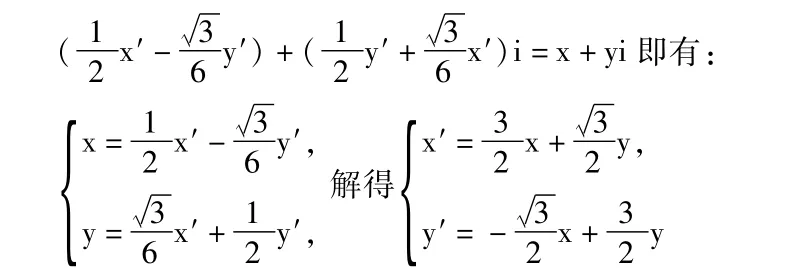
代入點P滿足的方程y=x2化簡即得點G的軌跡方程為：9x2+6。

點評：這是一個旋轉問題，一般來說，緊扣復數(shù)乘法的幾何意義和復數(shù)相等的充要條件可“實”“虛”互化這一本質特征，就便于解決問題。

四、在證明三角恒等式中的應用

【例】求證：

點評：這里通過觀察思考題目的結構特征，充分應用了復數(shù)運算和復數(shù)相等的本質特征。

五、在求反三角函數(shù)值中的應用

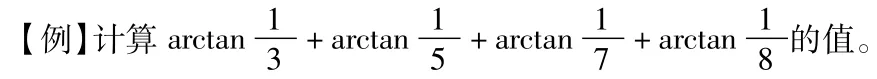
分析：實質上這是一個實數(shù)問題，但實數(shù)包含于復數(shù)，且題中所含的量在復數(shù)中具有輻角主值的意義，數(shù)學中用構造某些復數(shù)，使其輻角成為所求式子中的角度，從而通過復數(shù)運算性質而求角。

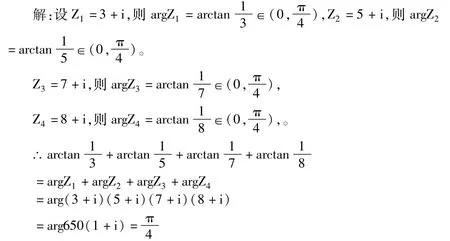
點評：構造復數(shù)使它們的輻角分別為組成題中的各角，應用了復數(shù)運算的本質特征，從而化“實”為“虛”去解題，再從“虛”中求“實”求得輻角。

關于復數(shù)在解題中的應用題很多，以上只舉了其中常見的幾種，以說明抓住事物的本質，去解決矛盾這一觀點。筆者認為，在教學中，不論傳授知識、還是傳授方法、培養(yǎng)能力等方面，只要堅持這一辨證的觀點，不僅有利益提高教育教學質量，而且在培養(yǎng)學生思維素質方面都進入了更深一個層次，無疑對提高學生的數(shù)學素質起著重要的促進作用。