基于數學核心素養的深度學習實踐初探
——以“平面向量的分解定理”概念教學為例
◎汪園娣
基于數學核心素養的深度學習是指基于數學核心素養之上的理解學習,學習者能夠批判性的學習新的思想和事實,并將它們融入原有的認知結構中,能夠在眾多思想間進行聯系,并能夠將已有的知識遷移到新的情境中,作出決策和解決問題。基于數學核心素養的深度學習是圍繞數學抽象、邏輯推理、數學建模、數學運算、直觀想象和數學分析六大核心內容[1],引起學生的高級思維和認知,從而形成對知識的理解和遷移,最終培養學生的批判性思維和創新意識。筆者以“平面向量的分解定理”一課概念教學為例,結合教學實踐,以深度學習理論為指導,在課堂教學中探索一套適應于新高考背景下基于數學核心素養的深度學習模式。
教學目標
以探究的形式體驗平面向量分解定理的發現和形成過程;
理解平面向量分解定理,體會由特殊到一般的思想,感悟數學的化歸思想。
教學重點和難點
重點:平面向量的分解定理
難點:平面向量分解定理的發現和形成過程
教學過程
本節課導入環節,遵循學生的認知規律,在原有的認知體系中,根據已學內容向量的坐標直接導入。[2]通過課堂對話,回顧坐標的形成過程,得出基于兩個基本單位向量的向量的正交分解,為本課探究做鋪墊。
環節一 坐標導入
提問1:平面任一的坐標怎樣表示?回顧向量的坐標表示的由來。
提問2:向量的坐標表示(代數角度),是通過怎樣的向量分解(幾何角度)實現的?
提問3:平面內任一向量的正交分解唯一嗎?
本環節注重元認知發展,開展深度學習,鼓勵學生以探究的方式和合作的模式進行新知識和信息與新問題的解決。注重學生對于現有知識的反思,并強調新知識內化之后,與固有知識結構之間的聯系。
環節二 特例過渡
適當改變上述正交分解的條件,通過數學活動的開展,體驗一般情形下正交分解的過程。
數學活動:上述正交分解中的“兩個基本單位向量”改為“給定兩個互相垂直的非零”,能否進行分解?分解有何特點?
數學發現:“互相垂直”條件改變可以分解嗎?
數學活動的開展,讓學生發現基于給定兩個互相垂直的非零向量,可以進行正交分解。對于知識的處理,是基于學生對知識的理解,由特殊到一般,循序漸進,在此基礎上進行知識的獲取和解決問題的策略。深度學習的必要前提是學生對于知識有著比較濃厚的興趣,有探究的欲求。
環節三 定理探索
基于尋找向量分解的條件,進一步引導,激發學生進一步探索的欲望。
(一) 數學發現
探究1:除正交分解外,你還可以對平向量進行怎樣的分解?
探究2:對于滿足什么條件的兩個給定向量,平面內任一向量可以分解?
數學發現:類比向量的正交分解,當“兩個互相垂直的”變成“給定平面上兩個不平行向量”,你有什么發現?
給定一組不垂直的非零向量,親身經歷向量分解的過程,目的在于尋找向量進行分解的條件。將已有認知結構中知識遷移作用于其它情境中,特殊到一般,通過類比發現,給定平面上兩個不平行向量,該平面上任一向量都可以表示成這兩個不平行向量的線性組合。
(二)數學體驗
活動一 給定兩個方向,將一個分解成兩個向量的和.
活動二是平面內兩個不平行的向量,是該平面內的任意一個非零向量,之間的關系.
通過數學發現,得出向量分解的條件;開展數學活動,經歷平面向量的分解。初步形成:平面內的任意一個非零都可以表示成這兩個不平行的線性組合,即分解可行.
(三)數學探究
從兩個特殊向量出發,師生共同完成這兩個特殊向量的分解,得出可以分解且唯一。

探究三 當平面上兩個不平行的取定時,任一向量的分解唯一嗎?
探究的思路始終遵循學生的認知結構,由已知到未知,由特殊到一般,進行邏輯推理,得出當平面上兩個不平行的向量取定時,任一向量的分解唯一。學生結合自身的內在需求對學習材料進行比較深刻的思考和探究,通過使用與學習材料相適應的學習方法,對知識進行批判性的接收和創造性的使用,從而實現學習的真正意義,達到深度學習的效果。
環節四 定理形成
學生通過定理探索,經歷數學發現、數學體驗、數學探究,概括平面向量分解定理:

探究一 條件中“不平行向量”,改為“平行向量”,如何?
探究二兩繩子可以以任意角度懸掛同一重物,重物因為具有重力,會對兩繩子產生拉伸效果。
思考:兩根繩子的懸掛的角度不同,重力分解的結果如何?
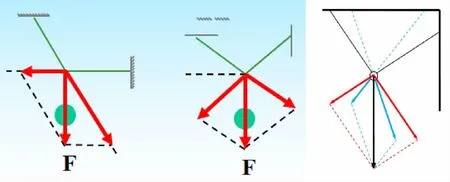
探究三對于給定的一組基,向量的分解是否唯一?
以探究的形式體會定理的涵義,從物理實例出發,在熟悉的問題情境中,經歷物理問題數學化的過程,感悟其中蘊含的數學原理,加深數學理解,得出平面上任一向量可以有無窮多種分解,即有無數組基,且對給定的一組基分解唯一。
環節五 定理應用
通過定理探索,得出平面向量分解定理,如何夯實該定理,通過下面的幾個實例來實現。
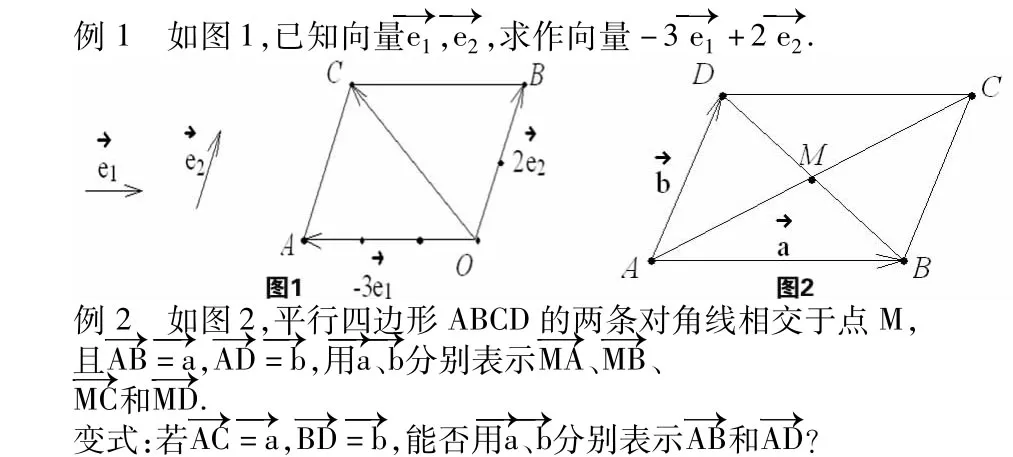
解決實際問題,體會基向量思想在運算化簡中的作用,可以讓向量運算更加有目的性,體會平面向量分解定理的意義。深度學習,注重對于知識的解釋與剖析,并且隨著知識種類的不同而有著不同的內化模式。
教學后記:以探究的形式體驗平面向量分解定理的發現和形成過程,教學緊緊圍繞向量分解展開。在教學過程中,學生無論經驗的積淀、基本思想的形成,還是數學抽象能力、邏輯推理、數學建模的培養,都離不開學生的主動參與、獨立思考和親身實踐,離不開學生的自我建構。因此,學生發展所必需的數學核心素養是學生親身經歷數學化活動之后所積淀和升華的產物,這種產物對學生在數學上的全面、和諧、可持續發展起決定作用。[3]
課堂教學采用探究形式,有利于培養學生的發現問題解決問題的能力,通過親身實踐探索獲得的知識,實現自我建構,以實現深度學習。在實際操作中,學生思維一旦打開,探究問題方向多樣,而易脫離教學主線,影響教學進度的推進,需要提前預想到多種可能情況,合理安排探究內容和時間,以達到更好的教學效果。
[1]教育部課程標準修訂組.普通高中各學科核心素養一覽表 [EB/OL].http://learning.sohu.com/20160422/n445632409.shtml
[2]吳秀娟,張浩,倪廠清.基于反思的深度學習:內涵與過程[J].電化教育研究,2014(12):23-28.33.
[3]孔凡哲.學會數學化切實提升數學學科素養[J].小學數學教師,2015(6):孔凡哲.學會數學化切實提升數學學科素養[J].小學數學教與學,2015,(9).

