電能表的不確定度評定與表示
李金生
(河鋼集團唐鋼公司信息自動化部 河北 唐山 063000)
1 引言
凡是測量都會因客觀條件的存在而產生誤差,就測量結果而言其所針對的是無法確定的程度,也就是對測量結果可信賴度的一種判定。不確定度是一個參數,與測量結果緊密相關,并能夠真實反映測量結果的分散性,因此測量不確定度應該是完整測量中不可或缺的一個重要組成。
2 測量不確定度的評定
測量原理如圖1所示。
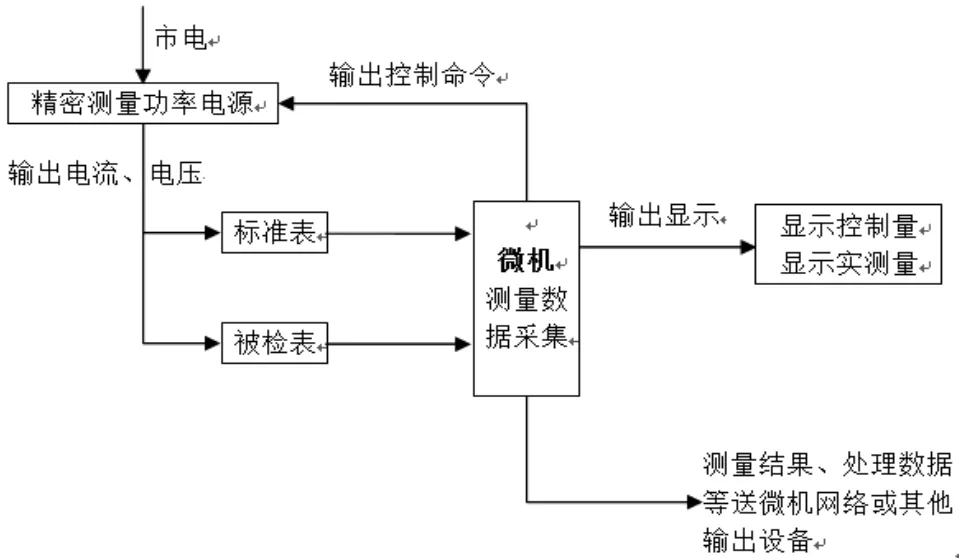
圖1 測量原理
2.1 分類
不確定度評定可分為A類和B類兩種,前者是通過對測列的統計分析法來完成評定的;后者則是通過不同于對側列的統計分析法來進行評定的。為了更好的區分不確定度評定,所以特意將他們分為AB兩類,但兩者之間并沒有本質的區別。A類和B類都是以概率分布為基礎,通過一組觀測數據導出的密度函數,所得到的就是A類不確定度;而B類不確定度標準評定則是針對的是一個事件發生的整體信任程度。
(1)A類評定
設測量值為xi(i=1,2,……,n),被測量X,測量次數為n。在統一條件下,通過計算得到平均值x-,標準偏差s(x)。當被測量估計值被鎖定為平均值時,便可以按照公式(1)計算出其所對應的A類不確定度UA(x)。
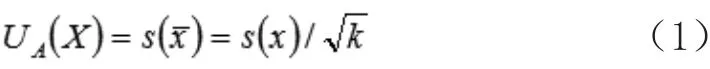
(2)B類評定
通過所有可以利用的相關信息,科學判斷測量結果的不確定度,最終得到估計的標準偏差,即為標準不確定度的B類評定。
①通過相關經驗和信息對測量的可能區間進行判斷,得到區間值(-a,a);
②對被測量值的概率分布進行假設;
③確定要求的概率p,然后基于概率分布原則對包含因子k進行估計,進而按照公式(2)得到B類不確定度UB。

2.2 電能表的校準

表1 三相電能表不確定度測量
在實際應用中會涉及到電能表的校準和檢定。要更好的完成這項工作,就必須熟練掌握電能表不確定度評定和表示原則,明確產生測量不確定度的根源是什么。認真分析電能表的校準過程,對校準過程中可能遇到的不確定度分量進行統計,以幫助評定工作的順利完成。如表1所示。
3 電能表的不確定度評定和表示
3.1 數學建模
處于對測量結果可信度的要求,校準和檢測安裝式電能表或標準電能表已經成為日常工作中必不可少的一項內容。人們最常用到的是標準表法,就是讓標準電能表和被檢測表同時進行電能值的測試,然后比較兩種測試所得到的結果,進而得到一個相對誤差,再以此為數據基礎進行數學建模,詳見公式(3):
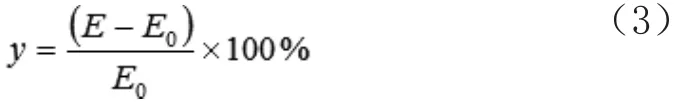
被檢測電能表的相對誤差值(%)用y來表示,其點能值用E0表示,點能值則用E表示。
3.2 分析測量不確定度的影響程度
從上一節中的數據建模中可以看出,被檢測電能表的電能值和標準表電能值是非常重要的兩個參數,所以對不定度的影響分析要從這兩點入手。
(1)u(E0)是標準電能表的標準不確定度,在對其進行評定的時候主要考慮兩方面的因素:一所選定的標準檢定裝置所允許的最大誤差是多少,由其引發的不確定分量是多少;二,凡是檢測裝置均存在檢測誤差,因此來自于檢定裝置的上級評定不確定度分量也會對電能表的不確定度分量造成影響,分量多大?
(2)u(E)是被檢電表能值的標準不確定度,能夠對其產生影響的因素也要分為兩部分:一,被檢測表誤差化整,引起一定的不確定度分量;二,被檢查電表多次重復被引入,引起的不確定度分量。
3.3 電能表不確定度的實例評定
對于電能表不確定度的評定上面已經做了詳細的闡述,下面將通過舉例的方式使分析更加形象和具體。
確定上級評定的不確定度U0=0.009%,k0=3,標注裝置選擇0.01級的三相標準電能表,被檢測電能表則為0.05級,均在220V電壓,5A電流,cosφ=1.0的條件下進行。
(1)因上級檢測裝置最大允許誤差引入的不確定度評定
±0.01%是0.01級的三相標準電能表的最大誤差,用B類評定法估計,它的區間半寬a=0.01%,在正態分布的情況下則可得到:
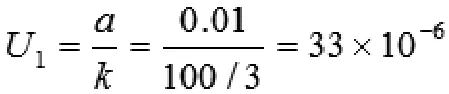
(2)因上級評定不確定度引入的不確定度評定
上級校準的不確定度U0=0.009%,k0=3,同樣采用B類評定估計它的區間半寬a=0.009%,則可得到:

(3)重復性測量所引入的不確定度評定
重復10次對0.05級的電能表進行測量,得到 的標準偏差,用A類評定法計算,得到:
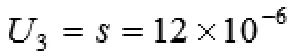
(4)誤差化整所引入的不確定度評定
依然選擇0.05級的電能表為被檢測對象,其誤差化整區間隔是0.005%,通過B類評定估計得到半寬且分布均勻的情況下:
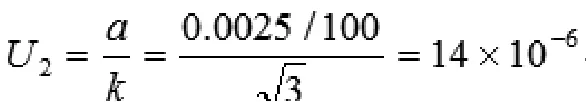
3.4 合成標準不確定度評定
A類和B類評定標準所占的不確定度分量決定了合成標準的不確定度評定。具體公式如下:
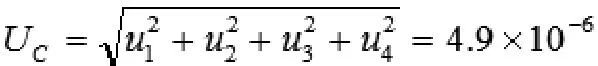
4 結論
本文通過概念分析、數據建模和實例舉證對測量不確定度的評定與表示做了簡單的闡述,并認識到評定流程包括A類和B類評定兩種方法。然后從日常工作中的實際情況出發,總結出所有能夠造成不確定度產生的因素,然后再借助具體的實例進一步證明電能表的不確定度評定流程的正確性,肯定其表現方法,這對于表征電能表的測量結果是非常有利的。
[1] 吳穎,王新剛,余宇紅,孟智剛.一種新型數字電能表檢測裝置的研究及其不確定度分析[J].供用電,2017,34(11):78-81+49.
[2] 王智,楊靜,蘇玉萍.電能表標準裝置量值傳遞方法的探究[J].湖南電力,2017,37(04):45-48+52.
[3] 周麗霞,丁恒春,袁瑞銘,張春雪,王學偉.電能表動態誤差測量系統及測量不確定度評定[J].電測與儀表,2016,53(08):81-85+118.
[4] 王淑平.電能表基本誤差測量不確定度評定[J].科技創新導報,2012,(28):105.

