基于數據集稀疏度的頻繁項集挖掘算法性能分析

肖 文,胡 娟

0 引言

頻繁項集挖掘(Frequent Itemset Mining, FIM)是最基礎的數據挖掘任務之一,是關聯規則、分類、聚集、離群點分析等眾多數據挖掘任務的重要組成部分,自它被提出以來[1],受到了越來越多的關注。經典的FIM算法可以分為三類:“產生-計數”類方法如Apriori[2]、DHP(Direct Hashing and Pruning)[3-4]、DIC(Dynamic Itemset Counting)[5]等;“模式增長”類方法如FP-Growth(Frequent Pattern Growth)[6]、LPTree(Linear Prefix Tree)[7]、FIUT(Frequent Items Ultrametric Trees)[8]、IFP(Improved FP-Growth)[9]、FPL/TPL(Frequent Pattern List/Transcation Pattern List)[10]等，上述兩類算法都是基于水平數據格式的。第三類算法是基于垂直數據格式的,如Eclat(Equivalence Class Transformation)以及使用位向量優化的類Eclat算法等。

所有的FIM算法都包含兩個基本計算步驟:產生(候選)項集及對項集進行計數。“產生-計數”類的方法在項枚舉樹上通過廣度優先搜索(Breadth First Search, BFS)產生候選項集,并通過掃描整個數據集對每一個候選項集進行計數,從而得到頻繁項集。“模式增長”及基于垂直數據格式的算法均通過深度優先搜索(Depth First Search, DFS)產生候選項集,可以盡可能早地將非頻繁的項集進行剪枝,效率比BFS方法更高。“模式增長”方法中項集的計數通過構造條件數據庫來實現,設有前綴項集p,其條件數據庫為Dp(由數據集中所有包含項集p的事務組成),找到Dp中i個頻繁項{x1,x2,…,xi},可以直接得到i個頻繁項集{p∪x1,p∪x2,…,p∪xi}。基于垂直數據格式的FIM算法通過計算兩個項集tidset的交集來確定生成項集的支持度,設有兩個tidset:ta={1,2,3,4},tb={2,3}分別表示項a在事務號為{1,2,3,4}的事務中出現,項b在事務號為{2,3}的事務中出現,則tab=ta∩tb={2,3},項集{a,b}的支持度即為tab的長度。可以將項集的tidset轉換為bitmap來進一步提高計算交集的速度[11]。

被挖掘數據集的特征對FIM算法的效率有著顯著影響。數據集的特征主要包括事務數、項數、平均事務長度、數據尺寸等,有不少研究都關注了不同FIM算法針對上述特征的擴展性[12]。但上述屬性只能反映了數據集的一般特征,沒有從根本上描述數據集的本質特征。數據集的稀疏度描述的是數據集中事務之間的差異度及信息的冗余量,是數據集的本質特征之一,對FIM算法的效率有著顯著的影響,很少研究關注了FIM算法對于稀疏度的可擴展性問題。

為了了解不同FIM算法對于稀疏度的可擴展性,首先要對數據集稀疏度進行定量的分析。不少研究以數據集的一般特征為基礎,文獻[13-17]中提出了一些數據集稀疏度的度量方法;閆珍等[18]提出一種將事務數據庫轉換為二進制矩陣,借用工程數學中”稀疏矩陣”的概念來描述數據集的稀疏度;還有一些方法首先將數據集轉換為特殊的數據格式(一般為類似FP-Tree的樹結構),通過對特定數據結構的分析來得出數據集的稀疏度[19-20];Shepard[21]在2013年給出了一種基于等價類及等價類內部冗余度的數據稀疏度度量方法。雖然上述稀疏度度量方法一定程度上解決了數據集稀疏度度量問題,但沒有兼顧到FIM任務背景下決定稀疏度的所有要素,且沒有研究關注數據稀疏度對不同類型FIM算法的效率影響。

本文主要工作為:

1)對已有的數據集稀疏度量化度量方法進行了綜述,討論了每種類型方法的優缺點并進行了比較。

2)提出了一種基于事務頻繁項集之間差異度的數據集稀疏度度量方法,這種度量方法有如下三個特點:考慮了最小支持度對數據稀疏度的影響(不同的支持度會導致頻繁項在數據集中的不同分布),考慮了事務之間的差異(關聯)度,數據集的整體稀疏度由各個局部稀疏度組成。

3)提出了一種基于FP-Tree(Frequent Pattern Tree)的稀疏度的近似度量方法,這種方法同樣考慮了最小支持度以及事務之間部分的差異(關聯)度,雖然是一種近似的稀疏度度量方法,但計算效率比第一種方法更高。

4)通過實驗研究了數據稀疏度對于不同類型FIM算法的性能影響,比較了不同類型FIM算法對數據稀疏度的可擴展性。

1 符號及相關定義

設I={i1,i2,…,in}是項的集合,X是一個項集,X?I,包含k個項的項集稱為k-項集;一個事務T=(tid,X),其中tid為事務標識,X為一個項集;事務數據庫D={t1,t2,…,tn}是T的集合。項集X在事務數據庫D中的支持度Sup(X)為D中包含X事務的數量。最小支持度minsup是用戶給定的一個閾值,如果Sup(x)≥minsup,則稱項集x是頻繁的。

定義1 頻繁項的集合I′。一個事務數據庫D頻繁項的集合由所有頻繁的項組成。

I′={i|i∈I&&Sup(i)≥minsup}

定義2 事務的頻繁項集T′。一個事務T=(tid,X)的頻繁項集T′由事務中所有頻繁的項組成。

T′={i|i∈X&&i∈I′}

定義3 項集的長度|X|。一個項集的長度定義為項集中包含的項的個數。

定義4 設有兩個項集X、Y,其中長度較大的一個項集表示為max(X,Y)。

2 已有度量方法

為了量化度量數據集的稀疏度,已提出的方法可以大致分為三類:第一類是使用數據集的基本特征作為參數來計算數據集的稀疏度;第二類是將數據集轉換為特定的數據結構(大多是類似于FP-Tree的樹結構),通過對特定數據結構特征的分析來體現數據集的稀疏度;第三類是利用等價類(閉項集)的概念,將事務的頻繁項集劃分為若干個等價類,通過計算每一個等價類的稀疏度來得到整個數據集的稀疏度度量。

從FIM挖掘的背景來看,數據集的稀疏度度量方法應考慮三個方面的要素:一是要考慮最小支持度的影響，根據先驗性質[1],FIM挖掘只關注數據集中所有頻繁的項,不同的支持度會導致事務中包含不同的頻繁項;二是要考慮事務頻繁項集之間的差異度,全面地反映一個數據集內事務之間的關聯程度;三是可以將整個數據集劃分為若干部分,整個數據集的稀疏度由所有局部稀疏度構成。

2.1 數據集基本特征的度量方法

Bayardo等[13]提出了一種數據集稀疏度度量的粗略描述,將稀疏數據集描述為“數據集中有大量的項,但每條事務中項的數量(平均事務長度)是很小的。”稀疏度的計算方法如下所示:

數據稀疏度使用事務平均長度和數據集中項總數的比值體現,這種計算方法沒有涵蓋上述三個要素的任何一個,只能說是一種十分粗略的稀疏度定量描述,其優點是計算十分方便。

Gouda等[14]中提出一種利用頻繁項集長度大致估計數據集稀疏度的方法。如果頻繁項集的平均長度很長,則數據是密集的;反之是稀疏的。這種方法只能給出一個粗略的定性描述,且沒有明確頻繁項集的平均長度的閾值是多少。

有不少研究利用頻繁項的平均支持度與最小支持度的比值作為量化估計數據集的方法,其計算公式為:

數據越密集,則密集度越大;數據越稀疏,則密集度越小,稀疏度越大。這種方法雖然考慮了最小支持度對數據稀疏度的影響,計算也十分簡便,但只考慮了數據集中頻繁的項,而沒有考慮事務頻繁項集之間的關聯關系,不能全面反映一個數據集的特征。

文獻[15-17]中提出的度量方法考慮了項在整個數據集中的分布情況,使用分布比例來衡量數據集的稀疏度。設數據集中所有項的集合I={i1,i2,…,in},數據集稀疏度計算方法如下所示:

分布比例越高,則數據集越密集;分布比例越低,則數據集越稀疏。這種方法計算也十分簡單,但存在著明顯的缺點:沒有體現最小支持度對數據集稀疏度的影響;沒有反映事務頻繁項集之間的關聯程度;在某些情況下,兩個數據集可能擁有相同的項分布比例,但兩個數據集實際上存在著重大的差異。

閆珍等[18]提出的方法與分布比例的思想類似,首先將事務數據庫轉換為二進制矩陣,通過矩陣中非零元素的占比來得到數據集的稀疏度,其計算公式如下:

稀疏度=t/(m×n)

其中:t為矩陣中非零元素的個數;m×n為矩陣的尺寸。一般而言,稀疏度小于等于0.05為稀疏數據集[22]。

2.2 基于特殊數據結構的度量方法

Grahne等[19]中提出一種基于FP-Tree的稀疏度粗略的估計方法,首先將數據集構造成一棵FP-Tree,然后以樹層次的方法對該FP-Tree進行檢查:若FP-Tree上1/4部分包含的節點少于15%的總結點,則數據集是密集的；否則數據集是稀疏的。這種方法考慮了最小支持度的影響,也考慮了事務頻繁項集之間的關聯程度,但只能得出定性的稀疏度度量結論(密集或稀疏),無法量化一個數據集的稀疏程度。在文獻[23]中說明,這種度量方法有時會產生錯誤的結論。

為了克服稀疏度不能準確量化度量的缺點,Salleb-Aouissi等[20]提出一種精確的度量方法,首先將數據集構成一個類似FP-Tree的數據結構二元決策圖(Binary Decision Diagram, BDD),通過檢查BDD的特征來得出數據集量化的稀疏度,具體計算公式如下:

若SPBDD的比值很小,說明BDD中的節點很少,數據集是密集的;反之數據集為稀疏的。這種方法可以得到一個精確量化的稀疏度度量,但沒有考慮最小支持度的因素。

上述兩種基于樹的度量方法實際上主要關注點是事務之間的差異(關聯)程度。如果事務之間的差異度低,則在FP-Tree或BDD中一個節點可以代表多個事務共同項,整個數據結構中的節點就相應減少;反之則BDD中的節點數量更多。

2.3 基于等價類劃分的度量方法

Shepard[21]中提出一種基于等價類的數據集稀疏度度量方法,主要借助了閉項集及等價類中的最小項集(Mininal Generators, MG)的概念[24]。其計算方法主要描述為:首先將數據集的所有事務劃分為n個等價類{Y1,Y2,…,Yn},同一等價類中的事務具有相同的閉項集,整個數據集的稀疏度是所有等價類稀疏度的平均數:

每一個等價類稀疏度的計算方法為:

Sp(Yi)=y/x2

其中:y為等價類中無冗余的mg的個數;x為等價類中所有的項集數。

這種度量方法雖然可以給出一個量化精確的稀疏度度量,也考慮了部分事務之間的關聯(同一個等價類內部的事務),但很明顯,它沒有考慮最小支持度對數據集稀疏度的影響,且沒有考慮不同等價類之間的關聯關系。

可以將上述度量方法從三個維度對比如表1所示。

表1 六類稀疏度度量方法的比較

3 稀疏度度量方法

本文首先提出一種定量的稀疏度度量方法,考慮最小支持度對數據集稀疏度的影響,全面關注事務之間的差異度(關聯程度),整個數據集的稀疏度由局部稀疏度組成。

3.1 基于事務差異度的稀疏度度量方法

由于不同最小支持度下事務的頻繁項集是完全不同的,因此在FIM任務背景下,數據集的稀疏度是一個與最小支持度緊密關聯的指標。設數據集D={T1,T2,…,Tn},則所有事務之間的關系可用R來表示:

R={r|r=(Ti,Tj)}; 1≤i≤n, 1≤j≤n,i≠j

在FIM任務背景下,只需要考慮事務頻繁項集之間的關系,可以得到R′:

R′={r′|r′= (Ti′,Tj′)}; 1≤i≤n, 1≤j≤n,i≠j

其中：Ti′為Ti的頻繁項集。

整個數據集的稀疏度可由任意兩個事務之間的差異度定義而來。可以對任意事務之間的差異度求平均數得到數據集的稀疏度,即如下定義:

定義5 設數據集D中共有n條事務,其關系集合R′={r1,r2,…,rn},數據集D的稀疏度定義為SP(D),計算公式為:

下面討論任意兩個事務頻繁項集之間差異度的計算問題。本文引入數據挖掘領域中“標稱屬性”的概念[25],將一個事務看成是由若干個標稱屬性刻畫的對象,其頻繁項集中的每一個項可以看成是一個標稱屬性。如有兩個事務的頻繁項集X′={a,b,c}和Y′={b,c,d,e},則事務X′有3個標稱屬性,Y′有4個標稱屬性。計算兩個使用標稱屬性刻畫的實體i、j之間差異度dif(i,j)可使用如下計算公式[25]:

dif(i,j)= (p-m)/p

其中:m為i、j中相同的屬性數;p為刻畫實體屬性的總數。如將X′和Y′均看成使用標稱屬性刻畫的實體,它們具有共同的標稱屬性{b,c},刻畫實體所有的屬性數為4,則兩者的差異度為(4-2)/4=0.5。

因此,可以正式將兩個事務的頻繁項集之間的差異度定義如下:

定義6 兩個事務的頻繁項集Ti′和Tj′之間的差異度定義為dif(Ti′,Tj′),其計算方法為:

dif(Ti′,Tj′)=

下面討論數據集稀疏度的最大值和最小值。根據定義5,Sp(D)由任意兩條事務的頻繁項集之間的差異度求平均值所得。對于dif(Ti′,Tj′),若Ti′和Tj′的長度相等且每一個項均相等,則dif(Ti′,Tj′)=0;若Ti′和Tj′的長度相等且每一個項均不相等,則dif(Ti′,Tj′)=1;除了上述兩種極端情況之外,dif(Ti′,Tj′)是一個在范圍(0,1)內的小數。因此對于SP(D)而言,其取值必然在區間[0,1]內。為了便于查看和書寫,可以將SP(D)×100%得到的一個百分比作為數據集稀疏度的表現方式。

3.2 基于FP-Tree的稀疏度度量方法

3.1節提出的稀疏度度量方法支持最小支持度考慮了所有事務之間的差異度,具有較好的代表性;但有一個明顯的缺陷,即計算成本很高。設數據集D中有n個事務,則R′中有[n(n-1)]/2個元素,計算一個關系差異度的時間復雜度為O(1),則計算SP(D)的時間復雜度為O(n2),當數據集中包含海量事務時,計算成本很高。為了降低計算成本,可以將基于FP-Tree的方法和計算SPBDD的方法進行結合,提出一種新的基于FP-Tree的稀疏度計算方法。其主要思想是將數據集轉換為對應的FP-Tree后,對FP-Tree中的節點進行檢查來代表數據集的稀疏度。設數據集D的I′={i1,i2,…,in},基于FP-Tree的稀疏度計算方式如下:

這種計算方法在構造FP-Tree時支持最小支持度,通過FP-Tree的節點共享體現事務之間的差異度。設數據集中有n個事務,若任意兩個事務的頻繁項集Ti′和Tj′的長度相等且每一個項均相等,則數據集最密集,FPSP(D)=1/n;若任意兩個事務的頻繁項集Ti′和Tj′的長度相等且每一個項均不相等,則數據集最稀疏,FPSP(D)=1;因此對于任何數據集D,FPSP(D)的取值范圍為[1/n, 1]。

4 實驗結果分析

實驗選取FIM挖掘標準數據集[26]中的四個數據集用于測試本文提出的兩種稀疏度計算方法及三種典型FIM算法對于稀疏度的可擴展性。其中：mushroom和chess為兩個傳統的密集數據集,retail和T10I4D100K為兩個傳統的稀疏數據集。數據集的基本屬性如表2所示。

表2 四個測試數據集的基本屬性

4.1 稀疏度度量結果對比

使用本文第3章中提出的兩種稀疏度量化度量方法,對四個標準數據集分別計算其量化稀疏度,第一種方法度量值記為SP,第二種方法度量值記為FPSP。具體結果見圖1。

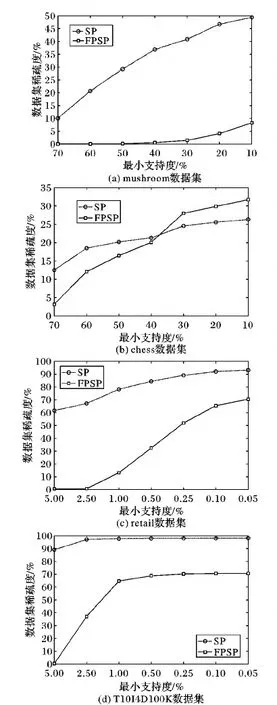
圖1 本文提出的兩種方法對四個標準數據集的度量結果

從圖1可以看出:

1)在FIM任務背景下,數據集稀疏度(SP)是一個與最小支持度(minsup)相關聯的一個數值,且與最小支持度成反比。

2)本文提出的兩種稀疏度度量方法都具有良好的區分度,即對于一個數據集而言,不存在支持度不同而稀疏度相同的情況。從文獻[21]中可以看出,基于等價類的稀疏度度量方法在T40I0D100K數據集上,當最小支持度分別為1%、1.5%、2%、2.5%、5%、10%時,其稀疏度值均為100%,基于等價類的稀疏度度量方法在某些數據集上區分度較差。

3)對于相對密集的數據集來說,如mushroom和chess,SP的數值與minsup成近似線性關系,而FPSP增長得比較慢(主要原因是事務的頻繁項集之間差別較小,可以共享很多前綴);而對于較為稀疏的數據集來說,如retail和T10I4D100K,SP的增長率較小,而FPSP的增長率較大,這也說明對于稀疏度很高的數據集,不適合使用基于FP-Tree的FIM算法(如FP-Growth),會構造大量的條件數據庫，影響算法效率。

將文獻[17,21]中提出的稀疏度計算方法分別記為SPmg和CD,選擇標準數據集中較為密集的數據集mushroom和稀疏數據集T10I4D100K,分別計算四種稀疏度如表3所示。

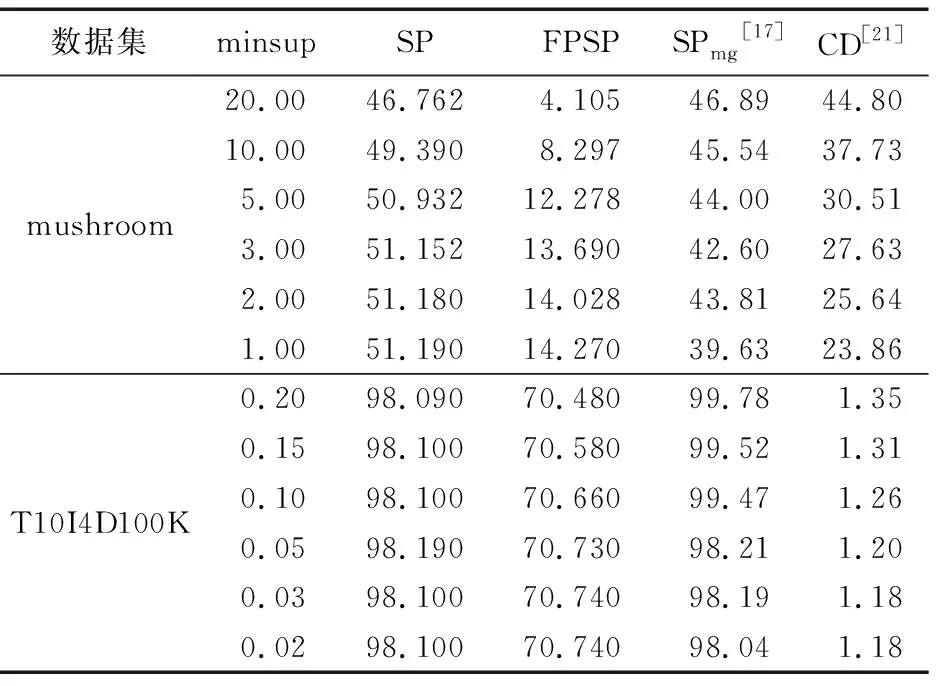
表3 不同度量方法在兩個數據集上的比較 %

從表3可以看到,本文提出的度量方法與已有方法在度量值上具有一定的一致性。但本文提出的兩種度量方法均以事務之間的差異性為基礎,度量值與最小支持度之間成明顯的反比關系,而SPmg以等價類中的冗余度為基礎,CD主要考慮的是項在數據集中的分布情況,相對來說其度量值和最小支持度之間的關聯性不明顯。

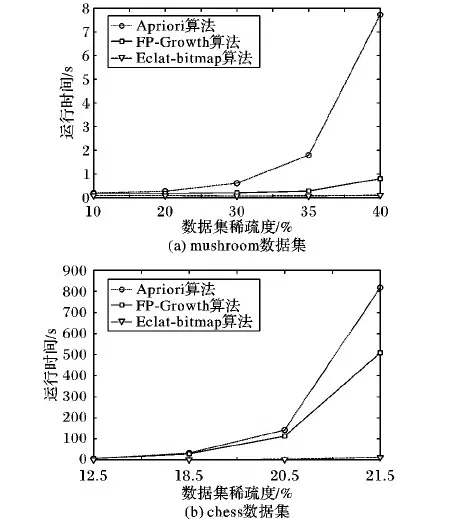
圖2 三種算法在密集據集上的執行時間

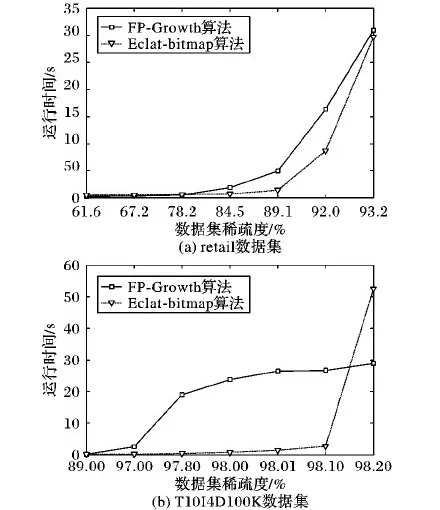
圖3 兩種算法在稀疏數據集上的執行時間

4.2 三種類型算法效率對比

從三類FIM算法中各選取一種經典的算法,研究其對于數據稀疏度的擴展性。“產生-測試”類選擇經典的Apriori算法;“模式增長”類選擇經典的FP-Growth算法;基于垂直數據格式的算法選擇基于bitmap優化的Eclat算法(Eclat-bitmap算法)。

三種算法在兩個較密集的數據集上執行時間如圖2所示,從中可以看出:

1)Apriori算法的性能隨著數據集稀疏度的增長降低得十分明顯。其主要原因是隨著稀疏度的增長,數據集中頻繁項的數量急劇增長,基于BFS的候選項集產生策略會導致候選項集數量相對于頻繁項的數量呈指數級別增長,極大地影響Apriori算法的性能。

2)FP-Growth算法的性能在數據集稀疏度較小的情況下具有較好的性能,但隨著數據集稀疏度的增加會產生明顯的惡化。其主要原因是隨著稀疏度的增長,事務頻繁項集之間的差異度越來越大,導致構造的FP-Tree中事務間共享的節點數量減少,在挖掘過程中構造的條件數據庫數量急劇增加,影響了FP-Growth算法的性能。

3)Eclat-bitmap算法在數據集稀疏度較低的情況下具備十分良好的性能,在候選項集產生及計數兩個階段都優于上述兩種算法。

由于Apriori算法在數據集稀疏度高時性能惡化十分劇烈,因此對于兩個較為稀疏的算法已不再將Apriori算法作為參照對象,只考慮FP-Growth和Eclat-bitmap兩種類型的算法。

FP-Growth算法和Eclat-bitmap算法在兩個較稀疏的數據集上執行時間如圖3所示，從中可以看出:

1)相比較而言,Eclat-bitmap算法在稀疏度較低的情況下,性能比FP-Grwoth算法要出色。但當稀疏度上升到一定高度時,性能與FP-Growth相當。

2)在稀疏度極高時,已有的三種典型算法的性能都不能令人十分滿意,不能很好地解決極度稀疏數據集中的FIM問題。

5 結語

數據集的特征對FIM算法的性能有著顯著的影響,除了事務數、項數及平均事務長度等數據集的一般特征外,稀疏度是描述數據集本質特征最重要的屬性之一。本文提出了兩種量化度量數據集稀疏度的方法,考慮了最小支持度對數據集稀疏度的影響和事務之間的差異性:基于事務差異度的度量方法全面反映了所有事務之間的差異性(關聯性);而基于FP-Tree的度量方法具有更好的計算性能。從實驗結果來看,三種類型算法中“產生-測試”類的方法(如Apriori)對稀疏度擴展性最差,基于數據垂直格式的方法(如Eclat-bitmap)對稀疏度的擴展性最好,但當數據稀疏度增大到一定程度時,性能仍然出現了極度的惡化。因此,對于極度稀疏的數據集,可以數據垂直格式方法的設計思路,優化設計新的FIM算法,來提高挖掘的效率。

參考文獻(References)

[1] AGRAWAL R, IMIELINSKI T, SWAMI A N. Mining association rules between sets of items in large databases[C]// Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data. New York: ACM,1993: 207-216.

[2] AGRAWAL R, SRIKANT R. Fast algorithms for mining association rules in large databases[EB/OL]. [2017- 05- 10]. http://www.cs.uu.nl/docs/vakken/adm/agrawalfast.pdf.

[3] PARK J S, CHEN M S, YU P S. Using a hash-based method with transaction trimming for mining association rules[J]. IEEE Transactions on Knowledge & Data Engineering, 1997, 9(5): 813-825.

[4] OZEL S A, GUVENIR H A. An algorithm for mining association rules using perfect hashing and database pruning[C]// Proceedings of the 10th Turkish Symposium on Artificial Intelligence and Neural Networks. Berlin: Springer, 2001: 257-264.

[5] BRIN S, MOTWANI R, ULLMAN J D, et al. Dynamic itemset counting and implication rules for market basket data[J]. ACM Sigmod Record, 2001, 26(2): 255-264.

[6] HAN J, PEI J, YIN Y, et al. Mining frequent patterns without candidate generation: a frequent-pattern tree approach[J]. Data Mining & Knowledge Discovery, 2015, 8(1): 53-87.

[7] PYUN G, YUN U, RYU K H. Efficient frequent pattern mining based on linear prefix tree[J]. Knowledge-Based Systems, 2014, 55: 125-139.

[8] TSAY Y J, HSU T J, YU J R. FIUT: a new method for mining frequent itemsets[J]. Information Sciences, 2009, 179(11): 1724-1737.

[9] LIN K C, LIAO I E, CHEN Z S. An improved frequent pattern growth method for mining association rules[J]. Expert Systems with Applications, 2011, 38(5): 5154-5161.

[10] TSENG F C. An adaptive approach to mining frequent itemsets efficiently[J]. Expert Systems with Applications, 2012, 39(18): 13166-13172.

[11] BURDICK D, CALIMLIM M, FLANNICK J, et al. MAFIA: a maximal frequent itemset algorithm[J]. IEEE Transactions on Knowledge & Data Engineering, 2005, 17(11): 1490-1504.

[12] GOETHALS B, ZAKI M J. Advances in frequent itemset mining implementations: report on FIMI’03[J]. ACM Sigkdd Explorations Newsletter, 2003, 6(1): 109-117.

[13] BAYARDO R J J, AGRAWAL R, GUNOPULOS D. Constraint-based rule mining in large, dense databases[J]. Data Mining & Knowledge Discovery, 2000, 4(2/3): 217-240.

[14] GOUDA K, ZAKI M J. Efficiently mining maximal frequent itemsets[C]// ICDM 2001: Proceedings of the 2001 IEEE International Conference on Data Mining. Washington, DC: IEEE Computer Society, 2001: 163-170.

[15] PALMERINI P, ORLANDO S, PEREGO R. Statistical properties of transactional databases[C]// SAC 2004: Proceedings of the 2004 ACM Symposium on Applied Computing. New York: ACM, 515-519.

[16] STEINBACH M, TAN P N, KUMAR V. Support envelopes: a technique for exploring the structure of association patterns[C]// Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2004: 296-305.

[17] YAN H, CHEN K, LIU L, et al. SCALE: a scalable framework for efficiently clustering transactional data[J]. Data Mining & Knowledge Discovery, 2010, 20(1): 1-27.

[18] 閆珍, 皮德常, 吳文昊. 高維稀疏數據頻繁項集挖掘算法的研究[J]. 計算機科學, 2011, 38(6): 183-186.(YAN Z, PI D C, WU W H. Research on frequent itemsets mining algorithm for high-dimensional sparse data[J]. Computer Science, 2011, 38(6): 183-186.)

[19] GRAHNE G, ZHU J F. Efficiently using prefix-trees in mining frequent itemsets[EB/OL]. [2017- 05- 10]. http://ceur-ws.org/Vol-90/grahne.pdf.

[20] SALLEB-AOUISSI A, VRAIN C. A Contribution to the Use of Decision Diagrams for Loading and Mining Transaction Databases[M]. Amsterdam: IOS Press, 2007:220-242.

[21] SHEPARD T H. Looking for a structural characterization of the sparseness measure of(frequent closed) itemset contexts[J]. Information Sciences, 2013, 222(3): 343-361.

[22] 嚴蔚敏, 吳偉民. 數據結構(C語言版) [M]. 北京:清華大學出版社, 2007: 96-96.(YAN W M, WU W M. Data Structure(C Language Edition) [M]. Beijing: Tsinghua University Press, 2007: 96-96.)

[23] YAHIA S B, HAMROUNI T, NGUIFO E M. Frequent closed itemset based algorithms[J]. ACM SIGKDD Explorations Newsletter, 2006, 8(1): 93-104.

[24] PASQUIER N, BASTIDE Y, TAOUIL R, et al. Discovering frequent closed itemsets for association rules[C]// ICDT 1999: Proceedings of the 7th International Conference on Database Theory, LNCS 1540. Berlin: Springer, 1999: 398-416.

[25] 韓家煒, 范明.數據挖掘: 概念與技術[M]. 北京:機械工業出版社, 2012: 27-46.(HAN J W, FAN M. Data Mining: Concepts and Techniques[M]. Beijing: China Machine Press, 2012: 27-46.)

[26] IEEE computer society. Frequent itemset mining dataset repository[DB/OL].[2017- 11- 01].http://fimi.ua.ac.be/data/.

This work is partially supported by the Natural Science Foundation of the Colleges and Universities in Anhui Province (KJ2016A623).