馬爾科夫跳變系統(tǒng)的不定平均場隨機線性二次最優(yōu)控制問題

,,(山東科技大學 數(shù)學與系統(tǒng)科學學院，山東 青島 266590)

近幾十年來，馬爾科夫跳變系統(tǒng)獲得極大關(guān)注，并被應用于各個領(lǐng)域，例如航天器設計、太陽能站、衛(wèi)星動態(tài)系統(tǒng)、證券投資組合最優(yōu)化以及通訊網(wǎng)絡等。文獻[1]中有很多關(guān)于離散時間馬爾科夫跳變系統(tǒng)的基礎知識，文獻[2]則講解關(guān)于最優(yōu)控制的基本問題和應用。文獻[3]是隨機奇異系統(tǒng)的線性二次帕累托最優(yōu)控制問題，文獻[4]研究隨機的離散時間線性二次最優(yōu)控制問題，文獻[5]和[6]分別研究離散時間平均場線性二次最優(yōu)控制問題對于有限和無限時間的情況。

最優(yōu)控制理論由經(jīng)典變分學發(fā)展起來，其歷史可追溯到360年前。但是直到上世紀60年代，人們才真正對其產(chǎn)生興趣[7]。文獻[8]利用一種非協(xié)調(diào)有限元局部穩(wěn)定化方法解決Navier-Stokes方程的最優(yōu)化問題。動力學系統(tǒng)的數(shù)學模型為線性方程,所取的性能指標為狀態(tài)變量與控制變量的二次型函數(shù),這種動態(tài)系統(tǒng)的最優(yōu)化問題稱為線性二次型(linear quadratic, LQ)問題。由于LQ問題的最優(yōu)解具有統(tǒng)一的解析表達式,且可得到一個線性的狀態(tài)反饋控制律,便于計算和實現(xiàn)閉環(huán)反饋控制,從而成為最優(yōu)控制理論及應用中最成熟的部分[9]。文獻[10]研究一類含消費、壽險和投資的隨機最優(yōu)控制問題。

馬爾科夫跳系統(tǒng)作為一類典型的混雜動態(tài)系統(tǒng)，由于其強大的建模能力在各個領(lǐng)域已經(jīng)得到廣泛的應用[11]。文獻[12]研究帶有馬爾科夫跳變參數(shù)的連續(xù)時間線性二次問題。文獻[13]討論連續(xù)時間馬爾科夫跳變系統(tǒng)的時變問題，通過一個帶有馬爾科夫跳變的性能指標來解決不定線性二次最優(yōu)控制問題，并研究了代替平均差的標準。

本文研究一類離散時間平均場隨機線性二次最優(yōu)控制問題。平均場能夠簡化對復雜問題的研究，把一個高次、多維的難以求解的問題轉(zhuǎn)化為一個低維問題。近來，平均場類型的隨機最大值原理獲得廣泛關(guān)注，文獻[14]研究局部信息下平均場類型最優(yōu)控制問題的隨機最大值原理。文獻[15]在傳統(tǒng)傳染病SIR模型的基礎上，利用平均場改進為一個基于用戶影響力的信息傳播模型。文獻[16]通過變分法，推導出平均場類型的隨機最大值原理的最優(yōu)化系統(tǒng)是一個線性平均場前后隨機差分方程。

文獻[17]針對跳變系統(tǒng)參數(shù)矩陣不確定的情況，引進一種新的分解技術(shù)，將不同時刻下的系統(tǒng)綜合考慮，以矩陣塊的方式給出最優(yōu)控制的表達式。與文獻[17]相比較，本研究將系統(tǒng)和性能指標的加權(quán)矩陣推廣到不定的情況，首先定義一個差分黎卡提方程，并得到最優(yōu)控制存在的充分條件是黎卡提方程可解，給出最優(yōu)控制的一般表達式以及不考慮平均場時的特殊形式，可視為對文獻[17]結(jié)果的一個推廣。

1 問題闡述與定義準備

研究如下帶有乘性噪音的系統(tǒng)：

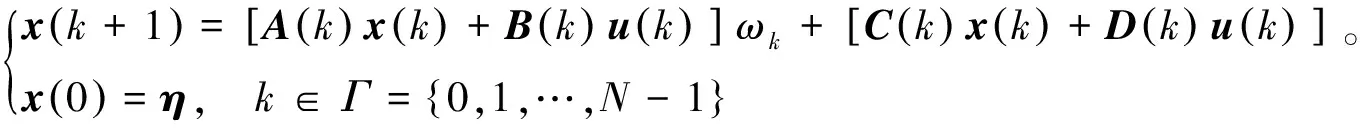
(1)

其中：A，C∈Rn×n和B，D∈Rn×m都是對稱矩陣，x(k)和u(k)分別是狀態(tài)變量和控制變量。噪聲擾動參數(shù)ω≡{ωk}以及狀態(tài)初始值η均定義在完備概率空間(Ω,F,P)上。狀態(tài)初始值η是0時刻的狀態(tài)值，即η=x(0)。噪聲擾動參數(shù)ω是一個有限二階矩的鞅差分序列，并且E[ωk+1|Fk]=0，其中Fk是由集合{x(0),ωl,θl,l=0,1,…,k}所產(chǎn)生的σ-代數(shù)，并且滿足:

(2)

考慮下面的性能標準:

J(x(0),u(k),θ0)

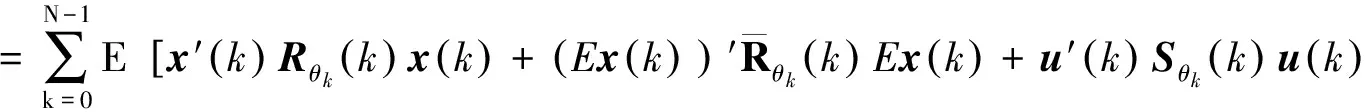
(3)

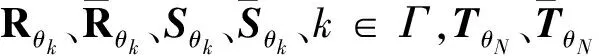
pij=P(θk+1=j|θk=i),i,j∈M,k∈Γ。

(4)

E是期望算子，對于k=0,1,…,N，記：

定義1.1(MF-LQ) 對于任意的初始值η，如果存在u0(k)∈U使得:

(5)

其中，U是可容許控制集，則稱u0(k)是MF-LQ問題的最優(yōu)控制。

本研究系統(tǒng)和性能指標的加權(quán)矩陣可以是不定的，為方便后續(xù)使用，引入廣義逆矩陣的定義。

定義1.2[18]給定矩陣Q∈Rm×n，則存在一個唯一的矩陣Q+∈Rn×m，稱為Q的廣義逆矩陣，使得:

(6)

引理1.3[18]給定對稱矩陣L，M，N，則矩陣方程LXM=N有解X的充要條件是:

LL+NMM+=N，

并且解的一般表達式為X=L+NM++Y-L+LYMM+，其中Y是合適維數(shù)的任意矩陣。

2 主要結(jié)果

為定義系統(tǒng)(1)的廣義黎卡提差分方程，先引入兩個等式

E[x′(N)PθN(N)x(N)]-E[x′(0)Pθ0(0)x(0)]

(7)

以及

(8)

通過噪聲擾動參數(shù)的性質(zhì)以及簡單的計算有：

E[x′(k+1)Pθk(k+1)x(k+1)|Fk]

=x′(k)[A′(k)E(Pθk(k+1))A(k)+C′(k)E(Pθk(k+1))C(k)]x(k)

+2x′(k) [A′(k)E(Pθk(k+1))B′(k) +C′(k)E(Pθk(k+1))C′(k)]u(k)

+u′(k)[B′(k)E(Pθk(k+1))B′(k)+D′(k)E(Pθk(k+1))D′(k)]x(k),

(9)

故有:

E[x′(N)PθN(N)x(N)]-E[x′(0)Pθ0(0)x(0)]

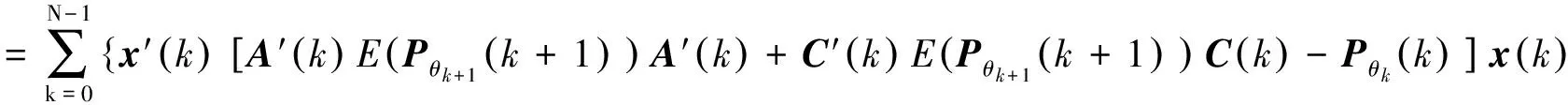
+2x′(k)[A′(k)E(Pθk+1(k+1))B(k)+C′(k)E(Pθk+1(k+1))D(k)]u(k)

+u′(k)[B′(k)E(Pθk+1(k+1))B(k)+D′(k)E(Pθk+1(k+1))D(k)]u(k)},

(10)

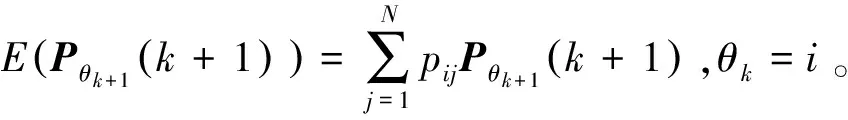
(11)

通過式(3)以及式(7)、(8)、(10)、(11)，有：

J(x(0),u(k),θ0)

-Pθk(k)]x(k)+2x′(k) [A′(k)E(Pθk+1(k+1))B(k)+C′(k)E(Pθk+1(k+1))D(k)]u(k)

+u′(k) [Sθk(k)+B′(k)E(Pθk+1(k+1))B(k) +D′(k)E(Pθk+1(k+1))D(k)]u(k)

(12)

定義2.1給出下面的約束差分方程：

(13)

其中

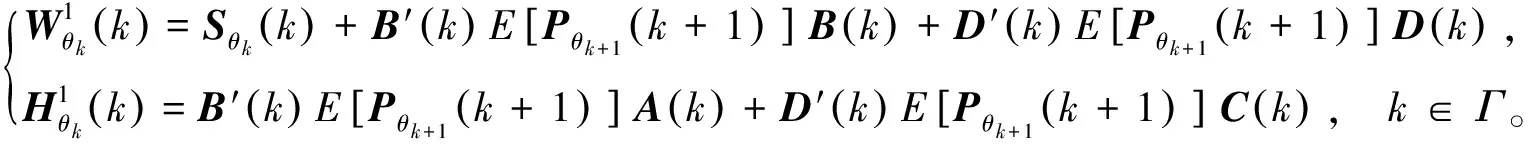
(14)

和

(15)

其中

(16)

稱為乘性噪聲系統(tǒng)的廣義差分黎卡提方程。

定理2.2對于線性二次最優(yōu)化問題(1)、(3)、(5)，最優(yōu)控制:

(17)

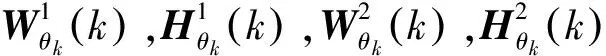
(18)

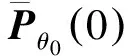
證明：通過簡單的完全平方計算以及定義2.1，(12)式可以轉(zhuǎn)化為:

J(x(0),u(k),θ0)

×E(Pθk + 1(k+ 1))C(k)](x(k)-Ex(k))+ 2(x(k)-Ex(k))[A′(k)

×E(Pθk + 1(k+ 1))B(k) +C′(k)E(Pθk + 1(k+ 1))D(k)](u(k)-Eu(k))

+ (u(k)-Eu(k))[Sθk(k) +B′(k)E(Pθk + 1(k+ 1))B(k) +D′(k)

+A′(k)E(Pθk + 1(k+ 1))A(k)]Ex(k) + (Ex(k))[C′(k)(E(Pθk + 1(k+ 1))

+E(x′(0)Pθ0(0)x(0))

(19)

令

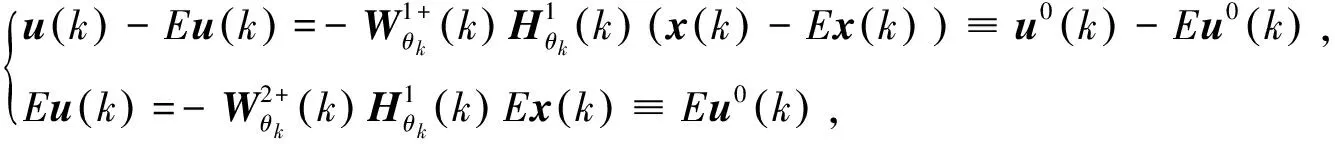
(20)

求解方程組(20)，得最優(yōu)控制的表達式為:

(21)

相應的性能指標的最小值：

(22)

證明結(jié)束。

注釋2.3特別地，當系統(tǒng)(1)、(4)、(5)中加權(quán)矩陣正定時，并且系統(tǒng)中不再考慮跳變參數(shù)時，定理2.2變?yōu)槲墨I[23]定理3.1。

推論2.4當性能指標中不考慮平均場，對應的最優(yōu)控制為:

(23)

相應性能指標最小值:

(24)

證明：通過定義2.1 和簡單的完全平方計算，(12)式可以轉(zhuǎn)換為:

J(x(0),u(k),θ0)

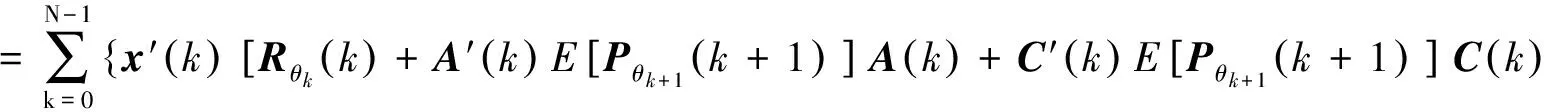
-Pθk(k)]x(k)+2x′(k) [A′(k)E[Pθk+1(k+1)]B(k)+C′(k)E[Pθk+1(k+1)]D(k)]u(k)

+u′(k) [Sθk(k)+B′(k)E[Pθk+1(k+1)]B(k)+D′(k)E[Pθk+1(k+1)]D(k)]u(k)}

+E[x′(0)Pθ0(0)x(0)]

+E[x′(0)Pθ0(0)x(0)],

(25)

則最優(yōu)控制為:

(26)

相應性能指標最小值:

(27)

證明結(jié)束。

3 數(shù)值例子

這一部分研究一個數(shù)值例子。對于給定的系統(tǒng):

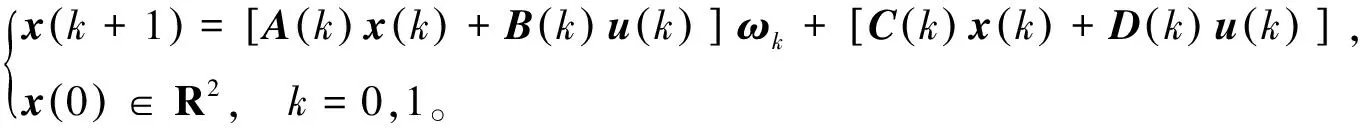
考慮下面的性能指標:

其中，馬爾科夫鏈θ的取值為1，2，轉(zhuǎn)移概率矩陣為:

其中

pij=p(θk+1=j|θk=i),i,j=1,2,k=0,1,2。

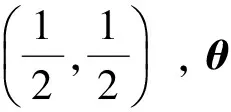
對于任意的k=0,1，2，當θk=1時，

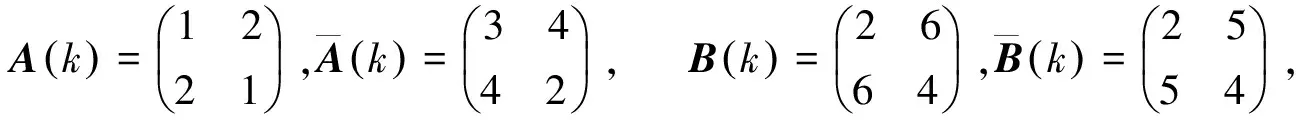
對于任意的k=0,1,2，當θk=2時，

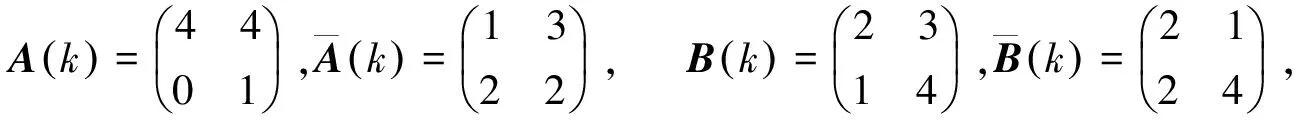
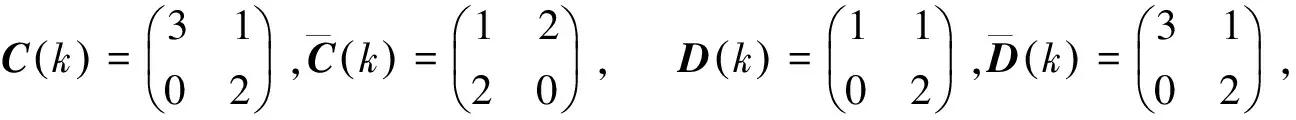
通過式(13)～(16)，對于任意的k=0,1,2，當θk=1時，有:

最優(yōu)控制(17)式中的對應系數(shù)如下:

當對于任意的k=0,1,2，當θk=2時，有:

最優(yōu)控制(17)式中的對應系數(shù)如下:

則最優(yōu)控制和性能指標的表達式如下:

以及

和

令x(0)=(0,1)′，則

4 總結(jié)

研究了乘性噪聲系統(tǒng)的不定平均場隨機線性二次最優(yōu)控制問題，系統(tǒng)和性能指標中的參數(shù)矩陣允許是不定的，首先定義一種廣義差分黎卡提差分方程，證明其可解性是最優(yōu)控制存在的充分條件。其次，推導出最優(yōu)控制的一般表達式。最后，給出沒有平均場時最優(yōu)控制的特殊形式。

參考文獻：

[1]COSTA O L V,FRAGOSO M D,MARQUES R P.Discrete-time Markov jump linear systems[M].London：Springer-Verlar,2005:916-917.

[2]解學書.最優(yōu)控制理論與應用[M].北京:清華大學出版社,1986.

[3]ZHANG W H,LIN Y N,XUE L G.Linear quadratic Pareto optimal control problem of stochastic singular systems[J].Journal of the Franklin Institute,2017,354(2):1220-1238.

[4]LIU X K,LI Y,ZHANG W H.Stochastic linear quadratic optimal control with constraint for discrete-time systems[J].Applied Mathematics and Computation,2014,228:264-270.

[5]ELLIOTT R,LI X,NI Y H.Discrete time mean-field stochastic linear-quadratic optimal control problem[J].Automatica,2013,49:3222-3233.

[6]NI Y H,ELLIOTT R,LI X.Discrete time mean-field stochastic linear-quadratic optimal control problem,II:Infinite horizon case[J].Automatica,2015,57:65-77.

[7]韋蘭用.最優(yōu)控制問題研究綜述[D].長春:吉林大學,2006.

[8]覃艷梅,李輝,馮民富.Navier-Stokes方程最優(yōu)控制問題的一種非協(xié)調(diào)有限元局部穩(wěn)定化方法[J].應用數(shù)學和力學,2016,37(8):842-855.

QIN Yanmei,LI Hui,FENG Mingfu.A local stabilization nonconforming finite element method for the optimal control of Navier-Stokes equations[J].Applied Mathematics and Mechanics,2016,37(8):842-855.

[9]馬宏基.不定隨機線性二次最優(yōu)控制若干問題的研究[D].青島:山東科技大學,2007.

[10]梁宗霞,趙笑陽.一類含消費、壽險和投資的隨機最優(yōu)控制問題[J].中國科學,2016,46(12)：1863-1882.

LIANG Zongxia,ZHAO Xiaoyang.Optimal investment,consumption and life insurance under stochastic framework[J].Science China,2016,46(12):1863-1882.

[11]李繁飆.半馬爾科夫跳變系統(tǒng)的分析和綜合[D].哈爾濱:哈爾濱工業(yè)大學,2015.

[12]ZHOU J.On stochastic Riccati equations for the stochastic LQR problem[J].Systems & Control Letters,2005,54(2):119-124.

[13]DRAGAN V,MOROZAN T.The linear quadratic optimization problems for a class of linear stochastic systems with multiplicative white noise and Markovian jumping[J].IEEE Transactions on Automatic Control,2004,49(5):665-675.

[14]WANG G C,ZHANG C H,ZHANG W H.Stochastic maximum principle for mean-field type optimal control under partial information[J].IEEE Transactions on Automatic Control,2014,59(2):522-528.

[15]肖云鵬,李松陽,劉宴兵.一種基于社交影響力和平均場理論的信息傳播動力學模型[J].物理學報,2017,66(3):1-13.

XIAO Yunpeng,LI Songyang,LIU Yanbing.An information diffusion dynamic model based on social influence and mean-filed theory[J].Acta Physica Sinica,2017,66(3):1-13.

[16]YONG J M.A linear quadratic optimal control problem for mean-field stochastic differential equations[J].SIAM Journal on Control Optimization,2013,51(4):2809-2838.

[17]NI Y H,LI X,ZHANG J F.Mean-field stochastic linear-quadratic optimal control with Markov jump parameters[J].Systems & Control Letters,2016,93:69-76.

[18]RAMI M A,CHEN X,ZHOU X Y.Discrete-time indefinite LQ control with state and control dependent noises[J].Journal of Global Optimization,2002,23:245-265.