(001)面雙軸應變鍺材料的能帶調控

，， ，，，(.， 508； .工程學院軟件學院， 508； .， 6005)

1 前 言

隨著半導體行業的快速發展，半導體器件特征尺寸將不斷減小，逐漸達到物理和技術上的雙重極限，集成電路的集成度將很難再按照摩爾定律的規律向前發展。因此，我們需要研究開發新的材料、新的器件結構、新的生產工藝以滿足高速處理信息能力的需求[1]。一方面，由于Ge材料的電子和空穴的遷移率均比Si高，科學家們提出利用Ge材料作為MOSFET(Metal-Oxide-Semiconductor Field-Effect-Transistor)的溝道材料以進一步提高微電子器件的性能[2]；另一方面，人們發現，Ge材料具有準直接帶特性[3]，通過張應變、摻雜等能帶改性攻略可以將它調控為準直接帶隙半導體，因此在光電子材料與器件的開發方面，Ge材料具有潛在的應用價值；同時，Ge與傳統的Si工藝兼容性好，在工業生產方面具有價格優勢。

近年來，國內外許多研究機構試圖利用Ge材料的準直接帶特性開發相應的器件用于硅基光電集成，并在實驗方面對(001)面雙軸應變Ge材料與器件的制備技術進行了大量的報道。例如，利用Ge與Si、SiGe、GeSn等晶格失配和熱失配的原理[4-6]，在外延Ge材料時引入一定量的雙軸應變，進而改善材料的光電特性；在新器件開發方向，主要集中于報道雙軸張應變Ge材料在發光及探測方面的潛在應用[7-9]；并且美國MIT研究小組[10](2012年首次報道)和德國Roman Koerner等研究人員[11](2015年報道)先后報道了Si基雙軸張應變Ge室溫電泵激光器，證實了雙軸張應變Ge材料作為激光器增益介質的可靠性。然而，目前制備得到的激光器存在著閾值電流過高，器件工作不穩定等缺點，有待進一步從理論研究、材料生長和器件結構設計等方面進行優化設計。

在理論計算方面，國內外對應變Ge材料的報道主要可以分為兩個方面，一是采用k.p理論計算單軸應變Ge材料的價帶結構[12-13]，二是采用第一性原理或基于實驗參數與經驗公式的理論方法等計算張應變Ge材料的能帶結構[14-18]，并預測Ge材料轉變為直接帶半導體所需要施加的張應變值。Ge半導體的禁帶寬度與應變之間的關系對材料設計、器件模擬等方面具有重要的理論參考價值，目前在這方面報道較少。本文基于形變勢理論詳細對(001)面雙軸應變Ge材料的能帶結構進行理論計算。首先分析了應變對Ge晶體對稱性的影響，然后構建應變Ge材料導帶結構、價帶結構以及帶隙的相關數值模型，最后得到了Ge半導體的禁帶寬度與應變之間的函數關系式。

2 模型的構建

2.1 應變對Ge晶體對稱性的影響

晶體的對稱操作與系統的哈密頓量相互關聯，通過分析晶體的對稱性也能夠獲得半導體能帶結構的一些重要特征。選擇合適晶向或晶面對晶體施加適當的單或雙軸應變可以改變晶體結構的對稱性，因此，通過分析半導體晶體結構的對稱性是研究應變對半導體能帶結構影響的有效而又直觀的方法之一。

根據形變勢理論[19-21]，半導體材料所受到的應變可以分解為剪切應變和靜水應變，其中，剪切應變又可以分為兩類，一類剪切應變與x、y和z方向上的晶格常數的改變密切相關，另一類剪切應變與晶體的旋轉相關。對于立方晶系半導體而言，剪切應變降低了晶體的對稱性，從而導致了能帶的退簡并以及能帶的彎曲；而靜水應變不改變晶體的對稱性，因此它的作用僅僅使能帶發生偏移，不會清除能帶的簡并性。

圖1 (001)面雙軸張應變面心立方晶體的晶格常數模型Fig.1 Lattice constant model of face-centered cubic structure under biaxial strain paralleled to the (001) plane

綜上所述，如果我們用Ec和Eν兩個物理量表示Ge的各個導帶底和價帶頂的位置，那么對于Ge材料在(001)面雙軸張應變作用下的能帶分裂情況可以用圖2表示。

圖2 (001)面雙軸張應變鍺材料的能帶分裂示意圖Fig.2 Schematic of band splitting of Ge under biaxial strain paralleled to the (001) plane

圖2中顯示，對于雙軸張應變鍺材料，靜水應變使得導帶底和價帶頂發生了能量偏移；而剪切應變對價帶而言發生了能帶分裂現象，同時對其不同方向的導帶底也產生了不同的影響，具體為，對L和Г能谷不影響，而Δ能谷則分裂為Δ2和Δ4能谷。

2.2 應變Ge導帶模型

對于(001)晶面雙軸應變Ge材料，導帶能谷不僅有退簡并的可能，即：六度簡并的Δ能谷將退簡并為Δ2和Δ4能谷，四度簡并的L能谷和無簡并的Г能谷不發生退簡并；而且存在偏移的現象。根據形變勢理論，在平行于(001)晶面的雙軸應變作用下，鍺材料導帶L能谷、Г能谷及Δ能谷的偏移量可以表示為[14]：

(1)

(2)

(3)

(4)

由此，我們可以得到(001)晶面雙軸應變Ge材料各導帶底能級的位置：

(5)

表1 應變Ge材料能帶計算相關參數Table 1 Band parameters and deformation potentials for Ge under biaxial strain paralleled to the (001) plane

2.3 應變Ge價帶模型

由形變勢理論可知，Ge材料在平行于(001)晶面的雙軸應變作用下，價帶將發生退簡并的現象，如果考慮自旋軌道的影響，三個價帶相對于未應變Ge的情況，其能帶的分裂能差分別表示為[19-20]：

價帶輕空穴帶：

Δ0δE+9/4(δE)2]1/2

(6)

價帶重空穴帶：

(7)

價帶自旋軌道能帶：

Δ0δE+9/4(δE)2]1/2

(8)

式中：Δ0表示自旋軌道分裂能；δE=2b(ε⊥-ε‖)；b表示價帶在應力作用下的形變勢能，具體參數值見表1，單位為eV。

由此，我們可以得到(001)晶面雙軸應變Ge材料價帶頂能級的位置：

(9)

綜上所述，得到了Ge材料導帶能帶和價帶能帶與應變之間的聯系，并且建立了它們之間的具體關系表達式，這些為建立Ge材料在應變作用下的能帶結構模型提供了基礎。

3 結果與討論

由應變對Ge導帶能帶和價帶能帶影響的具體表達式就可以建立Ge材料在應變作用下的能帶結構模型。基于形變勢理論，在應變的作用下，半導體材料的能帶帶隙可以寫成：

(10)

圖3 Ge導帶各能谷的偏移量隨應變的變化趨勢Fig.3 Various strain components in conduction of biaxial strained Ge paralleled to the (001) plane as a function of in-plane strain

圖3給出了(001)晶面雙軸應變Ge材料導帶L能谷、Г能谷、Δ2能谷及Δ4能谷的偏移量隨應變的變化趨勢。從圖中可知，雙軸應變使得導帶間接帶L能谷發生偏移，偏移量與應變呈線性遞減的關系，即每增加1%的應變則間接帶L能谷下降44.9meV。具體地，相比于無應變Ge情況，在張應變的作用下，L能谷往低能方向移動；在壓應變的作用下，它將往高能方向移動。對于直接帶Г能谷，同樣只存在能級偏移的情況，并且偏移規律與L能谷類似，但每增加1%的應變則直接帶Г能谷下降121.7meV，Г能谷往低能方向偏移的速度比L能谷快1.71倍，這意味著在一定的張應變條件下，Ge將從間接帶隙材料變為以Г能谷為最低能級的直接帶隙半導體材料。導帶的Δ能谷，在(001)晶面雙軸應變作用下由未應變前的六度簡并分裂為一組二度簡并Δ2能谷和一組四度簡并Δ4能谷。其中Δ2能谷的偏移量隨應變的變化的規律與直接帶Г能谷幾乎一致。而Δ4能谷的變化情況與其它能谷正好相反，即相比于無應變Ge情況，每增加1%的應變則Δ4能谷上升45.7meV，具體為在張應變的作用下，Δ4能谷往高能方向移動，在壓應變的作用下，它將往低能方向移動。

圖4 Ge導帶Г能谷、Δ2能谷及Δ4能谷與L能谷的差值和應變之間的關系Fig.4 Energy differences between Г valley、Δ2 valley、Δ4 valley and L valley in biaxial strained Ge paralleled to the (001) plane as a function of in-plane strain

圖5 (001)晶面雙軸應變Ge材料各個價帶能級的分裂與偏移情況Fig.5 Splitting energy of valence band in biaxial strained Ge paralleled to the (001) plane as a function of in-plane strain

圖5給出了(001)晶面雙軸應變Ge材料各個價帶能級的分裂與偏移情況。從圖中可見，輕、重空穴在雙軸應變的作用下發生了退簡并，重空穴能量的偏移與應變呈線性遞減關系，每增加1%的應變則重空穴能級下降32.9meV；具體地，相比于無應變Ge情況，在張應變的作用下，重空穴能級往低能方向移動，在壓應變的作用下，它將往高能方向移動。而輕空穴能級隨著張應變的增大向高能方向移動，隨著壓應變的增大先向低能方向移動，當壓應變增大到約2%后轉向高能量方向移動。自旋軌道能帶的變化趨勢為：均隨著張、壓應變的增大而呈現非線性的向低能方向減小。

價帶輕、重空穴的退簡并不僅可以減小價帶空穴的有效質量而且也減小了空穴在輕、重空穴帶之間的散射幾率，從而提高價帶空穴的遷移率，因此應變有利于Ge溝道MOSFET器件獲得更高的性能。

圖6 Ge在(001)晶面雙軸應變下能帶偏移情況 Fig.6 Various band edge shifts as a function of in plane strain for biaxial strained (001) Ge

由于在雙軸應變的作用下，Ge的價帶輕、重空穴發生了退簡并，壓應變下相對于無應變Ge材料，重空穴會向高能量方向偏離原來位置，而輕空穴會向低能量方向偏離原來位置；而張應變情況下正好相反，因此Ge材料各個能谷的能帶寬度計算方法應該為：壓應變情況下計算各個導帶底到重空穴能帶頂的位置，而張應變情況為計算各個導帶底到輕空穴能帶頂的位置。據此，我們得到Ge材料各個能谷的能帶寬度與應變的關系如圖7所示。計算結果表明在(001)面雙軸應變作用下，鍺的能帶結構發生了重要的變化：室溫下鍺的禁帶寬度與應變的關系可以用分段函數來表示，如式(11)所示。

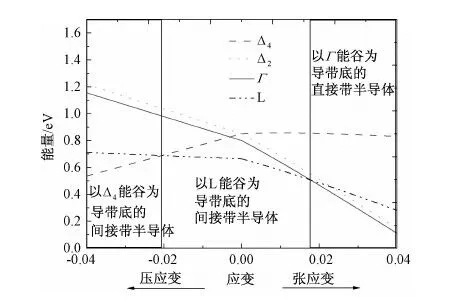
圖7 Ge材料各個能谷的能帶寬度與應變的關系Fig.7 Various band gap as a function of in plane strain for biaxial strained (001) Ge

(11)

當壓應變增加到2.06%時，Ge材料將被調控為以Δ4能谷為導帶底的間接帶半導體，此時室溫下Ge材料的禁帶寬度約為0.688eV，隨著壓應變的增大，禁帶寬度線性減小，具體為每增加1%的壓應變，禁帶寬度減小約78.63meV。當張應變增加到1.77%時，Ge材料被調控為以Г能谷為導帶底的直接帶隙半導體，禁帶寬度為0.5077eV，隨著張應變的增大，禁帶寬度線性減小，即每增加1%的張應變，禁帶寬度減小177.98meV。而應變介于-2.06%和1.77%時，Ge材料是以L能谷為導帶底的間接帶半導體，無應變Ge材料在室溫下的禁帶寬度為0.664eV，禁帶寬度隨著壓應變增加而線性增加，即每增加1%的壓應變，禁帶寬度增加11.66meV，增加幅度較小；禁帶寬度隨著張應變增加而線性減小，每增加1%的張應變，禁帶寬度減小88.29meV。

由于目前實驗室制備較高應變的Ge材料比較困難，而且應變條件下Ge材料的禁帶寬度也鮮有報道，我們將計算得到的理論值與其他研究小組的計算結果進行比較，如表2所示。主要比較的項目為Ge材料被調控為以Г能谷為導帶底的直接帶隙半導體和被調控為以Δ4能谷為導帶底的間接帶隙半導體所需要施加的具體應變值。

從文獻報道來看，各個研究小組的研究方法主要可歸為兩類：一是采用第一性原理計算能帶。該方法不需要任何經驗參數與實驗數據就能計算得到能帶結構，但從報道的結果看出，交換關聯勢的選擇會明顯影響計算結果，且該方法難與實驗結果進行比較。二是采用半經驗式的方法，如緊事縛近似、k·p微擾理論等。該方法基于實驗參數與經驗公式，相比于第一性原理的計算方法，其計算極值點附近的能帶結構已足夠精確，計算值更接近于實驗結果。我們的計算基于形變勢理論，依賴于實驗參數，因此與文獻[14,17]等結果比較吻合；同時也與文獻[15]中用密度泛函理論(DFT)計算得到的Ge從間接帶隙材料轉變為直接帶隙材料的所施加的張應變值一致，但由于DFT理論沒有考慮Δ能谷的退簡并，因此導致他們計算得到的Ge材料轉變為以Δ能谷為導帶底的間接帶半導體條件(3%壓應變)偏大。由于實驗中難以制備較高應變的Ge材料，導致計算得到的Ge材料帶隙轉變所施加的應力值結果缺乏實驗數據的驗證，還存在爭議，有待進一步的實驗研究。

表2 本文計算的理論值與文獻報道結果的對比Table 2 Comparison of calculated results from literature with various theory

4 結 論

基于形變勢理論研究了(001)面雙軸應變Ge材料的能帶結構。計算結果表明：導帶L能谷、Г能谷與雙軸應變呈線性遞減的變化關系，并且Г能谷往低能方向偏移的速度比L能谷快1.71倍，該結論表明，當張應變大于1.77%時，Ge材料被調控為直接帶隙半導體，可為制備鍺直接帶發光器件提供理論指導依據。鍺導帶Δ能谷以及價帶輕、重空穴在雙軸應變的作用下發生退簡并現象；一方面，當壓應變大于2.06%時，Ge材料被調控為間接帶半導體，以Δ能谷為導帶底，禁帶寬度隨著壓應變每增加1%而線性減小7.863eV，這說明壓應變鍺材料可用于制備MOSFET器件，以進一步提高導帶電子的遷移率；另一方面，價帶的退簡并有利于提高空穴遷移率，對制備高遷移率的鍺電子器件具有重要的理論意義。當對鍺施加的應變介于-2.06%和1.77%時，Ge是以L能谷為導帶底的間接帶半導體，禁帶寬度隨著壓應變每增加1%而增加11.66meV，增加幅度較小；禁帶寬度隨著張應變每增加1%，而線性減小84.5meV。由于目前實驗室得到的鍺材料應變值基本介于此區間，該結果對分析目前的實驗結果能起到相應的指導作用。

[1] Asghari M, Krishnamoorthy A V. Silicon Photonics: Energy-efficient Communication [J]. Nature Photonics, 2011, 5(5): 268～270.

[2] Goley P S,Hudait M K. Germanium Based Field-effect Transistors: Challenges and Opportunities [J]. Materials, 2014, 7(3): 2301～2339.

[3] Liu J F, Kimerling L C, Michel J. Monolithic Ge-on-Si Lasers for Large-scale Electronic-photonic Integration [J]. Semiconductor Science and Technology, 2012, 27(9): 094006-1～094006-13.

[4] Mitard J, Jaeger B D, Leys F E,Hellings G. Record ION/IOFFPerformance for 65nm Ge pMOSFET and Novel Si Passivation Scheme for Improved EOT Scalability [C]. 2008 IEEE International Electron Devices Meeting. San Francisco, California, USA:IEEE, 2008: 873～876.

[5] Pillarisetty R, Chu K B, Corcoran S, Dewey G. High Mobility Strained Germanium Quantum Well Field Effect Transistor as the p-channel Device Option for Low Power (Vcc=0.5 V) III-V CMOS Architecture [C]. 2010 IEEE International Electron Devices Meeting. San Francisco, California, USA:IEEE, 2010: 6.7.1～6.7. 4.

[6] Han G, Su S, Zhan C, Zhou Q. High-mobility Germanium-tin (GeSn) p-channel MOSFETs Featuring Metallic Source/drain and Sub -370℃ Process Modules [C]. 2011 IEEE International Electron Devices Meeting, Washington, DC, USA: IEEE, 2011: 16.7.1～16.7.3.

[7] Huang S, Lu W, Li C, et al. A CMOS-compatible Approach to Fabricate an Ultra-thin Germanium-on-insulator with Large Tensile Strain for Si-based Light Emission[J]. Optics Express, 2013, 21(1): 640～646.

[8] 黃詩浩,李成,陳城釗,等. N型摻雜應變Ge發光性質 [J]. 物理學報, 2012, 61(3): 036202-1～036202-8.

[9] 吳政,王塵,嚴光明,等. 采用Al/TaN疊層電極提高Si基Ge PIN光電探測器的性能[J].物理學報, 2012, 61(18): 186105-1～186105-6.

[10] Camacho A R, Cai Y, Patel N, et al. An electrically pumped germanium laser [J].Optics Express, 2012, 20 (10): 11316～11320.

[11] Koerner R, Oehme M, Gollhofer M, et al. Electrically Pumped Lasing from Ge Fabry-Perot Resonators on Si [J]. Optics express, 2015, 23(11): 14815～14822.

[12] 馬建立,張鶴鳴,宋建軍.單軸應力鍺能帶結構研究 [J]. 中國科學:物理學 力學 天文學, 2012, 42: 15～21.

[13] Moussavou M, Cavassilas N, Dib E, Bescond M. Influence of Mechanical Strain in Si and Ge p-type Double Gate MOSFETs [C]. 2015 International Conference on Simulation of Semiconductor Processes and Devices. Washington, DC, USA: IEEE, 2015: 373～376.

[14] Kurdi M E, Fishman G, Sauvage S, Boucaud P. Band Structure and Optical Gain of Tensile-Strained Germanium Based on a 30 Band K* P Formalism [J]. Journal of Applied Physics, 2010, 107: 013710-1～013710-7.

[15] Tahini H, Chroneos A, Grimes R WSchwingenschlogl U, Dimoulas A. Strain-Induced Changes to the Electronic Structure of Germanium [J]. J Phys Condens Matter, 2012, 24: 195802-1～195802-4.

[16] Yang C H, Yu Z Y, Liu Y M, et al. Dependence of Electronic Properties of Germanium on the In-plane Biaxial Tensile Strains [J]. Physica B: Condensed Matter, 2013, 427: 62～67.

[17] Chang G E, Cheng H H. Optical Gain of Germanium Infrared Lasers on Different Crystal Orientations [J]. Journal of Physics D: Applied Physics, 2013, 46: 065103-1～065103-14.

[18] Liu L, Zhang M, Hu L J, et al. Effect of Tensile Strain on the Electronic Structure of Ge: A First-Principles Calculation [J]. Journal of Applied Physics, 2014, 116: 113105-1～113105-6.

[19] Walle C G,Martin R M. Theoretical Calculations of Heterojunction Discontinuities in the Si/Ge System [J]. Physical Review B, 1986, 34(8): 5621～5634.

[20] Walle C G. Band Lineups and Deformation Potentials in the Model-Solid Theory [J]. Physical Review B, 1989, 39(3): 1871～1883.

[21] Sun Y, Thompson S E, Nishida T. Physics of Strain Effects in Semiconductors and Metal-oxide-semiconductor-field-effect Transistors[J].Journal of Applied Physics, 2007, 101(10): 104503-1～104503-22.

[22] Ishikawa Y, Wada K, Liu J. Strain-Induced Enhancement of Near-Infrared Absorption in Ge Epitaxial Layers Grown on Si Substrate [J]. Journal of Applied Physics, 2005, 98(1): 013501-1～013501-9.