基于序優化的多傳感器協同雷達輻射控制

李 波, 李卿瑩, 高曉光, 張春燕

(西北工業大學電子信息學院, 陜西 西安 710072)

0 引 言

隨著多傳感器管理(multi-sensor management, MSM)技術的不斷發展與進步[1-2]及飛機隱身性能和反隱身技術的不斷提高[3-4],對多傳感器協同(multi-sensor collaboration, MSC)探測[5-6]的研究已成為熱點。多傳感器系統(multi-sensor system,MSS)由主動傳感器和被動傳感器2部分構成,且系統內各傳感器有著不同的作用范圍和功能。主動傳感器即為機載雷達,可以同時探測目標的角度和距離信息;被動傳感器只能獲取目標的角度信息,如機載紅外搜索跟蹤(infrared search and track, IRST)系統、電子支援措施(electronic support measure, ESM)等,對各傳感器探測到的目標信息進行融合,能夠有效提升載機探測、跟蹤目標的能力[7]。但是,雷達開機會向外界輻射電磁波,容易被敵方偵察機偵察或干擾,因此應盡可能地減少雷達的開機輻射時間[8]。采用雷達與被動傳感器協同探測,在保證跟蹤精度的條件下,盡可能減少雷達的開機時間,不僅可以提高飛機的探測和跟蹤能力,還可以提高飛機的隱蔽性。

20世紀70年代,文獻[9]在傳感器管理中采用線性規劃的方法進行傳感器-目標分配。到了90年代,通信與傳感器技術大力發展,但直接對信息進行融合的傳統方法因平臺運動、分布位置、通信帶寬、計算能力和能量等的限制而無法有效實施。90年代初期,SM的研究在國外逐漸成為熱潮。文獻[10-11]在傳感器管理(sensor management,SM)中應用了信息論(information theory, IT)中熵的概念。國外對于MSM算法的研究,應用了許多領域的技術[12-16]。

國內對SM算法的研究起步比較晚。文獻[17]通過分析作戰效能論證了MSC下的雷達猝發探測技術在未來空戰中具有可實施性;文獻[18]在輻射限制下對有/無源傳感器進行管理,協同目標跟蹤;文獻[19]在目標跟蹤過程中通過比較距離測量熵與距離估計信息熵對雷達開關機進行實時控制;文獻[20]提出了通過比較跟蹤的預測協方差、預定門限來控制雷達輻射的方法;文獻[21]則對在雷達輻射控制(radar radiation control, RRC)基礎上所構建的異類MSS綜合與管理方法進行了研究；文獻[19-21]都采用雷達實時輻射控制方式但并未對輻射控制因子進行優化求解；文獻[22]研究設計了主被動雷達協同探測跟蹤模式,并提出改進的自適應交互式多模型不敏濾波算法。近年來,國內關于MSC跟蹤的研究雖有一定突破性進展和成果[23-24],但在其理論創新與應用實踐方面仍然還有許多關鍵技術問題需要深入研究和解決。

本文提出雷達混合輻射控制(radar mixed radiation control, RMRC)方式,并找出符合要求的雷達輻射周期Tc和輻射控制因子k最優的組合,使得MSC探測跟蹤過程中在保證跟蹤精度的同時盡量減小雷達開關機次數以提高作戰飛機電磁隱身性能。在跟蹤過程中,采用交互式多模型(interaction multiple model,IMM)算法[25-26]實現對單目標的跟蹤,利用擴展卡爾曼濾波(extend Kalman filter,EKF)算法[25]對跟蹤結果進行濾波,建立了MSC下RRC的參數優化模型。在等間隔控制、實時控制和混合控制下分別進行仿真,得出結論。

1 MSC下RRC方式

1.1 等間隔控制方式

雷達的等間隔輻射是最簡單的輻射控制方式。在該控制方式下,雷達采用固定的輻射周期Tc進行輻射,且輻射周期是離線計算的。其基本思想為:在確定的作戰條件下,根據已知的傳感器量測誤差及預測所需的跟蹤精度,考慮不同的目標類型、目標距離、戰斗需要等因素,離線計算出針對某種目標的雷達等間隔輻射周期Tc。該控制方式比較簡單,實現也比較容易。

1.2 實時控制方式

由于雷達輻射的等間隔控制方式不僅需要離線計算出輻射周期Tc,而且需要對目標類型做出判斷,因此不確定性較大。而且在這種輻射周期固定的工作方式下,雷達可能在被動傳感器單獨對目標跟蹤效果很好的情況下開機工作,此時雷達對跟蹤效果的幫助較小,反而向外輻射電磁波,這樣不僅造成了輻射資源的浪費,還增加了我方被敵方偵察跟蹤的風險;反之,雷達可能在被動傳感器對目標跟蹤效果較差的情況下不開機,這樣就不能滿足對目標的跟蹤要求,嚴重時還可能造成目標丟失。因此提出一種比較靈活的實時控制方式,雷達是否發射電磁波主要由系統對目標跟蹤的實時效果進行評估決定。該方法是通過比較目標濾波殘差范數d(k)與門限從而實現雷達開關機的實時控制。根據濾波理論,d(k)服從自由度為m(m為觀測維數)的卡方分布,由此通過濾波殘差控制雷達開關機就相當于一個假設檢驗問題,即檢驗d(k)是否位于以m為中心的置信區間(m-kσd(k),m+kσd(k))內。k為決定置信區間長度的系數,稱其為輻射控制因子。

1.3 混合控制方式

由于雷達輻射的實時控制方式中雷達的開機次數過于頻繁,易被敵方探測跟蹤,不利于我機的隱身性。因此提出一種混合控制方式,將等間隔控制和實時控制結合起來,即雷達采用固定的輻射周期Tc,同時利用目標殘差范數來確定雷達是否開機。這樣既可以避免雷達以固定輻射周期探測帶來的靈活性差和目標丟失等問題,同時又避免了每次量測更新時目標殘差范數計算量大及雷達開機次數過多的缺點。在混合控制方式下,要避免丟失目標,應盡量使雷達輻射周期小。MSC下雷達混合控制方式流程如圖1所示。

圖1 混合控制流程圖Fig.1 Flow chart of hybrid control

2 MSC下RRC參數優化模型

2.1 基于IMM-EKF的MSFT算法

本文的MSS采用勻速直線運動、勻速左轉彎和勻速右轉彎3種模型對目標進行協同跟蹤,交互式多模型-擴展卡爾曼濾波(interaction multiple model-extend Kalman filter,IMM-EKF)算法對這3種模型進行交互跟蹤。

假設目標運動的狀態方程為

xt+1=Φtxt+wt

(1)

在勻速運動(constant velocity, CV)模型假設下有

(2)

在勻速轉彎(constant turn, CT)模型假設下有

(7)

觀測方程為

zt=h[xt]+vt

(8)

式中,T為傳感器的采樣周期;ω為勻速轉彎的角速度;zt為觀測向量;vt為服從高斯分布的白噪聲,即:vt～N(0,Rt),Rt為觀測噪聲協方差矩陣。wt和vt相互獨立,系統的觀測方程為非線性方程。針對不同的傳感器,量測的量不同,故觀測方程有不同的形式,具體如下:

主動傳感器可以測量目標的距離r、方位角θ和俯仰角φ,即

(9)

被動傳感器只能測量目標的方位角θ和俯仰角φ,即

(10)

基于IMM-EKF的多傳感器融合跟蹤(multi-sensor fusion tracing,MSFT)算法如圖2所示。

圖2 基于IMM-EKF的MSFT算法Fig.2 MSFT algorithm based on IMM-EKF

2.2 RMRC參數優化模型

RMRC就是要在保證對目標跟蹤精度的條件下,盡可能地減少雷達開機次數。在RMRC策略下,雷達以一定的輻射控制周期Tc和輻射控制因子k共同完成雷達的開關機控制過程。在MSC對目標進行跟蹤過程中,輻射周期Tc越小,量測信息越充分,目標跟蹤精度越高;輻射周期Tc越大,雷達工作次數越少,目標跟蹤精度越低;輻射控制因子k越小,置信區間越大,雷達開機次數越多,目標跟蹤精度越高;輻射控制因子k越大,置信區間越小,雷達開機次數越少,目標跟蹤精度越低,即雷達輻射周期Tc大小和輻射控制因子k大小將直接影響到對目標的協同跟蹤效果。

(11)

(12)

式中,Pj為第j次濾波得到的狀態誤差協方差矩陣;Ns為濾波次數,由跟蹤時間和采樣周期共同決定,即Ns=Ttrack/Ts。

基于MSC的RRC問題,就是確定出最佳的參數組合,使得MSC目標跟蹤精度盡可能接近期望跟蹤精度,即

(13)

上述優化問題保證了目標跟蹤精度在高于期望跟蹤精度的前提下,盡可能接近期望跟蹤精度,這樣能夠在保證跟蹤精度的同時,盡量減少雷達開機時間,提升電磁隱身性能。式(13)中的目標函數和約束條件都不能顯式給出,要借助IMM-EKF的迭代仿真計算得出。因此,上述優化問題可以采用基于仿真的優化方法進行求解。

3 基于OO的RRC參數優化模型求解

對于單目標復雜優化問題,通常其解空間具有復雜的結構,且隨著問題規模增大,其解集大小也會呈指數級增大。因此,需要大量的時間進行仿真計算,且常常得不到滿意的解。

1992年,文獻[27-31]最先提出了序優化(ordinal optimization, OO)理論。作為一種求解單目標復雜優化問題的有效工具,其基本思想包含排序比較和目標軟化,實際工程中的問題往往比較復雜、求解規模較大且解空間結構比較復雜,而OO理論方法在解決這類復雜問題時具有更強的能力,可以有效提高計算效率。

一般地,OO理論將單目標優化問題分為5種類型:Neutral型、Bell型、Steep型、U-shaped型和Flat型,分別對應的有序性能曲線(ordered performance curve,OPC)[31]如圖3所示。根據問題所對應的OPC可以確定優化問題的類型,就可以根據相應的原則求解足夠好的優化方案。

圖3 OO OPCFig.3 OPC of OO

RRC參數優選的OO求解步驟如圖4所示。

圖4 RRC參數優選的OO步驟Fig.4 OO steps of RRC parameter optimization

OO的具體流程為:

(1)按機會均等原則從解空間中隨機抽取M組(Tc,k)i(i=1,2,…,M)的值,其中Tc∈[Tc min,Tc max],k∈[kmin,kmax]。將這M組數據輸入到細模型(即IMM-EKF算法)中進行計算,得到M組估計誤差協方差矩陣Pi。

(3)將M組目標函數值和輸入進行曲線擬合得到優化問題的粗模型y=g(Tc,k)。

(4)重新按機會均等原則從解空間中隨機抽取N組(Tc,k)j(j=1,2,…,N)的值構成表征集合,將這N組數據輸入擬合得到的粗模型中進行仿真計算,對輸出yj進行排序比較,并繪出其OPC,得到OPC曲線的類型。

(5)將OPC類型所對應的z,ρ,γ,η結合式Z(m,g)=ezmρgγ+η確定選定集合S的大小s。

(6)從粗模型的輸出中由小到大選取s組輸出對應的輸入(Tc,k)n(n=1,2,…,s),將這s組數據代入細模型中進行計算,對輸出的目標函數值f(Tc,k)n(n=1,2,…,s)進行排序,從小到大選取m個值,輸出這m個值對應的(Tc,k)值即為所求的足夠好的解。

其中曲線擬合所用的方法為最小二乘擬合法,對于前面所述的RRC參數優化模型的最小二乘擬合,有

(14)

式中,(a1,a2,…,a6)為待定系數。

4 仿真分析

4.1 仿真環境

用于仿真的計算機性能指標如表1所示。

表1 仿真計算機性能

4.2 仿真初始條件設置

過程噪聲協方差矩陣為Qk=diag[100,10,50,5,100,10],量測噪聲協方差矩陣為Rk=diag[100,10,50,5,100,10]。期望協方差矩陣Pd=diag[200,30,150,20,100,10]。

對于3種模型:CV模型、勻速左轉彎模型和勻速右轉彎模型,模型概率為u=[0.4,0.3,0.3]T,模型轉移概率矩陣為

(15)

總的仿真時間為200 s,且目標在20～60 s做勻速左轉彎運動;在110～150 s做勻速右轉彎運動;在其余時間則做勻速直線運動。仿真的采樣時間T=1 s,目標在作勻速左轉彎和勻速右轉彎角速度分別為ω1=3 rad/s和ω2=-3 rad/s。假設整個過程中工作的傳感器有3種:ESM系統、IRST系統和機載雷達。ESM一直處于工作狀態,IRST的工作周期為3 s,雷達的工作周期為Tc。

4.3 OO求解

從解空間Tc∈[0.5,10],k∈[0.05,1]中Tc按0.5的步長、k按0.05的步長取值時,M=400,由混合控制方式得到的仿真結果如下:

將輸入Tc、k及IMM-EKF的輸出f(Tc,k)作為坐標系的3個軸,畫出的三維圖形如圖5所示。擬合得到的待定系數如表2所示。

從解空間Tc∈[0.1,10],k∈[0.01,1]中選出N=10 000組輸入代入粗模型(即g(Tc,k))中進行計算,其中Tc按步長0.1、k按步長0.01來選取。最終得到的10 000組解按從小到大排序后,在直角坐標系中畫出的OPC曲線如圖6所示。

圖5 Matlab擬合得到的三維圖形Fig.5 3D graphics fit by Matlab

a1a2a3a4a5a6-2.074 2228.863 043.575 88.707 6-16.575 3148.912 2

圖6 OPC曲線Fig.6 OPC curve

當m=5,g=50時,噪聲特性U=1時,由Z(m,g)=ezmρgγ+η得到的選定集合ΘS的大小s=83。最終得到足夠好的5個解、對應的目標函數值f(Tc,k)和程序運行時間如表3所示,序號為1的解為5個解中的最優解。

表3 混合控制方式得到的足夠好的解

同理,由OO的方法在等間隔輻射控制方式和實時控制方式下得到最優解,3種控制方式下的最優解情況如表4所示。

表4 3種控制方式得到的最優解

將等間隔控制、實時控制和混合控制方式得到的最優解分別代入IMM-EKF算法中,得到3種控制方式下的跟蹤誤差和雷達開機次數。3種控制方式的位置跟蹤誤差如圖7所示。

圖7 3種控制方式的位置跟蹤誤差Fig.7 Tracking error of three control methods

由圖7可以看到,實時控制方式的跟蹤誤差最小,跟蹤性能最好;等間隔控制方式下的跟蹤誤差最大;混合控制方式下的跟蹤誤差則介于實時控制和等間隔控制之間。

圖8 等間隔控制下雷達開機次數Fig.8 Radar boot times of equal interval control

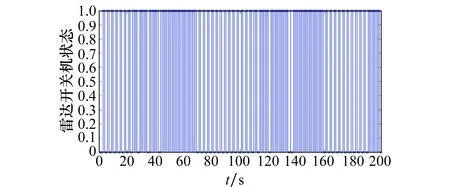
圖9 實時控制下雷達開機次數Fig.9 Radar boot times of real-time control

圖10 混合控制下雷達開機次數Fig.10 Radar boot times of hybrid control

而由圖8～圖10可以看到,實時控制的雷達開機次數最多,很容易被敵方偵察與截獲,而等間隔控制的開機次數次于實時控制,混合控制的雷達開機次數最少。綜上,混合控制方式可以在保證雷達開機次數較少的情況下又能達到比較好的跟蹤性能。

5 結 論

本文提出MSC下的RMRC方法,基于IMM-EKF跟蹤濾波算法對MSC下的RRC問題進行建模分析,基于OO方法在Matlab環境下對該模型進行仿真求解,并對仿真結果進行分析。對等間隔控制、實時控制和混合控制方式下的參數進行優化,比較了3種控制方式的跟蹤結果。仿真結果證明了混合控制方式的相對優勢。該方法應用于未來空戰的復雜戰場環境,能夠在保證作戰效能的前提下有效降低我方戰機的被探測概率,具有較強的實戰應用價值。

參考文獻：

[1] BIER S G, ROTHMAN P L, MANSKE R A. Intelligent sensor management for beyond visual range air-to-air combat[C]∥Proc.of the IEEE Aerospace and Electronics Conference, 1988: 264-269.

[2] 胡笑旋, 張強. 多傳感器協同管理機制研究[C]∥中國儀器儀表學會青年學術會議, 2007. HU X X, ZHANG Q. Research on multi-sensor synergistic management mechanisms[C]∥Proc.of the China Instrument Society Young Academic Conference, 2007.

[3] 徐雅薇,謝曉竹.多傳感器圖像融合方法及應用綜述[J].四川兵工學報,2015,7(10):116-119.

XU Y W, XIE X Z. Overview of approaches and applications of multi-sensor image fusion[J].Journal of Sichuan Ordnance,2015,7(10): 116-119.

[4] 劉寧波,孫艷麗,周偉.無人機多傳感器協同探測演示系統設計[J].兵器裝備工程學報,2016,37(12):80-83.

LIU N B, SUN Y L, ZHOU W. Design for multi-sensor collaborative reconnaissance of unmanned aerial vehicle demonstration system[J].Journal of Ordnance Equipment Engineering, 2016, 37(12):80-83.

[5] 趙建恒, 許蘊山, 鄧有為,等. 一種面向協同探測的多傳感器管理系統架構[J].電光與控制, 2015(6): 6-10.

ZHAO J H, XU Y S, DENG Y W, et al. An architecture of multi-sensor management system for cooperative detection[J]. Electronic Optics and Control, 2015(6): 6-10.

[6] 武龍,許蘊山,龍文彪.一種多傳感器協同探測的雷達跟蹤系統[J].空軍工程大學學報(自然科學版),2017, 18(1):39-43.

WU L, XU Y S, LONG W B. A radar tracking system based on cooperative detection of multi-sensor resource[J]. Journal of Air Force Engineering University (Natural Science Edition), 2017, 18(1):39-43.

[7] SHAHBAZIAN E, BARIL L, MICHAUD G, et al. Analysis of adaptive data fusion approaches within lm canada’s technology demonstrator[C]∥Proc.of the RTO IST Symposium on Military Data and Information Fusion, 2003: 11.

[8] 貴彥喬,吳彥鴻,俞道濱. 跟蹤雷達干擾技術綜述[J].兵器裝備工程學報,2017,38(4):141-147.

GUI Y Q,WU Y H,YU D B. Review of jamming techniques to tracker radar[J].Journal of Ordnance Equipment Engineering,2017,38(4):141-147.

[9] NASH J M. Optimal allocation of tracking resources[C]∥Proc.of the IEEE Conference on Decision and Control, 1977:1177-1180.

[10] MANYIKA J, DURRANT-WHYTE H. Data fusion and sensor management: a decentralized information-theoretic approach[M]. Prentice Hall PTR, 1995.

[11] SCHMAEDEKE W W. Information-based sensor management[C]∥Proc.of the Optical Engineering and Photonics in Aerospace Sensing, 1993: 156-164.

[12] XIONG N, SVENSSON P. Multi-sensor management for information fusion: issues and approaches[J]. Information Fusion, 2002, 3(2): 163-186.

[13] HINTZ KENNETH J, MCINTYRE G. Goal lattices for sensor management[C]∥Proc.of the Signal Processing, Sensor Fusion and Target Recognition, 1999: 249-255.

[14] KREUCHER C, KASTELLA K, III A O H. Sensor management using an active sensing approach[J]. Signal Processing, 2005, 85(3):607-624.

[15] HILAL A R, BASIR O. A collaborative energy-aware sensor management system using team theory[M]. ACM, 2016.

[16] TANG S, BI D, XU Y, et al. Dynamic sensor management algorithm based on improved efficacy function[C]∥Proc.of the IEEE International Conference on Electronic Measurement & Instruments, 2016: 1438-1442.

[17] 劉學全, 李波, 萬開方, 等. 基于多傳感器協同的雷達猝發技術研究[J]. 中國民航大學學報, 2012, 30(6): 17-20.

LIU X Q, LI B, WAN K F, et al. Study on radar burst technology based on multi-sensor synergy[J]. Journal of Civil Aviation University of China, 2012, 30(6): 17-20.

[18] 吳巍,柳毅,王國宏,等.輻射限制下有源無源協同跟蹤技術[J].信息與控制,2011, 40(3): 418-423.

WU W, LIU Y, WANG G H, et al. Active and passive synergy tracking technique with emission constraint[J]. Information and Control, 2011, 40(3): 418-423.

[19] 吳巍, 柳毅, 楊玉山, 等. 機載多傳感器協同跟蹤與輻射控制研究[J]. 彈箭與制導學報, 2011, 31(1): 153-156.

WU W, LIU Y, YANG Y S, et al. The study on air-borne multi-sensor synergy tracking and radiation control[J]. Journal of Projectiles, Rockets Missiles and Guidance, 2011, 31(1): 153-156.

[20] 吳巍,王國宏,柳毅,等.機載雷達、紅外、電子支援措施協同跟蹤與管理[J].系統工程與電子技術,2011,33(7)：1517-1522.

WU W, WANG G H, LIU Y, et al. Airborne radar/IRST/ESM synergistic tracking and management[J]. Systems Engineering and Electronics, 2011, 33(7): 1517-1522.

[21] 鐘曉軍, 王國宏. 異類多傳感器系統中基于跟蹤質量的輻射控制研究[J]. 現代雷達, 2004, 26(2): 18-22.

ZHONG X J, WANG G H. A study on radiation control based on the tracking quality in heterogeneous sensors system[J]. Modern Radar, 2004, 26(2): 18-22.

[22] 章釗, 周峰, 張亮亮. 一種主/被動雷達協同探測跟蹤算法[J]. 空軍工程大學學報(自然科學版), 2013, 02:51-55.

ZHANG Z, ZHOU F, ZHANG L L. Research on active and passive radar synergistic detection and tracking algorithm[J]. Journal of Air Force Engineering University (Natural Science Edition), 2013, 02:51-55.

[23] 黃俊, 滕鵬, 于雷,等. C4ISR多傳感器跟蹤資源協同分配方法研究[J]. 系統仿真學報, 2009, 21(3):851-855.

HUANG J, TENG P, YU L, et al. Research on coordinated allocation of c4isr multi-sensor tracking resource[J]. Journal of System Simulation, 2009, 21(3):851-855.

[24] 馬霞, 吳必富. 輻射控制下多機多傳感器協同目標跟蹤的分配決策數學模型[C]∥中國指揮控制大會, 2015.

MA X, WU B F. Mathematics model for multi-aircraft multi-sensor coordinated tracking target assignment policy with emission control[C]∥Proc.of the China Command and Control Conference, 2015.

[25] 戴春亮,時晨光,周建江,等.基于無源傳感器協同的機載雷達自適應輻射控制算法[J].數據采集與處理,2016,31(4):746-753.

DAI C L, SHI C G, ZHOU J J, et al. Adaptive radiation control algorithm with passive sensor cooperation in airborne radar system[J]. Journal of Data Acquisition and Processing, 2016, 31(4): 746-753.

[26] 吳衛華, 江晶, 高嵐. 機載雷達輔助無源傳感器對雜波環境下機動目標跟蹤[J]. 控制與決策, 2015, 30(2): 277-282.

WU W H, JIANG J, GAO L. Tracking maneuvering target in clutter with passive sensor aided by airborne radar[J]. Control and Decision, 2015, 30(2): 277-282.

[27] LAU T W E, HO Y C. Universal alignment probabilities and subset selection for ordinal optimization[J]. Journal of Optimization Theory and Applications, 1997, 93(3): 455-489.

[28] DENG M, HO Y C, HU J Q. Effect of correlated estimation errors in ordinal optimization[C]∥Proc.of the ACM 24th Conference on Winter Simulation, 1992: 466-474.

[29] DENG M, HO Y C. Iterative Ordinal optimization and its applications[C]∥Proc.of the 36th IEEE Conference on Decision and Control, 1997, 4: 3562-3567.

[30] LI D, LEE L H, YU C H. Constraint ordinal optimization[J]. Information Sciences, 2002, 148(1):201-220.

[31] 李波,劉學全,高曉光.基于BP網絡和序優化方法的火控攻擊方案尋優[J].系統工程與電子技術,2013,35(9):1886-1990.

LI B, LIU X Q, GAO X G. Fire control attack scheme optimization based on BP network and ordinal optimization[J]. Systems Engineering and Electronics, 2013, 35(9): 1886-1990.