就醫排隊問題中的模型研究
惠曉萍 單海華


摘 要:通過研究排隊論的理論知識在醫療資源優化配置中的應用范圍和條件,建立其醫院門診排隊系統的數學模型,為醫院的發展提出有益的參考。
關鍵字: 排隊論醫院門診
隨著社會經濟的發展以及人們生活水平的提高,公眾對于醫療健康保障的需求與日俱增。但目前我國的醫療資源,特別是優質資源仍然十分緊張,排隊就醫已成為一種普遍現象。當就醫等待時間過長,患者滿意度下降,易引發醫患矛盾,因此對如何優化醫療資源配置進行研究是很有必要的。排隊論(Queuing Theory),又稱隨機服務系統理論,是通過研究各種服務系統在排隊等待現象中的概率特性,從而解決系統最優設計與最優控制的一門學科 [1]。近年來,排隊論被引入醫療服務領域,與模擬仿真技術相結合,為緩解排隊等候擁擠現象提供了有效的方案。
1 門診排隊系統的構成
一般的排隊系統有三個基本部分:顧客的到達(輸入)、排隊規則以及服務機構(圖1)
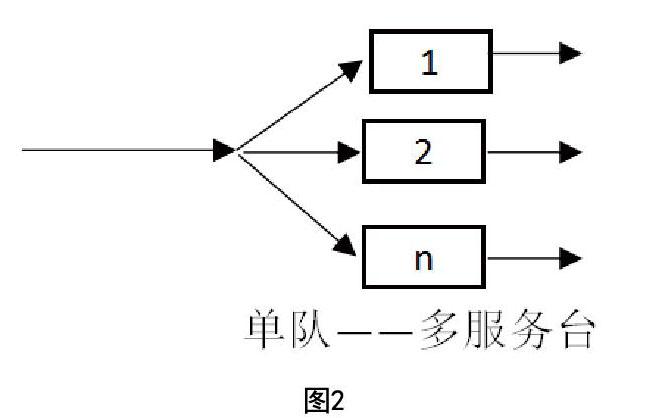
在醫院門診系統中,顧客即為前來就診的患者,患者到達醫院的時間是隨機的,相互獨立的。在接受服務前,患者需排隊等待,隊列按其能容納的最大顧客數分為有限隊長和無限隊長[2],醫院的門診隊列視為無限隊長。等待結束后,患者進入診室就診,在綜合性醫院,診室的不是唯一的,而是多名醫生同時坐診,所以是單隊——多服務臺的結構模式(圖2)。
2 門診排隊系統的模型應用
因為門診病人到達的次序是隨機、獨立的,所以大多數情況下,患者的分布服從泊松分布,且根據病程的輕重不同,其診療時間較好的擬合了負指數分布,所采用的模型為M/M/c模型。M/M/c模型即多服務臺的排隊系統,指患者到達的間隔時間和所接受服務的時間均服從負指數分數,服務機構為c個獨立的服務臺,且平均服務率相同,都為。記為服務系統的平均利用率,當時,系統到達率等于離去率,處于平衡狀態,反之則要排隊等候,此時系統的穩態概率為
3 排隊模型的計算機仿真
在排隊論的基礎上,運用計算機仿真對醫院門診這一復雜的排隊系統的結構進行動態模擬,以獲得關鍵的數量指標,進而進行分析和預測,從而為決策者提供依據。目前常用的仿真軟件有Flexsim以及Matlab的Simulink。
Flexsim是美國Flexsim公司的產品,它采用C++語言開發,采用面向對象編程和Open GL技術,提供三維圖形化建模環境,可以直接建立三維仿真模型,它支持就醫排隊這類離散型問題的系統建模。
Simulink是Matlab的仿真模塊,它是一個用來對動態系統進行建模、仿真和分析軟件包,它支持線性和非線性系統,能夠在連續時間域、離散時間域進行建模。通過編寫S-函數建立仿真模型,確定仿真輸入和輸出的參數,進行動態仿真,該程序可移植性強,調試簡單,便于研究分析。此方法對于提高工作效率,解決實際問題具有一定的幫助。
有效利用排隊模型,一方面可以幫助解決醫院服務系統中人員的設備的優化配置,為醫院決策者提供參考依據,另一方面通過系統優化,找出患者和醫院間的平衡點,既減少患者的排隊等待時間,又防止醫院資源的浪費,從而盡力獲取最大的社會效益和經濟效益。
參考文獻
[1]李軍,徐玖.運籌學[M].北京:科學出版社,2003,42-43
[2] Chaussalet T J,Xie H,Millard P. A closed queuing network approach to the analysis of patient flow in health care systems.[J].Methods InfMed,2006,45(5):492-497
作者簡介
惠曉萍,女,江蘇蘇州人,講師,碩士,研究方向為社會醫學與衛生事業管理。

