基于光滑攻角剖面的高超聲速滑翔飛行器下降段軌跡設計

李天任，雷建長，王宇航，周 華，黃 佩

0 引 言

近年來，國內外學者對高超聲速飛行器再入軌跡優化與制導開展了大量研究：一類是傳統的返回艙式低升阻比再入飛行器，常采用傾側角反轉的軌跡優化和制導方法；另一類是近年來發展的高升阻比滑翔飛行器，一般采用攻角、傾側角作為控制變量，通過設計兩者在再入過程中隨時間、速度、高度的變化規律來滿足過程、終端狀態約束，同時達到某一性能指標最優。

目前，離線進行優化的偽譜法是較為成熟的再入體軌跡設計方法。偽譜法通過在整條軌跡的配點處離散，將再入動力學微分方程轉化為代數方程，最后采用序列二次規劃（Sequential Quadratic Programming，SQP）等方法求解非線性規劃問題。其在單機上進行一次軌跡設計的計算時間較長，一般用于離線生成標稱軌跡。

為了發揮高升阻比飛行器的在線機動能力，水尊師[1]和肖紅[2]等人發展了基于航路點的局部預測校正制導方法，但其離線設計的航路點是固定的，削弱了飛行器軌跡的變更、再生成能力。基于Harpold[3]的航天飛機再入軌跡設計思路，周浩[4]、李強[5]、劉運鵬[6]等人采用常值、分段線性等攻角設計方案，用于軌跡的初步設計和在線預測。另一方面，胡錦川[7]的平穩滑翔軌跡以及張冉[8]均要求攻角曲線連續且可導，在使軌跡平穩的同時降低飛行器姿態控制器的設計要求。

下降段是再入飛行器進入大氣層后的初始飛行階段，也被稱為引入段。為了在下降段軌跡的設計中簡化控制量曲線的設計，同時增強控制量剖面的光滑度，易于與平衡滑翔段軌跡光滑對接，除了現有的常值、分段線性以及復合指數函數的剖面設計方案外，有必要引入新的函數形式。本文采用改進的復合三角函數，其具有幅值可調、波峰的位置和峰形可變、導數連續且光滑等優點，適合在控制量剖面設計中采用。

1 再入動力學模型

針對無動力再入飛行器，在位置系下建立動力學模型，O-XYZ為地心固連坐標系，將其繞Z軸正向旋轉經度θ，再繞新的 Y軸旋轉緯度φ得到位置坐標系O-xyz，如圖1所示。

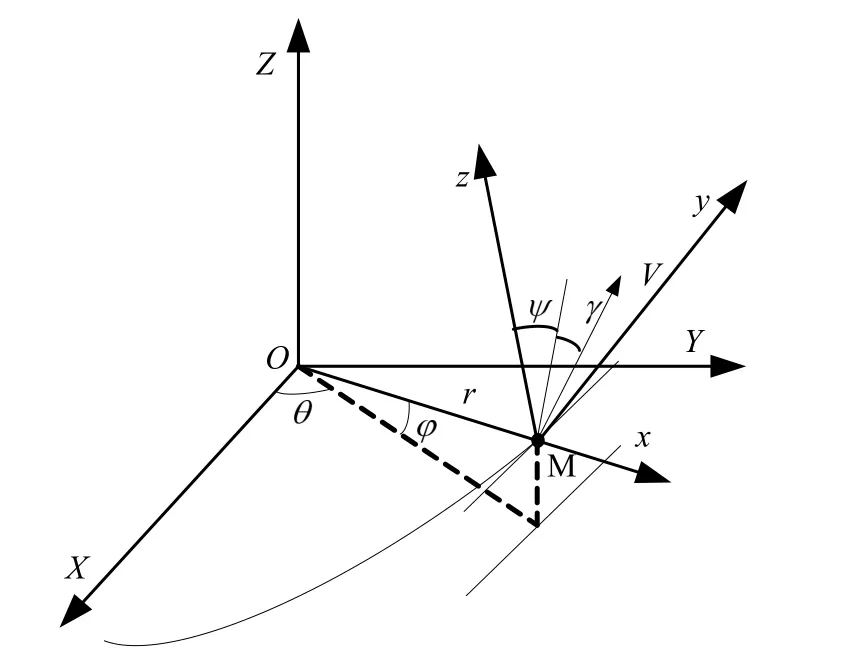
圖1 三自由度運動參數示意Fig.1 3D Motion Parameters Diagram

采用圓球無旋地球假設，飛行器動力學方程[9]為

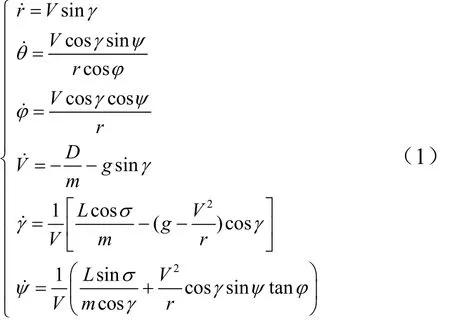
式中 r，θ，φ，V，γ，ψ分別為地心距、經度、緯度、速度、彈道傾角、航向角；g為重力加速度；m為飛行器質量；σ為傾側角；L，D分別為升力和阻力，且，

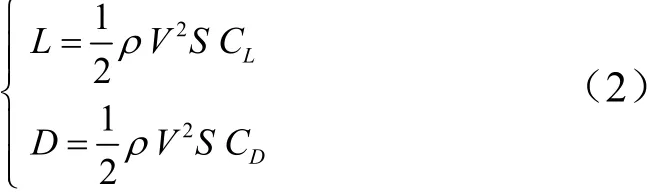
式中 ρ為大氣密度；S為參考面積； CL， CD分別為升力系數、阻力系數。

m，S，CL, CD均參考國外滑翔飛行器CAV-H，m=907 kg，S=0.4839 m2。對升力系數 CL和阻力系數 CD進行擬合，得到兩者對攻角α的關系式[10]：

在再入飛行器初始下降段，常采用零傾側角、大攻角拉起的方案，在飛行器狀態參數滿足一定條件時，切換到平衡滑翔階段，隨后采用平衡滑翔段的攻角、傾側角剖面。本文采用的切換條件為

式中1K為彈道傾角的權系數；ε為一小量。

采用下降段零傾側角、單波峰攻角剖面，平衡滑翔段的攻角剖面由擬平衡滑翔條件（Qusi Equilibrium Glide Condition，QEGC）推導得到。根據擬平衡滑翔條件：

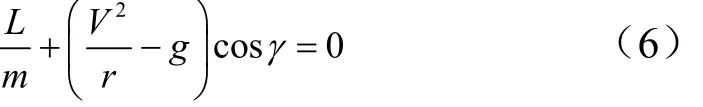
根據當前狀態已知的 V ,r,g，聯立式（2）、式（3）、式（6），得到擬平衡滑翔攻角 αQEGC為

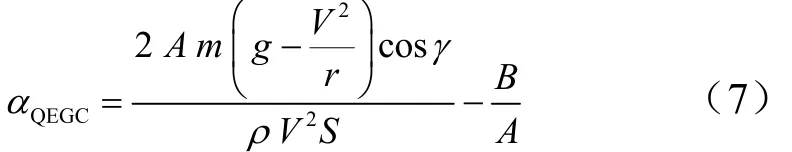
式中 A，B為式（3）中攻角的一階項系數和常數項。

考慮到氣動系數誤差，在 αQEGC上反饋彈道傾角的誤差項 Δ α= K2(γ -γ*)，其中，γ*為平衡滑翔段跟蹤的彈道傾角， K2為反饋增益系數。由于本文研究的重點不是平衡滑翔段，可取γ*=-0.05°，從而有：

仿真結果表明，該方法能夠在考慮各項偏差的情況下生成擬平衡滑翔軌跡。

2 下降段控制量剖面設計方法

2.1 下降段控制量設計思路

下降段攻角剖面常采用最大攻角、分段線性等攻角方案[3～5]，在與滑翔段的對接處難以連續和可導，使軌跡平穩性降低、同時對姿態控制器的設計提出了很高要求。此外，大量的彈道仿真表明不連續或不可導的控制量剖面常導致對接點過載和熱流峰值較大，難以滿足過程約束。

考慮在再入下降段采用改進的復合三角函數，以增強對接點光滑性、降低最大過載和熱流峰值。

2.2 單波峰攻角剖面生成方法

再入飛行器下降到一定高度，采用如下攻角時序：

式中mα為飛行器最大可用攻角。根據CAV-H的氣動系數表[10]，mα取20°，()Ft采用時間t的二次多項式函數：

通過調節多項式系數 ai(i = 0 ,1,2)來調整波長、波形和波峰位置，生成廣義正弦函數簇，見圖2。

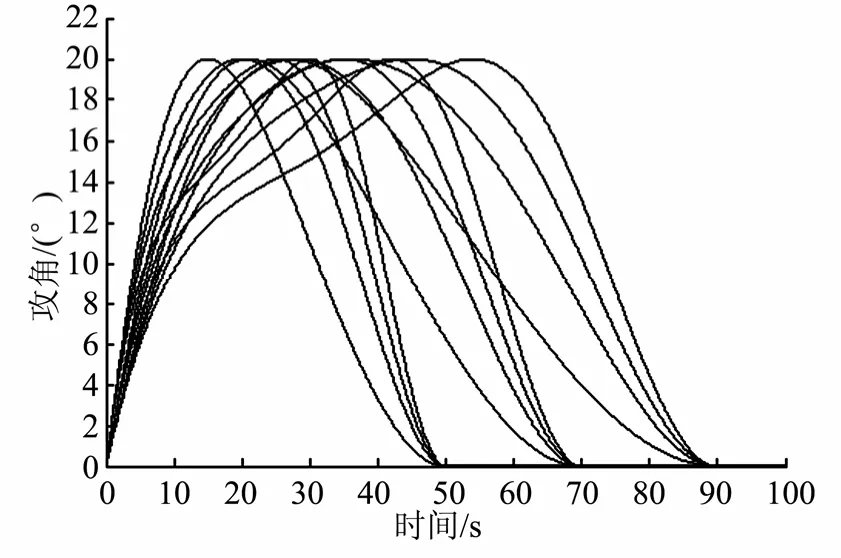
圖2 不同波長、波峰位置的三角函數簇Fig.2 Trigonometric Functions with Diffierent Wavelength and Peak Position

2.3 搜索過渡點光滑的攻角剖面

為了增強下降段與平衡滑翔段過渡點處的攻角剖面光滑性，需要優化控制下降段攻角剖面形狀的ai(i = 0 ,1,2)3個參數。本文采用改進的差分進化算法（Differential Evolution，DE）[11]進行參數尋優。目標函數見式（11）。

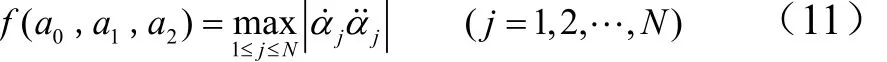
式中 j表示第j個積分區間，積分區間個數 N = tf/h ，tf，h為積分結束時間和積分步長。本文在Storn[11]的交叉操作之后增加拉回步驟，拉回不在解空間的新個體，以增強算法的魯棒性。

3 數值仿真及分析

3.1 攻角剖面光滑性驗證

CAV-H 再入點參數取 H=70 km，V=7.5 km/s，γ=-2°。下降段采用復合三角函數的攻角剖面，平衡滑翔段采用擬平衡滑翔攻角，以控制量光滑性為目標函數進行參數優化，得到如圖3所示的攻角曲線。

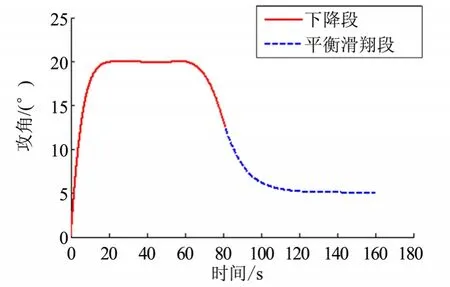
圖3 分段的攻角曲線Fig.3 Segment Curve of Angle of Attack

檢查攻角剖面光滑性，見圖4、圖5。結果表明，攻角剖面在下降段前期與傳統最大正攻角方案一致，而在過渡點附近與平衡滑翔段光滑銜接，攻角、攻角一階導數均連續。攻角剖面一階導數大小在過渡點附近不超過1 (°)/s，二階導數大小在過渡點附近不超過2 (°)/s2，基本滿足張冉[8]對攻角光滑性的要求。

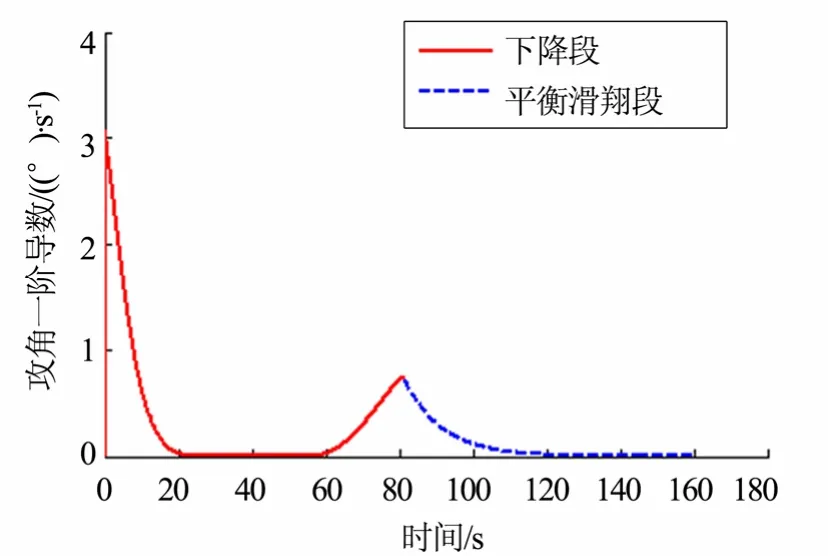
圖4 攻角一階導數Fig.4 First Derivative of Angle of Attack

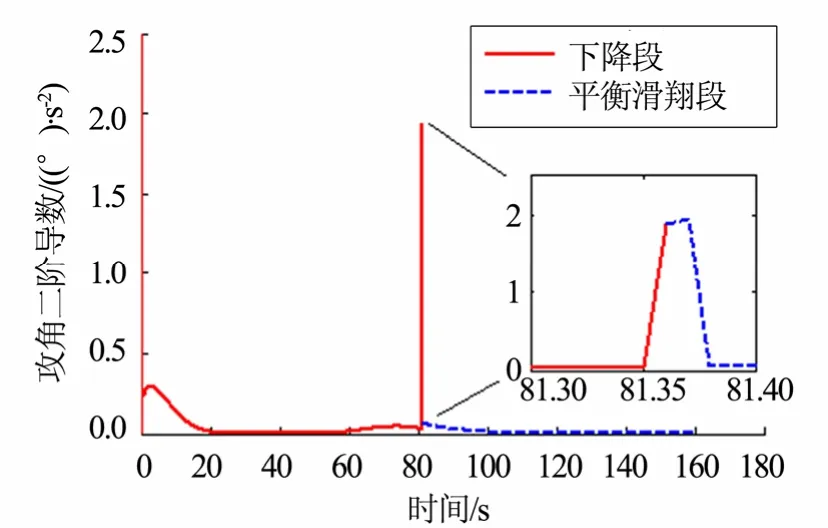
圖5 攻角二階導數Fig.5 Second Derivative of Angle of Attack

采用優化后的攻角剖面對CAV-H飛行器的再入下降段和平衡滑翔段進行數值仿真，見圖6、圖7。

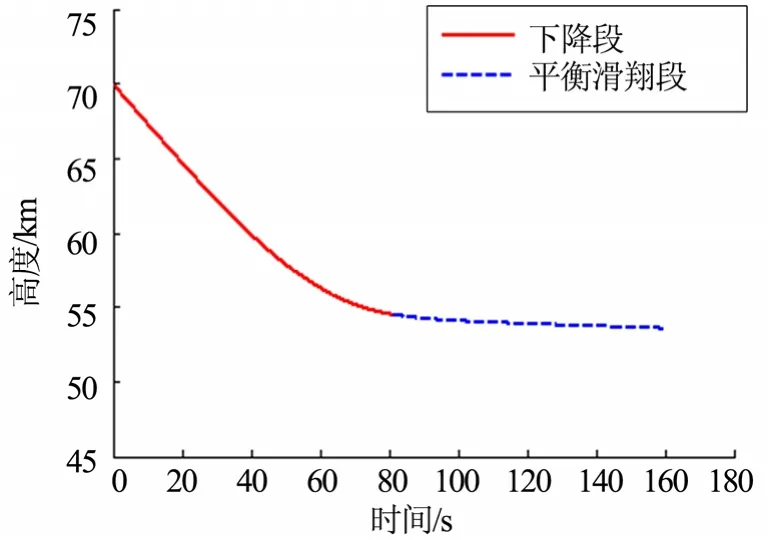
圖6 高度-時間曲線Fig.6 Hight-Time Curve

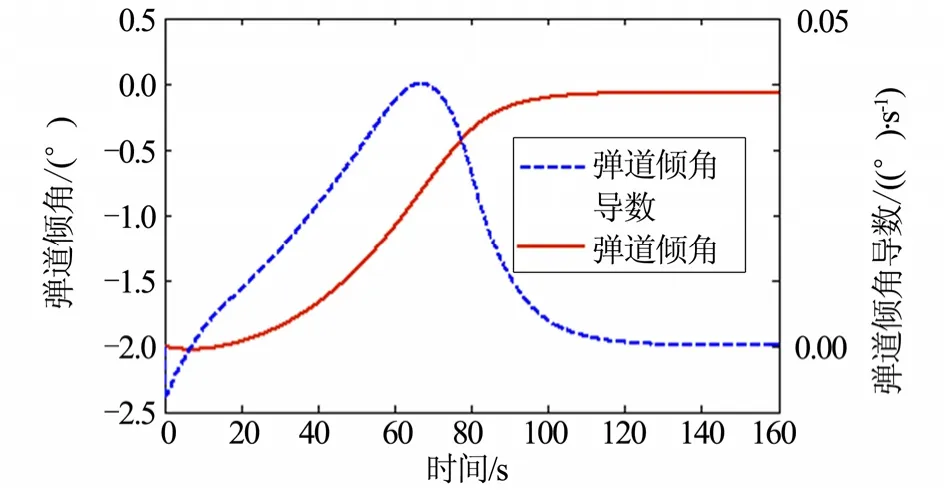
圖7 彈道傾角及其導數曲線Fig.7 Curves ofγand its First Derivative

結果表明，再入飛行器能夠平滑地進入擬平衡滑翔狀態，彈道傾角由初始值過渡到零附近的過程連續且二階可導，一階導數絕對值不超過0.05 (°)/s。

3.2 不同攻角剖面方案的光滑性對比

采用式（11）中的目標函數f作為控制量曲線的光滑性能指標，對單波峰、分段線性、分段常值3種攻角剖面進行光滑性對比，見圖8和表1。

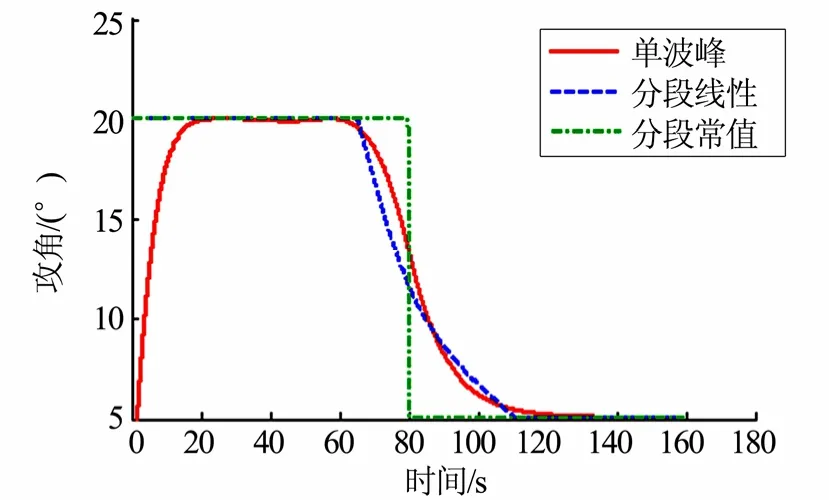
圖8 攻角曲線對比Fig.8 Comparision of Diffierent AOA Curves

表1 不同攻角剖面方案的光滑性對比Tab.1 Comparison of Smoothness with Diffierent AOA Profiles

結果表明，復合三角函數提高了攻角剖面的光滑性，使得曲線在分段過渡點處保持了較好的連續性。即使不對參數進行優化，單波峰攻角剖面相比另外兩者有先天性的光滑性優勢。此外，以上 3種剖面參數化方法的參數數量是相同的（均為3個），因此在軌跡優化時的復雜度基本一致。

3.3 不同攻角剖面方案的軌跡特性對比

為了檢驗單波峰攻角方案的優越性，將仿真結果與 Harpold[3]分段線性攻角方案、周浩[4]分段常值攻角方案得到的軌跡進行對比。采用胡錦川[7]提出的性能指標來評價軌跡平滑性：

式中 aε為縱向加速度，aε=V γ˙；tf為積分時間，tf=160 s。檢查最大過載 nmax、峰值熱流 Q˙max、過渡點動壓q等軌跡特性，見表2。

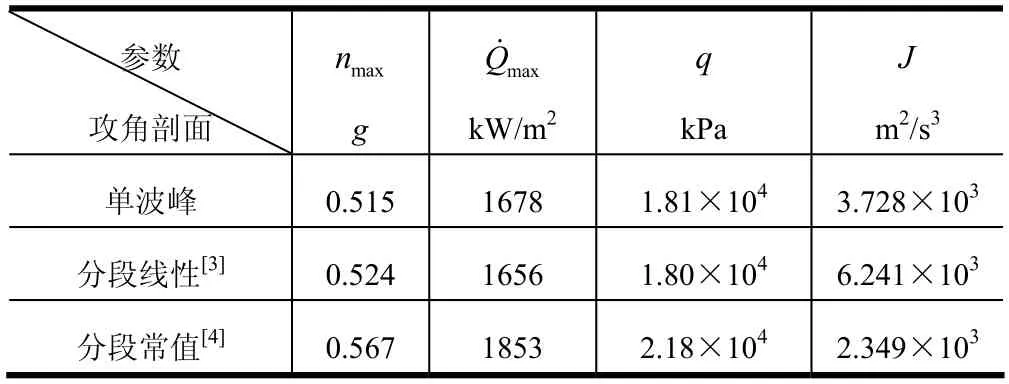
表2 3種攻角剖面的軌跡特性對比Tab.2 Comparison of Trajectory Characteristics with Three Diffierent AOA Profiles

結果表明，經過優化的單波峰攻角剖面得到的軌跡最平滑，其他軌跡性能指標與Harpold[3]攻角方案差別不大，而分段常值攻角剖面的軌跡特性最差。分析可知，分段線性攻角方案在α-t和α-V剖面均連續但不可導，導致軌跡的平滑性在過渡點處下降，而分段常值攻角方案難以保證軌跡平滑，無法滿足再入軌跡精細化設計的任務需求。

4 結束語

本文通過引入新的基函數，對原有控制量剖面進行了改進。新方法在保證參數數量不增加的情況下改善了控制量剖面的光滑性，基本滿足胡錦川[7]、張冉[8]對控制量曲線的光滑性要求。通過差分進化算法對基函數進行參數優化，使得過渡點處的攻角曲線光滑性較好，提高了軌跡平滑性，下降段的熱流、過載等環境也有一定程度改善。

復合三角函數具有在前、后端平緩變化的特點，適合在高速、大動壓情況下控制飛行器的姿態角，可以在其他場景中加以進一步的應用。

[1] 水尊師, 周軍, 葛致磊. 基于高斯偽譜方法的再入飛行器預測校正制導方法研究[J]. 宇航學報, 2011, 32(6)： 1249-1255.

Shui Zunshi, Zhou Jun, Ge Zhi-lei. On-line predictor-corrector reentry guidance law based on gauss pseudospectral method[J]. Journal of Astronautics, 2011, 32(6)： 1249-1255.

[2] 肖紅, 王勇, 國海峰, 王征, 臧旭. 基于航路點的高超聲速飛行器預測校正制導律設計[J]. 電光與控制, 2013, 20(10)： 33-37.

Xiao Hong, Wang Yong, Guo Haifeng, Wang Zheng, Zang Xu. Design of waypoint based predictor-corrector guidance law for hypersonic vehicles[J]. Electronics Optics＆Control, 2013, 20(10)： 33-37.

[3] Harpold J C, Graves C A. Shuttle entry guidance[J]. The Journal of the Astronautical Sciences, 1979, 37(3)： 239-268.

[4] 周浩, 陳萬春, 殷興良. 高超聲速飛行器多段彈道優化設計[J]. 宇航學報, 2008, 29(4)： 1205-1209.

Zhou Hao, Chen Wanchun, Yin Xingliang. Multi-phase trajectory optimization for a hypersonic vehicle[J]. Journal of Astronautics, 2008,29(4)： 1205-1209.

[5] 李強. 高超聲速滑翔飛行器再入制導控制技術研究[D]. 北京： 北京理工大學, 2015.

Li Qiang. Study on reentry guidance and control method for hypersonic glide vehicle[D]. Beijing： Beijing Institute of Technology, 2015.

[6] 劉運鵬, 李伶. 高超聲速導彈高空再入減速段彈道優化設計[J]. 航天控制, 2010.11, 28(6)： 3-6.

Liu Yunpeng, Li Ling. The optimization design for high-altitude reentry deceleration trajectory of hypersonic missile[J]. Aerospace Control, 2010,28(6)： 3-6.

[7] 胡錦川, 陳萬春. 高超聲速飛行器平穩滑翔彈道設計方法[J]. 北京航空航天大學學報, 2015, 41(8)： 1464-1475.

Hu Jinchuan, Chen Wanchun. Steady glide trajectory planning method for hypersonic reentry vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8)： 1464-1475.

[8] 張冉, 李惠峰. 基于平衡滑翔的升力再入攻角設計分析及應用[J].宇航學報, 2012, 33(11)： 1557-1563.

Zhang Ran, Li Huifeng. Angle of attack operation zone analysis and application based on equilibrium glide condition for lifting reentry[J].Journal of Astronautics, 2012, 33(11)： 1557-1563.

[9] Vinh N X, Busemann A, et al. Hypersonic and planetary entry flight mechanics[M]. Ann Arbor MI： Univ of Michigan Press, 1980.

[10] Zhang K, Chen W. Reentry vehicle constrained trajectory optimization[R]. AIAA-2011-2231, 2011.

[11] Storn R, Price K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11 (4)： 341-359.