大直徑管端定徑工藝關鍵參數與仿真研究★

焦 悅， 陳 峰， 魏長傳， 黃維勇

（1.中國重型機械研究院股份公司， 陜西 西安 710032； 2.核興航材（天津）科技有限公司， 天津東麗 300300）

對于Ф800 mm以上大直徑無縫鋼管的生產，在沒有新工藝出現的現狀下，采用熱軋（熱擴）、擠壓或擴旋工藝，都不可避免的遇到管材端部尺寸精度難以控制的問題[1]。為了達到管材端部尺寸精度要求，達到使用目的，頭尾切除成為目前唯一的方法。頭尾切除方案一是帶來極為嚴重的金屬損失，二是低下的工作效率成為影響生產線產能提高的瓶頸，因此研發一種能夠避免頭尾切除或者最短長度的頭尾切除的管端定徑裝備成為迫切。

中國重型機械研究院股份公司通過對不同D/S比值鋼管的端部定徑彈復、塑變、回彈特性的研究，采用分段組合模具，內外同時定徑的方法對管材端部進行橢圓程度的糾正和尺寸精度的提高，填補了國家空白[2]。該方案無需對管材施加縱向推力，將管材端部自由的伸入組合式分段內外模具所圍成的空腔中，通過內外模的收縮與擴張，達到大直徑管材端部尺寸要素的精確加工。目前已設計出國內首套大直徑無縫管材端部定徑裝備。該裝備可對Ф586～Ф 1 500 mm大直徑無縫鋼管的端部進行定徑，定徑后的管材橢圓度不大于管材直徑的0.25%。方案的成功應用，為進一步設計更大直徑的管材端部定徑裝備奠定了技術基礎；完善了擴旋法生產大直徑特殊用途管材的生產工藝。為了加快管端定徑裝備系列化設計，促進定徑過程中金屬變形工藝的優化。開發過程中對定徑力與被定徑管材的屈服極限、原始橢圓程度的量化關系、變形過程中與定徑精度有關的因素進行了研究，并進行了初步的仿真驗證，對于進一步完善大直徑管材的生產工藝提供了理論支撐。

1 大直徑管端定徑機的基本結構

如圖1所示，序號3為被定徑鋼管，當外模缸10的無桿腔充油后，外模缸10的活塞桿推動后梁12移動進而帶動前梁6移動，前梁6移動的同時帶動外模1圍成的圓周開始收縮，達到對鋼管外圓定徑（縮徑）的目的。內模缸9的有桿腔充油后，內模缸活塞桿拉動使內模2擴大，達到對鋼管內徑定徑（擴徑）的目的。

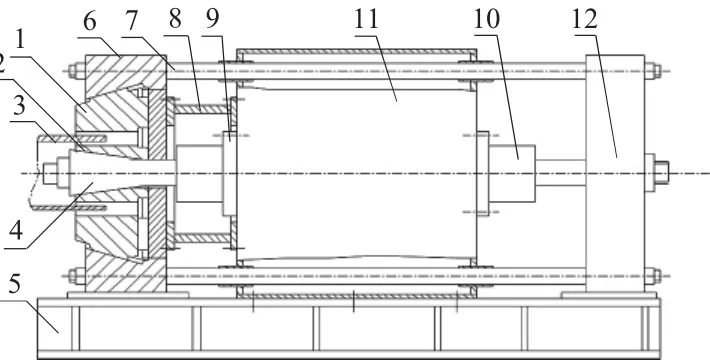
圖1 管端定徑機主機

2 擴縮徑力與主缸力參數的關系

對外模與前梁進行受力分析。取拉桿（圖1中的序號7）對前梁（圖1中的序號6）的總拉力為F1，前梁受外模的支持力為N1，前梁與外模（圖1中的序號1）的摩擦力為f1，過渡件（圖1中的序號8）對外模組支持力為N2，過渡件與外模組摩擦力為f2，取單個模具所需最大縮徑力為F。取外模與前梁接觸面的摩擦系數為μ，前梁的斜面角度為α。力學模型如圖2與3所示。

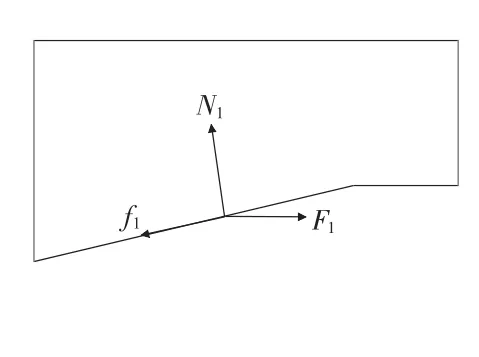
圖2 前梁受力示意圖

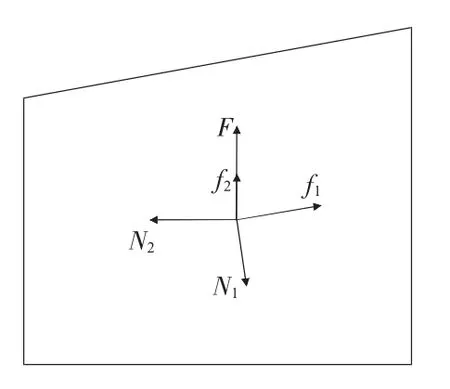
圖3 外模組受力示意圖

根據圖2，圖3受力圖，通過正交分解得以下受力關系[3]：

1）外模：

2）前梁：

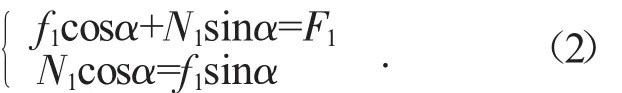
由式（1）與式（2）可解得，液壓缸需要提供的最大推力Fmax為：

式（3）中F′為變形后的縮徑力。根據方案初步確定的設計數據，取 α=10°，μ=0.1，帶入式（3），可得：

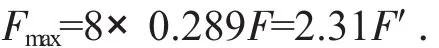
通過對外模縮徑力的分析可知，內模擴徑力與液壓缸受力的分析路徑相同，不在贅述。內模與活塞桿之間的斜面角度與外模和前梁之間的斜面角度相同，接觸面之間的摩擦系數也相同，通過與上述過程相同的計算得知，內模液壓缸的最大拉力Fmax=8×0.289F=2.31F′。

3 不同規格管材擴徑與縮徑力的確定

為了便于計算，根據內模的結構實際，計算時主要考慮變形區大小和擴徑段壁厚因素的擴徑力計算公式為[4]：

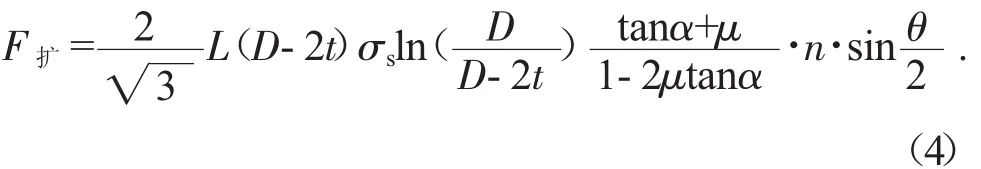
式中：α為斜面角；θ為單個模具對應的分度角；L為擴徑段長度；t為管材壁厚；D為擴徑后的外徑數值；σs為管材材質屈服強度；μ為摩擦系數。

根據外模外圓直徑偏大，模具數量分組較多的因素，其縮徑力的計算公式為[5]：

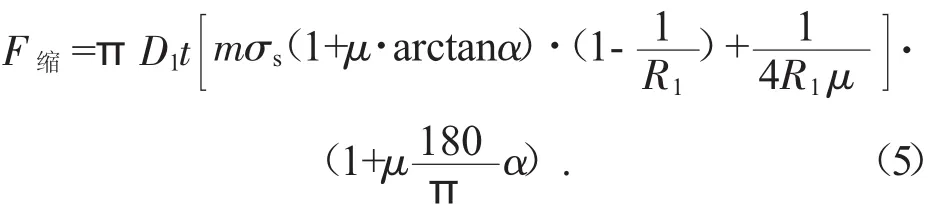
式中：D1為縮徑后的外徑數值；m為經驗系數在2.3～2.5之間；μ為摩擦系數；σs為管材材質屈服強度；R1為縮徑后的管材外圓半徑。

上述計算方法沒有考慮變形程度和變形剛端的問題。按照目前的工程經驗,考慮變形程度和變形剛端影響的因素不足以產生過多的影響。在實際生產中，按照公式（5）計算的理論數值和實測差值約在10%～15%，從工程角度來講，可以滿足理論指導作用。

4 擴、縮徑量與定徑目標值的關系

研究定徑后橢圓精度目標與定徑過程中的擴、縮徑的變形量之間的關系，從而對實際生產過程中的變形工藝參數進行量化指導，是研究管端定徑工藝的關鍵所在。對此問題，研究思路是建立在理論公式的推演和計算機模擬仿真之上，結合生產實測實際，最終獲得適應于工程計算的擴徑（縮徑）量指導公式。

擴徑和縮徑的工藝特點是：在擴縮徑過程中，由于彈性變形的存在，在擴縮徑結束后會有一定的彈性回彈，所以在擴縮徑之前要通過計算得出理論擴縮徑量。根據現有的文獻資料，可以推演得到擴徑理論值計算過程如下[6]：

模具的歸園量S1可以表示為：（不考慮彈性變形和壁厚變化的公式）

式中：Rm0為鋼管的平均半徑；b為鋼管中性層的橢圓短軸半徑。

模具的擴徑量實際上與名義擴徑率、鋼管壁厚變化有關，考慮到這些因素，將變化因素的擴徑量記作 S2，則：

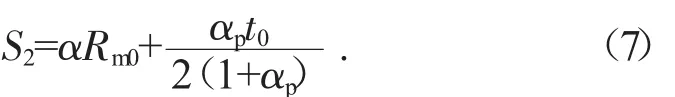
式中：α 為名義擴徑率，α=αp+αe，αe為塑性擴徑率，αp為彈性擴徑率；t0為圓管初始厚度。

式中：σs為屈服強度；E為彈性模量；δ′為相對壁厚

理論上的擴徑量為：

根據以上推演公式，以理論直徑1 500 mm、短軸1 430 mm、長軸1 480 mm、壁厚60 mm的圓管為例。代入公式（9）得：S=38.14 mm；若不考慮彈性變形，則S=35 mm。

將管材沿周向分成20個點，用FORGE軟件模擬各個點在兩種擴徑量條件下定徑后的橢圓程度（見表 1）。

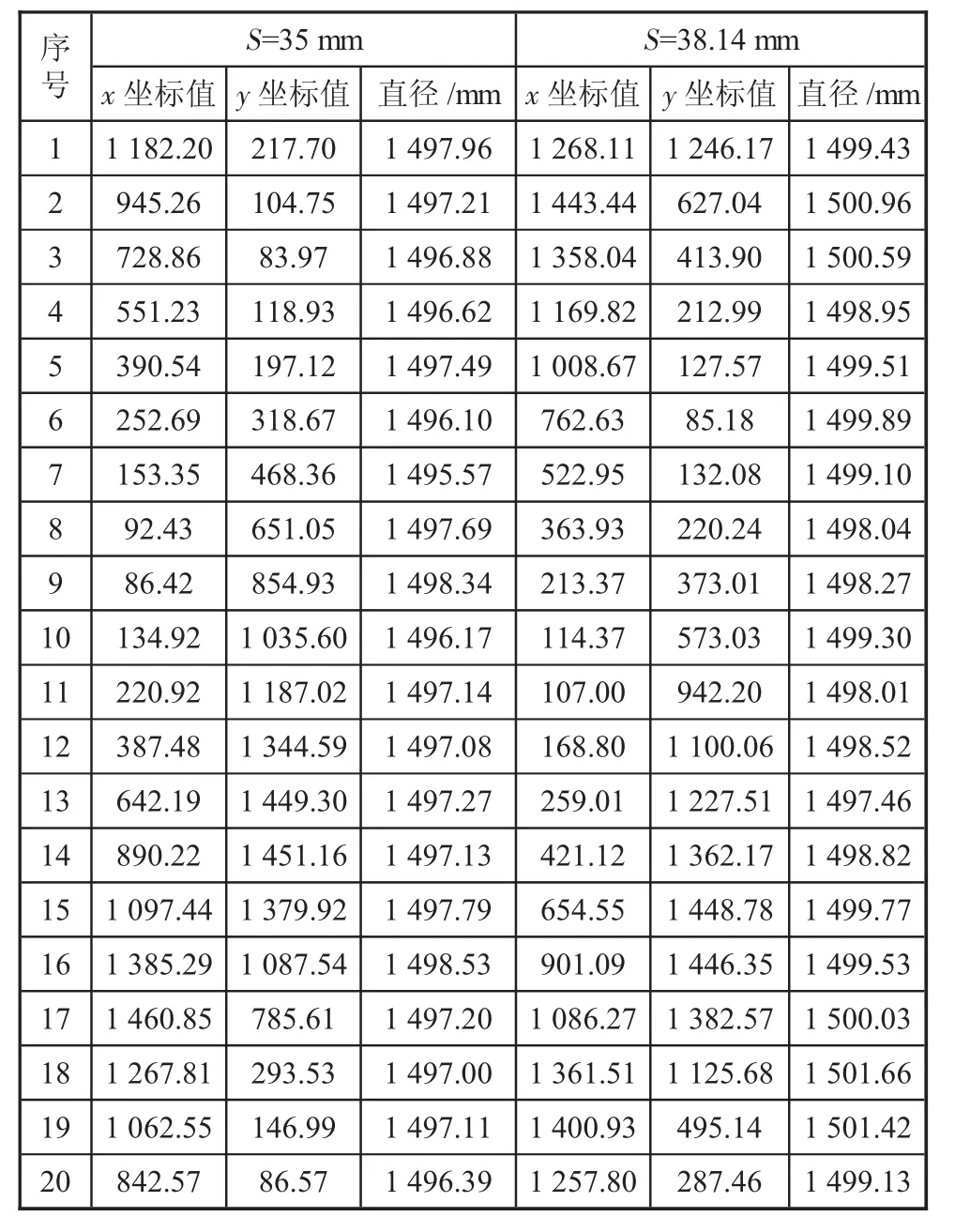
表1 不同擴徑量的結果對比

由表1可知：當按照35 mm的擴徑量時，最大直徑為1 498.53 mm，最小直徑為1 495.57 mm；當按照38.14 mm的擴徑量時，最大直徑為1 501.66 mm，最小直徑為1 498.01 mm；前者的橢圓度為2.96 mm，后者為3.65 mm。可以印證，在擴徑工藝過程中，不考慮彈性因素的擴徑量選擇較為切合工程實際。

機械縮徑時，縮徑量被定義為縮徑模具在管坯長軸方向的徑向位移。該參數由理論圓數值和縮徑圓數值兩部分構成，前者取決于管端的原始橢圓度，后者取決于管端的名義縮徑率。

1）歸圓量。

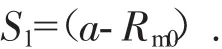
式中：a為鋼管中心層橢圓長軸半徑；Rm0為圓管的平均半徑；b為圓管中性層的橢圓短軸半徑。

在標準橢圓上，橢圓度誤差為：

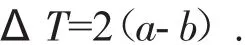
2）縮徑量。

模具的縮徑量與名義縮徑率、管端壁厚變化有關。若將其記作S2，則：

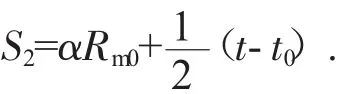
式中：α 為名義縮徑率，α=αp+αe，αe為塑性縮徑率，αp為彈性縮徑率；t0為管端初始厚度；t為管端縮徑后厚度。

總行程為：

根據以上理論公式，以理論直徑1 500 mm，長軸1 540 mm，短軸1 490 mm，壁厚60 mm的橢圓鋼管為例。代入以上公式進行計算可得：S=22.87 mm；若不考慮彈性變形，則S=20 mm。同樣將管材沿周向分成30個點，用FORGE軟件進行模擬各個點在兩種縮徑量條件下橢圓程度。選取30個點的目的是，精整的精度最終影響過程在于縮徑過程（見表2）。

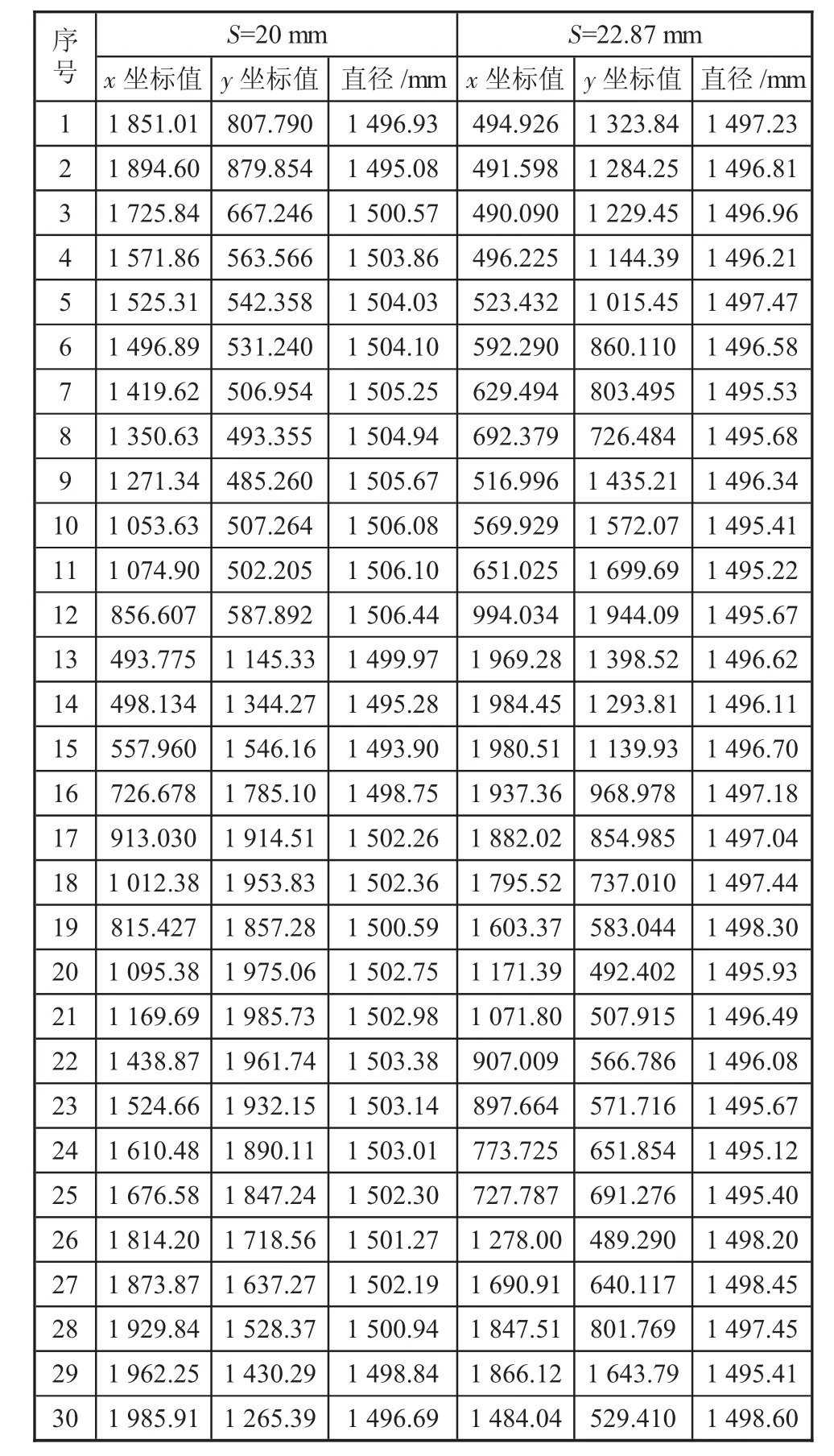
表2 不同縮徑量的結果對比

由表2可知：當按照20 mm的縮徑量時，最大直徑為1 506.44 mm，最小直徑為1 493.90 mm；當按照22.87 mm的縮徑量時，最大直徑為1 498.6 mm，最小直徑為1 495.12 mm；橢圓度分別為12.54 mm和3.84 mm。可見縮徑過程中的彈性回彈的影響要大于擴徑過程。

實際上在上述研究的過程中忽略了一個問題，也就是定徑模具數量的問題，定徑模具數量也會影響到定徑的橢圓程度，這是研究大直徑管材端部定徑精度不可忽視的問題。當管端直徑達到1 000 mm以上時，在各組模具的結合部位，管材無論是擴徑或縮徑過程，都會形成一個較為自由的部位，這個自由部位的大小成為會影響管材定徑后的橢圓精度的關鍵。本研究過程中對理論直徑為1 500 mm管材端部定徑模具的分組數量與定徑精度驚醒了仿真模擬。當定徑模具沿圓周方向的數量從7組到12組加密的過程中橢圓數值越來越小，單個模具的端面接觸應力越來越大，對模具本身的機械性能就越高。對直徑1 500 mm左右，壁厚不大于60 mm的管端，10組模具的分組已經完全滿足工程需要。

5 結語

從工程實踐的角度對大直徑管材端部定徑的關鍵參數進行了推演計算，并對影響定徑效果的兩個最關鍵參數擴縮徑量以及模具分組數量進行了量化確定。研究成果對于大直徑管材端部定徑工藝設定提供了理論支撐，對大直徑管材端部定徑裝備的結構參數優化提供了直接依據。

[1]許小華，陳俊德.大口徑熱擴無縫鋼管的發展與應用[J].材料導報網刊，2010（1）：13-15.

[2]陳峰，屈薛勇.大直徑無縫鋼管的端部定徑裝置[J].焊管，2018，41（2）：46-49.

[3]梁治明.材料力學[M].北京：人民教育出版社，1963.

[4]黃克堅，蘇章卓.焊管機械擴徑力的計算[J].焊管，2010（12）：23-26.

[5]鄭素梅，矯慶春.SJ194縮徑機的研制及機[J].焊管，1998（1）：29-31.