微潤管埋深及壓力水頭對青椒生長和水分利用的影響

雷　濤，畢遠杰，雷明杰，張少文，孫西歡,3，馬娟娟，郭向紅

(1.太原理工大學 水利科學與工程學院，太原　030024；2.山西水利水電科學研究院，太原　030024；3.晉中學院，山西 晉中　030060)

0　引言

微潤灌溉是一種新型的地下連續灌溉技術[1-2]，埋藏于土壤耕作層的微潤管利用滲透膜原理，將水分緩慢釋放于管帶周圍的土壤中，水分能夠直接抵達根系集中層[3]。該灌水技術具有棵間蒸發小、水分利用率高及促進作物增產等諸多優點，多年來得到了廣泛應用和發展[4]。在我國，糧食安全是關系到國計民生的頭等大事，它直接牽涉到經濟發展及國家穩定的大局[5]。因此，開展微潤灌條件下作物生長和產量方面的研究，對于制定科學合理的灌溉方法及田間工程布置方案有著重要的指導作用和意義。

目前，微潤灌方面的報道已經很多，主要包括濕潤體內水鹽運移分布[6-7]、微潤管水力性能[8-9]、管路堵塞原因[10]及作物生長特性及產量[11-16]等方面。關于作物生長和產量方面，相關報道主要集中在作物生長特性及產量對埋深、壓力水頭的響應方面。張子卓[11-12]指出：在不同的壓力水頭和埋深組合條件下，番茄生長和水分利用情況并不相同。這說明，兩個試驗因素之間可能存在耦合效應，但該研究并未對其耦合效應進行揭示。通常情況下，當植株長勢越好、產量和水分利用效率越高時，說明該灌水條件越優。關于番茄、向日葵、棗樹、青椒的最優灌溉條件已有相關報道，其中指出：番茄的最優灌溉條件為水頭1.8m和管帶埋深15cm[11-12]，或者水頭1.2～1.7m和微潤管埋深10cm[12]；向日葵和棗樹的最優灌溉條件為管帶埋深20cm和30cm[14-15]。對于前面提到的這幾種作物，當達到最優灌溉條件時，能同時滿足長勢最好、產量和水分利用效率最高；但對于青椒而言，結果略有不同。雷明杰[16]等人指出：當壓力水頭為150cm時，青椒株高和產量達到最大；而在壓力水頭為100cm時，水分利用效率最高。目前，關于番茄、向日葵、棗樹、青椒的最優灌溉條件已有報道，但也存在一定的不足。目前，這些研究多偏重于單因素對作物生理特性的影響，壓力水頭和管帶埋深兩個因素間的耦合效應對作物莖粗、株高、產量和水分利用效率的影響尚不清楚，還有待進一步研究。有報道指出：作物的生長過程基本符合S形變化趨勢[11]，可采用經典的logistic模型進行描述[16]；但該模型中并未考慮水頭、埋深及其交互效應的影響，還有待進一步改進。

本文旨在于揭示不同壓力水頭、管帶埋深及其交互效應對青椒生長特性、產量和水分利用效率的影響，確定最優的壓力水頭和管帶埋深，并建立相應的數學定量模型，以期為微潤灌溉技術的完善提供有力支持，為農業生產實際提供指導。

1　材料與方法

1.1　試驗地基本情況

試驗于2016年4-9月在山西水利水電科學研究院節水高效示范基地日光溫室內進行。試驗地年平均氣溫9.6℃，年平均日照時數2 675.8h，年降水量495mm。試驗土壤為粘壤土，土壤平均容重為1.39g/cm3，田間持水率為0.35cm3/cm3。

1.2　試驗材料與設計

本試驗進行不同灌溉埋深及壓力水頭條件下青椒生長特性研究，試驗方案如表1所示。其中，壓力水頭分別設置100、150、200cm等3個水平，管帶埋深設置10、15、20cm等3個水平。本文采用全面試驗設計，共9組處理，每個處理設3組重復。供試青椒品種為高思頓凱璐，行株距為60cm×60cm。定植時間為2016年4月12日，結束時間為2016年9月22日。青椒種植于微潤帶正上方，在青椒整個生育期內連續供水。

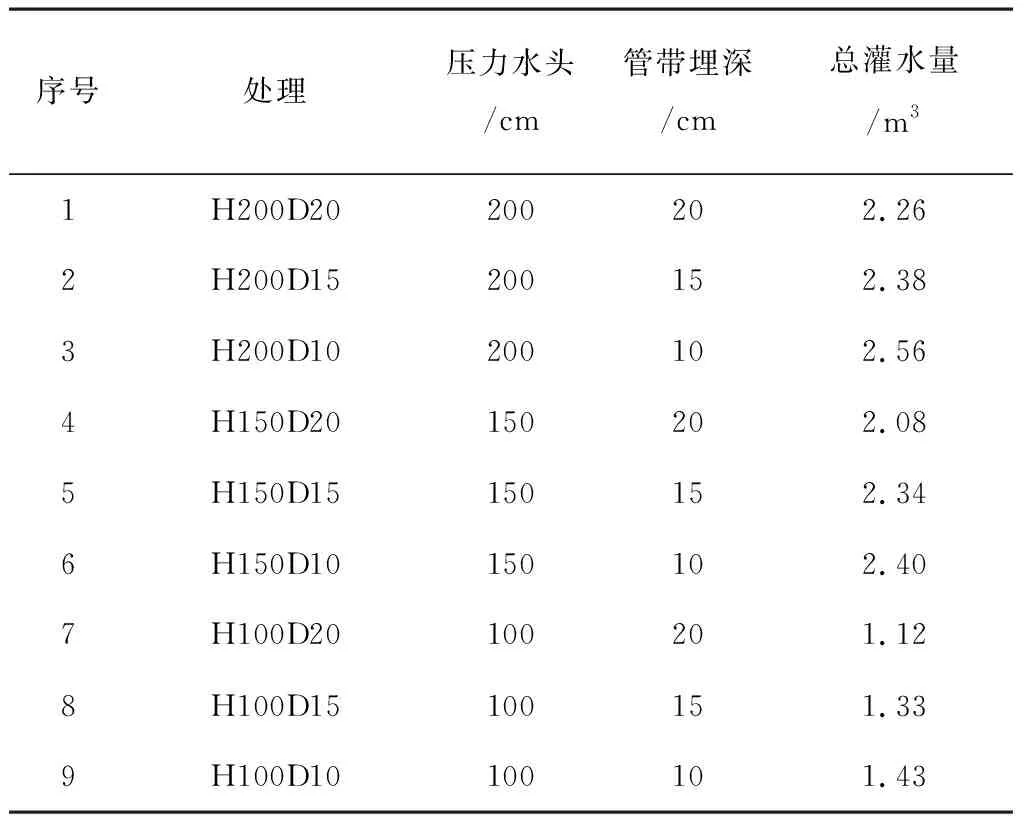
表1　試驗設計

1.3　數據測試方法

1)株高測定：每10天、每個處理任選3株樣本，采用鋼卷尺對其株高進行測定，取均值。

2)產量測定：定植83天后，采用精度為0.01g的電子天平，定期對各處理的青椒進行稱重，取重復組的平均值作為各處理的測定值。

3)莖粗測定：采用游標卡尺對青椒基部距地面1cm位置處進行測定，作為測定值。

1.4　數據處理

由于不同管帶埋深和壓力水頭處理下青椒生長指標的動態變化符合S型變化趨勢，因此本文采用logistic模型進行定量描述，即

(1)

其中，Y為青椒莖粗或株高(cm)；F為莖粗常數尺度或株高常數尺度(cm)；C為莖粗極大值或株高極大值(cm)；K為莖粗相對生長速率參數或株高相對生長速率參數(cm)；t為累積生長時間(天)。

采用Microsoft Office 2013軟件進行數據處理，采用IBM SPSS Statistics 19軟件進行統計學分析，采用Origin 9.0繪圖。采用平均相對誤差MAPE對模型精度進行評價，即

(2)

其中，WL為青椒生長指標預測值(cm)或者產量預測值(kg/hm2)，WR為青椒生長指標實測值(cm)或者產量實測值(kg/hm2)；N為樣本數。

2　結果分析

2.1　管帶埋深與壓力水頭對莖粗和株高的影響

圖1為不同管帶埋深與壓力水頭條件下青椒莖粗動態變化過程。

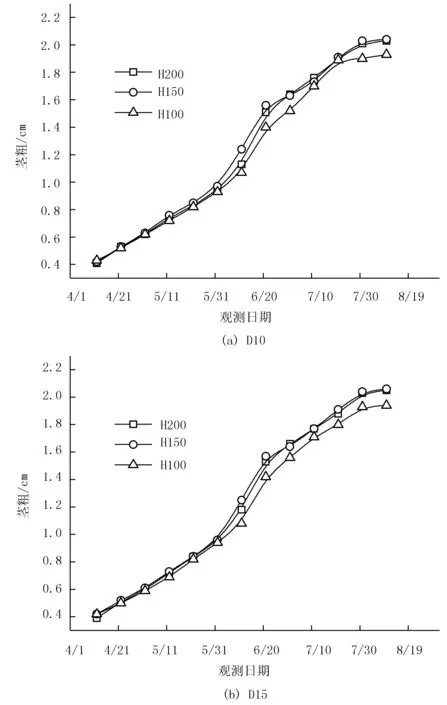
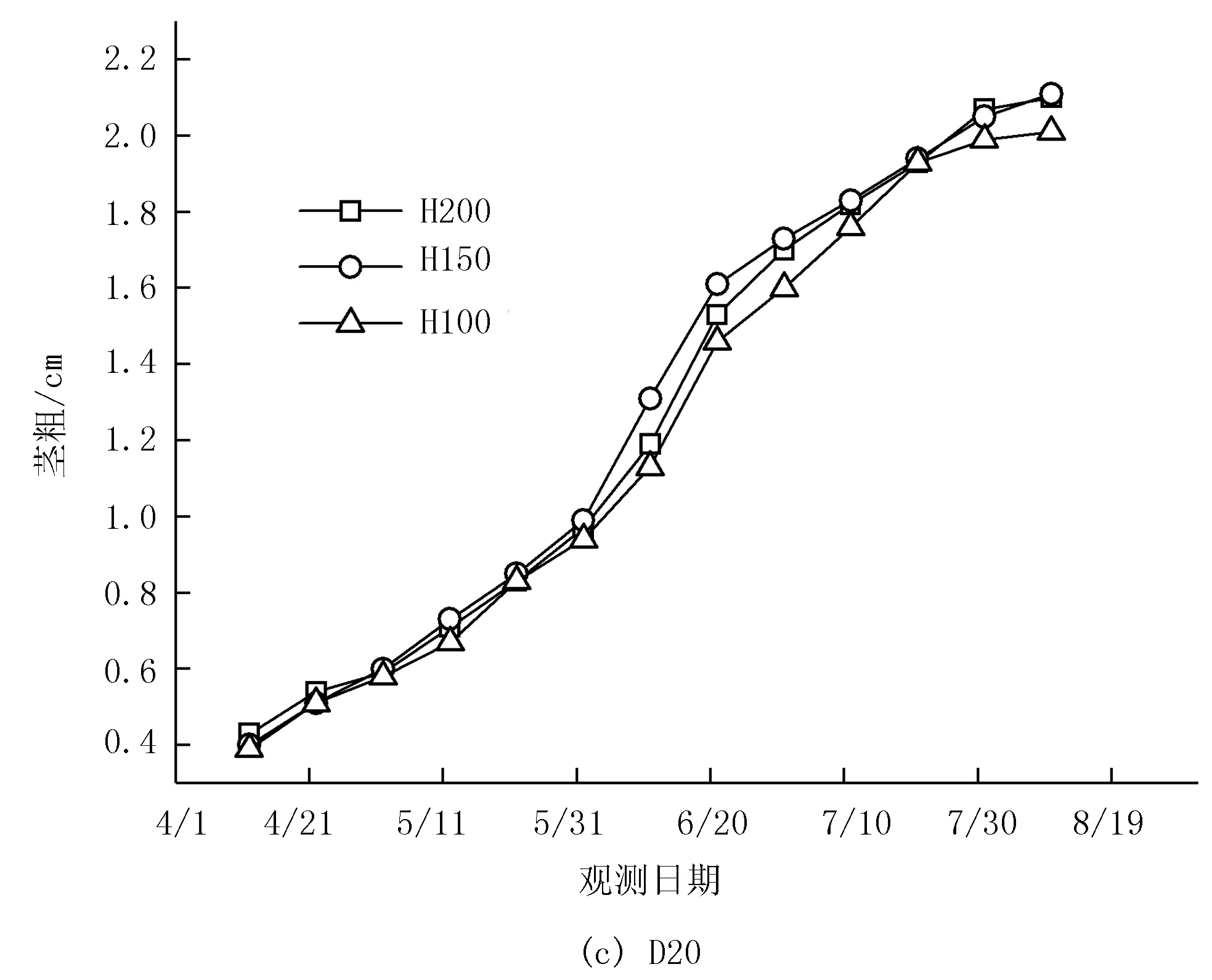
圖1　不同管帶埋深與壓力水頭條件下青椒莖粗動態變化過程

由圖1可知：不同管帶埋深及壓力水頭處理后的青椒莖粗均隨時間呈現S形變化趨勢。也就是說，先緩慢增加，然后快速增加，最后緩慢增加并趨于穩定。由圖1可知：經D10和D15處理后的青椒莖粗無明顯差異。經D20處理后的青椒莖粗要明顯大于D10處理和D15處理。由此可以說明，管帶埋深的增加有利于青椒生長。由圖1可知：在管帶埋深10cm與15cm時，H150與H200處理后的青椒莖粗基本接近，在數值上要明顯大于H100處理；在埋深20cm時，3種壓力水頭處理后的莖粗差異較為明顯，3種處理效果表現為H150>H200>H100。配對t檢驗結果表明：任意兩個壓力水頭處理間的莖粗差異均能夠達到顯著(p<0.05)或者極顯著(p<0.01)水平。除D15與D20兩種埋深處理后的莖粗差異能夠達到顯著水平外，其余各個埋深處理后的莖粗均無統計學差異。

圖2為不同管帶埋深與壓力水頭條件下青椒株高動態變化過程。由圖2可以看出：不同管帶埋深及壓力水頭處理后的青椒株高均隨時間呈現先緩慢增加，然后快速增加，最終緩慢增加并趨于穩定的變化趨勢，基本符合S形變化趨勢。由圖2可以看出：經D10和D15處理后的青椒株高大小較為接近，無明顯差異；經D20處理后的青椒株高要明顯大于D10處理和D15處理。由此可以說明，管帶埋深的增加有利于青椒生長。由圖2可以看出： 在管帶埋深10cm與15cm時，H150與H200處理后的青椒株高基本接近，在數值上要明顯大于H100處理；在埋深20cm時，H200與H150處理后的青椒株高基本接近，在數值上要明顯大于H100處理。由此可以說明，適當的增加壓力水頭將有利于株高的增加。采用t配對檢驗方法，對各個處理后的株高數據樣本進行了分析，結果表明：除D10與D15處理后的株高差異不顯著外，其余任意埋深處理后株高差異均達到顯著水平。

圖2　不同管帶埋深與壓力水頭條件下青椒株高動態變化過程

2.2　管帶埋深與壓力水頭耦合條件下青椒莖粗、株高生長模型

結合圖1和圖2可以看出：青椒的莖粗和株高的動態變化過程較符合S型變化趨勢。因此，采用式(2)對莖粗和株高進行了定量描述。經計算，各個單因素處理下的莖粗和株高定量模型的決定系數分別為0.986～0.991和0.983～0.993，說明logistic模型能夠準確描述莖粗和株高的動態變化過程。但是，傳統的logistic模型中并未考慮壓力水頭和埋深的影響，有必要做進一步的改進。因此，本文的關鍵在于構建生長速率的修正函數，建立埋深、壓力水頭與莖粗生長速率之間的定量關系，以及建立這兩個因素和株高生長速率間的定量關系，即

(3)

其中，K(D,H)為生長速率的修正函數。

圖3為不同壓力水頭和埋深處理后的莖粗生長速率Kjc和株高生長速率Kzg。由圖3可以看出：當壓力水頭由H100增長到H200時，Kjc和Kzg均呈現冪函數形遞增的變化趨勢，兩者在數值上會分別增加7.17%～15.96%和5.12%～8.47%；相對D10處理而言，在D20條件下，Kjc和Kzg對壓力水頭的響應更強。由圖3還可以看出：當管帶埋深由D10增加到D20時，Kjc和Kzg均呈現冪函數型增長的變化趨勢，兩者在數值上會分別增加11.98%～21.59%和2.98%～6.26%，并且相對H100處理而言，在H200條件下，Kjc

和Kzg對管帶埋深的響應更強。由以上分析可以看出，管帶埋深和壓力水頭可能對Kjc和Kzg存在交互效應。因此，進一步對數據樣本進行了雙因素方差分析，結果如表2所示。由表2可以看出：管帶埋深和壓力水頭對Kjc和Kzg的影響分別達到了顯著(p<0.05)或者極顯著水平(p<0.01)，雙因素的交互效應對Kjc和Kzg影響均達到顯著水平(p<0.05)。

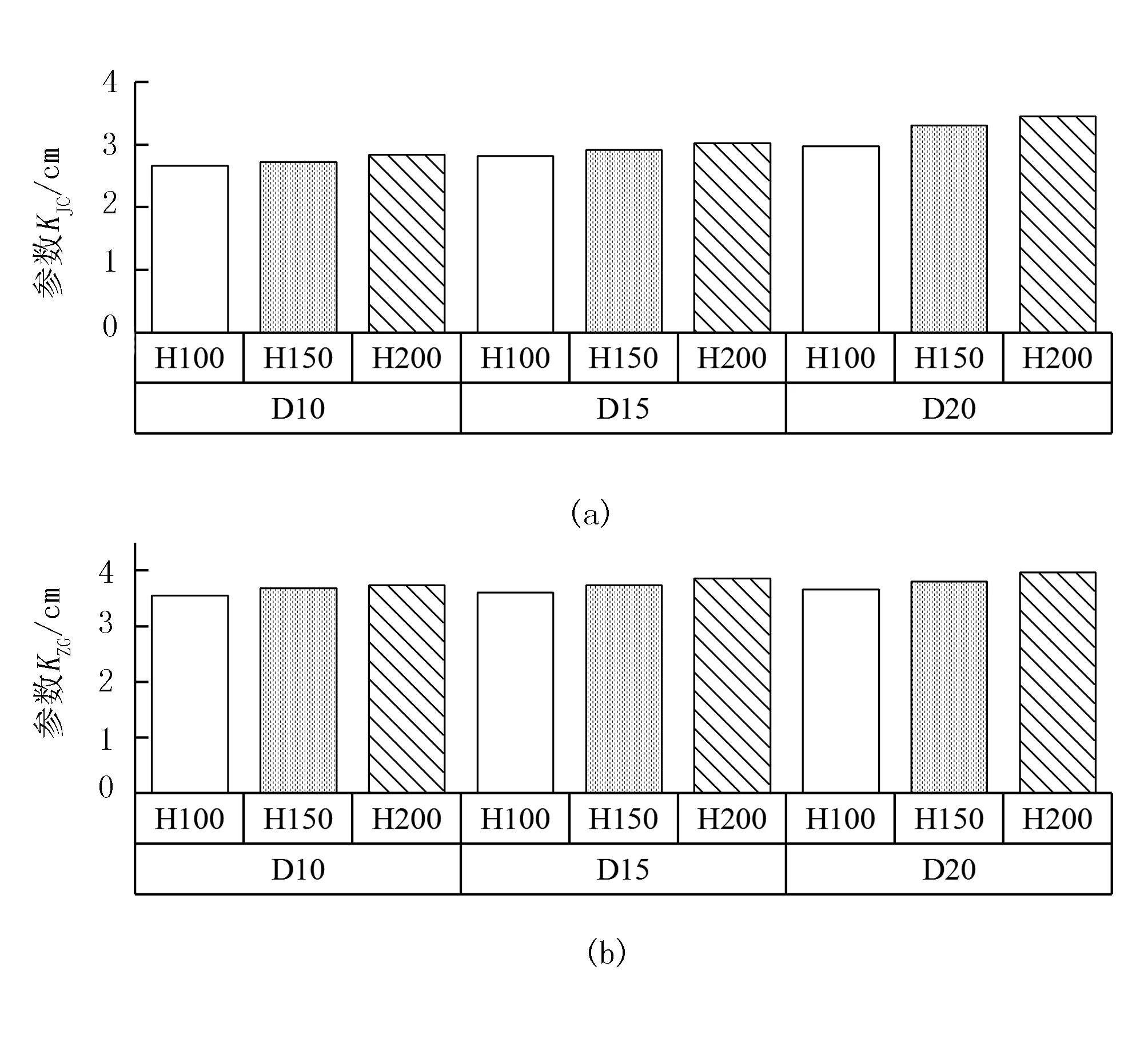
圖3　不同管帶埋深與壓力水頭對生長參數的影響

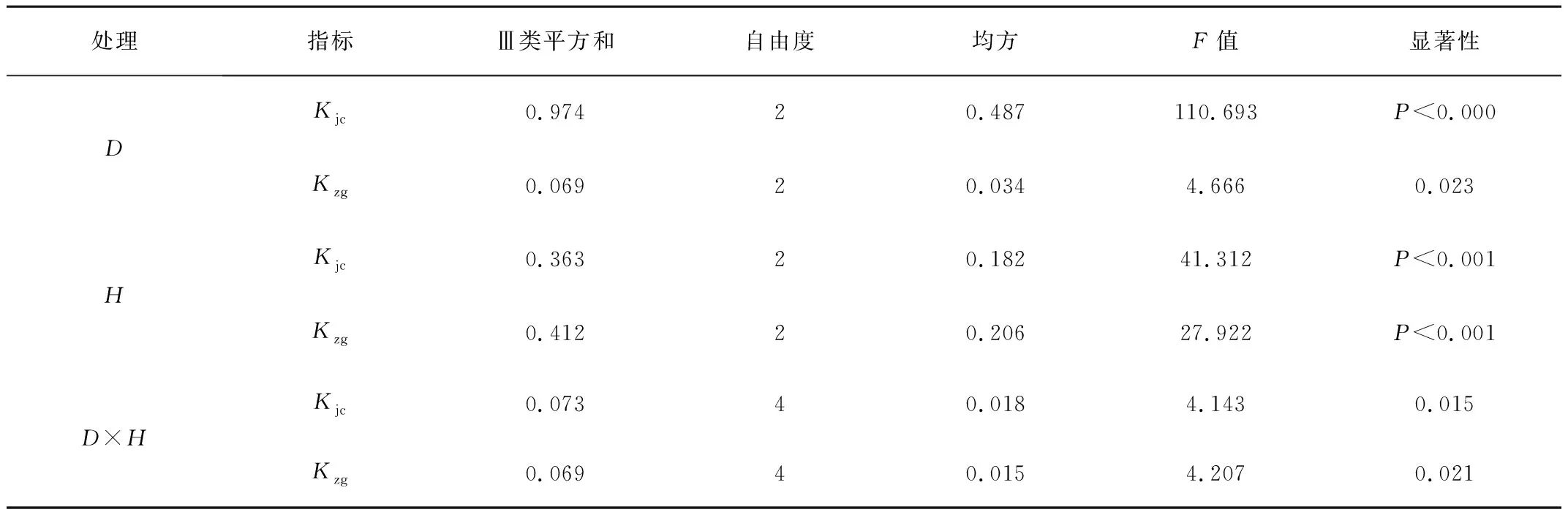
表2　青椒生長參數雙因素方差分析

由圖3可以看出：莖粗生長速率、株高生長速率與壓力水頭和埋深間的關系均符合冪函數形式。結合表2 ，管帶埋深和壓力水頭對莖粗生長速率和株高生長速率存在顯著的交互影響，因此在模型構建過程中需要考慮到交互作用的影響。根據以上兩點理由，本文所構建的莖粗生長速率Kjc和株高生長速率Kzg的修正函數如式(4)所示。當將式(4)帶入式(3)后，便可以得到壓力水頭與埋深耦合條件下的青椒莖粗生長模型DH-YJC和株高生長模型DH-YZG。分別采用各個處理后的莖粗數據和株高數據，對DH-YJC模型和DH-YZG模型的參數進行了率定，對模型精度進行了計算，結果如表3所示。由表3可知：DH-YJC和DH-YZG的平均相對誤差分別為5.25%和4.72%。這說明，兩個模型可較好地描述青椒生長過程。

K(D,H)=m·Dn·Hp

(4)

其中，m、n和p均為系數。

表3　DH-YJC模型與DH-YZG模型參數

2.3　管帶埋深與壓力水頭對青椒產量的影響

圖4為不同管帶埋深與壓力水頭對青椒產量的影響。

圖4　不同管帶埋深與壓力水頭對青椒產量的影響

由圖4可知：在H200、H150和H100水頭條件下，當埋深由D10增加到D20時，青椒產量呈增加趨勢，產量分別增加19.72%,19.04%和11.64%。這說明，青椒產量與管帶埋深呈正比。其原因是：青椒根系主要分布在地表以下10～20cm，管帶埋深10cm時，微潤灌濕潤體分布在地表附近，不利于作物根系向下生長；而管帶埋深20cm能保持青椒根系在微潤管濕潤范圍內，并誘導青椒根系深扎，為青椒的正常發育

提供良好的水分條件，利于青椒水肥的吸收，達到增產效果。由圖4還可以看出：在任意管帶埋深條件下，經H150處理后的青椒產量最高，H200處理后的產量次之，H100處理后的產量最小。這是由于當壓力水頭較低時，濕潤體范圍較小，濕潤體的位置靠近地表，這將會影響青椒根系對土壤水分的吸收；但當壓力水頭過大時，濕潤體沿垂向的分布深度會增加，根系集中層位置高于水分集中層，同樣也會影響土壤水分對根系的供應；當供水壓力處于H150水平時，濕潤體位于根系集中層，最有利于根系對水分的吸收，從而促進產量增加。

為了進一步探究管帶埋深與壓力水頭的耦合效應是否對產量存在影響，采用雙因素方差分析對數據樣本進行了分析。結果表明：埋深和壓力水頭對產量均有極顯著的影響(p<0.01)，但兩者的交互效應對產量無明顯影響(p=0.348)。由圖4可以看出：埋深、壓力水頭與產量之間的關系分別符合線性和拋物線函數。由于雙因素的交互效應對產量無影響，因此模型建立中不考慮交互效應。因此，壓力水頭與埋深耦合條件下的青椒產量模型DH-YCL如式(5)所示，模型參數及精度如表4所示。由表4可以看出：模型的決定系數和平均相對誤差分別為0.970和1.76%。這說明，本文所建立的DH-YCL模型誤差較小，可用于埋深與壓力水頭耦合條件下青椒產量的定量描述。

YCL=a+b·H2+c·H+m·D

(5)

其中，a、b、c和m為系數。

表4　DH-YCL模型參數

2.4　管帶埋深與壓力水頭對水分利用的影響

圖5 為不同管帶埋深和壓力水頭對水分利用效率的影響。由圖5可以看出:在H200、H150和H1000壓力水頭下，當管帶埋深由20cm減少到10cm時，水分利用系數會分別下降26.3%、27.3%和30.0%；在D20、D15和D10埋深下，當壓力水頭由200cm降低到100cm時，水分利用系數會分別增加67.9%、49.71%和59.5%。由此可以看出：水分利用系數與埋深呈正比，與壓力水頭呈反比。在不同的水頭和埋深組合條件下，水分利用系數對各個因素的響應強度存在差異，說明水頭和埋深兩個因素對水分利用系數可能存在一定的交互影響。為此，進一步采用雙因素方差分析方法，對兩個因素與水分利用系數之間的關系進行探究，結果表明：水頭、埋深及兩者間的耦合效應對水分利用系數的影響均達到極顯著水平(p<0.01)。由圖5還可以看出：水分利用系數與兩個因子間的關系均符合冪函數關系。由于雙因素的交互效應對產量影響顯著，因此模型建立過程中需要考慮交互效應。壓力水頭與管帶埋深耦合條件下的水分利用系數模型YXS如式(6)所示，模型參數及精度如表5所示。由表5可以看出：模型的決定系數和平均相對誤差分別為0.960和4.44%。這說明，本文所建立的DH-YXS模型誤差較小，可用于埋深與壓力水頭耦合條件下水分利用系數的定量描述。

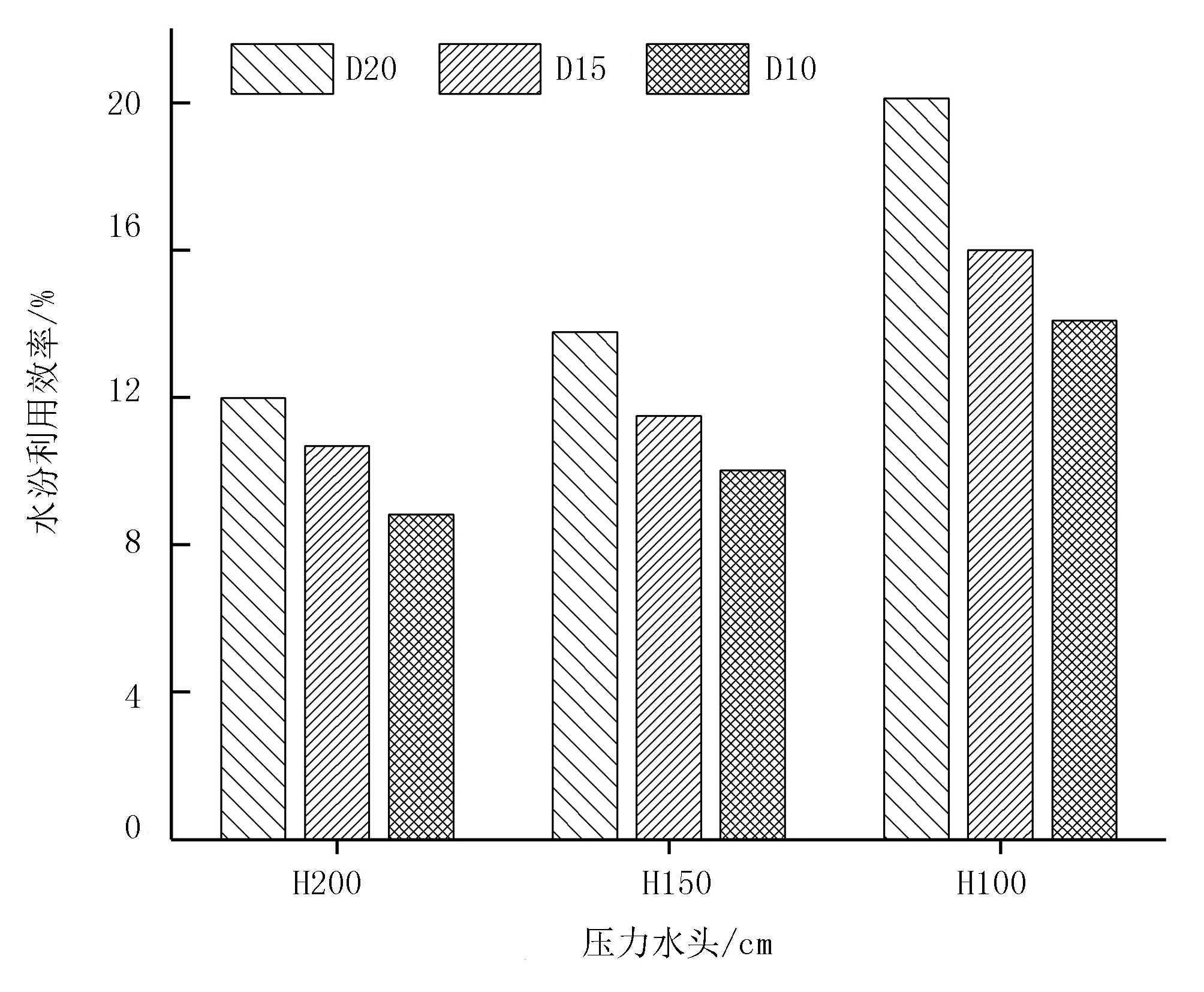
圖5　不同管帶埋深與壓力水頭對水分利用效率的影響

YXS=a·Hb·Dc

(6)

表5　DH-YCL模型參數

3　結論

1)不同管帶埋深及壓力水頭處理后的青椒莖粗和株高均隨時間呈現S形的變化趨勢。管帶埋深、壓力水頭這兩個試驗因素均與青椒莖粗、株高、莖粗生長速率和株高生長速率呈顯著的正相關。管帶埋深、壓力水頭及這兩個因素間的交互效應對莖粗生長速率、株高生長速率的影響達到極顯著水平。

2)當管帶埋深為20cm、壓力水頭為150cm時，有利于青椒生長，此時的產量最高。

3)當管帶埋深為20cm、壓力水頭為100cm時，水分的利用系數最高。

4)建立了管帶埋深與壓力水頭雙因素耦合條件下的株高生長模型DH-YZG、莖粗生長模型DH-YJC、產量模型DH-YCL和水分利用系數模型DH-YXS，這4種定量模型的平均相對誤差MAPE分別為4.72%、5.25%、1.76%和4.44%，取得了滿意的模擬效果。