(2,p)-Laplace方程的緊性條件及其應用
劉慧慧,梁占平
(山西大學 數學科學學院,太原 030006)
本文研究(2,p)-Laplace方程
(1)
我們稱u是方程(1)的解,如果u滿足
進一步,稱u是方程(1)的正解。如果u是方程(1)的解,u≠0,并且u≥0對x∈Ω成立,令
(2)
近年來,許多學者用變分方法深入研究過方程(1)以及類似問題(如(p,q)-Laplace方程解的存在性),也得到許多比較好的結果。為了得到解的存在性,大多數文獻都需要討論類似J的泛函的緊性條件[3-9]。
本文主要分為兩個部分:第一部分主要說明J的緊性條件;第二部分利用J的緊性條件得到方程(1)的正解。為方便起見,固定一些符號:對所有t∈R,t±=max(±t,0);|·|r表示Lr(Ω),r∈[1,∞)中的范數;‖·‖*表示W-1,p'(Ω)中的范數;ci(i=1,2,…),C以及Cε表示不同的正常數。
1 主要結果
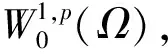
(1+‖un‖p)J'(un)→0,
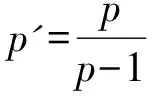
1)f∶Ω×R→R是Carathéodory函數,且f(x,0)=0對幾乎處處的x∈Ω成立。
2) |f(x,t)|≤α(x)(1+|t|p-1)對幾乎處處的x∈Ω,所有的t∈R成立;其中,α∈L∞(Ω)且α(x)>0對幾乎處處的x∈Ω成立。
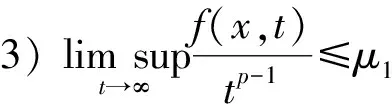
(3)
4) 存在函數η∈L∞(Ω),且η(x)>0對幾乎處處的x∈Ω成立,使得μ1≤η(x)對幾乎處處的x∈Ω成立,μ1≠η,且
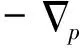
5)tf(x,t)-pF(x,t)≥0對幾乎處處的x∈Ω,所有的t≤0成立,且f(x,·)滿足對每一個緊集K?[0,∞],都可以找到ξK>0,使當t1>t2時,有
f(x,t1)-f(x,t2)≥-ξK(t1-t2) ,
對幾乎處處的x∈Ω,所有的t1,t2∈K成立。
文獻[3]證明了當f次臨界,在∞附近(p-1)-超線性,在-∞附近(p-1)-次線性時,J滿足C-條件。在文獻[9]中,若f次臨界且存在C>0,使得
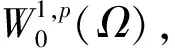
本文研究當f滿足下列條件(H)時,J的緊性條件。
(H) 對a1,a2<∞,極限
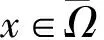
用∑p表示帶有Dirichlet邊界的p-Laplace算子的Fucik譜。具體地說,集合∑p表示使得
有非平凡解的(a,d)∈R2的全體。這里,u±=max{±u,0}.由文獻[10]易知,若(a,d)∈∑p且a,d≠μ1,則a>μ1且d>μ1.其他Fucik譜的相關性質見文獻[10-11]及其參考文獻。
定理1 假設(H)成立,若(a1,a2)?∑p,則J滿足PS-條件。
定理1很好地描述了在f滿足一個較弱的條件下,J仍具有緊性條件。此結論對于方程(1)解的存在性有著廣泛的應用。本文將利用定理1來獲得在f滿足下列經典條件時,方程(1)正解的存在性。
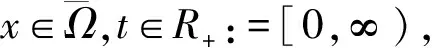
(H1) 存在l0,l∞<∞,使得
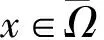
令
(4)
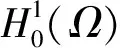
定理2 假設(H0)和(H1)成立,若l0>λ1且l∞<μ1,或l0<λ1且l∞>μ1,則方程(1)有一個正解。
在文獻[4]中,在l∞<μ1的假設下,作者利用拓撲度理論得到了方程(1)非負解的存在性,但是他們沒有討論l0>λ1且l∞<μ1這種情況下方程(1)正解的存在性。本文根據定理1,給出在l0>λ1且l∞<μ1這種情況下方程(1)正解的存在性的一個證明。文獻[12]證明了當l0<λ1且l∞>μ1時方程(1)有一個正解。本文利用定理1也可得到上述結論,并且證明過程與方法更加簡便。
2 定理1的證明
本節主要證明定理1.首先證明下面的引理1和引理2.
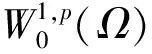
證明由于其證明過程類似于文獻[12]中的引理5,我們只對它進行一個簡單的敘述。
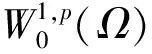
|f(x,t)|≤c1(1+|t|p-1),(x,t)∈Ω×R.
根據H?lder不等式和Sobolev嵌入定理可得:
(5)
類似地,有
(6)
眾所周知,
故由(5)和(6)得:
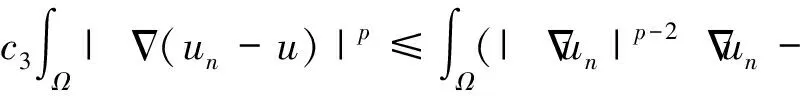
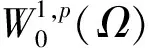
(7)
以下結論可參考文獻[13].為了讀者方便,在此給出其證明。
引理2 假設(a1,a2)?∑p,則存在C>0,使得
(8)
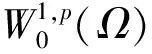
(9)
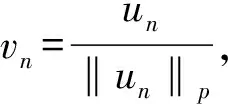
(10)
在(10)中對所有n取w=vn-v0,則有
從而有
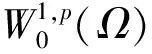
又(a1,a2)?∑p,從而v0=0.這與‖v0‖p=1矛盾。
下面,利用引理1和引理2,我們給出定理1的證明。
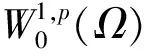
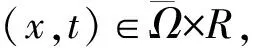
由(H)知,對任意的ε>0充分小,存在常數Cε>0,使得
|g(x,t)|≤ε|t|p-1+Cε,(x,t)∈Ω×R.
(11)
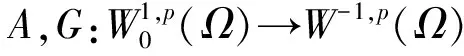
由引理2,J'(un)→0及式(11)知,對所有n有
(12)
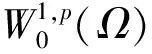
3 定理2的證明
本節利用定理1,分兩部分來證明定理2,即下列引理3和引理4.
引理3 假設(H0)和(H1)成立,若l0>λ1且l∞<μ1,則方程(1)有一個正解。
證明由(H0)、(H1)及l∞<μ1知,對ε∈(0,μ1-l∞),存在Cε>0,使得
f(x,t)≤(μ1-ε)tp-1+Cε,(x,t)∈Ω×R+.
(13)
則由(3)和(13)得:
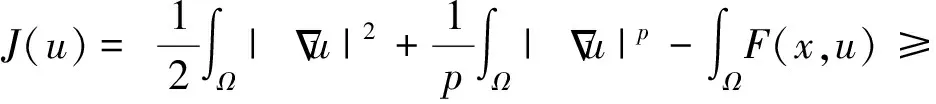
因此J下有界。
另一方面,由(H0)及l0>λ1可知,對ε∈(0,l0-λ1),存在δ>0,使得
(14)
取定φ1≥0且‖φ1‖2=1是λ1所對應的特征函數。則對s>0充分小,由(14)可得
從而J有負的下確界。
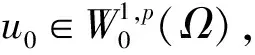
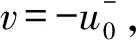
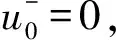
引理4 假設(H0)和(H1)成立,若l0<λ1且l∞>μ1,則方程(1)有一個正解。
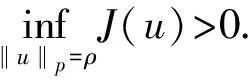
(15)
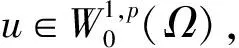
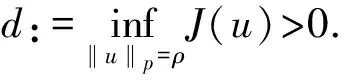
由(H0)、(H1)及l∞>μ1,存在ε∈(0,l∞-μ1)和Cε>0,使得
(16)
取定φ1≥0且‖φ1‖p=1為μ1所對應的特征函數,則由(3)和(16)得:
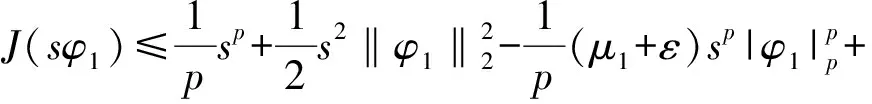
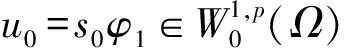
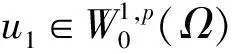
定理2的證明結合引理3和引理4即證。

