錨桿鉆機機械臂設計及動力學仿真分析

張 君，黃慶學，孟文俊，馬立峰

(1.太原科技大學 a.機械工程學院，b.太原重型機械裝備協同創新中心，太原 030024；2.中國煤炭科工集團太原研究院有限公司，太原 030006)

煤礦以井工開采為主，需要在井下開掘大量巷道。為了保證巷道暢通和圍巖穩定，迫切需要安全、高效和快速的巷道支護施工技術。煤礦巷道支護經歷了木支護、砌碹支護、型鋼支護到錨索聯合支護的漫長過程[1]。國內外的實踐經驗表明，錨桿支護是煤巷經濟、有效的支護技術。盡管目前錨桿支護已開始使用車載錨桿鉆機，鉆孔工藝已實現液控自動運行，但是拆、裝鉆桿，上錨桿和藥卷，鋪網等工序仍需人工手動作業，操作人員體力消耗較大；此外可呼吸性粉塵、鋪網時操作人員處于空頂區等危險因素嚴重威脅著他們的生命安全。為了提高錨護速度，改善操作人員安全性，減少其工作強度，就必須實現拆、裝鉆桿，上錨桿和藥卷，鋪網等工序動作的全自動化。機械臂代替人工的簡單且重復性工作已經是該行業的發展趨勢，同時機器人學的進步和應用是本世紀自動控制最有突出的成就，是當代工業領域最高意義的自動化[2-5]。文獻[6]指出在機器人結構設計中均基于pieper法則，各大機器人公司普遍采用關節坐標機器人來設計工業機器人。DAHLQUIP，KAUFMANN et al[7-8]對機器人手腕做了大量的研究，并且申請了相關專利。文獻[9]中指出在工業機器人機構學中，國內外學者大多數采用D-H坐標系來建立機器人的運動模型，通過結構設計參數來確定工業機器人各關節連桿的D-H參數，依據機器人的運動學方程來確定機器人的運動狀態。FENTON et al[10]用旋量法與矢量積法相結合來求解雅克比矩陣，該解法對自由度較高的機器人更加有效。PIPER et al[11]提出在實際運算中較為實用的方法——旋量法和微分法結合求解雅克比矩陣。文獻[12-13]表明在機器人動力學研究中，拉格朗日方程法可以通過系統系統能量的變化推導串聯型機械人的動力學方程，同時也可以通過計算機輔助編程，解決高自由度冗雜參數，輕松求解動力學方程。文獻[14-17]指出市面上動力學軟件都是基于拉格朗日方法建立模型的。MURPHY et al和JAIN et al建立了PUMA56的動力學模型，為后學研究提供參考。STAICU et al[18-19]，TSAI et al[20]應用虛工原理對Bendix手腕關節計算出了驅動力矩隨時間變化的曲線，提供了伺服電機的選型。CHEN[21]采用了拉格朗日方法建立了柔性機械臂的動力學模型。上述文獻都沒有提到井下錨桿鉆車機械臂的設計和動力學仿真分析的關鍵點和難點，參考資料較少，存在一定的空白點。為了滿足煤炭企業錨桿支護工作強度，提高支護操作安全性、減人增效等的需求，追蹤支護設備國際先進水平，非常有必要開展錨桿鉆機機械臂的設計工作和動力學仿真工作。為實現錨桿鉆車的全自動化、智能化提供理論支撐和技術儲備。

根據錨桿鉆車機械臂的實際需求建立了三維立體模型，并且在機械臂滿足運動學理論的前提下，用拉格朗日方法推導出機械臂的動力學方程。為了考察錨桿鉆機機械臂在實際工作狀況下是否能滿足受力需要，是否對整機的穩定性有一定的影響，故將機械臂的三維虛擬樣機模型導入多體動力學軟件ADAMS中進行不同工況下進行動力學仿真，去驗證在4個極限姿態下，機器臂的受力情況均能滿足實際需求。最后選取最惡劣的工況，運用仿真軟件Ansys Work Bench對伸縮臂承受的扭轉力較大處進行靜強度校核，以保證機械臂的強度要求。

1 機器臂設計

機械臂三維模型均在Solidworks2010中建立，整個機構的構成如圖1所示。該機械臂由底座、升降油缸、回轉桿、升降油缸II、伸縮臂套筒、回轉馬達及減速器等構成，每個執行機構都可以單獨安裝并且完成相應的測試實驗。該機械臂的姿態變化是靠兩個不同的油缸伸縮動作來實現的，包括兩臂的各自長度和相對角度的變化，錨桿臂端能實現準確空間位姿定位和點對點的高效工作。升降油缸安裝在回轉桿和底座之間，升降油缸的伸縮實現了回轉桿之間角度的變化。升降油缸II安裝在伸縮套筒和回轉桿之間，升降油缸II的伸縮實現了伸縮臂套筒與回轉桿之間相對角度的變化。伸縮臂套筒主要由內套筒和外套筒兩部分組成。自動臂架和伸縮臂套筒之間設有回轉馬達和減速器，用來實現伸縮臂套筒與回轉馬達和減速器的相對角度的變化。

圖1 機械臂三維模型Fig.1 3d mechanical arm model

2 機械臂動力學方程推導

在推導機械臂動力學方程前，根據圖1做適當的簡化，即回轉桿為連桿1，伸縮臂套筒為連桿2.回轉桿與底座之間的角度為θ1，回轉桿與伸縮臂套筒之間的角度為θ2.如圖2所示，連桿d1和d2的轉角分別為θ1和θ2，關節2和3的相應力矩分別是M1和M2，連桿d1和d2的質量分別是m1和m2.依據拉格朗日方程建立機械手動力學方程，推導如下：

E=EK-EP.

(1)

(2)

圖2 機械臂數學簡化模型Fig.2 Mechanical arm simplified mathematical model

連桿1的動能和勢能為：

(3)

EP1=-m1gd1cosθ1.

(4)

連桿2的動能和勢能為：

(5)

EP2=-m2gd1cosθ1-m2gd2-cos(θ1+θ2) .

(6)

兩個連桿的總動能和總勢能分別為：

(7)

EP=EP1+EP2=-(m1+m2)gd1cosθ1-m2gd2cos(θ1+θ2) .

(8)

將兩個連桿的總動能和總勢能的表達式式(7)-式(8)代入拉格朗日推導式中得：

(9)

對E求偏導數和導數：

(10)

(11)

(12)

(13)

(14)

(15)

將相應各導數和偏導數都代入拉格朗日方程動力學方程中得：

(16)

(17)

3 機械臂動力學仿真

機器臂動力學方程推導是虛擬樣機仿真實驗的前提和基礎。目前多剛體建模方法主要有2種，即矢量力學分析法和分析力學方法[22-23]。分析力學方法以拉格朗日方程為主，該方法采用廣義坐標系。ADAMS全名為機械系統動力學自動分析，該軟件是美國機械動力公司開發的虛擬樣機分析軟件，其建模過程基于拉格朗日方法[24-31]。ADAMS從20世紀90年代進入中國以來，廣泛應用于機械制造、航空航天、鐵道、兵器、石油化工、汽車交通等領域。運用虛擬樣機技術，可以大大簡化機械產品的設計開發過程，大幅度縮短產品開發時間和降低產品費用，能夠提高產品的系統性能，獲得最優化的設計產品。機械臂模型中的各個零件特性參數是根據物理樣機實際設計需要設置的，對各關節施加相應的運動約束副，并觀察各連桿在運動極限狀態下的力矩變化，檢驗機械臂設計的合理性。文中考察鉆架在恒定外負載作用下，通過調整2個油缸之間的行程看是否能實現鉆架在整個工作空間的所有工作位置，找到整機在不同姿態下打錨桿時的受力最惡劣工況，查看該工況下油缸受力變化及伸縮臂受力狀況。

3.1 數字化模型建立

將錨桿鉆車工作平臺上不影響主體強度的部分零部件(包括鉆架、銷軸、擋銷板、內套筒壓板等)進行適當簡化，壓縮焊縫倒角和螺紋小孔(見圖3).運用Solidworks三維軟件對零部件進行虛擬裝配和全局干涉檢查，可以有效降低各零部件間的相互干涉和配合錯誤率，同時對零件賦予質量屬性，避免了在ADAMS中進行模型修改等繁瑣操作，確定各零部件裝配無干涉后導入到ADAMS環境下，進行參數設置和約束條件施加。具體操作為在底座與大地之間施加固定副；底座與回轉桿之間施加球副；鉆架升降油缸和鉆架升降油缸II的缸筒之間施加球副；回轉桿與鉆架升降油缸活塞桿之間施加球副；回轉桿與伸縮臂外套筒之間施加球副；2個油缸缸筒與缸桿之間均施加平移副。在臂架上施加重力載荷；內套筒減速器安裝板上施加遠程力，作用點在鉆箱中心，方向垂直向下，大小為3.5×104N.仿真時間4 s，仿真步長0.001.具體仿真參數設置如表1所示。

圖3 輸入模型Fig.3 Input model

3.2 仿真結果分析

仿真時間1 s時，鉆架升降油缸完全伸出，鉆架升降油缸II完全收縮，此時模型姿態見圖4.從0～1 s的仿真過程中可以觀察出升降油缸在逐漸伸出過程中，整體模型的受力變化。

表1 仿真設置Table 1 Simulation settings

圖4 仿真時刻1 s時模型姿態及受力情況Fig.4 Simulation time 1s model attitude and force situation

仿真時間2 s時，鉆架升降油缸完全伸出，鉆架升降油缸II也完全伸出，此時模型姿態如圖5所示。從1～2 s的仿真過程中可以觀察出當鉆架升降油缸保持最長、鉆架升降油缸II逐漸伸出的過程中，整體模型的受力變化。仿真時刻3 s時，鉆架升降油缸完全收縮，鉆架升降油缸II仍完全伸出，此時模型姿態如圖6所示。從2～3 s的仿真過程中可以觀察出當鉆架升降油缸II保持最長，同時鉆架伸縮油缸逐漸收縮過程中，整體模型的受力變化。

圖5 仿真時刻2 s時模型姿態及受力情況Fig.5 Simulation time 2 s model and stress distribution

仿真時間4 s時，鉆架升降油缸完全收縮，鉆架升降油缸II也完全收縮，此時模型姿態見圖7.從3～4 s的仿真過程中可以觀察出當鉆架升降油缸保持最短、鉆架升降油缸II逐漸收縮的過程中，整體模型的受力變化。

由圖8仿真結果表明，鉆架升降油缸在3 s時受力最大，峰值達到20.8×104N.鉆架升降油缸II在初始時刻受力最大，峰值達到18.4×104N.

圖6 仿真時刻3 s時模型姿態及受力情況Fig.6 Simulation time of 3 s model attitude and force situation

圖7 仿真時刻2 s時模型姿態及受力情況Fig.7 Model attitude and force situation of 2 s at simulation time

圖8 仿真過程中鉆架升降油缸和鉆架升降油缸II受力變化情況Fig.8 In the process of simulation drill rack lifting oil cylinder and drill lifting oil cylinder II stress changes

由圖9仿真結果表明，伸縮臂外套筒在3 s時受彎矩最大，峰值達到2.19×107N·mm.伸縮臂受力最大時刻為初始時刻，峰值達到1.67×105N·mm.機械臂油缸受力變化仿真結果如表2所示。

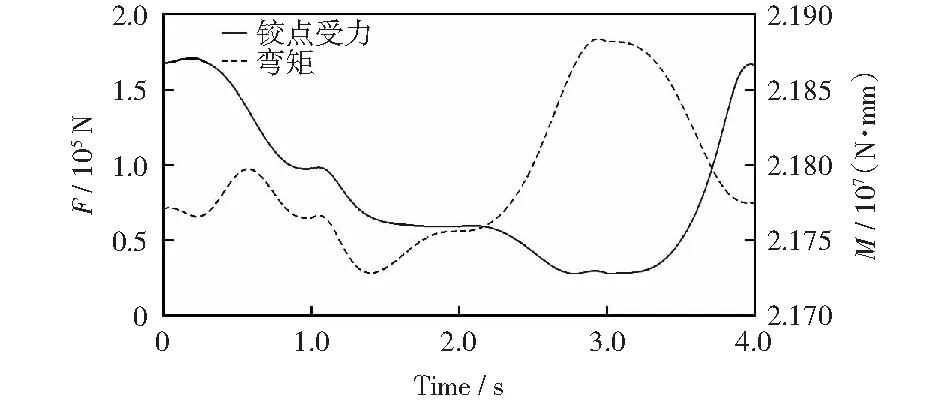
圖9 仿真過程中伸縮臂外套筒下端鉸點的受力和彎矩圖Fig.9 In the simulation process, the force and bending moment of the lower end of the sleeve of the telescopic arm are shown

3.3 伸縮套筒強度分析

由于在仿真時刻3 s時，升降油缸受力超過該油缸的許用極限抗壓力1.9×105N，故需進一步考察作用3.5×104N外力下產生的扭矩對伸縮套筒強度的影響。將三維模型導入Ansys Work Bench環境中進行仿真。輸入模型及描述，將伸縮臂上不影響主體強度的部分零部件進行適當簡化，壓縮焊縫倒角和螺紋小孔。設置材料屬性參數，彈性模量為2×105MPa，泊松比為0.3；采用國際標準單位制單位；網格劃分單元類型為Solid；采用以六面體為主的網格單元，網格大小為0.010 m；內套筒筒體和與內套筒接觸的壓塊網格局部細化，細化大小為0.005 mm.將外套筒后端鉸點及下側油缸鉸點固定作為支撐工況的邊界條件；在減速器安裝面施加遠程力及鉆架自重力，遠程力作用點位于鉆架鉆箱中心處，大小為3.5×104N，用來模擬鉆架打鉆力。內套筒與8個壓塊之間施加摩擦系數0.2.仿真計算結果表明，支撐工況下的伸縮臂套筒最大應力為619.5 MPa，最大值出現負載一側的豎直壓塊上，應力云圖如圖10所示。

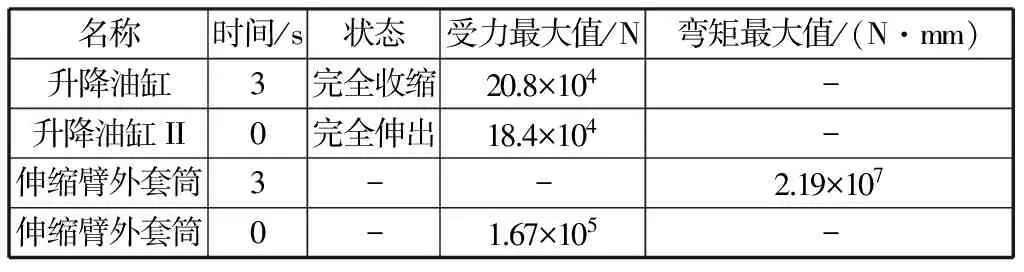
表2 機械臂油缸受力變化仿真結果Table 2 Mechanical arm dynamics simulation results

圖10 伸縮臂套筒應力Fig.10 Telescopic arm sleeve stress

由圖11可知，伸縮臂套筒的最大變形為4.1 mm，最大值出現在內套筒上位于負載一側的減速器安裝面上。

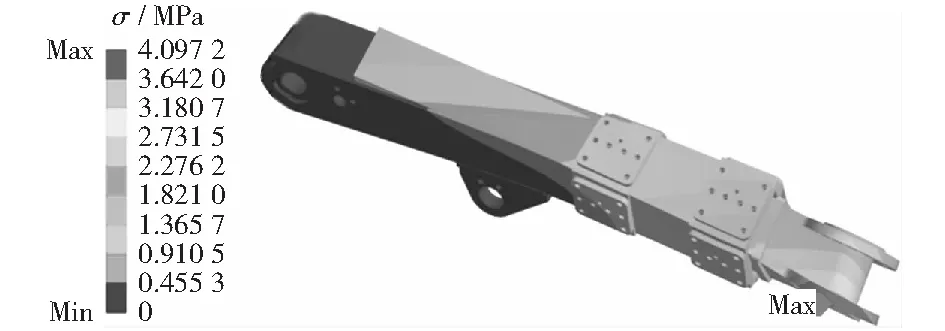
圖11 伸縮臂套筒變形Fig.11 Deformation of telescopic boom sleeve

由圖12可知，外套筒受力最大為445.5 MPa，位置在下側油缸耳座根部焊縫交叉點處。該處存在一定的應力集中。

圖12 外套筒受力Fig.12 Outer sleeve force

由圖13可知，內套筒受力最大為410 MPa，位置為內部油缸耳孔外沿處。該極值為一個尖點，存在應力集中。拋開尖點，其他部位最大應力為315.9 MPa.

圖13 內套筒受力Fig.13 Inner sleeve force

由圖14可知，8塊內套筒壓板受力不均勻，最大受力為靠近負載一側的豎壓板，極值為619.5 MPa，位置為與內套筒接觸的邊線上一點。該極值為一個點，存在應力集中。拋開該點，其他部位最大應力為390 MPa.由計算結果分析可知，當伸縮臂在3.5×104N外力作用下扭轉時，受力較大的零部件為內套筒壓塊和內套筒。伸縮套筒受扭靜強度仿真結果如表3所示。由于伸縮臂在動力學仿真3 s時承受的扭轉力較大，通過對其進行扭轉靜強度校核，仿真結果表明伸縮套筒受扭靜強度滿足設計要求。

圖14 內套筒壓板受力Fig.14 Inner sleeve pressure plate

表3 伸縮套筒受扭靜強度仿真結果Table 3 Simulation results of torsional static strength of telescopic sleeve

4 結論

1) 針對錨桿鉆機機械臂設計及機械臂油缸動力學分析問題展開了研究。基于機器臂設計運動學理論，推導出錨索鉆機機械臂動力學方程。

2) 完成了機器臂的虛擬樣機模型的建立和與多體動力學Adams軟件的無縫鏈接，進行了動力學仿真，觀察在4個極限姿態工況下機器臂油缸受力的情況。結果表明，在時刻3 s時，鉆架升降油缸完全收縮，鉆架升降油缸II仍完全伸出，此時鉆架升降油缸在3 s時受力最大，峰值達到2.08×105N.

3) 由于在仿真時刻3 s時，升降油缸受力超過該油缸的許用極限抗壓力1.9×105N，故需要運用Ansys Work Bench對伸縮臂承受扭轉力較大處進行扭轉靜強度校核，才能滿足機械臂動力學要求。