社區網的增長趨向及其分形特征分析

沈陽理工大學信息科學與工程學院 苑 勛 徐 野

東北大學軟件學院 黃利萍

復雜網絡是指具有自組織、自相似、吸引子、小世界、無標度中部分或全部性質的網絡。復雜網絡出現在各個學科領域，如生物學、物理學，甚至社會科學中。在過去的若干年中，許多關于復雜網絡的規律被發現，如服從雙向冪律分布的萬維網，具有無尺度的特點藝人網絡，呈現指數級衰減的送電網則。

本文通過研究一個社區網實例，確定社區網的分形規律，分析它的維數，做出奇異吸引子混沌軌道運動形式的數學模型，揭示其網絡的復雜性及其在生長變化中的分形或混沌特征，確定預測模型的數學形式。

1.幾個定義

定義1 社區網沈陽市某社區的全部業主，具有想建立聯系想法的業主之間相互連接，組成業主為節點、相互聯系為邊的網絡，稱為社區網。

定義2 新增節點，社區網中新注冊的用戶代表的節點稱為新增節點，一天內新增節點數用Nb表示。

定義3 增聯節點，社區網中已注冊用戶若增加至少一個連接稱為增聯節點，一天內的增聯節點數用Ns表示

定義4 眠聯節點，社區網中的已注冊用戶一天之內連接保持不變稱為眠聯節點，一天內的眠聯節點數用Nd表示。

定義5 覺聯節點，社區網中的眠聯結點如果一天之內至少增加一條邊則稱為覺聯節點，一天內的覺聯節點數用Na表示。

定義6 規模增速，設社區網中節點數為N，社區網規模增速r可用下式表示：

2.模型

2.1 讓模型體現社區網的震蕩性

由定義2～6及和 (1)，我們計算社區網的規模增速r，通過觀察計算得出的三周內節點增長速率圖可知：社區網規模增速在不斷地震蕩。從肉眼觀察可以看出震蕩曲線表現出一定的周期性特點。因為震蕩的曲線可以用不同周期的正弦余弦函數及其組合表示，所以可以將r轉換為(2)來表示。

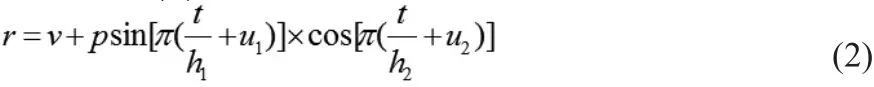
其中v為總體偏移量，p為振幅。h1、 h2為震蕩半周期，單位為天。u1、 u2為震蕩幅角。

把式(2)中r的表示代入Logistic模型，就是本文對Logistic模型的進一步修改，使其能夠表示周期性的變化。

2.2 求解r表示式的系數

下面采用浮點型遺傳算法求解r表示式的系數。

首先定義遺傳基因，一個基因中包含了所有r表示式中的待定參數如(3)所示：

(2) 生成最初的基因群體，即若干組r表示式中的待定參數。本文中基因群的基因數為N=100，每個基因的編碼值由隨機算法生成。

(3) 匹配度估計函數

由基因編碼確定的參數值計算出的r(t)應當與采樣值r*(t)越接近越好。我們用社區網25天的采樣數據來計算r(t)與r*(t)的差，由此得到匹配度估計函數。

利用匹配度估計函數計算每個基因編碼（即每組參數取值）的分數，該分數為匹配度估計函數的倒數，即：

(4) 挑選優秀基因

設有隨機數m(0＜m＜1)，挑選分數比m高的前w個基因作為進一步繁殖的種群。為簡化計算，復制選出的w個個體，刪除按分數排序的后w個個體，保持種群個體數不變，進行下一步的繁殖。

(5) 雜交

繁殖種群個體數設為N，設MP=(x1…xi…xj…xn) 為雜交池中，用隨機方法從中選擇xi、xj兩個基因進行雜交[10]，基因中每個參數的雜交方式類同，如在參數v上進行雜交，公式為

按照上述雜交操作，對每個基因中的每個參數進行修正。修正的同時要防止參數衰減到0，當其值小于0.01時，設置為0.01。

(6) 變異

對雜交的到的N個基因中的每個參數進行變異，變異概率為0.3。參數v 的變異算法公式如下：

(7) 結束判斷

本文采用雙重結束判斷算法，一個結束判斷條件是(為結束時達到的分數下限，在本文中采用0.1作為下限)；另一個結束判斷條件是遺傳算法的循環次數，如果循環次數達到上限，結束計算，不管此時score是否越過下限s。本文中設定的循環次數上限為1000，實驗表明循環次數達到這一數值可以保證產生優良的后代。

2.3 擬合結果與評價

2.3.1 收斂分析

經過1000次遺傳算法的循環，得到的最優基因（參數組），代入社區增長模型的結果如式(8)：

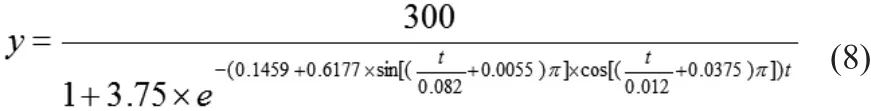
由此可以從圖上看到100次循環以后，遺傳基因達到最優，其后900次循環中，基因的分數變化不大，所以可以認為該遺傳算法收斂，得到的結果較好。

2.3.2 擬合精確度分析

本文定義相對擬合誤差ε，據此分析模型的擬合程度。定義7 設社區網規模采樣數據原始值為y*(ti)，用擬合模型計算出的值為y(ti)(i31，i?N)，則相對擬合誤差ε定義為誤差和的均值占原始數據均值的比重，公式如下：

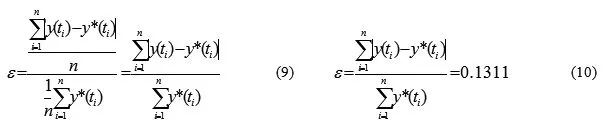
其中，i， n(n=25)表示采樣天數為25天，每天采集一個數據。采用平均誤差占平均原始值的比重表示相對的誤差程度。

由式(9)，可以計算出25天內社區網規模的相對擬合誤差，故社區網規模增長模型的擬合精確度為1-0.1311=86.89%，結果較好，可以接受。

3.社區網規模增長的混沌分析

3.1 社區網規模增長曲線

由前面所述的社區規模增長的數學模型可以做出如圖1的增長曲線。

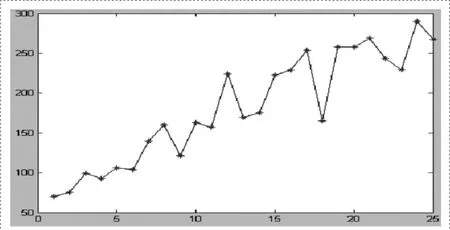
圖1 增長趨向圖（x軸-增長時間/天，y軸-網絡節點值）

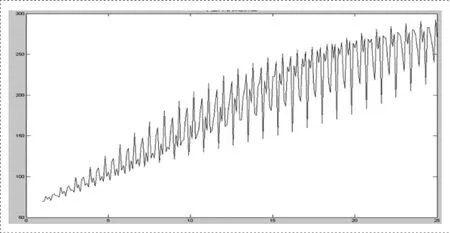
圖2 增長趨向圖（x軸-增長時間/0.1天，y軸-網絡節點值）

從圖1可以看出，社區網規模震蕩向上走高，曲線呈現鋸齒狀，不光滑。為了表明曲線的特點，便于觀察，我們將圖中時間單位由1天變為0.1天，再次繪圖得到如圖2的曲線。

我們得到圖2的曲線顯示社區網規模曲線是一條連續向上增長的波動曲線，曲線仍然呈現鋸齒狀，在每個取值點都不可導，表現出混沌分形的特點。下文我們計算這一曲線的維數。

3.2 維數的計算方法

計算社區網規模增長的維數，首先取得采樣時間序列，將一維的數據轉換成m維數據，m依次取值為2，4，8，10，15，18等等。然后根據表2的計算方法，對每個m值計算相應的D2值，D2就是m的關聯維數。如果隨著m的增大，D2收斂于某一飽和值，說明社區網規模增長系統具有混沌分形的特點。反之如果D2不隨m增大而收斂，而是趨向于無窮，則系統不具有混沌性。表2說明了與m相關聯的維數D2的計算方法。

表2 計算時間序列的關聯維數算法

3.3 社區網規模增長系統的維數

采用表2的算法，對m=2,4,8,10,12,15,18,20 計算r和cr，繪出ln(r)-ln(cr)曲線，從圖中可以看出，m=12,15,18,20時曲線的直線部分具有平行性，它們的斜率基本相同，其斜率就是D2（關聯維數），該值收斂。計算可得：

由以上計算可知社區網規模增長系統具有混沌分形特性，其關聯維數是在2和3之間的分數維。

3.4 社區網規模增長系統的長期預測

根據文獻，維數為D2的分形混沌系統，設D2向上取整的值為D，則至少需要D個方程描述系統中D個重要的物理規律，才能實現長期較準確的預測。

由式(12)，社區網規模增長系統的關聯維數為2、3之間的分數維，為了對該系統進行長期預測，至少需要3個方程為其系統建模，公式如下：

式中x,y,z為表達社區網系統重要物理規律的物理量，x(n)為x的n階導數，y(n)為y的n階導數，z(n)為z的n階導數，n=1，2，3…。

式(13)表達了社區網混沌系統內在的運動規律，由于本文中采樣數據較少，不能夠確定f1～f3中的具體參數，因而將這部分計算作為我們下一步的工作。

4.小結與展望

因為Logistic模型有效反映了有限資源條件下生物種群增長的規律，和社區網絡具有內在相似性，本文采用Logistic模型為社區網落規模增長趨像建立了數學模型。因為社區網規模在震蕩中增長，本文增加了模型中的三角函數因子，改進了原模型，是其能夠反映震蕩特性，模型參數用遺傳算法進行搜索，得到較為優異的擬合值。

模型曲線連續但不可微，呈現鋸齒狀，表現出混沌分形特性，本文利用維數計算方法計算得到了社區網規模增長系統的維數為2.062。維數計算收斂，表明社區網規模增長系統中混沌分形性是真實存在的。

最后本文指出要對社區網規模增長系統進行長期較為準確的預測，必須至少采用三個以上的物理量及其多階導數的三個以上的方程式描述內在的重要物理規律。本文給出了上述數學模型，我們下一步的工作便是求解模型中的參數。