彈流潤滑條件下的深溝球軸承徑向剛度及油膜厚度分析

楊杰，買買提明·艾尼,2，王曉亮，武園園，王國建

(1.新疆大學 機械工程學院，烏魯木齊 830049;2.西安交通大學 結構強度和振動國家重點實驗室，西安 710049)

深溝球軸承摩擦因數小、極限轉速高，且非常耐用，無需經常維護，常應用于精密儀表、變速箱、電動機中，是該類機械的重要傳動部件。深溝球軸承徑向剛度直接影響著轉子的動力學特性，故有必要對其徑向剛度進行研究。文獻[1-8]均有關于軸承的徑向剛度的計算,但計算均基于Hertz接觸理論，軸承處于干摩擦狀態，未考慮油膜潤滑的影響。文獻[9]通過試驗證明了潤滑油膜會影響深溝球軸承的剛度；文獻[10]基于流固耦合法對滾動軸承的剛度進行分析；文獻[11]闡述了彈流潤滑會對滾動軸承接觸剛度產生影響。鑒于此，考慮油膜潤滑的影響建立深溝球軸承綜合徑向剛度數學模型，并基于C++編寫計算軸承徑向剛度的程序,分析軸承載荷、轉速以及潤滑油黏度對軸承徑向剛度的影響。

1 深溝球軸承徑向剛度數學建模

在潤滑油充盈時,深溝球軸承的鋼球被油膜抬起，外圈剛度由鋼球與外圈溝道的Hertz接觸剛度和油膜剛度串聯組成，內圈剛度由鋼球與內圈溝道的Hertz接觸剛度和油膜剛度串聯組成。滾動軸承的綜合剛度由內、外圈剛度串聯而成[12]。

1.1 Hertz接觸剛度

滾動軸承的接觸剛度指軸承內外圈產生單位位移所需的外載荷，僅受純徑向載荷且無徑向游隙的深溝球軸承，如圖1所示，在“偶壓”狀態下，鋼球最大載荷Qmax與徑向載荷Fr之間的關系為[13]40-42

圖1 深溝球軸承的徑向載荷示意圖Fig.1 Diagram of radial load of deep groove ball bearing

(1)

式中：Z為鋼球數量；φj為鋼球的方位角。

在純徑向載荷作用下，深溝球軸承僅在徑向方向產生位移，其徑向位移可用最大接觸載荷處套圈法向彈性變形表示，即

(2)

γ=Dw/Dpw，

式中：ν1，ν2分別為鋼球與套圈材料的泊松比；E1，E2分別為鋼球與套圈材料的彈性模量；F(e)，E(e)分別為第一類和第二類完全橢圓積分函數；e為橢圓參數；Qmax為套圈最大接觸載荷。對于內圈，±取+，對于外圈，±取-；Dw為鋼球直徑；Dpw為球組節圓直徑；f為套圈溝曲率半徑系數。

根據文獻[13]10-13可知橢圓參數為

e=(1-1/k2)1/2，

(3)

k=1.033 9(Ry/Rx)0.636 0，

對于內圈，±取+，對于外圈，±取-。第一類和第二類完全橢圓積分函數為

F(e)=1.527 7+0.601 3ln(Ry/Rx)，

(4)

E(e)=1.003+0.596 8(Rx/Ry)。

通過(1)～(4)式可得

(5)

由(5)式可得鋼球與套圈溝道的Hertz接觸剛度為

(6)

1.2 彈流潤滑油膜剛度

大多數滾動軸承工作在潤滑狀態，深溝球軸承工作時鋼球與溝道之間會充滿潤滑油，接觸區域會處于彈流潤滑狀態(EHL),且彈流引起的油膜剛度會對軸承的剛度產生重要影響。

Hamrock-Dowson采用數值計算法得出等溫橢圓接觸的點接觸中心油膜厚度[14]，將中心油膜厚度量綱一化為

(7)

G=αE′，

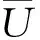
圖2 鋼球與內外圈接觸表面速度Fig.2 Surface speed of contact between steel ball,inner and outer rings

假設深溝球軸承外圈固定，內圈旋轉，鋼球與內圈溝道的接觸點在x，y方向的速度分別為ui，vi，鋼球與外圈溝道的接觸點在x，y方向的速度分別為ue，ve。

外圈固定，則外圈轉速ne為0。鋼球公轉速度為

(8)

式中：ni為內圈轉速。

由于鋼球的自轉，鋼球與內、外圈溝道接觸點的速度相同，即

(9)

則鋼球與內、外圈溝道接觸點的平均速度為

(10)

由(7)，(10)式可得中心油膜厚度為

(11)

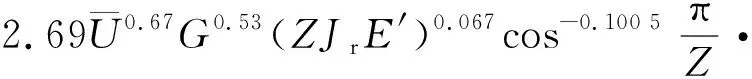
鋼球與套圈溝道接觸的油膜剛度為

(12)

1.3 深溝球軸承綜合徑向剛度

軸承內、外圈剛度分別為

(13)

軸承剛度由內、外圈剛度串聯得到

(14)

2 計算流程

軸承綜合徑向剛度受轉速、潤滑油黏度及載荷的影響。基于C++編寫計算軸承徑向剛度的程序，流程圖如圖3所示。主要步驟如下：

圖3 軸承綜合徑向剛度計算流程圖Fig.3 Flow chart for calculation of synthetical radial stiffness of bearing

1)輸入軸承結構、材料和潤滑油參數；

2)分別計算鋼球與內、外圈接觸的Hertz接觸剛度和油膜剛度；

3)內、外圈徑向剛度由鋼球與套圈溝道接觸的Hertz接觸剛度和油膜剛度串聯而成,計算內、外圈徑向剛度；

4)軸承綜合剛度由內、外圈剛度串聯而成,計算軸承綜合徑向剛度。

3 實例分析

以深溝球軸承6003為例分析，其主要結構參數見表1。潤滑油黏度為0.02 Pa·s，黏壓系數為2.3×10-8Pa-1。內外圈和鋼球材料均為GCr15，其材料參數為：彈性模量為207 GPa，泊松比為0.3。

表1 主要結構參數Tab.1 The main structural parameters

3.1 徑向載荷對軸承綜合徑向剛度和油膜厚度的影響

在分析深溝球軸承時，忽略轉動過程中溫度對軸承剛度的影響。在轉速為5 000 r/min-1，潤滑油黏度為η=0.02 Pa·s，黏壓系數α=2.3×10-8Pa-1時深溝球軸承的綜合徑向剛度和中心油膜厚度隨徑向載荷的變化如圖4所示。由圖可以看出，隨徑向載荷增大軸承剛度增大。在載荷為0～1 700 N時，軸承的綜合徑向剛度和中心油膜厚度分別急劇增大和減小，當載荷超過1 700 N時，兩者均變化緩慢。

圖4 徑向載荷對軸承綜合徑向剛度和油膜厚度的影響Fig.4 Effect of radial load on synthetical radial stiffness and oil film thickness of bearing

在考慮油膜情況下，軸承的綜合徑向剛度略小于單純Hertz接觸剛度。為便于分析，定義接觸剛度與綜合徑向剛度之差為剛度差ΔK，其隨徑向載荷Fr的變化如圖5所示。由圖可以看出，載荷小于1 kN時，剛度差變化較大，油膜對軸承剛度影響較大；載荷大于1 kN時，油膜對軸承的剛度影響小。

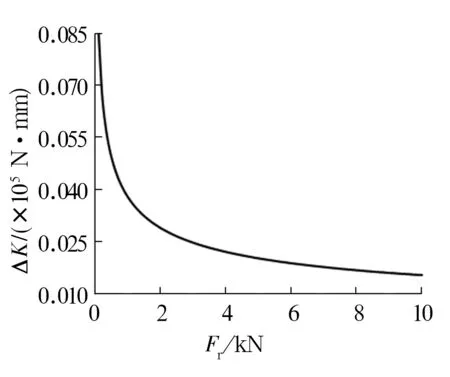
圖5 徑向載荷對軸承綜合徑向剛度差ΔK的影響Fig.5 Effect of radial load on synthetical radial stiffness difference of bearing ΔK

3.2 轉速和潤滑油黏度對軸承綜合徑向剛度和油膜厚度的影響

在徑向載荷Fr=1 kN的情況下，轉速和潤滑油黏度對深溝球軸承綜合徑向剛度和油膜厚度的影響如圖6所示。由圖可以看出，轉速接近0時，潤滑劑黏度對軸承的綜合徑向剛度和油膜厚度影響較小，隨轉速增大，軸承的綜合徑向剛度和油膜厚度分別呈減小和增大趨勢。轉速越大對二者的影響越大；相同轉速下隨潤滑油黏度增大，軸承的綜合徑向剛度減小，而油膜厚度增大。

圖6 轉速和潤滑油黏度對軸承綜合剛度和油膜厚度的影響Fig.6 Effect of rotational speed and viscosity of lubricating oil on synthetical stiffness and oil film thickness of bearing

4 結束語

考慮油膜潤滑的影響建立了深溝球軸承綜合徑向剛度數學計算模型，分析了徑向載荷、轉速、潤滑油黏度對軸承綜合徑向剛度的影響。結果表明：徑向載荷、轉速、潤滑油黏度均會對軸承徑向剛度產生重要影響，在分析軸承運動學特性時應考慮潤滑油的作用，而不應只考慮干摩擦的狀態。分析結果可為該類軸承的設計提供參考。