徑向磁力軸承多因素耦合研究
樓英邦,張小玉,方璽,呂泳,吳華春
(1.武漢理工大學a.理學院 工程結構與力學系,b.機電工程學院,武漢 430070;2.新材料力學理論與應用湖北重點實驗室,武漢 430070)
純電磁磁力軸承是利用電磁力將轉子穩定地懸浮于空中的軸承,由于定子和轉子間不接觸,因此具有無摩擦、高精度、無需潤滑、高轉速等優點,具有廣闊的研究前景[1-2]。然而,傳感器在安裝和測量的過程中存在誤差,且轉子轉速升高時,特別在高速下,轉子繞慣性中心旋轉,由于其材料分布不均勻,機械加工、裝配精度低等原因,造成轉子的幾何中心與慣性中心不重合,從而產生偏心。如果忽略偏心產生的耦合力的影響,就無法發揮磁懸浮轉子高速高精的優越性。耦合力的存在影響了控制系統性能,導致轉子失穩。特別是在磁懸浮硬盤驅動器、微型磁懸浮陀螺等微小磁懸浮轉子應用領域,耦合力的影響不能忽略。
為減輕或消除磁力軸承轉子系統中存在的力耦合和力矩耦合,針對八極徑向磁力軸承,以轉子偏心距為變量,文獻[3]分析計算了電磁力的分布,推導了徑向磁力軸承沿周向任意點處電磁力的表達式。文獻[4]表明由于忽略漏磁及定子鐵心和轉子的磁阻等原因,使得理論分析存在較大誤差,從而采用有限元對磁力軸承進行模擬分析,證明了ANSYS分析的可靠性。文獻[5]表明在正交偏心的情況下,考慮單因素偏心距對耦合力的影響,運用有限元軟件ANSYS對磁力軸承進行耦合數值計算與分析。文獻[6]表明為了研究振動特性,在磁懸浮高速電動機轉子軸承系統的臨界轉速下,把轉子-軸承系統簡化模型導入ANSYS Workbench中,對振動情況進行了仿真分析。文獻[7]建立了耦合剛度模型,表明徑向和軸向之間的弱耦合性有利于設計CRAMB系統的控制器和動態穩定性控制。
目前,關于多因素對耦合力影響的研究不足,因此,通過研究偏心距、工作電流對耦合力的影響,運用理論計算和有限元軟件分析耦合力的變化規律,并定量分析耦合力在偏心距和工作電流影響下,理論值較仿真值的相對誤差及通道間的耦合程度,以期為理論公式的適用范圍提供參考。
1 徑向磁力軸承的力耦合
一般情況下,當轉子旋轉時定子和轉子存在偏心,如圖1所示。由于徑向磁力軸承的對稱性,圖中只顯示出一組磁極的情況。其中:e為偏心距;α為偏心角;b為磁極寬度;R為定子內半徑;r為轉子外半徑;Δs為定子磁極上的微小寬度;fi為Δs對應的電磁力。
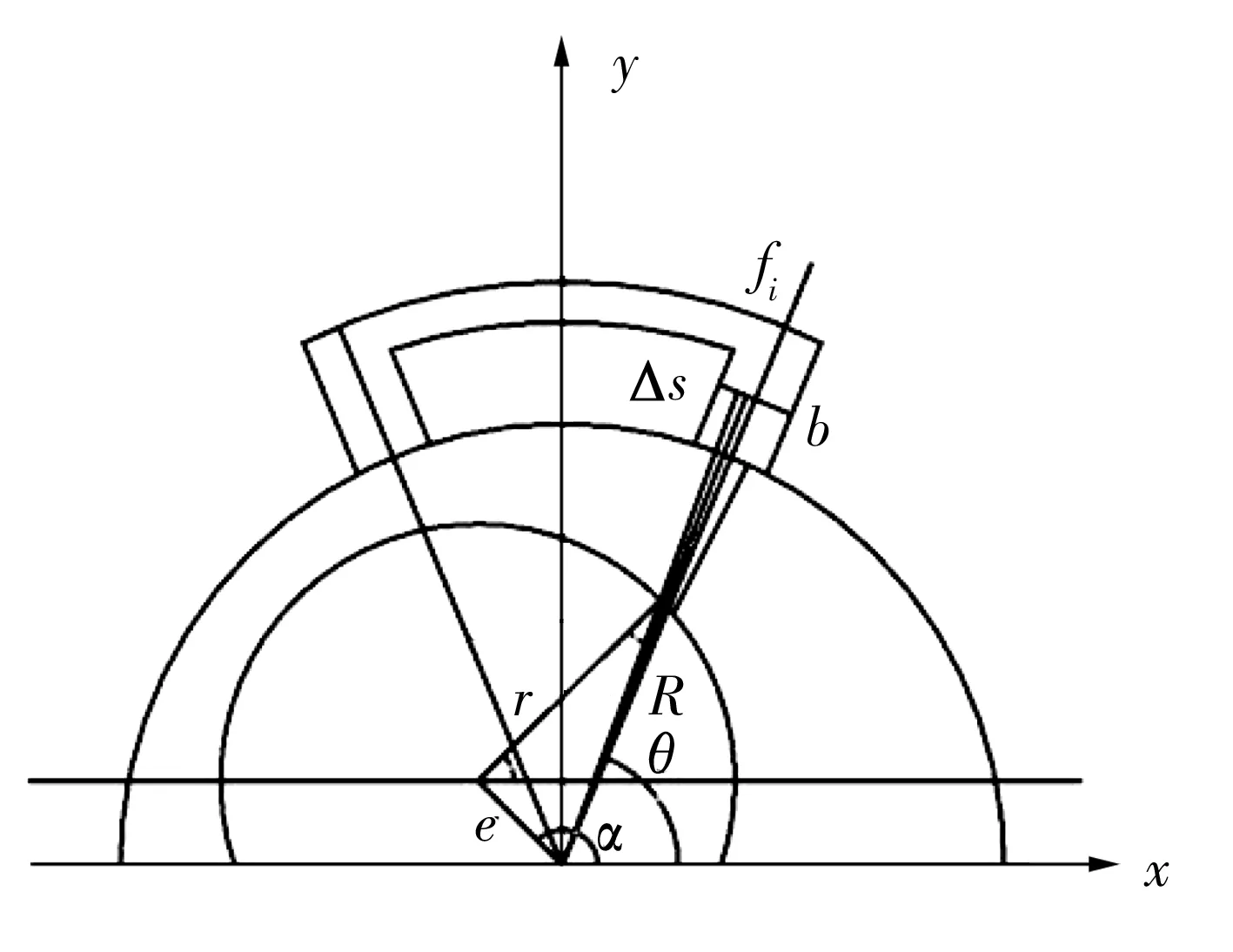
圖1 轉子和定子在偏心下的幾何關系Fig.1 Geometrical relationship between rotor and stator under eccentricity
由磁力軸承的工作原理可推導出懸浮力為[8]43
(1)
式中:I0為工作電流;μ0為空氣磁導率;L為軸承厚度;n為線圈匝數;N為磁極序號,以直角坐標逆時針方向排列,如圖2所示。
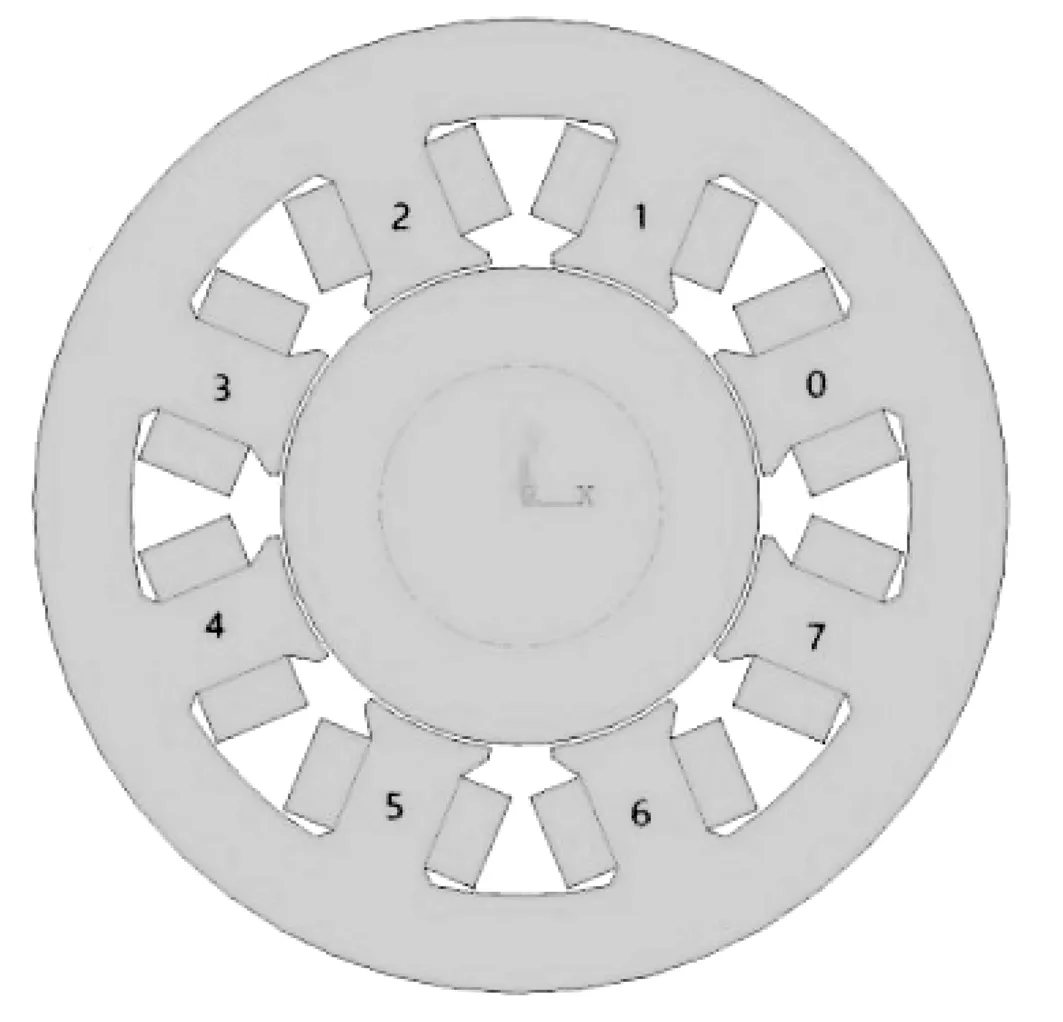
圖2 磁極序號示意圖Fig.2 Diagram of pole number
為了便于分析耦合力的大小和影響,將x軸和y軸上的2組磁極的電磁力分開計算,并將總懸浮力F向x和y軸投影,則
N=0,3,4,7時
(2)
N=1,2,5,6時
(3)
式中:F的第1個下標表示磁極的布置方向,第2個下標表示電磁力的投影方向,如Fxy表示x方向的磁極產生的電磁力在y軸的分力。
2 ANSYS計算模型
磁力軸承參數如下:n=80匝,定子外徑100 mm,R=25 mm,r=24.5 mm,單邊氣隙為0.5 mm,L=30 mm,b=10 mm。根據磁力軸承的對稱結構,簡化成二維模型進行計算。
建立平面模型,選用二維8節點單元PLANE53,只選用磁矢勢Az這一個自由度。磁力軸承相應部分的相對磁導率見表1。定子和轉子外層是鐵磁材料,其磁化B-H曲線如圖3所示;轉子內層由45#鋼制成。由于只研究磁力軸承內部的磁場分布,故以有限元模型中的最外圍所有節點作為邊界,令Az=0。磁力軸承有限元模型如圖4所示。

表1 相對磁導率Tab.1 Relative permeability
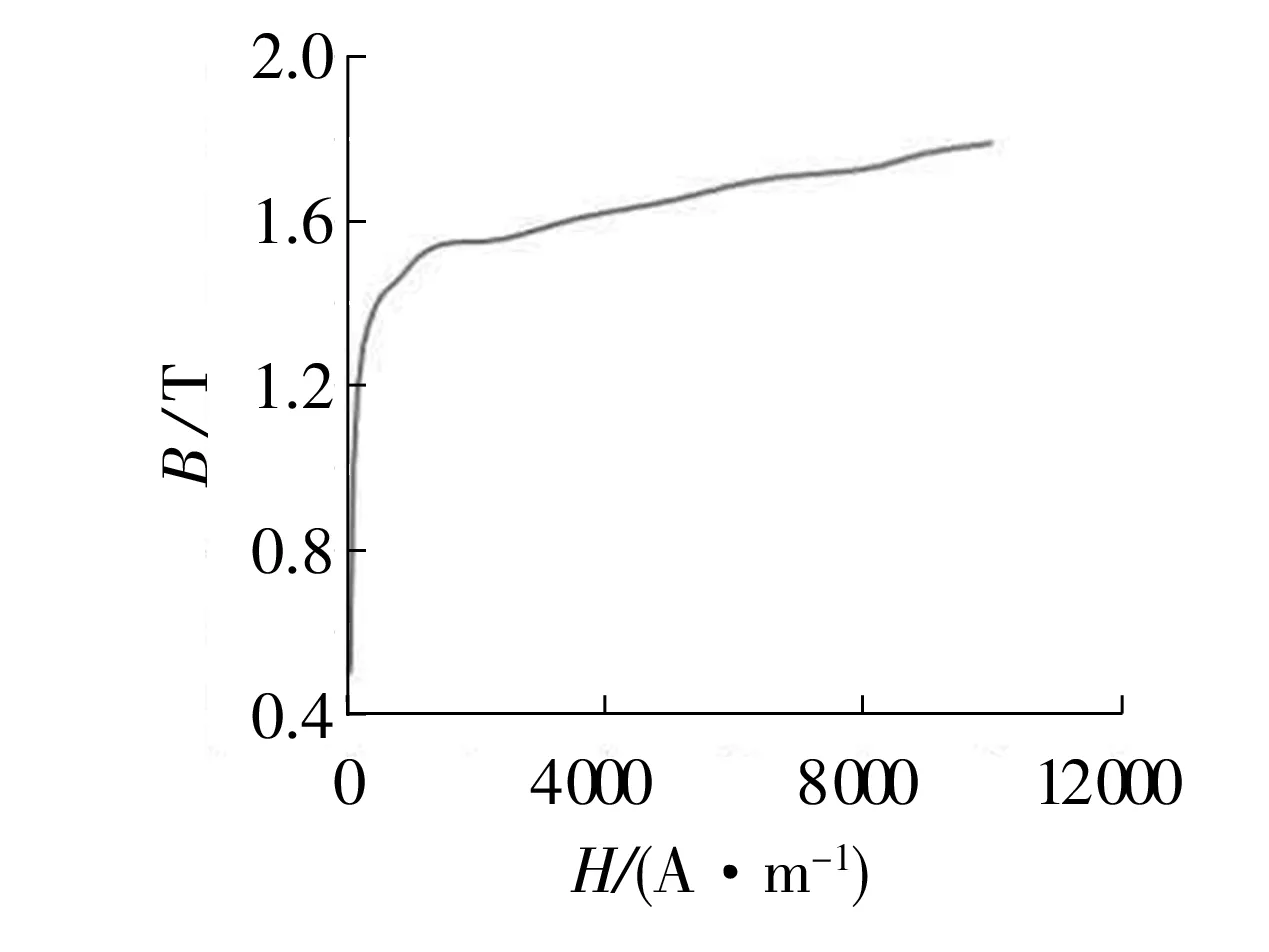
圖3 鐵磁材料B-H曲線圖Fig.3 B-H curve diagram of ferromagnetic material

圖4 ANSYS計算模型圖Fig.4 ANSYS calculation model
由于轉子在旋轉過程中的任何位置均可分解成x軸和y軸的位移,所以在分析耦合力的過程中只需研究沿x軸和y軸方向的分力,總耦合力在x軸的分力Fx=Fxx+Fyx,總耦合力在y軸的分力Fy=Fxy+Fyy。
3 理論和有限元計算結果分析
為了探究偏心距和電流同時作用對電磁力的耦合影響,分5種工況(表2)進行分析。每種工況中工作電流分別為1,2,3,4 A,轉子在x軸、y軸上的偏心距取值范圍為-0.3~0.3 mm,增量為0.1 mm。以直角坐標系x軸和y軸正方向為偏心距和耦合力的正方向。

表2 工況Tab.2 Operating conditions
3.1 工況1結果分析
給0和7這組磁極通電,當轉子沿x軸偏心時,轉子只受到x軸方向的電磁力,由(2)式可得Fxy=0,則Fx=Fxx,Fy=Fxy=0。在不同偏心距和工作電流下,Fx的理論和有限元計算結果對比如圖5所示,圖中It,Is分別為理論計算、數值模擬中所用的電流。
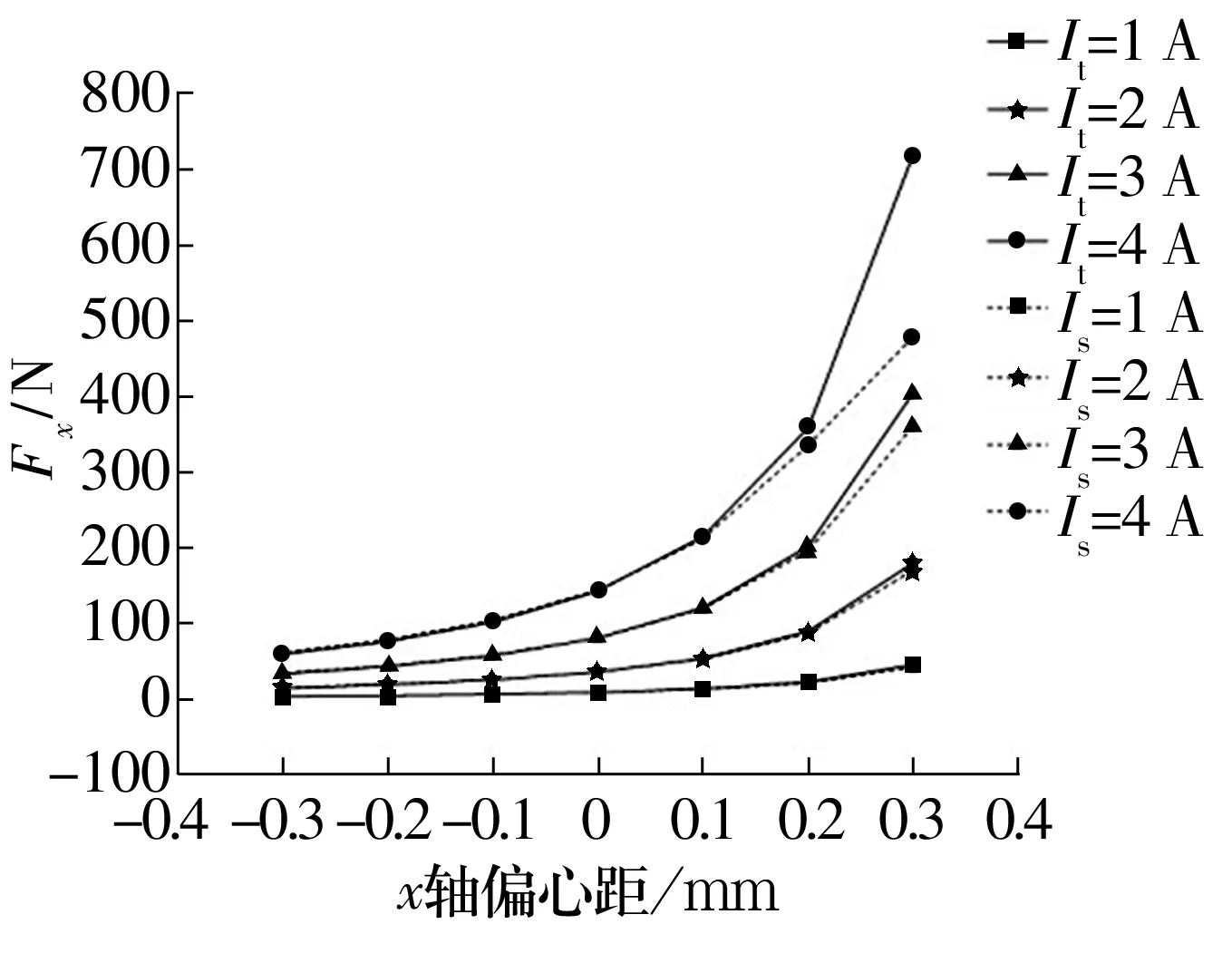
圖5 工況1不同電流下x軸偏心距與Fx的關系Fig.5 Relationship between x-axis eccentricity and Fx under different current in operating condition 1
由圖5可知,隨著轉子偏心距的增大,由于轉子逐漸靠近磁極0和7,轉子所受電磁力逐漸增大。偏心距在-0.3~0.2 mm內,理論值和數值模擬值吻合較好;偏心距在0.2~0.3 mm內,理論值和數值模擬值出現較大偏差,這是由于定子材料在磁化過程中存在磁飽和現象。當轉子逐漸靠近通電磁極0和7時,磁飽和現象越來越明顯,而在理論公式中,磁感應強度為定值。隨著電流增大,電磁力逐漸增大,且理論值和數值模擬值偏差也逐漸增大。主要因為電流增大,較小的偏心距使通電磁極達到磁飽和。理論值比數值模擬值大,主要因為數值模擬時存在少量的漏磁現象。

當轉子沿y軸偏心時,Fx=Fxx,Fy=Fxy。在不同偏心距和工作電流下,Fx,Fy的理論和有限元計算結果對比分別如圖6、圖7所示。
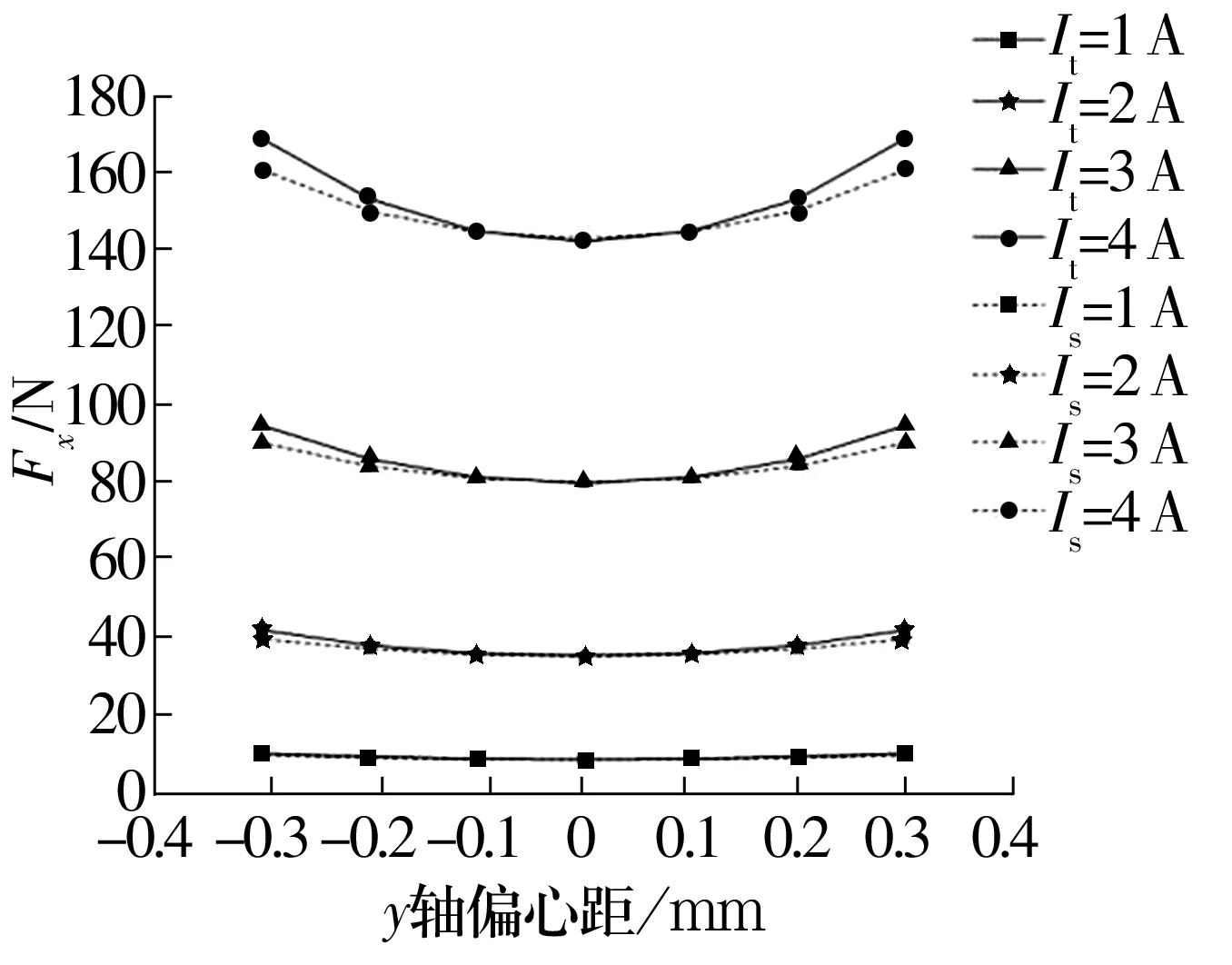
圖6 工況1不同電流下y軸偏心距與Fx的關系Fig.6 Relationship between y-axis eccentricity and Fx under different current in operating condition 1

圖7 工況1不同電流下y軸偏心距與Fy的關系Fig.7 Relationship between y-axis eccentricity and Fy under different current in operating condition 1
由圖可知,當轉子從-0.3 mm移動到0時,Fx,Fy的絕對值逐漸減小;當轉子從0移動到0.3 mm時,Fx,Fy的絕對值逐漸增大。當轉子在y軸正向和負向偏移相同距離時,Fx相等;當轉子在y軸正向和負向偏移相同距離時,Fy大小相等,方向相反。理論值和數值模擬值的偏差隨著轉子偏心距的增大而增大。圖6中轉子從-0.3 mm移動到0.3 mm過程中,每個偏心距下電流從1~4 A對應的平均誤差分別為5.35%,2.51%,0.67%,0.01%,0.67%,2.52%,5.35%。
3.2 工況2結果分析
給0和7,1和2這2組相鄰磁極通電,考慮磁極分布及轉子偏心的對稱性,只需分析轉子在x軸上偏心的情況。當轉子沿x軸偏心時,由于Fxy=0,則Fx=Fxx+Fyx,Fy=Fyy。在不同偏心距和工作電流下,Fx,Fy的理論和有限元計算結果對比分別如圖8、圖9所示。
由圖8可知,當轉子沿x軸正方向偏心時,Fx逐漸增大。由圖9可知,偏心距分別為-0.3,0.3 mm時,Fy的理論值相等,但數值模擬值不等。一方面是由于轉子靠近磁極0和7時,磁極逐漸達到磁飽和;另一方面是由于軸承的磁極是按照NNSS的形式布置的,磁極0和1的磁性是相同的,當這2組磁極通電時,磁極0和1之間存在微弱的相斥現象,導致磁極2處磁感應強度略大于磁極1處。

圖8 工況2不同電流下x軸偏心距與Fx的關系Fig.8 Relationship between x-axis eccentricity and Fx under different current in operating condition 2
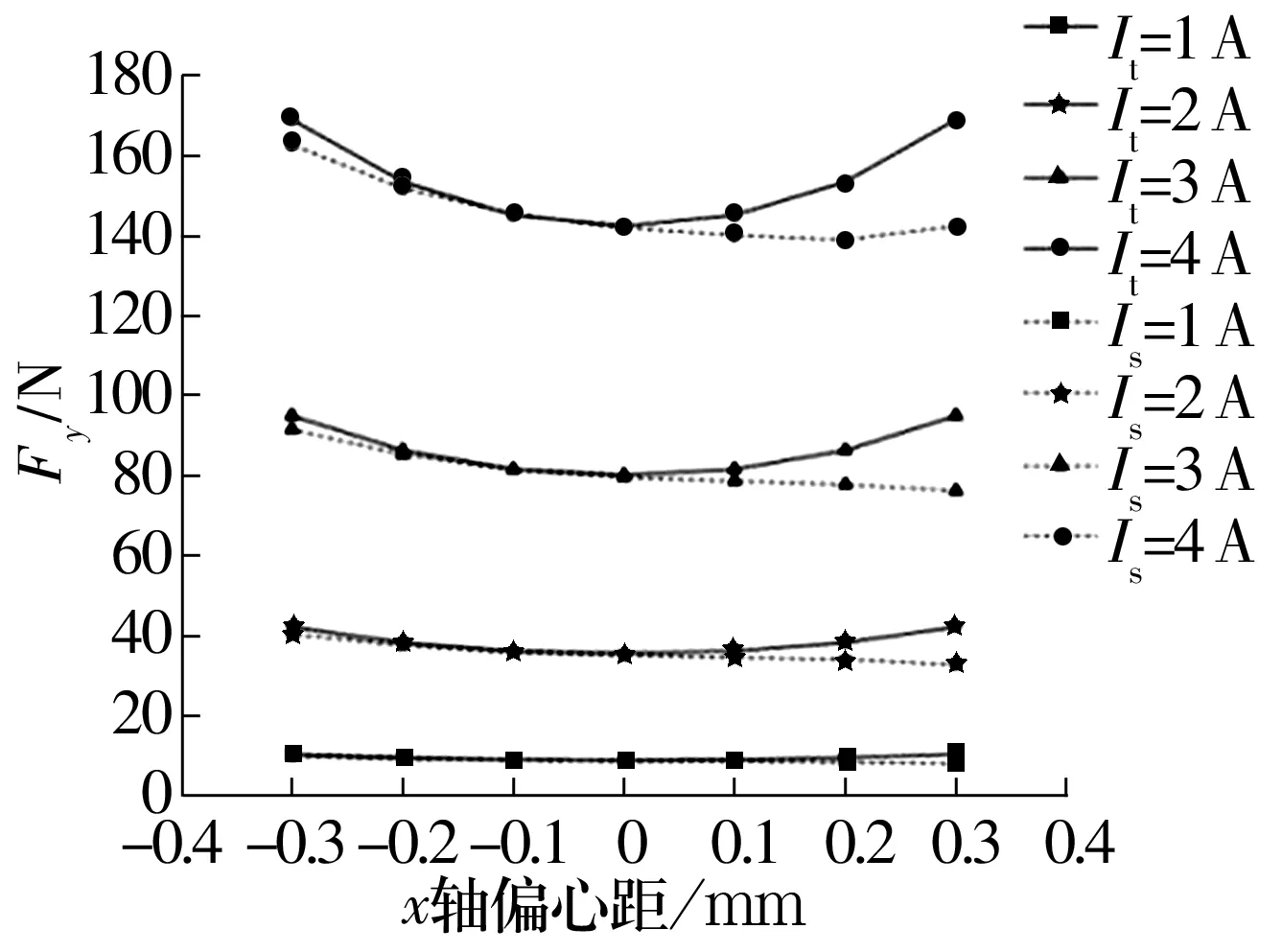
圖9 工況2不同電流下x軸偏心距與Fy的關系Fig.9 Relationship between x-axis eccentricity and Fy under different current in operating condition 2

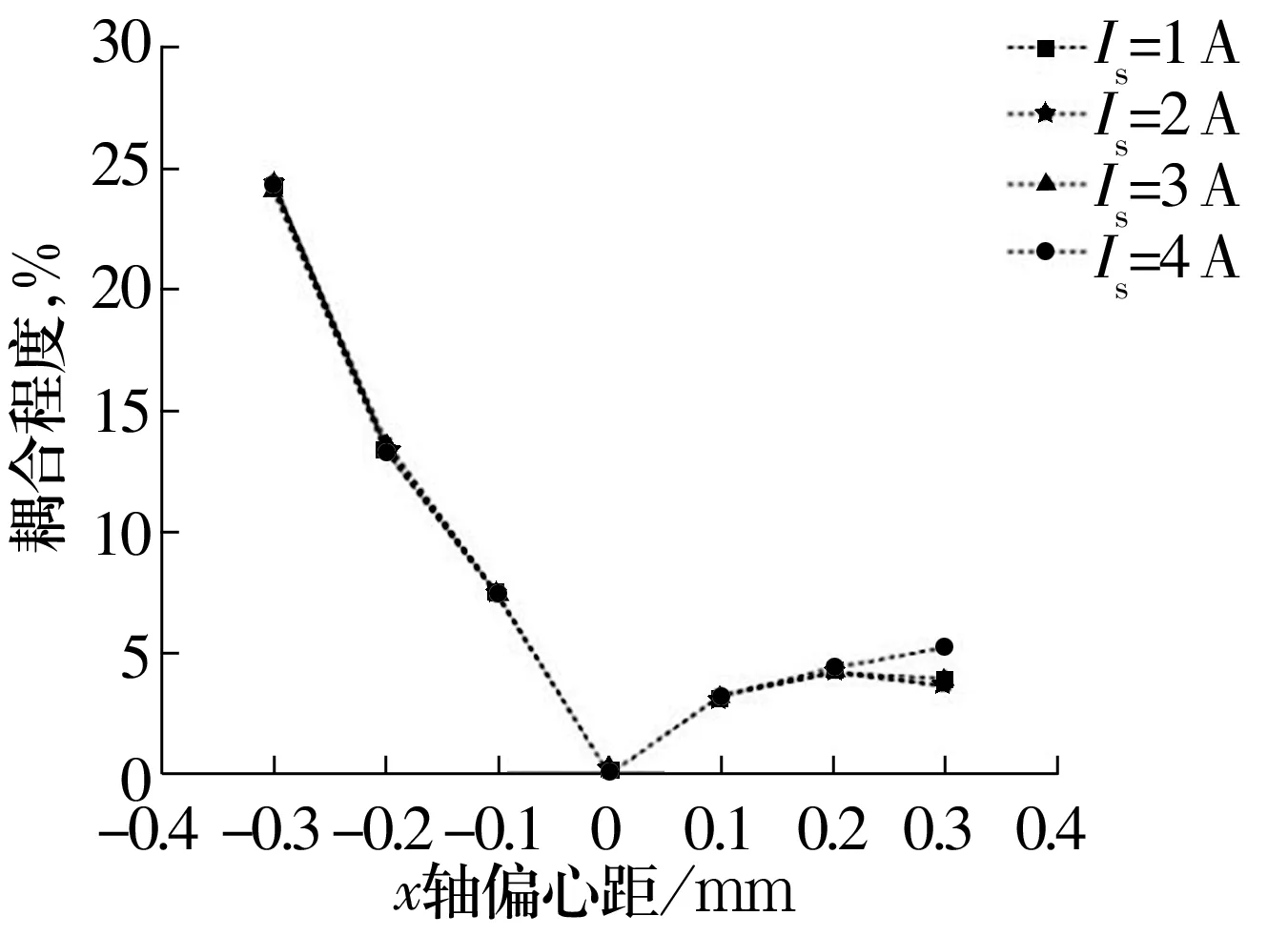
圖10 工況2不同電流下x軸偏心距與y通道對x通道耦合程度的關系Fig.10 Relationship between x-axis eccentricity and coupling degree of y channel to x channel under different current in operating condition 2
3.3 工況3結果分析
給0和7,3和4這2組相對磁極通電,當轉子沿著x軸偏心時,總耦合力在x軸上的分力Fx=Fxx,總耦合力在y軸上的分力Fy=Fxy=0。當轉子沿著y軸偏心時,總耦合力在x軸上的分力Fx=Fxx=0,總耦合力在y軸上的分力Fy=Fxy。Fx,Fy的理論和有限元結果對比分析分別如圖11、圖12所示。
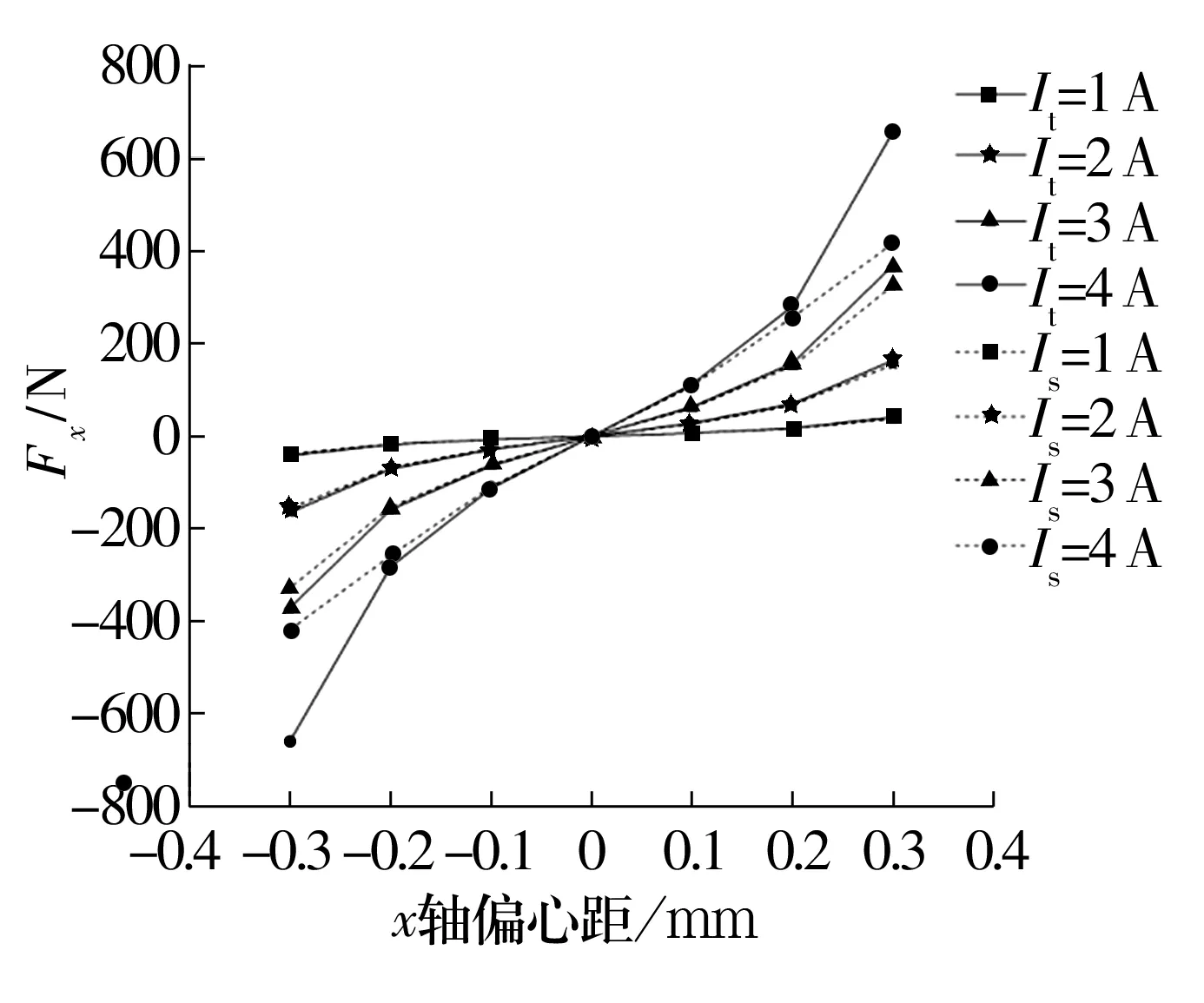
圖11 工況3不同電流下x軸偏心距與Fx的關系Fig.11 Relationship between x-axis eccentricity and Fx under different current in operating condition 3

圖12 工況3不同電流下y軸偏心距與Fy的關系Fig.12 Relationship between y-axis eccentricity and Fy under different current in operating condition 3
由圖可知,當轉子從-0.3 mm移動到0時,Fx,Fy的絕對值逐漸減小;當轉子從0移動到0.3 mm時,Fx,Fy的絕對值逐漸增大。轉子在y軸偏心時產生的耦合力Fy是給磁極0,7通電時Fy的2倍。圖11中轉子從-0.3 mm移動到0.3 mm的過程中,每個偏心距下電流從1~4 A的平均誤差分別為21.17%,5.83%,1.81%,0.04%,1.84%,5.84%,21.18%。
3.4 工況4結果分析
給0和7,1和2,3和4這3組磁極通電,當轉子沿x軸偏心時,由于Fxy=0,則Fx=Fxx+Fyx,Fy=Fyy,Fx,Fy的理論和有限元計算結果分別如圖13、圖14所示。工況4不同電流下x軸偏心距與y通道對x通道耦合程度的關系如圖15所示。當轉子沿y軸偏心時,Fx=0,Fy=Fxy+Fyy。Fy的理論和有限元計算結果對比如圖16所示。工況4不同電流下x軸偏心距與x通道對y通道耦合程度的關系如圖17所示。
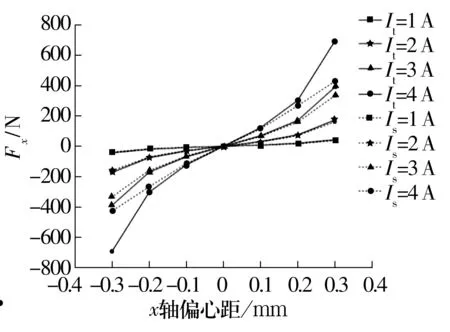
圖13 工況4不同電流下x軸偏心距與Fx的關系Fig.13 Relationship between x-axis eccentricity and Fx under different current in operating condition 4
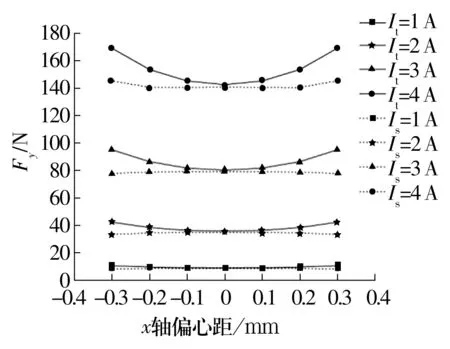
圖14 工況4不同電流下x軸偏心距與Fy的關系Fig.14 Relationship between x-axis eccentricity and Fy under different current in operating condition 4
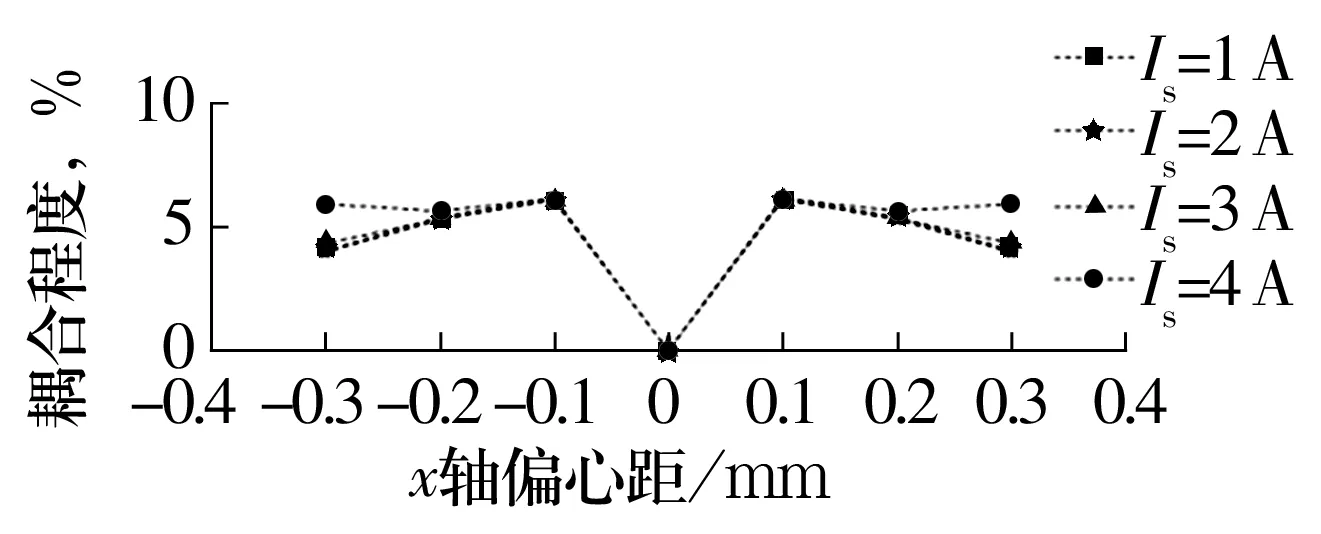
圖15 工況4不同電流下x軸偏心距與y通道對x通道耦合程度關系Fig.15 Relationship between x-axis eccentricity and coupling degree of y channel to x channel under different current in operating condition 4
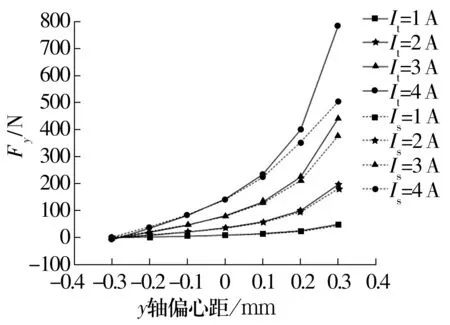
圖16 工況4不同電流下y軸偏心距與Fy的關系Fig.16 Relationship between y-axis eccentricity and Fy under different current in operating condition 4
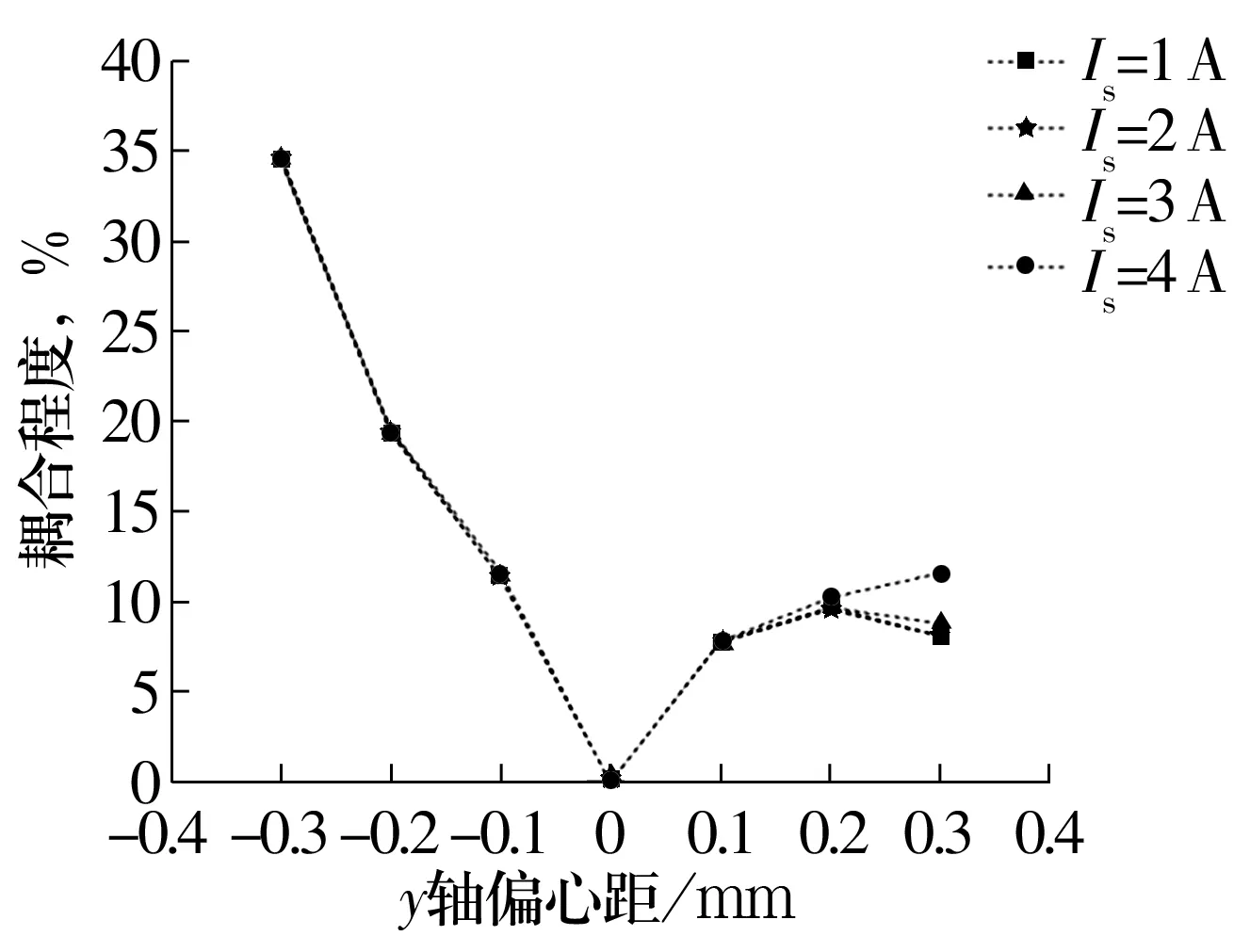
圖17 工況4不同電流下y軸偏心距與x通道對y通道耦合程度的關系Fig.17 Relationship between y-axis eccentricity and coupling degree of x channel to y channel under different current in operating condition 4
由圖13可知,當轉子從-0.3 mm移動到0時,Fx的絕對值逐漸減小;當轉子從0移動到0.3 mm時,Fx的絕對值逐漸增大。由圖14可知,Fy的理論值與數值模擬值變化趨勢不同,一方面是由于轉子靠近3和4或0和7這2組磁極時,被靠近磁極逐漸達到磁飽和;另一方面是由于軸承的磁極是按照NNSS的形式布置的,磁極0和1的磁性相同,磁極2和3的磁性相同,當這3組磁極通電時,磁極0和1,2和3之間存在微弱的相斥現象,導致磁極1,2外側的磁感應強度略小于內側。圖14中當轉子從-0.3 mm移動到0.3 mm的過程中,每個偏心距下電流從1~4 A的平均誤差分別為23.70%,10.57%,4.27%,2.33%,4.28%,10.62%,23.67%。
由圖16可知,當轉子偏心距為-0.3~0.3 mm時,由于轉子逐漸靠近磁極1和2,Fy逐漸增大;當偏心距為0.2~0.3 mm時,理論值和數值模擬值出現較大偏差,主要由于定子材料在磁化過程中存在磁飽和現象,當轉子逐漸靠近通電磁極1和2時,磁飽和現象越來越明顯,而理論公式中磁感應強度為定值。
3.5 工況5結果分析
給所有磁極通電,考慮磁極分布及轉子偏心的對稱性,只需分析轉子在x軸上偏心這一種情況。當轉子沿x軸偏心時,由于Fxy=0,Fyy=0,則Fx=Fxx+Fyx,Fy=0,Fx的理論和有限元計算結果如圖18所示。工況5不同電流下x軸偏心距與y通道對x通道耦合程度的關系如圖19所示。
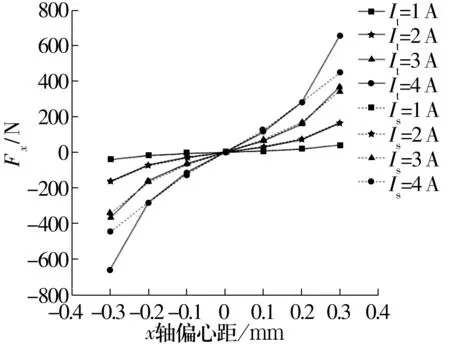
圖18 工況5不同電流下x軸偏心距與Fx的關系Fig.18 Relationship between x-axis eccentricity and Fx under different current in operating condition 5
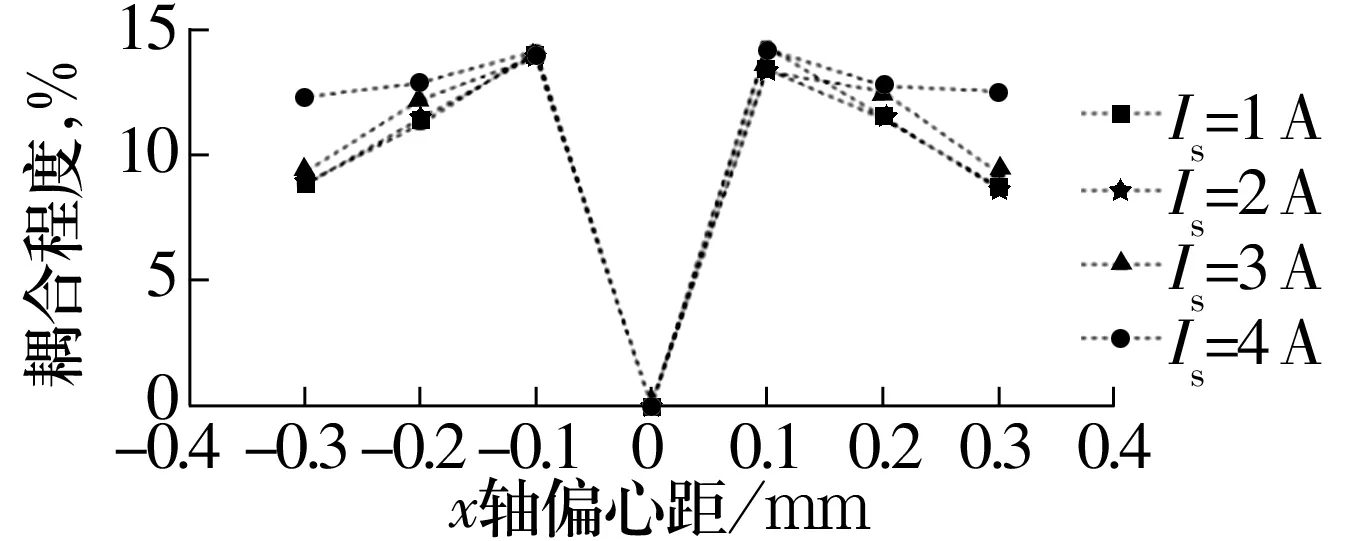
圖19 工況5不同電流下x軸偏心距與y通道對x通道耦合程度關系Fig.19 Relationship between x-axis eccentricity and coupling degree of y channel to x channel under different current in operating condition 5
由圖可知,當轉子偏心距為-0.3~0 mm時,Fx的絕對值逐漸減小;當轉子偏心距為0~0.3 mm時,Fx逐漸增大。理論值和數值模擬值的偏差隨著轉子偏心距的增大而增大。
3.6 小結
由圖5、圖8、圖11可知,相鄰磁極通電產生的耦合力的理論值較仿真值的相對誤差最大,相對磁極通電時耦合力相對誤差適中,一組磁極通電時最小,偏心距為0.2 mm時相對誤差分別為7.10%,5.84%和4.21%。
由圖6、圖9、圖14可知,通電磁極間存在耦合。只有一組磁極通電時,耦合力的相對誤差較小,偏心距為0.2 mm時只有2.52%。相鄰磁極通電時,在靠近通電磁極一側的相對誤差較大,偏心距為0.2 mm時其值達到11.62%。相對磁極通電時,磁極兩側的相對誤差均較大,偏心距為±0.2 mm時其值分別為10.62%,10.57%。
由圖10、圖15、圖17、圖19可知,工況1、工況3中x,y通道的耦合程度為0,工況2、工況4、工況5中不同電流大小對x,y通道的耦合程度幾乎沒有影響,只有在轉子靠近磁極時有差別,這是由于被靠近磁極達到磁飽和造成的。
4 結論
1) 偏心距越大,耦合力的理論值較仿真值的相對誤差越大。偏心距為±0.3 mm時,相對誤差為25%,理論公式不再適用;偏心距為-0.2~0.2 mm時,相對誤差基本小于10%,理論值和仿真值吻合較好。
2) 耦合力隨工作電流的增大而增大,且理論值較仿真值的相對誤差逐漸增大。當偏心距相同時,磁極達到飽和前,電流大小對通道間的耦合程度幾乎沒有影響;達到飽和后,不同電流大小對應的通道間耦合程度有所不同。
3) 磁極對通電情況對通道間耦合程度的影響較為顯著。偏心距為0.2 mm時,相鄰磁極、相對磁極和一組磁極通電產生耦合力的理論值較仿真值的相對誤差分別為6.03%,5.14%和4.21%。

