基于相關系數原理EMD的轉子故障特征提取方法研究

呂世鵬

（新疆大學 機械工程學院，烏魯木齊 830047）

轉子系統是常見的機械傳動形式和核心部件，轉子的故障診斷方法一直是機械可靠性研究領域的熱門及重點之一。信號時頻分析方法的性能和對故障特征的提取效果直接決定故障診斷的品質。傳統的分析方法如Wigner-Ville時頻分布和小波變換等方法隨著應用領域的擴展和研究的深入開始暴露出不足之處[1]。為此，人們提出了新的信號時頻分析方法經驗模態分解（EMD），它解決了傳統時頻分析方法的線性和自適應性分析問題。本文在試驗實例中，運用EMD方法對碰磨故障的轉子振動信號進行分解分析，利用相關系數原則來加強EMD方法本身的降噪濾波特性，對分解產生的本征模態函數（IMF）進行篩選降噪處理并分析其時頻特征，使得特定故障特征清晰化，進而完成特征提取[2]。

1 EMD方法

EMD方法是一種自適應分解方法，為了能將信號表達為一系列代表信號內包含的各個成分的分量之和，IMF被定義出來。類似于傅里葉變換，可以將信號表達為正交的弦函數序列之和，IMF也需要滿足一定的條件才具有數學和物理意義：可以滿足包絡計算的極值點數量和局部包絡均值為零。這兩個條件也是為EMD的分解步驟而設定的。

將一個信號通過EMD方法分解為IMF序列之和，需要先提取信號的極值點，以極值點為基點使用三次樣條插值法構造信號包絡線；用構造的上、下包絡線計算出包絡均值數據序列，該序列代表了信號的靜態成分；期望得到的有振動成分代表意義的IMF在濾去該靜態成分的信號中，即用于原信號數據序列與包絡均值的求差結果中；得到的分量繼續作為原始信號進行上述分解過程，其中若有分量滿足IMF定義條件判斷，即為IMF主分量，后續重復計算判斷得到其他IMF分量[3]。若出現所得分量無法滿足分解計算條件（成為單調函數）則分解結束，原始信號可以表達為：

式中，ci（t）為分解出的第i個IMF分量；r（t）為余項分量。

2 基于相關系數原理的EMD降噪及特征提取

實際上，IMF分量并不都是具有單一物理意義的，噪聲的干擾會造成分解篩選過程出現模態混疊及虛假分量。為找出這些無關分量，降低或消除噪聲的干擾，人們通過能反映函數序列的關聯程度的數值參數作為指標準則來進行篩選識別。

相關系數的計算過程為：

式中，ρi為第i個IMF分量與原信號的相關系數，取值范圍為0到1，N為采樣點數量。

IMF分量根據分解順序應按照主成分到無關成分的趨勢排列，故從整體上相關系數變化應呈較小的趨勢。然后，判斷含有無關噪聲成分的分量和虛假分量從何階開始出現，需要以相關系數作為參考閾值。本文取一次分解所有IMF分量中的最大相關系數的十分之一為參考。

3 試驗分析

試驗分析驗證實例為：使用美國Bently公司RK-4轉子故障試驗平臺進行故障試驗，采集振動信號對提出方法的效果進行驗證。設置采樣頻率為1024Hz，轉速4000r/min，轉頻66Hz。分別采集正常運行和碰磨故障情況下兩組實信號，如圖1所示。

圖1 采樣信號

從時域圖譜可以看出，故障程度較嚴重，但無法提取故障對用的特征。對故障采樣信號進行EMD方法處理，可得到7項IMF分量以及一項余項，根據式（2）分別計算8項分解結果的相關系數，如表1所示。

可以看出，篩選閾值約為0.068，保留前三階分量即IMF1～IMF3，如圖2所示。

保留的IMF分量是振動的主要成分，濾去了虛假分量和無關噪聲成分。此時，用保留IMF分量重構信號，如圖3所示。對重構信號進行頻域分析，對比IMF主要分量和正常振動信號的頻率特征，如圖4所示，可以對碰磨故障的振動特征進行提取。

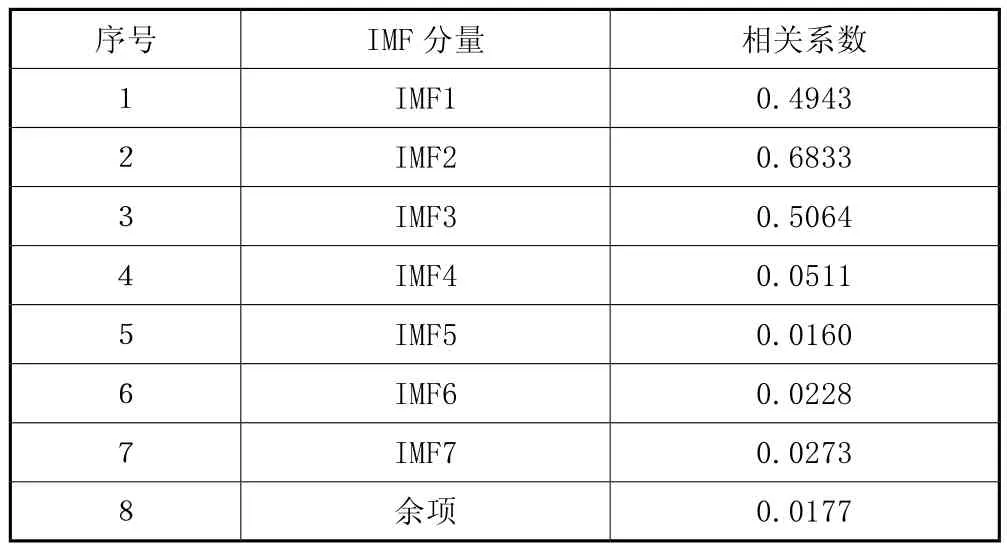
表1 8項分解結果的相關系數

圖2 前三階分量

圖3 重構信號

圖4 頻域幅值譜對比

碰磨故障對轉子系統產生的振動沖擊頻率應該基本和轉頻一致或者是其倍頻。實際從頻譜上分析時，從圖4（a）中可以看出，主頻特征是2倍頻和30倍頻，而碰磨故障信號的頻譜首先出現了以1倍轉頻和15倍頻為中心的頻帶成分，其次這些頻帶成分是以轉頻為帶寬。所以，主頻成分的半頻效應和以主頻的半頻頻率為中心的頻帶帶寬可作為碰磨故障的特區特征。

4 結語

通過提出一種基于相關系數原理EMD的特征提取方法，在試驗驗證下，筆者最終得出以下結論：分析EMD方法對信號進行自適應尺度分解的原理后，在合適的篩選條件下，該方法具有良好的濾波消噪基礎；將相關系數作為閾值引入EMD方法中，可以起到很好的消噪效果，能夠提取出轉子碰磨故障的特征；EMD作為故障診斷領域提出時間較晚的方法，還有很大的發展活力，對比分析更多的故障特征頻譜信息，故障特征提取的準確性可以進一步提升和驗證。