49MnVS3非調質鋼的兩種軋制力模型對比

， ， ， ， ，

(西安建筑科技大學冶金工程學院，西安 710055)

0 引 言

隨著計算機技術在熱軋生產過程中的廣泛應用，現代化軋鋼的生產流程已向自動化、高速化和優質化方向發展[1]。在棒線材軋制過程中，變形抗力和軋制力的準確計算對于保證軋制規程的順利進行是非常重要的[2]。軋制力是指軋件變形時作用于軋輥上總壓力的垂直分量，研究軋制過程中接觸弧上單位軋制壓力的分布規律對準確確定軋制力有重大意義。正確預測軋制力的大小不僅可以合理使用設備和安排軋制規程，還能減少設備損耗和節約生產成本，而平均單位軋制壓力與金屬的變形抗力直接相關[3-5]。棒線材生產過程中各環節的溫度變化、軋制工藝的制定以及產品質量的控制等，都將直接影響最終軋制工藝的穩定性和生產的精確性，并需要精確的數學模型對軋制過程進行控制，從而獲得更高精度的產品[6-8]。此外，金屬的熱變形抗力對于軋制工藝的制定和軋機設備的選擇是必不可少的[9-10]。因此，建立能正確反映金屬材料力學性能參數與熱變形工藝參數關系的數學模型，可實現軋制過程的計算機模擬，從而達到優化熱軋工藝和進一步提高材料力學性能的目的。熱軋軋制力計算模型主要有艾克隆德模型、周紀華-管克智變形抗力模型等。周紀華-管克智變形抗力模型通過擬合的軋制力計算出單位軋制壓力，這需要大量的試驗數據進行擬合；而艾克隆德模型以理論和試驗數據為基礎建立了計算平均單位軋制壓力的半經驗公式[2,7,11-12]。曲軸用49MnVS3鋼是一種中碳、釩微合金化含硫非調質鋼，具有高韌性、易切削、力學性能與中碳調質鋼的相當或更優異等特點，同時其生產中無需淬火、回火、校直、消除應力回火等工序，可節約能源，有“綠色鋼鐵”之稱[13-15]。為了給49MnVS3非調質鋼的軋制工藝設計提供準確的軋制力計算方法，作者分別采用周紀華-管克智變形抗力模型和艾克隆德模型計算了該鋼在棒材軋制過程中各機組不同道次的平均單位軋制壓力，并進行了比較。

1 試樣制備與試驗方法

試驗材料為49MnVS3非調質鋼，由西寧特殊鋼股份有限公司提供，其化學成分見表1。將試驗鋼加工成尺寸為φ10 mm×15 mm的試樣，在Gleeble-3500型熱模擬試驗機上進行單道次熱壓縮試驗，變形溫度為750，800，850，900，950，1 000 ℃，應變速率分別為0.1，1，10，50 s-1，變形量為60%(真應變為0.92)，變形結束后立即水冷至室溫。在試驗過程中同步采集真應力和真應變數據，得到真應力-真應變曲線。

試驗鋼在棒材連軋生產線上軋制時19個機架的孔型系統和軋制工藝參數見表2。

表1 49MnVS3非調質鋼的化學成分(質量分數)Tab.1 Chemical composition of 49MnVS3 non-quenchedand tempered steel (mass) %

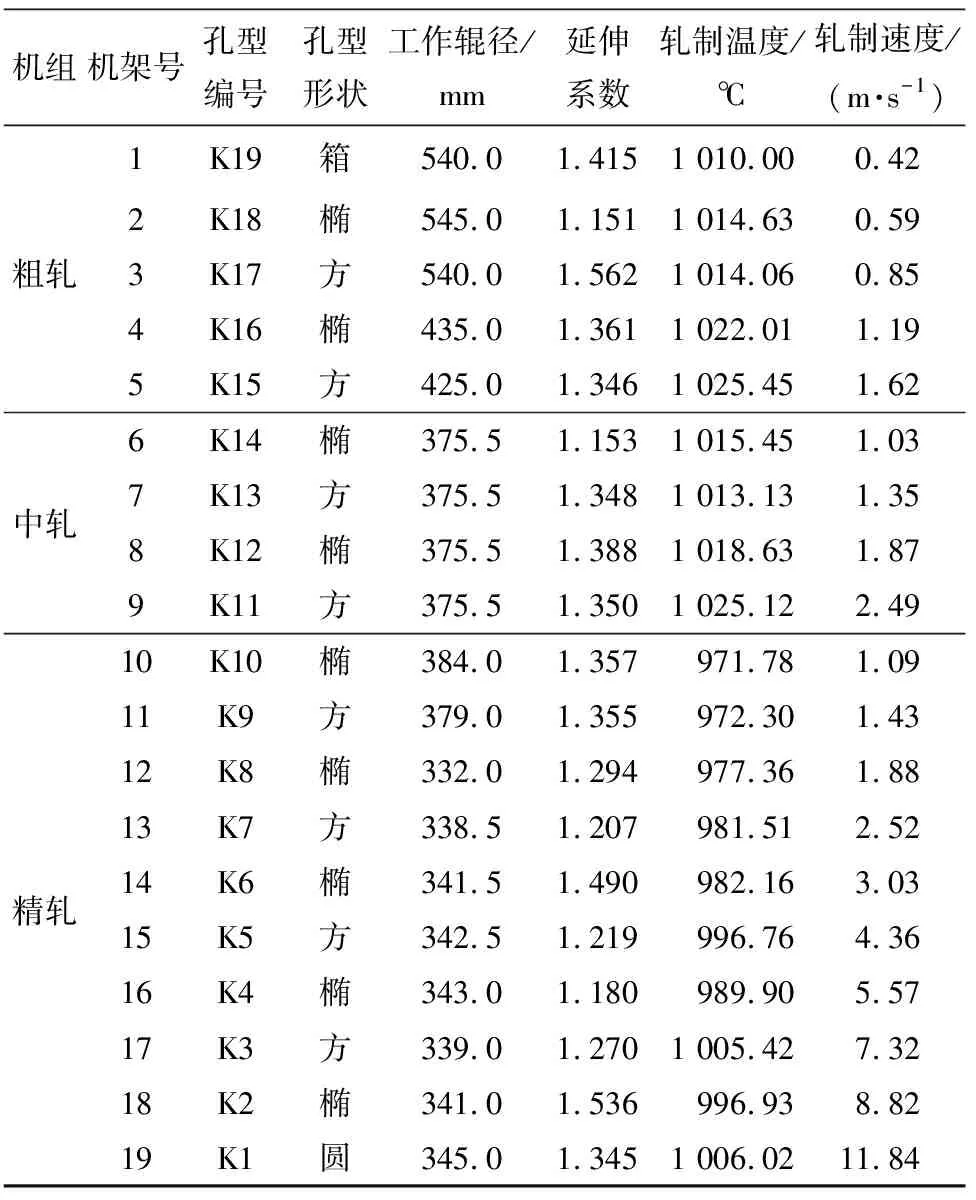
表2 棒材連軋生產線的孔型系統和試驗鋼的軋制工藝參數Tab.2 Pass sequence of continuous rod production line androlling process parameters of tested steel

2 試驗結果與討論

2.1 真應力-真應變曲線

由圖1可知：在不同變形溫度下試驗鋼的真應力均隨著應變的增加先增大后趨于穩定；當應變速率一定時，真應力隨著變形溫度的升高而降低；當變形溫度一定時，真應力隨應變速率的增加而增大；在變形溫度為750 ℃，應變速率為50 s-1條件下，試驗鋼的真應力峰值達到400 MPa左右。

2.2 周紀華-管克智變形抗力模型的建立

周紀華-管克智變形抗力模型的計算公式為

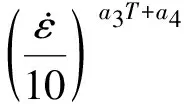
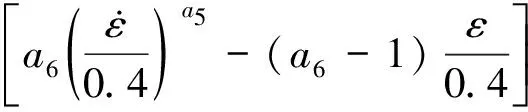
(1)

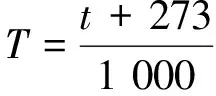
(2)

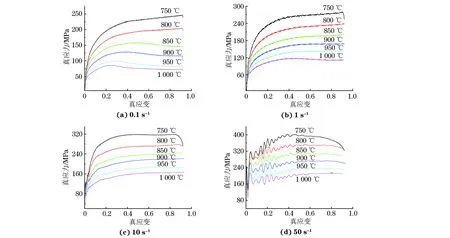
圖1 不同變形溫度和應變速率下試驗鋼的真應力-真應變曲線Fig.1 Ture stress-true strain curves of the tested steel at different deformation temperatures and strain rates

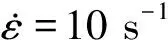
用Origin軟件對圖1中不同變形溫度和應變速率下的真應力與真應變進行非線性回歸分析，擬合得到試驗鋼變形抗力模型中的回歸系數和基準變形抗力，如表3所示。

表3 擬合得到試驗鋼周紀華-管克智變形抗力模型的回歸系數和基準變形抗力Tab.3 Regression coefficient and reference deformation resistance of Zhou Jihua-Guan Kezhi deformation resistancemodel of the tested steel after fitting

將回歸系數和σ0代入式(1)得到：

σ=157exp(-2.860 25T+

(3)

2.3 平均單位軋制壓力模型的對比

以孔型K5、K4為例，根據表2的孔型系統和軋制工藝參數計算平均單位軋制壓力。

基于艾克隆德模型，平均單位軋制壓力的計算公式[7]為

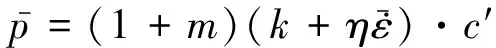
(4)

c′=0.968 2+0.006 56v

(5)

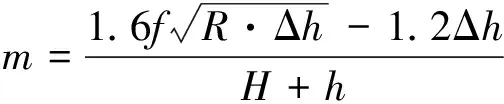
(6)

k=10×(14-0.01t1)×

[1.4+w(C)+w(Mn)+w(Cr)]

(7)

f=a(1.05-0.000 5t1)

(8)

η=0.1(14-0.01t1)c

(9)

表4 軋制速度影響系數Tab.4 Influence coefficient for rolling speed

將表2和表4中的數據代入式(4)～式(9)，得出K5孔入K4孔時的基于艾克隆德模型的平均單位軋制壓力為221.31 MPa，采用同樣的計算方法得到其他道次的平均單位軋制壓力列于表5中。

基于周紀華-管克智變形抗力模型，平均單位軋制壓力的計算公式[2]為

(10)

式中：nσ為應力狀態影響系數。

(11)

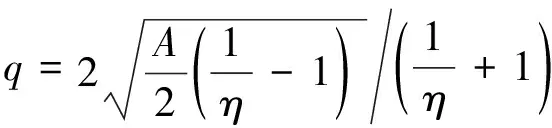
(12)

ak=Bk/H

(13)

A=D*/H

(14)

式中：q為變形區形狀參數；ak為孔型軸比；A為軋輥轉換直徑，mm；Bk為軋輥寬度，mm；D*為軋輥孔型槽底直徑，mm。

將表2中的數據代入式(11)～式(14)，得到nσ為1.54，然后代入式(10)求得K5孔入K4孔時的基于周紀華-管克智變形抗力模型的平均單位軋制壓力為178.54 MPa，采用同樣的計算方法得到其他道次的平均單位軋制壓力如表5所示。

由圖2和表5可知：隨著軋制道次的增加，即應變的增加，基于艾克隆德模型和周紀華-管克智變形抗力模型計算得到的平均單位軋制壓力均增大；基于艾克隆德模型得到的平均單位軋制壓力曲線波動較小，而基于周紀華-管克智變形抗力模型，通過熱模擬試驗結果擬合得到的平均單位軋制壓力曲線波動較大，這是由于變形程度對基于周紀華-管克智變形抗力模型得到的軋制力的影響比較大而造成的；在低應變速率(粗軋、中軋與預精軋階段)下，基于艾克隆德模型計算得到的平均單位軋制壓力較大，而在高應變速率(精軋階段)下，基于周紀華-管克智變形抗力模型計算得到的平均單位軋制壓力較大，這主要與高應變速率引起的形變強化、溫升效應及動態再結晶等因素有關。

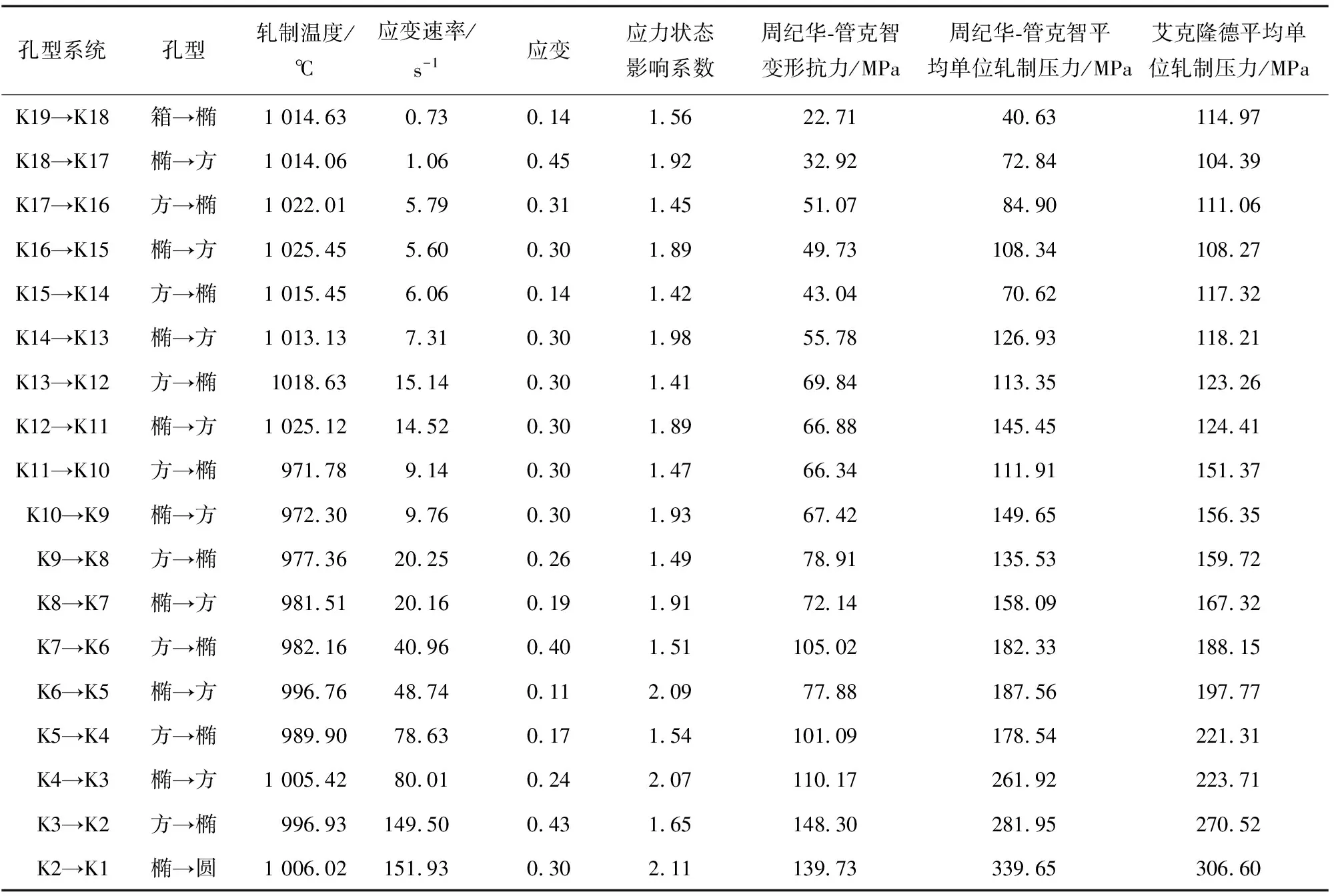
表5 基于兩種模型計算得到的平均單位軋制壓力Tab.5 Calculated average unit rolling prossures on basis of two models

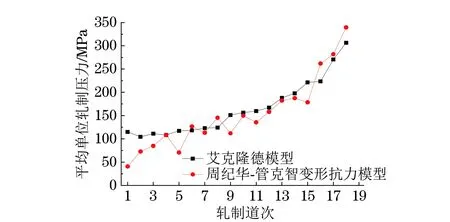
圖2 基于兩種模型得到的平均單位軋制壓力的對比Fig.2 Comparison of average unit rolling forces obtained on basis of two models

基于周紀華-管克智變形抗力模型計算平均單位軋制壓力時，需要借助熱模擬試驗得到的數據，因此不同軋制道次的變形量對其影響很大，該模型接近于實際生產情況，適用于控制模型；而艾克隆德模型通過材料的化學成分和軋制工藝參數來計算平均單位軋制壓力，因此其在實際設計中的應用更加廣泛，該模型適用于軋制工藝設計。

3 結 論

(1) 隨著軋制道次的增加，即應變的增加，基于艾克隆德模型和周紀華-管克智變形抗力模型計算得到的平均單位軋制壓力均增大；基于艾克隆德模型得到的平均單位軋制壓力曲線波動較小，而基于周紀華-管克智變形抗力模型的波動則較大；在低應變速率(粗軋、中軋與預精軋階段)下，基于艾克隆德模型計算得到的平均單位軋制壓力較大，而在高應變速率(精軋階段)下，基于周紀華-管克智變形抗力模型計算得到的平均單位軋制壓力較大。

(2) 基于周紀華-管克智變形抗力模型計算軋制力時，需要借助熱模擬試驗得到的數據，該模型適用于控制模型；艾克隆德模型只需使用化學成分和軋制工藝參數即可計算平均單位軋制壓力，應用更廣泛，該模型適用于軋制工藝設計。