橡膠材料的混合高彈性本構模型研究

于海富，李凡珠，楊海波，張立群

（北京化工大學 有機無機復合材料國家重點實驗室，北京 100029）

橡膠材料因其良好的高彈性廣泛應用于社會生產，同時利用計算機模擬手段表征橡膠制品的力學性能已得到越來越多人的認可[1]。因此橡膠材料高彈性本構方程的研究具有重大意義。對橡膠材料高彈性的理論研究通常可分為唯象理論和統計理論兩部分[2]。唯象理論是基于應變不變量或拉伸比得到應變能函數。基于應變不變量的典型模型包括Mooney-Rivlin模型[3]、Yeoh模型[4]和Gent-Thomas模型[5]等，基于拉伸比的典型模型包括Valanis-Landel模型[6]和Ogden模型[7]等。基于唯象理論的本構模型已有很多研究[8-10]。統計理論則由橡膠材料的微觀結構出發，由分子鏈網絡構象熵的變化得到自由能的關系，進而與宏觀層面的拉伸比建立聯系，得到最終的本構模型。依據橡膠分子鏈末端距的徑向分布函數是否符合Gaussian函數，可將統計模型分為Gaussian鏈網絡模型和非Gaussian鏈網絡模型[11]。典型的非Gaussian鏈網絡模型有3-鏈網絡模型[12]、4-鏈網絡模型[13]和8-鏈網絡模型[14]等。相比于3-鏈網絡模型和4-鏈網絡模型只能描述單一變形模式下的力學行為，8-鏈網絡模型能較好地描述不同變形模式下的力學行為。雖然非Gaussian鏈網絡模型能夠預測大變形情況，但是在小變形下的預測能力較差。因此，近年來出現了混合本構模型。P.D.Wu等[15]提出了以3-鏈網絡模型和8-鏈網絡模型的線性組合來替代全網絡模型，A.Elías-Zuniga等[16]進一步修正了該模型，但上述混合模型的基礎是兩個非Gaussian統計模型。

本工作采用修正Gaussian鏈網絡模型與修正8-鏈網絡模型的非線性組合，建立了一種新的混合本構模型。

1 本構理論

1.1 混合本構模型

對于橡膠材料，其高彈性可認為是熵彈性，即由于構象熵的變化所導致[17]。對Gaussian鏈網絡模型而言[2，11]，其單位體積構象熵（ΔSG）的表達式如下：

式中，n為分子鏈網絡的分子鏈密度，k為Boltzmann常數，λi（i=1，2，3）為拉伸比。

對于8-鏈網絡模型[2，14，16]，其單位體積構象熵（ΔSN）的表達式如下：

式中，c為常數，N8為鏈段數，λr為相對鏈伸長，β為Langevin函數L（β）的逆函數，即：λr＝L（β）＝cothβ-β-1。

橡膠材料的變形在統計理論上主要反映在微觀和宏觀兩個層面。微觀層面主要取決于構象熵，本工作主要考察單位體積分子鏈的數目（即n）的影響。而反映在宏觀層面上，則主要考察λ的影響。

由于將變形分解為Gaussian變形部分和非Gaussian變形部分，因此微觀層面上的n也分為兩部分。定義函數φ表示n中非Gaussian部分所占比例，函數關系如下：

式中，b為常數，Im為非Gaussian變形部分所主導的范圍。

Im與最大應變量（εmax）的關系如下：

式中，d為常數，且d＞0。

將宏觀層面上的λ同樣分解為Gaussian變形和非Gaussian變形兩部分，定義函數ρ表示非Gaussian變形部分所占比例。考慮到橡膠材料處于小變形或大變形條件下時，分子鏈的變形狀態分別趨近于Gaussian變形和非Gaussian變形，因此函數ρ采用如下形式：

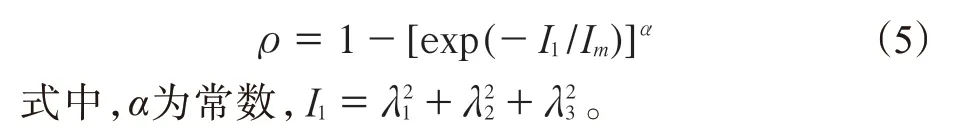
由式（1）及（3）—（5）可得到混合模型中單位體積Gaussian變形部分的ΔSG：

由式（2）—（5）得到單位體積非Gaussian變形部分的ΔSN：

由以下構象熵（ΔS）與自由能（W）的關系式（T為溫度）[18]：

可分別得到Gaussian變形和非Gaussian變形兩部分的自由能函數：

式中，w0為常數，μ＝nkT。

對Langevin函數的逆函數而言，不能找到它的閉型，故采用其近似式[19]，函數形式如下：

因此，混合模型的自由能函數為：

1.2 加載條件

橡膠材料通常被認為是不可壓縮材料，主拉伸方向上Cauchy應力（σi）與自由能的關系如下[20]：

式中，p為靜水壓力，I為應變不變量，i＝1，2，3。

在橡膠材料的力學性能測試中，常用到的加載模式主要有單軸拉伸（UT）、平面拉伸（PT）和等雙軸拉伸（ET）[21]。因此，通過式（12）和（13）針對不同加載條件可得到相應的Cauchy應力：

2 試驗數據擬合

應用本工作提出的混合本構模型，對炭黑填充天然橡膠（NR）的試驗數據和文獻數據（Treloar數據[17，22]）進行擬合驗證。

2.1 試驗配方和數據擬合

試驗配方：NR 100，炭黑 40，氧化鋅 3，硬脂酸 1，硫黃 1，促進劑CZ 1.5。制備不同拉伸模式下的試樣，消除試樣的Mullins效應[23]后進行測試。對于UT，PT和ET測試，均保持100%的最大應變條件，試驗結果如圖1所示。

圖1 單軸拉伸、平面拉伸和等雙軸拉伸的試驗數據

利用本構模型式（14）—（16）將UT，PT和ET三組數據同時進行擬合，得到一組共同的本構參數，見表1。

表1 不同模型擬合試驗數據的本構參數

應用Gaussian模型、3-鏈網絡模型和8-鏈網絡模型，以相同的方法進行數據擬合，并與混合本構模型的擬合效果進行對比。

混合本構模型及其他本構模型的數據擬合結果如圖2所示。由圖2可見，混合本構模型的整體擬合效果較好，初步說明該模型的正確性。雖然混合本構模型對ET數據的擬合不是很理想，但是相比其他3個模型已得到改善，且整體擬合效果有了較大改進。

圖2 4種模型的擬合數據與試驗數據對比

2.2 與Treloar 數據對比

Treloar數據能夠很好地表現3種拉伸方式間的關系，通常用來檢驗本構模型對3種拉伸方式的預測能力。為進一步檢驗混合本構模型的準確性，使用Treloar數據（見圖3）進一步驗證。

圖3 Treloar數據的單軸拉伸、平面拉伸和等雙軸拉伸曲線

以Treloar數據為基礎，采用相同方法分別使用混合本構模型、Gaussian模型、3-鏈網絡模型和8-鏈網絡模型進行數據擬合，得到相應的本構參數（見表2），擬合結果見圖4。

表2 不同模型擬合Treloar數據的本構參數

由圖4可見，混合本構模型具有較好的擬合效果，相比其他3個模型，擬合精度大幅提高。

圖4 4種模型的擬合數據與Treloar數據對比

3 結論

基于分子統計理論提出了一種適用于橡膠材料的混合高彈本構模型，采用修正Gaussian模型和修正8-鏈網絡模型的非線性組合分別描述Gaussian變形和非Gaussian變形部分。微觀層面上主要考察分子鏈密度，并將其分解為Gaussian變形和非Gaussian變形部分，并定義了表示非Gaussian部分所占比例的函數；宏觀層面上的拉伸比也分解為兩部分，并建立了非Gaussian部分的比例函數。由Gaussian變形和非Gaussian變形部分的構象熵變化得到構象熵變化之和，再由構象熵與自由能的關系，得到混合本構模型。該混合本構模型含有5個參數（μ，N8，α，b，d），通過同時對UT，PT和ET三組數據擬合得到。通過試驗數據和文獻數據（Treloar數據）的擬合對比，初步證明了該混合本構模型的適用性。與Gaussian模型、3-鏈網絡模型和8-鏈網絡模型相比，混合本構模型在精確性方面有明顯提高。