表面缺陷對硅橡膠密封性能的影響規律研究

吳 健，董吉義，Bipin Kumar Gond，王友善，粟本龍，崔志博

[1.哈爾濱工業大學（威海） 橡膠復合材料與結構研究所，山東 威海 264209；2.印度理工學院坎普爾校區，印度 坎普爾208016]

硅橡膠密封件是保證設備正常運轉的關鍵零件，以其優異的物理和化學性能在航空航天領域應用廣泛。由于加工精度、復雜工作環境及裝配工藝等的影響，在長期使用過程中密封界面容易出現表面缺陷。而密封件上任一微小的表面缺陷都極易導致泄漏，進而致使整條密封帶失效，造成嚴重損失。因此，研究表面缺陷對密封性能的影響尤為重要。

近年來，國內外學者針對表面形貌對密封性能的影響做了較多研究。Y.Matsuzaki等[1]基于硬質球與軟質錐形密封面的接觸建立密封面接觸模型，并通過試驗研究了不同粗糙表面泄漏量的變化規律。P.Wagner等[2]基于功率譜密度分解理論建立了橡膠接觸模型的多尺度有限元分析方法，從宏觀和微觀角度研究了橡膠在粗糙表面的接觸特性。陳國定等[3]利用有限元分析軟件MARC/MENTAT 320針對不同粗糙峰形貌對密封性能的影響進行了研究，得出了靜態接觸下密封件陷入粗糙谷中的位移量隨粗糙峰結構和波長尺寸的變化規律。王國志等[4]利用ANSYS軟件分析了水壓O形圈在不同粗糙表面下密封表面接觸間隙的變化規律，并采用FLUENT軟件進行微流場仿真，得到了O形圈的最小接觸寬度。蔡艷等[5]通過實際測量漏油和不漏油的油泵零件各個表面粗糙度參數，揭示了輪廓的支承長度率對密封性能的影響。但是，現有文獻主要側重于研究表面粗糙度對密封性能的影響，對于密封界面表面缺陷的研究也只集中在表面缺陷的檢測上[6-8]，而針對表面缺陷對密封性能影響的研究卻鮮有報道。T.J.Park等[9]采用有限元分析軟件MARC研究了涂層鋼板與橡膠密封件間的球形磨粒對接觸特性的影響，揭示了任何微小磨粒的存在都可以導致非常大的接觸壓力和Mises應力，并造成嚴重磨損。但該文獻并未針對磨粒的大小、形狀等因素進行詳細討論。張峰等[10]針對含有表面缺陷的O形密封圈進行有限元分析，研究了錯模、分模扯縮以及分模飛邊等表面缺陷對密封性能的影響。不過，該文獻所研究的表面缺陷并非出現在密封界面，因而其有限元分析的結果均滿足密封條件，這對密封界面出現表面缺陷的情況并不適用。

本工作將在已有研究的基礎上，采用有限元方法深入研究金屬表面缺陷對硅橡膠密封性能的影響規律。首先，采用ABAQUS軟件建立含表面凸起的密封面接觸模型；然后，開展表面凸起對硅橡膠密封性能影響的研究，揭示表面凸起的高度（h）、半徑（r）、位置（l）對接觸壓力和接觸面積的影響規律，為密封件的設計和使用提供參考和依據。

1 有限元建模

1.1 表面缺陷形貌的表征

在加工或使用過程中，金屬表面容易產生表面凸起缺陷。表面凸起分為點狀缺陷和帶狀缺陷，兩種缺陷發生泄漏的原理相同，都是由于凸起周圍產生較低的接觸壓力區域造成。因此，本研究將兩種表面凸起缺陷都簡化為不同高度和半徑的球體來表示，如圖1所示。考慮到表面缺陷的位置對密封性能的重要影響，本文采用凸起與密封件對稱軸之間的距離來定義其位置，具體參數見表1。其中，高度和半徑為零表示無缺陷的理想表面。

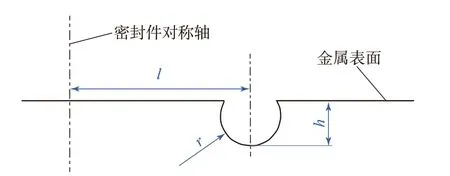
圖1 表面缺陷的三維形貌

表1 表面凸起參數

1.2 橡膠材料的本構模型

本工作研究的密封材料為航空航天常用的硅橡膠密封材料。基于拉伸壓縮試驗數據，采用超彈性本構模型Ogden（N=3）模型來描述其材料力學性能。Ogden應變能以3個主伸長率為變量，其應變能函數為[11-13]：

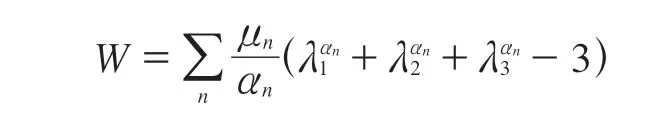
式中，nα可取任意值，μ n為待定系數。

一般情況下，為表示3種常見的應變模式（單軸拉伸、單軸壓縮以及純剪切），常取N=3，即n=1，2，3，對應的單軸拉伸與壓縮的應力應變關系如下：

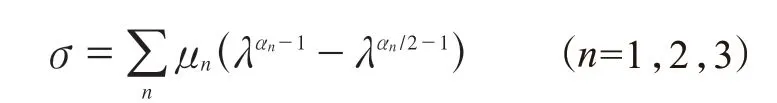
通過對硅橡膠密封材料進行單軸拉伸與壓縮試驗，將獲得的數據輸入ABAQUS軟件中進行擬合，得到本構模型的各項系數。Ogden模型各項系數的擬合結果為：1α2.828 41，1μ-105.335，2α3.719 39，2μ44.537 1，3α61.929 5，3μ1.922 05。

1.3 密封接觸的有限元模型

含表面缺陷的密封接觸有限元模型如圖2所示。假設密封件表面光滑，忽略硅橡膠材料的表面粗糙度；不考慮金屬的變形，將其簡化為剛體。硅橡膠網格單元類型選取CPS4R。橡膠與金屬之間的接觸使用Penalty模型，摩擦因數取0.225。固定密封件，利用位移加載方式，使金屬表面向下運動對密封件施加壓縮載荷，最大壓縮量設置為9 mm。

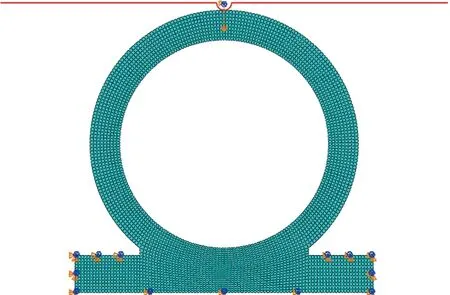
圖2 含表面缺陷的密封接觸有限元模型

2 結果與討論

2.1 接觸壓力對密封性能的影響

圖3示出了密封界面的接觸壓力分布。可以看出，對于理想的密封界面，隨著壓縮量的增大，最大接觸壓力的位置從中心向兩側過渡，呈對稱分布，有助于實現雙重密封的作用；而中心位置的接觸壓力為零。對于含表面缺陷的密封界面，最大接觸壓力出現在凸起位置，而凸起周圍的接觸壓力均為零，密封界面兩側存在較大的接觸壓力區域。事實上，不論是點狀凸起或者帶狀凸起，由于凸起周圍接觸壓力為零，凸起所產生的最大接觸壓力并不能實現有效密封，密封介質仍可通過凸起周圍的低接觸壓力區域發生泄漏。因此，密封界面兩側產生的接觸壓力區域為有效密封區域。本研究采用此區域的最大接觸壓力作為評價表面缺陷對密封性能影響的指標。

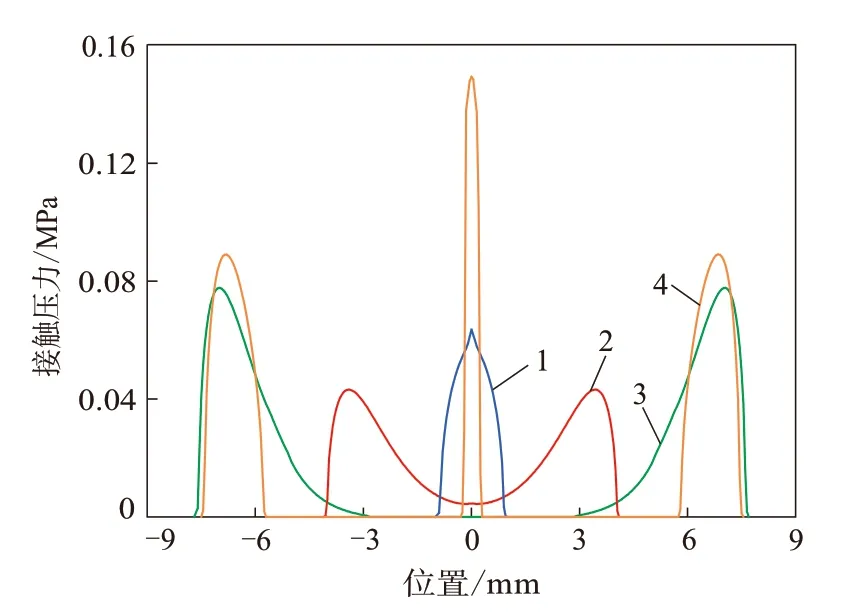
圖3 密封界面接觸壓力分布

2.2 表面凸起對密封性能的影響

2.2.1 凸起高度

圖4示出了表面凸起的高度對最大接觸壓力的影響規律。結果表明，對于理想密封界面，隨壓縮量的增大，最大接觸壓力并非單調增大，而是先增大后減小再增大。在壓縮初始階段，接觸壓力增長較快；隨著壓縮量的增大，由于接觸面積增長較快，使得接觸壓力不斷減小；在壓縮量大于3 mm時，接觸壓力由一個峰值分解為兩個對稱的峰值（見圖3），最大接觸壓力達到最低點；隨后，接觸壓力不斷增大。在密封件實際使用過程中，應盡量避免壓縮過程中接觸壓力出現較大波動，以保證密封的穩定性。因此，密封件工作時的壓縮量應大于3 mm，使接觸壓力處于單調上升的區間內。

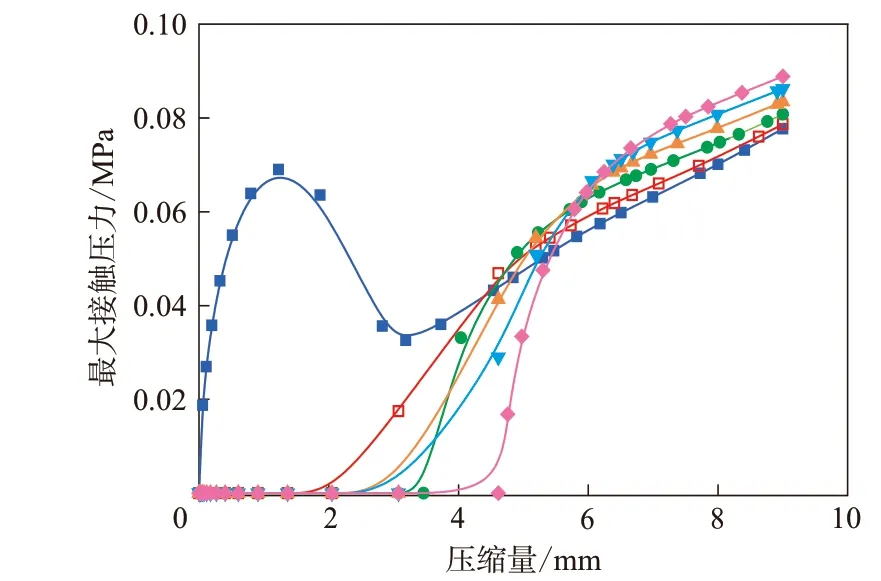
圖4 凸起高度對最大接觸壓力的影響

另一方面，表面凸起的產生有助于改善接觸壓力不穩定的現象，使最大接觸壓力呈現單調上升的趨勢。在壓縮前期，凸起的高度越大，達到相同的接觸壓力所需要的壓縮量越大，這是由于克服凸起的高度消耗了一部分壓縮量；在壓縮后期，當壓縮量為9 mm時，隨著凸起高度的增大，最大接觸壓力呈增大趨勢，說明當凸起高度在較小范圍時，有助于提高密封界面的接觸壓力。這是因為凸起的出現會減小接觸面積，當凸起高度較小時，接觸壓力的變化主要受接觸面積的影響。

圖5示出了表面凸起高度對接觸面積的影響規律。不難看出，對于理想密封界面，在壓縮前期，接觸面積隨著壓縮量的增大而增大，壓縮量為6 mm時達到最大值；當壓縮量大于6 mm時，密封界面中部出現間隙，接觸面積開始減小。由圖3也可以看出，當壓縮量達到9 mm時，密封界面中部的接觸壓力為零，說明此區域并未真正接觸。另一方面，表面缺陷對接觸面積的影響較大。在壓縮量為9 mm時，無缺陷的密封界面的接觸面積是有缺陷的2倍左右；隨著凸起高度的增大，接觸面積逐漸減小。

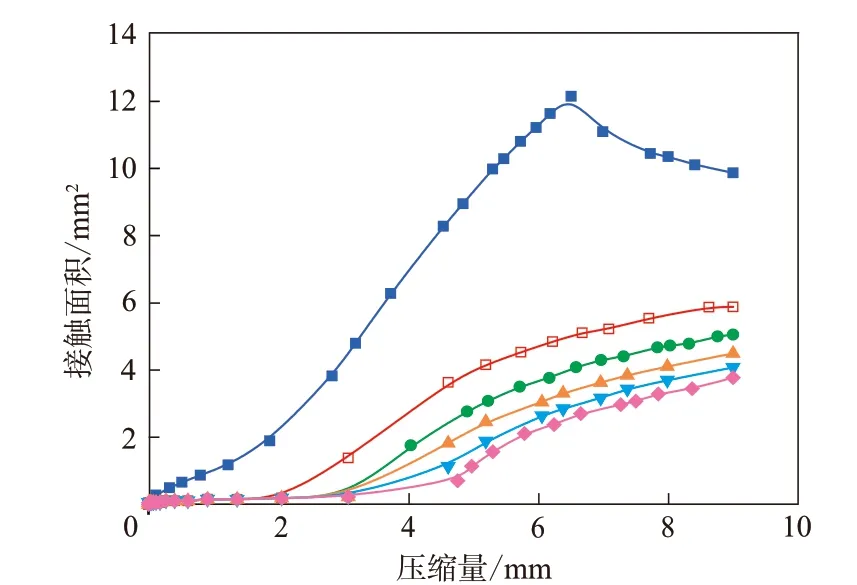
圖5 凸起高度對接觸面積的影響

2.2.2 凸起半徑

圖6示出了壓縮量為9 mm時表面凸起半徑對密封性能的影響規律。可以看出，當凸起缺陷存在時，最大接觸壓力增大了8%，接觸面積卻減小了55%，很難保證有效密封。另外，凸起的半徑越大，最大接觸壓力越大，接觸面積越小。但是，接觸壓力和接觸面積的變化幅度均很小，因而凸起半徑對密封性能幾乎沒有影響，可以忽略。

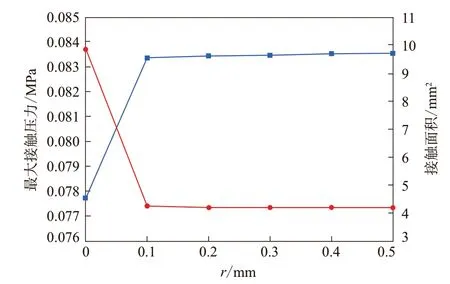
圖6 凸起半徑對密封性能的影響

2.2.3 凸起位置

圖7示出了表面凸起的位置對密封性能的影響規律，其中，原點為密封件對稱軸所處位置。從圖7可以看出，凸起出現的位置對密封性能的影響較大。當凸起靠近原點位置時，接觸壓力較大；隨著距離的增大，最大接觸壓力有增大趨勢；當凸起出現的位置為8 mm左右時，最大接觸壓力急劇減小。由圖3可知，理想密封界面的接觸壓力峰值出現在距離原點8 mm處左右。因此，當凸起位置距離接觸壓力峰值越近時，最大接觸壓力越小。另外，當凸起距離原點較近時（6 mm內），凸起的位置對接觸面積的影響較小；當凸起超過接觸壓力峰值的位置時，接觸面積急劇增大，但此時只能產生單側的接觸壓力峰值，無法實現雙重密封。

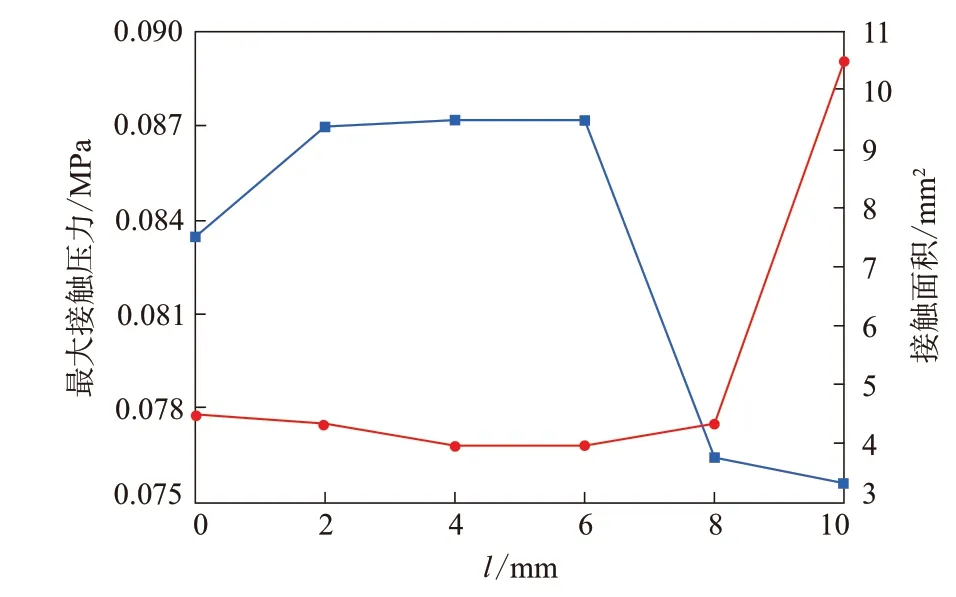
圖7 凸起位置對密封性能的影響

3 結論

本研究基于ABAQUS軟件，建立了含表面缺陷的密封接觸模型，重點分析了表面凸起的高度、半徑及位置對密封性能的影響規律，得到如下結論。

（1）在壓縮過程中，理想密封界面的接觸壓力會出現波動，不利于密封；接觸壓力呈對稱分布，最大接觸壓力出現在密封界面兩側。接觸面積隨壓縮量的增大呈現先增大后減小的趨勢；在壓縮后期，密封界面中部出現間隙。

（2）表面凸起缺陷對密封性能影響顯著。密封界面的最大接觸壓力出現在凸起位置，但此接觸壓力并不能保證有效密封，凸起兩側產生的接觸壓力區域為有效密封區域。凸起缺陷的產生能消除接觸壓力的波動現象，在一定程度上有助于提高密封界面的接觸壓力，但會使接觸面積急劇減小，導致泄漏。

（3）凸起的高度和位置對接觸壓力和接觸面積影響較大，凸起高度越大、距離接觸壓力的峰值位置越近時，越易發生泄漏；而凸起半徑對密封性能的影響相對較小。