分布式邊界層吸入推進系統的建模與分析

達興亞，范召林，熊能，吳軍強，趙忠良

中國空氣動力研究與發展中心 高速空氣動力研究所，綿陽 621000

隨著資源問題、環境問題、運營成本問題的日益突出，民用航空產業對飛機的節油降耗關注度越來越高。為了滿足未來的發展需求，美國從航空發動機技術、飛機布局技術等方面開展了大量前沿研究，力爭在2035年使飛機的燃油消耗降低60%[1-2]，這就是著名的N+3目標。但無論是優秀的翼身融合布局，還是高效率航空發動機，均難以實現這一苛刻的指標要求。為此，歐美國家開始從推進/機體一體化角度出發，研究新的技術手段，其中之一便是邊界層吸入技術。Ashcraft等[2]認為，邊界層吸入技術在N+3代飛機推進領域的關鍵技術中排第4位，相關性僅次于電機、先進燃燒技術和替代燃料。

邊界層吸入技術早在20世紀40年代就有研究[3]，但受限于發動機技術水平，一直沒有應用。20世紀90年代，Smith針對巡航導彈研究發現，邊界層吸入技術可降低7%的油耗[4]。20世紀末，斯坦福大學Rodriguez團隊研究了邊界層吸入技術在翼身融合體上的應用，并探索了邊界層吸入進氣道的二維和三維設計方法[5-6]。2003年，Daggett等分析了邊界層吸入式進氣道流動控制技術在翼身融合飛機上的應用[7]，他們將機體背部安裝的3個短艙進氣布局改為邊界層吸入布局后，發現可進一步降低油耗5.5%。Kawai等[8]針對該布局分析發現，使用主動流動控制技術能使油耗下降達到10%。

麻省理工學院針對邊界層吸入技術也開展了大量研究，包括Freuler開展的“Silent Aircraft”(靜音飛機)邊界層吸入式進氣道設計[9]、Plas等開展的系統建模分析[10-11]。“Silent Aircraft”與Daggett和Kawai等研究的布局類似。Plas等[11]從飛機的尾跡和推進功率角度分析了邊界層吸入的影響。發動機對氣流做功是阻力與噴流速度之積的線性函數，在吸入尾跡的情況下則是阻力與尾跡速度之積的線性函數，因此，吸入尾跡會使功率降低，從而達到省油的目的。Plas等的建模結果表明邊界層吸入能夠帶來3%～4%的燃油經濟性[10-11]。這只是推進系統的效益，并不包含機身氣動特性改善的貢獻。

更加超前的設計是吸入機體全部或大部分邊界層。2009年，NASA的Felder等提出了應用邊界層吸入技術的N3-X飛機[12]。該飛機使用了分布式電推進技術，利用渦輪發電機驅動飛機背部的一排分布式推進風扇，進而全部吸入機體背部的邊界層。Felder等只給出了推進系統的設計參數，并未給出設計方法和參數選擇依據。美國通用電氣公司提出了管狀飛機邊界層吸入技術[13]。該方案在傳統飛機的管狀機身尾部安裝一個額外的電推進風扇，用來吸入全部機體邊界層并提供部分推力，計算表明該方案可降低2個單位的機身阻力，并增大3個單位的推力[14]。可見，大范圍的后體邊界層吸入技術不僅能直接降低推進系統的功率需求，還能改善機體的氣動特性。

國內對邊界層吸入技術的研究主要集中在外流，閆萬方等[15]分析了分布式推進關鍵參數對全機氣動特性的影響，研究構型與N3-X類似，主要參數是推進系統流量、安裝位置和高度。項洋等[16]分析了邊界層吸入對翼型氣動特性的影響。上述工作均不涉及燃油消耗分析。寧樂等[17]從進氣道內流角度分析了邊界層吸入對S彎進氣道性能的影響，主要參數是整流罩的最大厚度和位置、進氣位置和進口高度。

以上研究工作基本明確了邊界層吸入式推進技術的應用前景，但是還沒有研究推進系統的參數化影響，不明確關鍵參數的影響規律，仍未建立起推進系統的設計方法。本文面向邊界層吸入式推進系統的設計與應用，開展詳細的推進系統參數化影響分析，進而獲得關鍵參數的影響規律，為推進系統設計提供數據支撐。

1 研究對象

本文研究對象是類似于N3-X的渦電分布式推進系統。圖1為N3-X翼身融合飛機布局[12]。推進系統安裝在飛機背部，進氣道要吸入機體邊界層。在N3-X的翼尖，布置了兩個發電用的渦輪發電機。這種布局具有如下優點：① 依靠邊界層吸入，提高推進效率，降低風扇驅動功率；② 推進系統與機身融合設計，改善尾部氣動性能；③ 依靠機身遮擋，降低噴流和風扇噪聲；④ 通過風扇動力差產生矢量推力；⑤ 能夠容忍單個或多個風扇故障；⑥ 機翼兩側的發動機有降低誘導阻力的效果。N3-X共設計了14個電推進風扇，直徑為1.285 m，壓比為1.35。

圖1 N3-X翼身融合飛機布局[12]Fig.1 Blended wing-body configuration of N3-X[12]

2 推力模型

2.1 內推力公式

對于翼吊發動機，常常把控制體的邊界取在前無窮遠至后無窮遠，得到的是非安裝推力，也是發動機臺架試驗得到的推力。非安裝推力表達式為

(1)

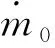
本文利用圖2中的外流控制體和內流控制體，結合動量公式，可首先推導出式(1)中的非安裝推力公式，然后結合自由流管控制體，可推導出機體推阻力平衡公式(也就是內推力公式)。利用動量方程推導推力公式的過程較為簡單，但比較冗長，這里只給出結果，具體思路可參考文獻[19]。機身阻力滿足：

(2)

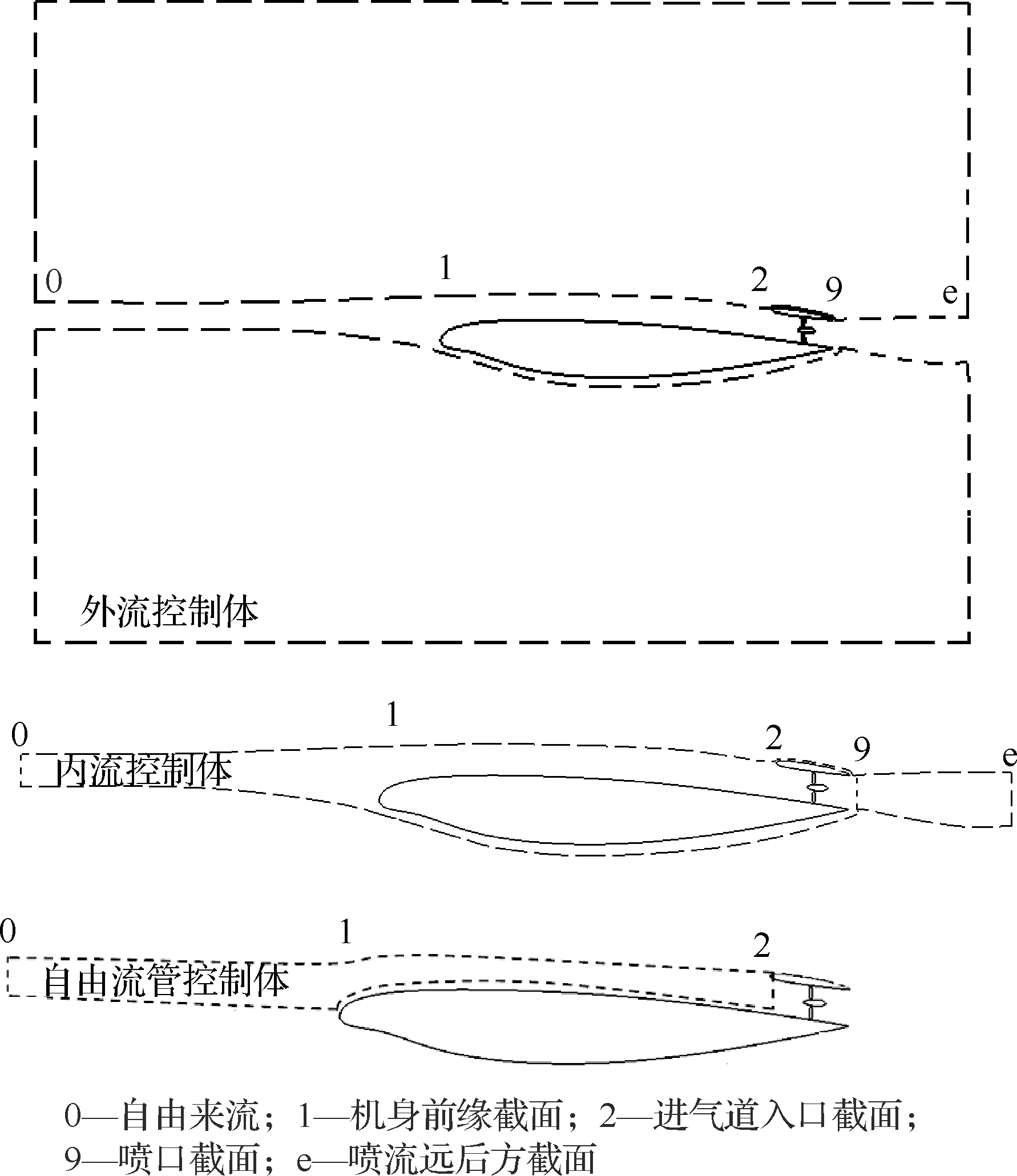
圖2 控制體示意圖Fig.2 Sketch of control volumes

式中：Dbody為機體阻力；下標“2”代表進氣道入口截面。機體阻力包括吸入阻力、外罩阻力和未吸入的機體阻力。因此，本文把推力劃分為進氣道入口至噴管出口截面。由于機身阻力應與內推力相等，式(2)也即內推力公式。

2.2 邊界層修正

在吸入邊界層情況下，將推力公式調整為

(3)

式中：Teff為內推力，即有效推力(下文簡稱推力)；θ為邊界層的動量厚度；ρ為密度;下標“t”、“b”、“E”分別代表上表面、下表面和邊界層邊緣。假設邊界層邊緣速度與核心流速度相等，那么有

(4)

3 推力計算方法

3.1 計算方法

由于推進系統寬度較大，可將其簡化為二維系統。建立如圖3所示的計算域，入口為進氣道入口截面，出口為噴管出口截面，上邊界為進氣道和噴管的上物面，下邊界為機體物面。采用積分邊界層方程組求解邊界層在計算域內的發展，再代入到式(4)中即可求解出推力。

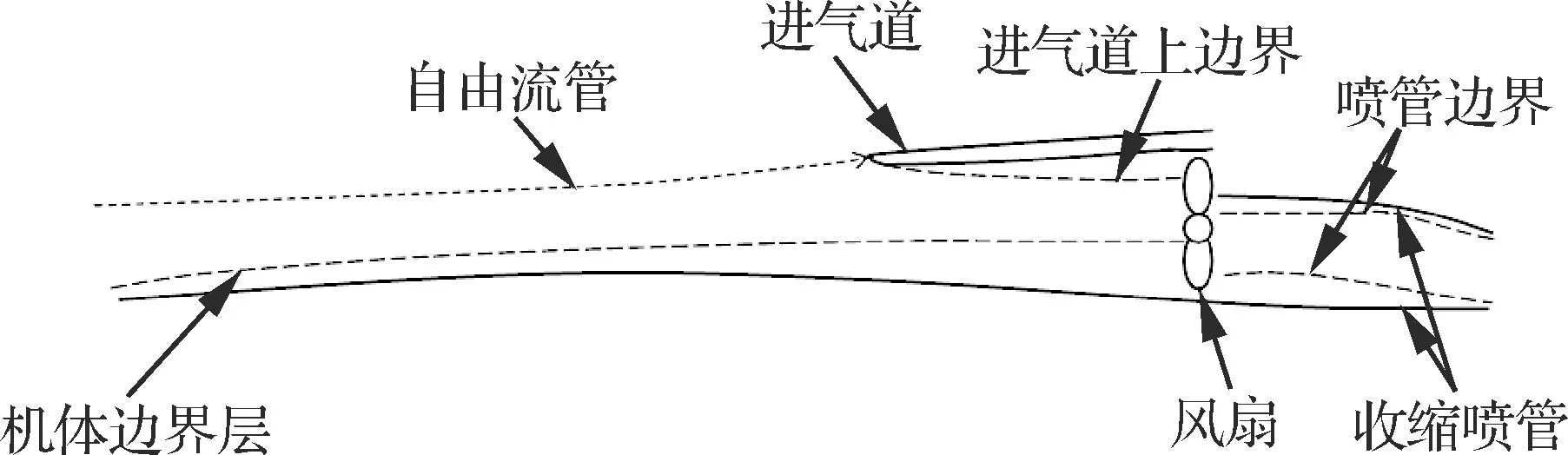
圖3 二維計算域Fig.3 Two-dimensional computation zone

3.2 控制方程

假設整個計算域內風扇前后的總溫保持不變，核心流速度與邊界層邊界速度相等，那么對于進氣道和噴管邊界層，控制方程組為

式中：δ*為位移厚度；Cf為摩擦阻力系數；CD為擴散系數；其余量的定義和計算公式參照文獻[20]。式(5a)和式(5c)為上下壁面邊界層的動量方程，式(5b)和式(5d)為上下壁面邊界層的能量方程,式(5e)為整個通道的連續方程。

3.3 方程組求解

積分邊界層公式的好處是在已知x=xk坐標點的uE、δ*、θ的情況下，通過求解邊界層積分方程組就可以獲得下一坐標點x=xk+1的uE、δ*、θ。積分邊界層方程是一組高度非線性的常微分方程組，其求解依賴于數值方法。對于微分項，一律按照中心差分格式構建:

(6)

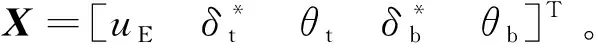
R(Xk,Xk+1)=0

(7)

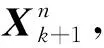
(8)

其中：

(9)

這樣，不斷更新Xk+1直至殘差R縮小到可忽略的水平。

積分邊界層方程的求解還需要知道面積變化律。進氣道和噴管的面積采用經典的三次多項式構建，其表達式為

A=ΔA[3(x/L)2-2(x/L)3]

(10)

式中：ΔA為面積變化量；L為長度。

3.4 邊界層速度分布

在得到邊緣速度、動量厚度、位移厚度后，采用Swafford邊界層模型估算邊界層速度分布，進而通過插值求得邊界層厚度。Swafford邊界層模型求解方法為[21]

(11)

(12)

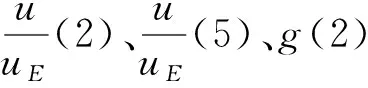
另外，也可采用Coles邊界層分布公式[10]。Coles分布的優點是可直觀地得到邊界層厚度δ隨形狀因子H和動量厚度θ的變化規律：

(13)

邊界層厚度δ與形狀因子H呈非線性關系，但隨動量厚度θ近似呈線性變化。Swafford分布得到的邊界層厚度與Coles分布會有一定差異，但隨H和θ的變化規律是相似的。Coles分布對近壁面速度作了簡化，Swafford分布要更合理一些，因此本文采用Swafford邊界層分布。

3.5 風扇模型

風扇對上游流動具有抽吸效應，總的效果是使邊界層變得更薄，速度剖面更均勻。經過風扇后，邊界層流態也會發生變化，風扇壓比越大，這種上、下游影響也就越明顯。準確評估風扇對進氣道邊界層影響的難度較大，但是考慮到分布式電推進通常使用低壓比風扇，上游影響較弱，對畸變的改善作用也較小。因此本文忽略風扇對上游邊界層的影響。畸變對風扇的影響主要通過壓比π和效率η下降來體現。對于低壓比風扇，優秀的氣動設計可確保效率下降在0.5%左右[22]，而平均壓比有可能增大(小流量時壓比更高)。根據進氣道出口的流量平均總壓和風扇壓比，可以估算出風扇出口平均總壓。根據進氣道出口總溫(假設恒值)和風扇效率、壓比可以估算出風扇出口總溫。根據流量守恒可以估算出風扇出口的主流速度。

4 推進系統總體性能分析

4.1 基準狀態及與N3-X的對比

基準狀態的選取參照N3-X，目的是驗證計算模型和方法，并以此為基礎開展參數化分析。

飛行高度為104m，飛行馬赫數為0.8。具體參數為：進氣道入口高度為1.2 m、擴張比ER為1.2、長徑比為2；噴管長徑比為2、出口面積根據出口馬赫數為0.9確定，進氣道入口馬赫數為0.7；假設風扇壓比π為1.35、效率η為92%，風扇效率損失1%；邊界層狀態取形狀因子H為1.6、動量厚度θ為0.1 m。定義吸入邊界層占比為邊界層厚度與進氣道入口高度的比值，那么此狀態下吸入邊界層占比為56%。

引入功推比，其定義為單位寬度推進系統驅動風扇所需功率與內推力的比值，單位為W/(N·m)。風扇所需功率為

(14)

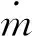
根據文獻[12]中給出的推進系數數據，N3-X在巡航狀態的設計結果是：進氣道高度為0.785 m、入口馬赫數為0.8、單臺風扇流量為108 kg/s、風扇壓比為1.35、效率為92%、推力為8 864 N、電機功率為2.77 MW，吸入邊界層占比為58.3%，不確定NASA設計時是否考慮風扇損失，但從文中的數據可以看出Felder等采用的是一維和二維的綜合設計方法：假定一個入口邊界層分布，粗略估算進氣道的阻力和總壓損失。根據流量可計算出單臺風扇對應的進氣道入口寬度為1.39 m，因而功推比為 224.8 W/(N·m)。

本文選取的基準狀態僅進氣道入口高度不一致，但是邊界層的相對厚度接近，風扇的壓比和效率也相同，得到的功推比接近，一定程度上說明了本文結果的可信性。

4.2 邊界層狀態的影響

圖4為不同進氣道邊界層狀態下，單位寬度推進系統產生的推力和功推比圖。3組扇形區域分別對應不同的風扇損失，從上往下依次為2%、1%、無損失。從扇形上頂點向外共5條曲線，動量厚度θ從0 m依次遞增到0.10 m，順時針方向共5條曲線，形狀因子H從1.60遞增到2.60。根據Swafford邊界層分布公式，在H=1.60時邊界層厚度最大達到入口高度的56%，在H=2.60時邊界層厚度最大達到入口高度的53%，對應Coles公式的值分別為53.3%、52.8%，兩者相差不大。

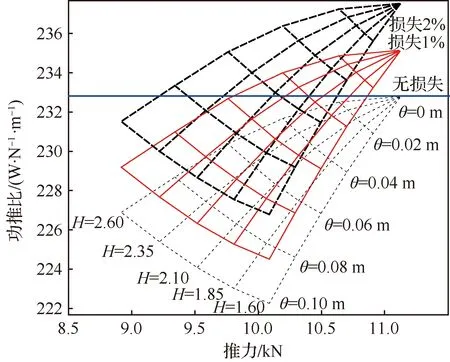
圖4 邊界層狀態對推力和功率的影響Fig.4 Effect of boundary layer on thrust and power

從圖4中可以看出來，在進氣道入口高度、馬赫數和擴張比一定的情況下：

1)形狀因子一定的情況下，隨著動量厚度的增大，推進系統產生的推力減小，但是功推比降低。這是因為，形狀因子一定，動量厚度越大，位移厚度也就越大，邊界層厚度也增大，相當于增大了吸入的邊界層占比。由于位移厚度增大，入口的流量降低，進而導致推力減小，但由于功率下降更明顯，所以功推比呈下降變化。風扇推力減小意味著需要更寬的推進系統，從而可以吸入更多的機體邊界層，有利于改善飛機氣動特性[12,15]。

2)動量厚度一定的情況下，隨著形狀因子的減小，推擠系統產生的推力增大，并且功推比降低。這是因為，動量厚度一定，形狀因子從2.60降到1.60，邊界層的厚度變化較小(根據式(13))，而位移厚度明顯降低。此時入口速度分布更加飽滿，入口流量增大，進而導致推力增大，但由于功率增量要小于推力增量，所以功推比下降。

3)壓比不變的情況下，風扇的效率損失越大，功推比近似等比例增大。由于推力主要受壓比影響，所以基本保持不變。

圖4中零損失對應的扇區頂點代表無吸入邊界層情況，其功推比為232.7 W/(N·m)。如果要發揮出邊界層吸入帶來的好處，功推比應小于這一數值。從圖中可以看出，當風扇損失為1%、H=1.60、θ=0.10 m時，可節省約3.52%的燃油消耗；當風扇損失為2%、H=1.60、θ=0.10 m時，可節省約2.54%的燃油消耗。目前，美國設計的畸變容忍風扇在邊界層吸入情況下風扇效率損失為0.5%[22]，按H=1.6、θ=0.10 m計算可節省約4%的燃油消耗，這對民用航空產業的影響是不可估量的。對于1%損失扇區，大部分狀態下均能降低燃油消耗，而對于2%損失扇區，大部分狀態下燃油消耗都有所增大。因此，畸變容忍風扇是邊界層吸入式推進技術的關鍵。

4.3 進氣道入口馬赫數和擴張比的影響

進氣道入口邊界層取H=1.60、θ=0.10 m進行分析，風扇、噴管的參數與4.1節相同，風扇效率損失取1%，入口馬赫數從0.65變化到0.80，擴張比ER從1.20變化到1.40。

圖5給出了擴張比和入口馬赫數對出口馬赫數的影響。分析范圍內，進氣道出口馬赫數保持在0.52～0.66之間，是典型的進氣道出口馬赫數。等入口馬赫數下，隨著擴張比的增大，出口馬赫數下降，而等擴張比下，出口馬赫數隨入口馬赫數基本呈線性變化。

表1給出了進氣道擴張比對功推比的影響。相同擴張比下，進氣道入口馬赫數對功推比具有比較大的影響，入口馬赫數越大，功推比越小。相同入口馬赫數下，進氣道擴張比對功推比的影響不明顯，擴張比越大，進氣道產生的總壓損失也會略微增大，從而會帶來一定損失。在設計時，擴張比的選擇要兼顧進氣道出口速度，并確保不發生流動分離。改變入口馬赫數相當于改變入口流量，此時來流總壓和總溫不變，這與改變飛行馬赫數是不同的。

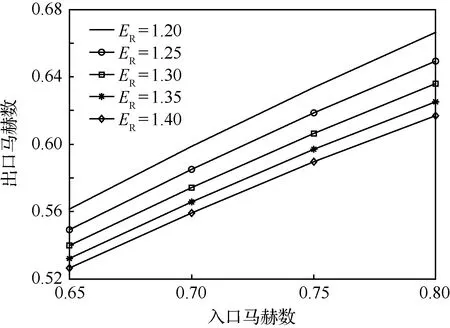
圖5 擴張比和入口馬赫數對出口馬赫數的影響Fig.5 Effect of expanding ratio and inlet Mach number on outlet Mach number

入口馬赫數功推比/(W·N-1·m-1)ER=1.20ER=1.25ER=1.30ER=1.35ER=1.400.65245.0245.1245.2245.3245.40.70225.2225.3225.4225.4225.60.75209.1209.3209.4209.6209.70.80195.6195.8196.0196.1196.3

4.4 風扇工作特性的影響

風扇效率損失取1%，入口邊界層取H=1.60、θ=0.10 m進行分析。圖6為風扇工作特性對油耗的影響，其中網格線上風扇出口的H值均為1.60。可以看出，推力和功推比均隨著壓比的增大而增大，表明增大壓比會導致油耗增加；相同壓比下，效率越高功推比越低，同時效率對推力影響要弱一些。總的來看，壓比對功推比的影響要大于效率，例如，對于出口形狀因子H=1.60曲線，壓比為1.25、效率為0.92時，功推比僅為211.7 W/(N·m)，而壓比為1.35、效率為0.92時，功推比為225.4 W/(N·m)，增幅達到了6.5%。圖6表明，如果提高推進風扇效率的難度較大，可以在壓比和效率之間進行權衡，選擇低壓比風扇。不足的是，低壓比風扇產生的推力較小，應用中需要折衷考慮飛機后體形狀，確保有足夠的空間裝載一排低壓比風扇。

風扇具有減弱畸變的作用，出口的邊界層會變得更為飽滿，進而改變動量厚度和形狀因子。圖6中的圓點代表了噴管入口(即風扇出口)邊界層形狀因子的影響。此時相對動量厚度與進氣道出口保持不變，而風扇壓比均為1.35，形狀因子由上至下等差地從1.20變到1.60時，功推比從240.8 W/(N·m)降低到225.4 W/(N·m)。這是因為，隨著形狀因子增大，邊界層變得更薄，核心流速度降低，從而使噴管的動量損失減小。由于噴管入口邊界層變化并未影響風扇的工作狀態，風扇的驅動功率不變，所以功推比降低。本文同樣分析了邊界層動量厚度影響，當噴管入口邊界層的相對動量厚度減小后，其功推比如圖6星形點所示，其中形狀因子依然是由上到下等差地從1.20變到1.60。這說明噴管入口邊界層狀態的改變具有增大或減小功耗的雙重功能，總體上是功推比隨形狀因子增大而減小，隨邊界層動量厚度減小而減小。對于小壓比風扇，它對進氣畸變的削弱作用不會太強，推力和功率變化不會太大。

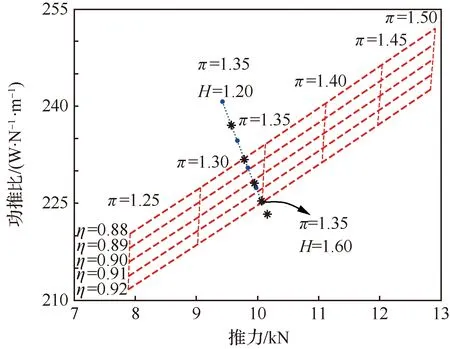
圖6 風扇壓比和效率對推力和功率的影響Fig.6 Effect of fan pressure ratio and efficiency on thrust and power

4.5 噴流速度的影響

表2給出了噴流速度對功推比的影響，其中風扇壓比取1.35、效率取0.92，邊界層狀態按H=1.60、θ=0.10 m給定。從表中可以看出來噴管的噴流速度越大，產生的推力越小，這是因為要達到更高噴流速度，必須增大噴管的收縮比，致使噴管阻力增大，此時由于風扇的工作狀態并未改變，所以導致總的推力降低。如果用式(4)進行解釋，推力減小的原因則在于噴管出口面積減小、靜壓減小。

上述分析忽略了外流對亞聲速噴管的影響。當噴管出口達到聲速，才能確保外流對推進系統內流的影響降到最低。如果噴流和外流之間沒有產生不利干擾，可考慮降低噴流速度。一般來說，噴流速度必須大于飛行速度，對應本文則是239 m/s。

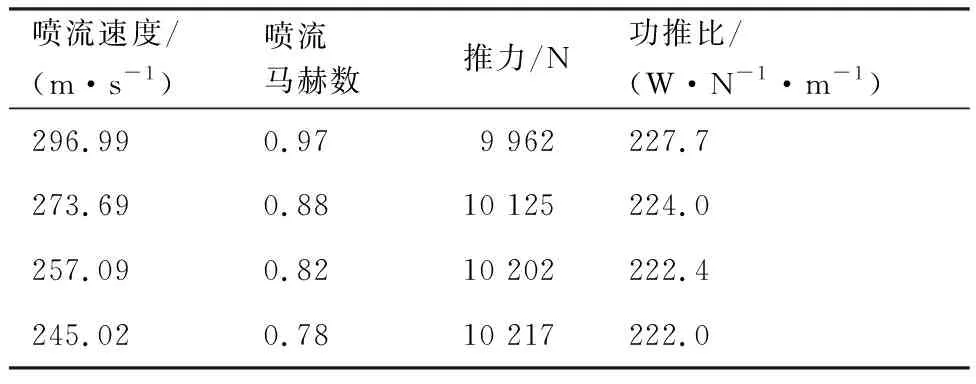
表2 噴流速度對功推比的影響Table 2 Effect of jet velocity on power-thrust ratio

4.6 其他參數的影響

其他參數還包括進氣道入口高度和長徑比。進氣道入口高度實際影響吸入邊界層占比，與圖4改變邊界層狀態的結果是一致的。進氣道和噴管長徑比主要影響摩擦阻力，長度越大，摩擦阻力越大，流道損失也就越大，但本文計算結果表明它們對推進系統總體影響均不大。

5 結 論

1) 基于積分邊界層方程組的計算方法，能夠獲得與N3-X十分接近的功推比預測結果，說明該方法是合理可信的。

2) 邊界層狀態(動量厚度和形狀因子)對推進系統能耗的影響呈扇形網狀分布，原點對應無邊界層吸入情況，隨著動量厚度增大或者形狀因子減小，推進系統的能耗降低。

3) 根據風扇效率損失情況，在不計及飛機阻力降低的情況下，吸入邊界層占比50%左右時可節省4%的能量消耗。

4) 進氣道擴張比對推進系統能耗的影響比較小，而進氣道入口馬赫數對能耗影響較大。

5) 風扇效率對推力幾乎無影響，對功推比的影響也要弱于風扇壓比。

6) 風扇對畸變的改善效應具有增大或減小功耗的雙重功能，風扇后形狀因子變大或者邊界層位移厚度變小，功推比都將變小。

7) 噴流速度越低，功耗越小，但要確保不會明顯增加噴流干擾阻力。