雙端柔直輸電系統的改進無差拍控制策略研究

張汀荃， 張汀薈， 張海龍，顧佳易

( 1. 南京師范大學南瑞電氣與自動化學院, 江蘇 南京 210042;2. 南京工程學院電力工程學院, 江蘇 南京 211167)

0 引言

隨著環境污染的日益加重，風能、太陽能等分布式能源以環保、可再生、運行靈活等優點成為研究的熱點，然而其缺點也非常突出，比如存在間歇性功率波動、遠離用電中心、規模小比較分散。另外，我國人口在不斷增長，城市用電量在不斷上升，城區供電網絡的改造擴容也變得日益重要[1-2]。柔性直流輸電技術(voltage source converter-high voltage direct current, VSC-HVDC)的出現很好地解決了上述難題。VSC-HVDC被大規模運用于實際工程，主要由電壓源型換流器(voltage source converter, VSC)、PWM調制技術等為基礎組成，在分布式能源并網、無源網絡供電和城區供電改造等場合擁有不可替代的優勢[3-5]。

本文以兩端柔直輸電系統為研究對象，建立兩端柔直數學模型，研究系統基本運行方式以及VSC控制策略。考慮傳統無差拍控制運用于VSC換流器時具有控制延時以及電流閉環控制響應性差等問題，因此提出一種改進無差拍控制策略，通過預測k+2時刻采樣電流，解決上述缺陷。最后通過聯合仿真，驗證所提方法的正確性與可靠性。

1 兩端柔直數學模型

如圖1所示，兩端柔直由換流站1、直流側電容、換流站2依次連接構成，直流側電容為系統提供穩定直流電壓，保證有功、無功潮流流動，電抗器XLi用以濾除整流端和逆變端輸入、輸出電流諧波。本文對系統進行分析時，為便于數學模型推導，忽略換流器并聯損耗，換流器串聯及其他損耗用等效電阻Ri表示[12-16]。

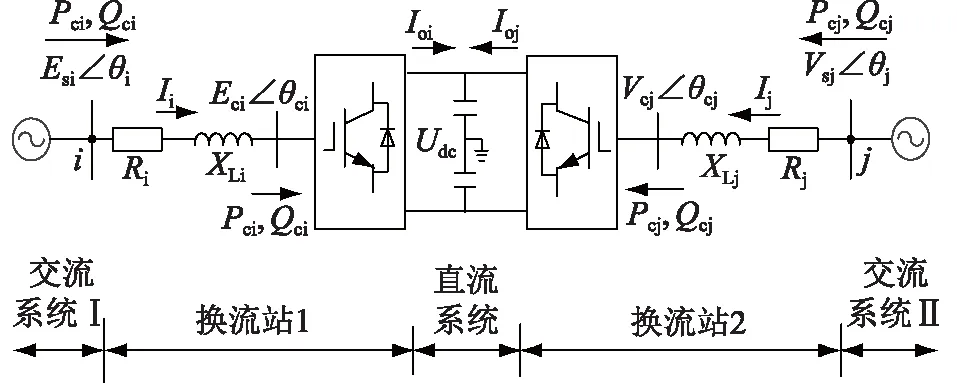
圖1 兩端柔直主電路結構Fig.1 VSC-HVDC main circuit structure

1.1 三相坐標系下兩端柔直數學模型

根據圖1，對柔性背靠背直流輸電系統列KCL方程，可得其在三相靜止坐標系下的動態微分方程：

(1)

式中：ij1，ij2分別為交流系統輸入、輸出電流；Esj，Vsj分別為交流系統輸入、輸出電壓；Ej，Vj分別為換流器1、換流器2交流側輸入、輸出電壓。

由于換流器1和換流器2結構參數對稱，故只對換流器1三相橋臂開關函數進行定義：

(2)

將式(2)代入式(1)得：

當今時代，計算機軟件發展的主流趨勢就是智能化，實現計算機軟件的智能化有助于對計算機的進一步應用和開發。人工智能技術在各個領域的應用越來越成熟，也越來越廣泛，對于相關計算機產品的需求也越來越智能化，這就使得計算機軟件相關開發過程在未來也會朝著智能化的方向發展，這也是未來軟件開發相關人員的工作重點和課題攻關的方向。

(3)

圖1可得直流側電壓方程為：

(4)

式中：udc為直流側電壓；i01，i02為直流側輸入或輸出電流。假設忽略換流器開關損耗，可得：

(5)

式中：Pc1，Pc2分別為換流器1、換流器2交流輸出或輸入有功功率。當直流側udc保持恒定時，系統處于穩定運行狀態，i01=i02，則Pc1=Pc2，即流入功率等于流出功率。可得結論：要實現柔性背靠背兩側功率的平衡，需保證直流側電壓的穩定。

式(3)構成了兩端柔直系統數學模型，式(4)構成了直流側電壓的數學模型，式(3)與式(4)構成兩端柔直系統在三相靜止坐標系下的數學模型。

由于三相靜止坐標系下參數均為變交流量，不利于系統控制與設計，所以需將兩端柔直數學模型轉化到同步旋轉的dq坐標系下，將三相靜止坐標系下的正弦變量轉化為同步坐標下的直流量。

1.2 dq坐標系下兩端柔直數學模型

根據式(3)、(4)建立兩端柔直在dq同步旋轉坐標系下的數學模型：

(6)

(7)

直流側電壓在dq旋轉坐標下的方程為：

(8)

式中：ω1，ω2為交流系統相電壓的角頻率；id1，id2，iq1，iq2為交流系統三相交流電流在dq軸上的分量；Esd，Vsd為兩端交流系統三相電壓在d軸上的分量；md1，md2，mq1，mq2為換流器開關函數在dq軸上的分量。式(6—8)共同構成兩端柔直系統在dq旋轉坐標系下的數學模型。

2 基于改進無差拍系統運行分析

2.1 傳統無差拍控制策略

無差拍控制綜合了系統狀態方程、系統輸出反饋方程以及所要求的下一時刻參考輸出方程最終計算出系統所需的開關脈沖。與其他VSC控制策略相比，具有開關頻率固定、動態響應快和高帶寬特性等優點，在實際中得到了廣泛的應用[17]。

在數字系統中，為實現無差拍的控制效果，需將系統下一時刻參考輸出量表示為系統狀態變量與輸出反饋變量之間的相互關系。根據式(6)、(7)，由于αβ軸上方程對稱，僅以α軸為例，可得α軸無差拍控制框圖，見圖2。圖中Gpwm(z)是PWM調制環節傳遞函數，Gp(z)是被控對象傳遞函數。

圖2 α軸無差拍電流控制框圖Fig.2 Block diagram of current loop with deadbead control

由圖2可知，傳統無差拍電流控制實際上已經成為了差一拍控制，無法實現無靜差跟蹤。且受限于系統硬件及控制器容量，系統采樣率不能過高。同時考慮系統運用環境，需要更高的控制精度及響應速率。因此，傳統無差拍控制已不能滿足實際工程應用要求，需進行改進，提高控制效果[18]。

2.2 改進無差拍控制策略

由于實際控制器存在采樣率、計算能力等限制，傳統無差拍無法實現采樣、計算、占空比輸出在同一時刻完成，總會存在采樣點超前占空比輸出點的情況。圖3是控制延時示意圖，圖中在第k時刻開始，系統仍執行的是k-1時刻PWM占空比Dk-1，而上一時刻的占空比Dk延時td才輸出。為進一步提高無差拍控制精度，修正由以上原因造成的周期性偏差，改進算法通過預測第k+2時刻的電流，這樣PWM占空比Dk+1可以在第k+1時刻提前執行，實現電流無靜差跟蹤。由于αβ軸上方程是對稱的，僅以α軸為例，可得α軸改進無差拍控制框圖，如圖4所示，其中S為補償器，用于被控對象相位補償。

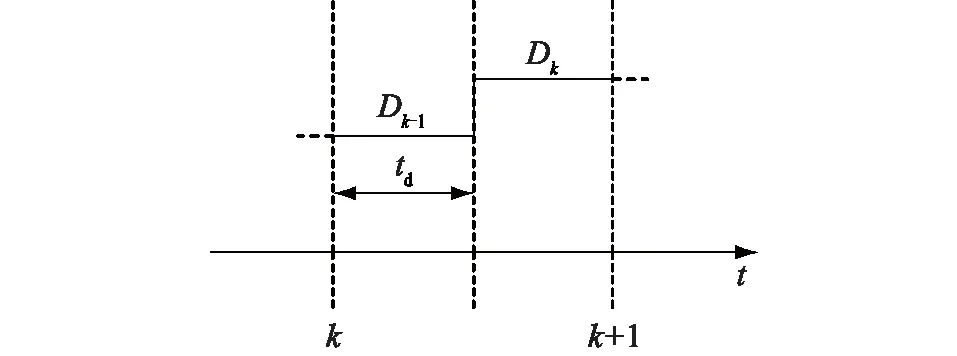
圖3 控制延時示意圖Fig.3 Sketch map of control delay

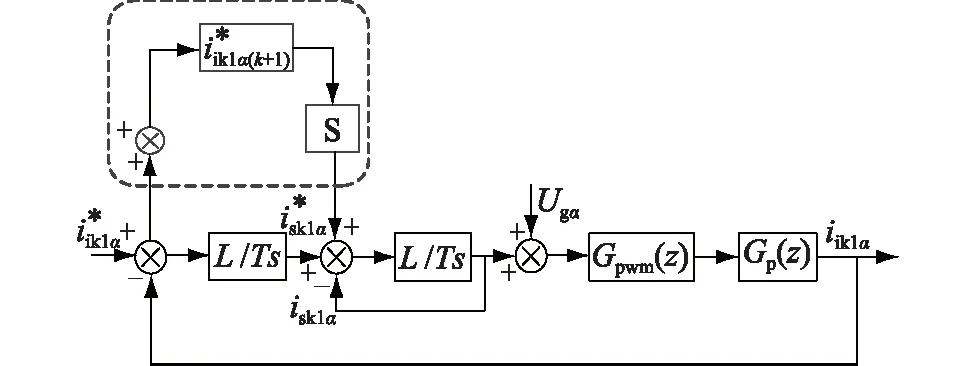
圖4 α軸改進無差拍控制框圖Fig.4 Block diagram of current loop with improvement deadbead control

由式(6)、(7)推算下一時刻電流值，忽略系統電容的影響，默認電流iik1=isk1=i，則第k+2時刻的α軸電流采樣值為：

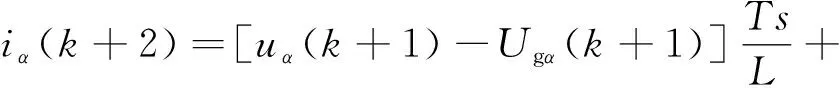
(9)

根據式(6)、(7)及式(9)可得第k時刻和第k+1時刻α軸的電流偏差值：

(10)

(11)

令第k+1時刻α軸的電流誤差等價于2個相鄰時刻電流誤差的平均值，表達式為：

(12)

將式(12)代入式(11)，可得系統交流側輸出電壓表達式：

(13)

相對于電網基頻而言，如果采樣周期較小，可以認為在α軸上網側電壓在連續3個采樣時刻采樣偏差相等，表達式為：

Ugα(k+1)-Ugα(k)=Ugα(k)-Ugα(k-1)

(14)

由式(14)可知，在第k+1時刻的電網電壓平均值可由前幾個采樣值的線性外推得到，表達式為：

Ugα(k+1)=Ugα(k)+[Ugα(k+1)-Ugα(k)]=
2Ugα(k)-Ugα(k-1)

(15)

假如網側電壓在連續4個采樣時刻采樣間隔也相等，即：

Ugα(k+2)-Ugα(k+1)=Ugα(k+1)-Ugα(k)=
Ugα(k)-Ugα(k-1)

(16)

由式(15)、(16)可得第k+1時刻網側電壓為：

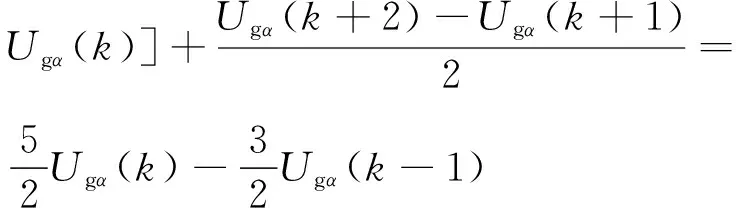
(17)

式(13)中第k+2時刻采樣電流為k采樣時刻的給定值，表達式為：

iα(k+2)=i*

(18)

根據以上分析，利用式(15)、(17)和式(18)可得Ugα(k+1)和iα(k+2)，將以上兩個結果代入式(13)，得到第k+1時刻兩端柔直系統交流測輸出電壓uα(k+1)，最后通過計算uα(k+1)與逆變器高壓側電壓Udc的比值，得到逆變器所需的PWM占空比Dk+1。

本節所提改進無差拍控制策略優點在于：(1) 式(13)與式(6)、(7)相比，電流不會突變，同時電流偏差減少1/2，有限改善電流波形質量；(2) 無需計算k+2電流，將k時刻電流值與k+1時刻電流值直接關聯；(3) 改善系統輸出電流波形，減少電流總諧波失真(total harmonic distortion，THD)[19]。但改進算法默認連續采樣時間間隔一致，因此一般適用于穩態環境，對于暫態環境還有待于進一步改善。

3 仿真驗證及分析

為驗證上文所提方法，搭建仿真系統，檢驗上述所提算法的正確性與有效性。系統主電路參數選取可參考文獻[20]，其中各器件具體參數如表1所示。

表1 系統主電路參數Tab.1 Parameters of main circuit system

3.1 仿真平臺構建

本節所采用聯合仿真平臺將由NI Labview 2014 sp1與Starsim軟件共同構成。其工作原理如下，Labview 2014 sp1負責數據采集、改進無差拍控制策略、兩端并網控制器、向無源網絡供電控制器等程序的編寫；Starsim負責搭建背靠背柔性直流輸電系統主電路包括2個電壓源型換流器、2個變壓器、2個電感以及2個交流配電網。在上位機中，通過桌面執行節點控件以及Starsim Design調用仿真程序、系統主電路，最終形成一個完整的仿真平臺。

3.2 仿真結果分析

如圖5所示，采用傳統VSC三角波控制策略，利用NI控制器中高斯白噪聲模塊，在指令電流中加入指定諧波信號以模擬復雜的電網環境，在采用上述策略時，可以看出網側電流發生明顯畸變,圖6利用快速傅里葉變換對此時網側電流分析，圖中3至7次諧波含量明顯高于其余各次諧波之和，系統產生大量諧波，嚴重危害配電網運行。

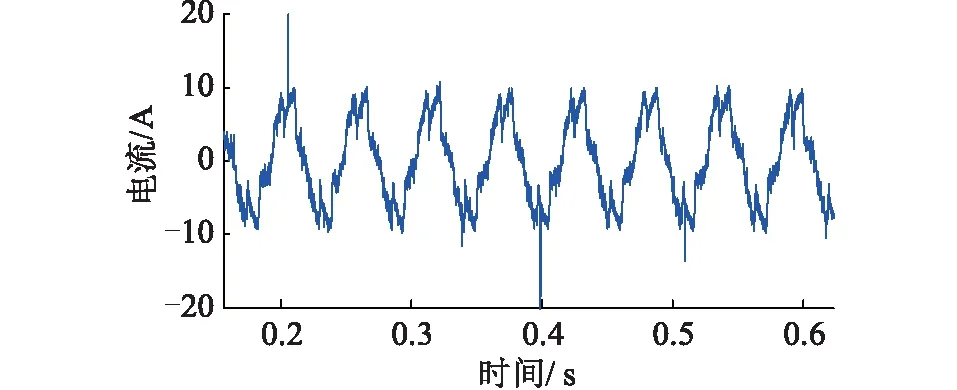
圖5 采用三角波控制時網側電流波形Fig.5 The grid side current waveform of untaken measures

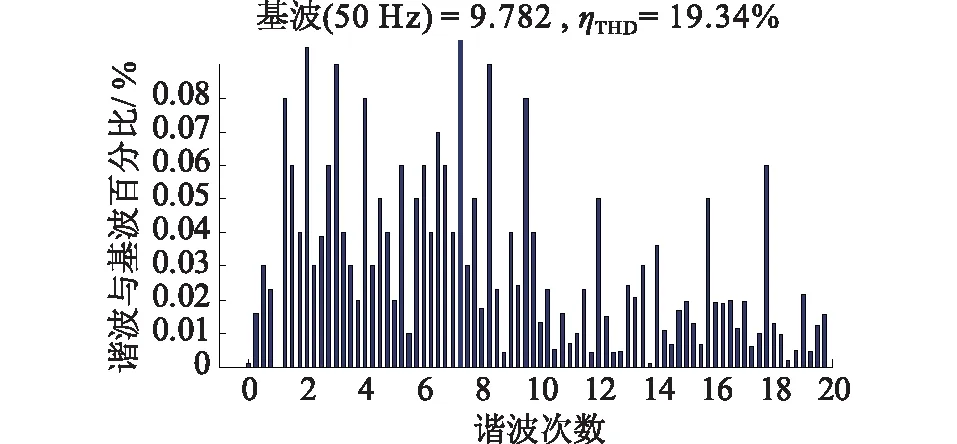
圖6 采用三角波控制時網側電流THDFig.6 The grid side current waveform THD of untaken measures

如圖7所示，采用了傳統無差拍控制策略，相比于圖5，網側電流波形趨于正弦，圖8是此時網側電流THD，圖中3至7次諧波含量降低，3至7次諧波補償率為60%，但仍較高，配電網運行仍受到危害。

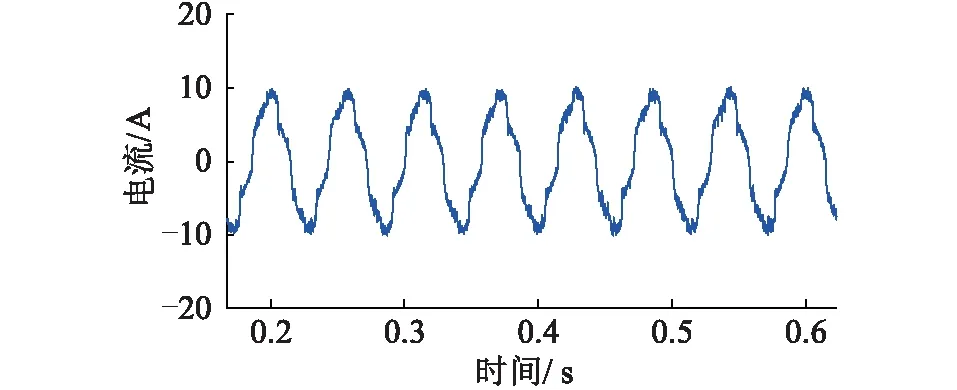
圖7 采用傳統無差拍后網側電流波形Fig.7 The grid side current waveform of adopt tradition deadbead

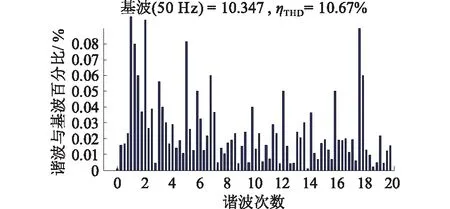
圖8 采用傳統無差拍后網側電流THDFig.8 The grid side current waveform THD of adopt tradition deadbead

如圖9、10所示，采用改進無差拍控制策略，從圖10中看出，此時網側電流THD為3.69%，圖中3至7次諧波都得到有效抑制，3至7次諧波補償率達到95%，系統運行安全性得到大大改善。

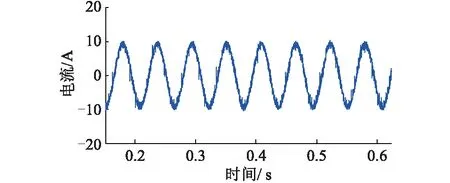
圖9 采用改進無差拍后網側電流波形Fig.9 The grid side current waveform of adopt improvement deadbead

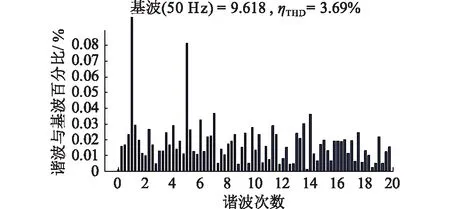
圖10 采用改進無差拍后網側電流THDFig.10 The grid side current waveform THD of adopt improvement deadbead

4 結語

文中以兩端柔直輸電系統為研究對象，建立兩端柔直數學模型，研究系統基本運行方式以及電壓源型換流器控制策略。考慮傳統無差拍控制運用于VSC換流器時具有控制延時以及電流閉環控制響應性差等問題，提出一種改進無差拍控制策略，通過預測k+2時刻采樣電流，解決上述缺陷。最后通過聯合仿真，驗證了所提方法的正確性與可靠性。未來可將文中所提改進方法與其他電能質量治理策略相結合，不僅拓寬了上述方法適用范圍，而且可以進一步提高系統穩定性。