非下采樣剪切波域抗錯性尺度不變的遙感圖像匹配算法

劉志強，朱立谷

(中國傳媒大學 計算機學院，北京 100024)

1 引 言

圖像匹配是指將兩幅或多幅圖像進行比較[1]，找到它們的共有景物。遙感圖像匹配在軍事和民用方面都具有重要的價值，但由于高分辨率遙感圖像信息量巨大，一般都有幾何畸變、地貌特征變化、地面雜波混入等影響，所以遙感圖像匹配更加困難。

隨著計算機技術的不斷發展，圖像匹配速度有很大程度上的提高，自動的歸納圖像匹配技術彌補了人工方法的不足，已經被廣泛地應用于遙感圖像匹配處理領域。

過去幾十年中，各種圖像匹配算法相繼出現[2-4]，且人們在結合許多數學理論和方法后不斷提出新的匹配算法，一般可分為基于灰度的匹配和基于特征的匹配。基于灰度的匹配方法直接根據圖像的灰度定義參考圖像和待匹配圖像之間的相似性度量。這些基于灰度的匹配算法計算簡單、易于實現，但是對圖像畸變的適應能力較弱，對遙感圖像匹配不能產生很好的作用。基于特征的匹配方法是先從待匹配的圖像和參考圖像中分別提取特征，然后在兩幅圖像的特征之間建立對應關系。匹配中常用的特征主要有點、邊緣、區域特征3種。點特征易于標示和操作，同時也反映了圖像的本質特征，所選取的興趣點是指相對于鄰域表現出某種奇異性的像素點。點特征容易提取，但所含信息量較少，所以建立兩幅圖像中特征點對應關系和保證適當的特征點數目是其難點所在。吳一全等[2]提出了一種利用Contourlet變換、Tsallis熵和改進粒子群優化的多源遙感圖像匹配算法。葉沅鑫等[3]針對多源遙感圖像間幾何變形和灰度差異造成的匹配難題，提出了一種結合SIFT和邊緣信息的匹配方法，相比直接利用SIFT自帶的特征描述向量，該算法有效地提高了匹配正確率。陳颯等[4]提出了一種基于Contourlet域Hausdorff距離和粒子群的多源遙感圖像匹配算法，實現了全分辨率情況下遙感圖像的匹配。為了進一步提高遙感圖像匹配的精度和運算效率。Zhang等[5]提出了一種基于特征點匹配的遙感圖像配準方法，利用特征點的三角形局部特征區域表示遙感圖像的局部特征，再利用KNN算法進行相似區域匹配，遙感圖像的特征表示魯棒性得到了提升，匹配精度也隨之得到改善。Shen等[6]利用以SIFT和歸一化互相關技術為基礎提出了一種新穎的遙感圖像匹配技術，提高了遙感圖像匹配精度基礎上，降低了時間復雜度。

基于此分析，本文提出一種非下采樣剪切波域抗錯性尺度不變的遙感圖像匹配算法。首先，利用非下采樣剪切波變換分解待匹配圖像獲得低頻子帶，采用抗錯性尺度不變檢測器提取分布均勻且穩定的特征點；然后，利用四元數指數矩提取出抗錯性尺度不變特征點局部特征區域的特征，并通過相似度計算進行預匹配。最后，通過隨機抽樣一致去除掉存在的錯誤匹配對。通過仿真實驗，證明了提出算法的有效性和實用性，顯著地提高了遙感圖像匹配的準確率。

2 提出的算法

2.1 特征點與特征區域

近些年，很多特征點檢測器被相繼提出，并廣泛應用于目標識別及圖像處理領域，例如SIFT(Scale-Invariant Feature Transform)特征點[7]、SURF(Speeded Up Robust Feature)特征點[8]等。上述特征點在目標識別和圖像配準領域得到了廣泛應用，但其魯棒性仍然偏低，尤其在圖像匹配中會嚴重降低精度。為解決此問題，本文將使用NSST域的SIFER特征點[9]作為遙感圖像感興趣點，提取出穩定的特征點，具體步驟如下：

1)對遙感圖像進行二級NSST分解，并提取低頻子帶；

2)在低頻子帶上創建尺度空間。在x，y方向上，對圖像進行n尺度濾波，先需要計算n+2個波長位置，公式如下所示：

(1)

若所求的連續波長之間差值小于2，則λj=λj-1+2，這樣做是為了避免在較小的波長位置為亞像素級采樣特征尺度而失去意義。計算與λ0，λ1，...，λn+1相應的濾波尺度σ0，σ1，...，σn+1。

(2)

其中，λ是基本正弦波的波長，σ是高斯窗口寬度，b表示半幅帶寬。

3)尺度空間濾波。調制高斯函數與余弦函數構造一維余弦調制的高斯濾波(Cosine Modulated Gaussian，CMG)表示為：

(3)

其中，φ表示濾波方向。這里將一維CMG拓展到二維CMG濾波，可以對圖像分別在x，y方向上進行濾波處理，得到的二維CMG濾波器：

CMGX(x，y；σ，λ)=e-(x2+y2)/2σ2cos(2πx/λ)

(4)

CMGY(x，y；σ，λ)=e-(x2+y2)/2σ2cos(2πy/λ)

(5)

4)尺度空間響應計算。利用公式(4)與公式(5)求出尺度σ0，σ1，...，σn+1上分別在x，y方向上的CMG響應，并分別表示為CMGX及CMGY，計算出在不同尺度上CMGX和CMGY的加和響應值Sj：

Sj=CMGXj+CMGYj

(6)

5)尺度空間極值檢測。在CMG加和響應的尺度空間內利用3×3×3的窗口提取極大值和極小值點：

Sj(×)>?Sj(·)，Sj(×)>?Sj-1(·)
Sj(×)>?Sj+1(·) ，Sj(×)Sj(×)

(7)

其中，“×”表示當前位置的響應之和，“·”表示相鄰位置的響應之和，通過公式(7)將判斷為極值點的位置作為候選的特征點。

6)去除邊緣響應。圖像邊緣區域通常會出現響應和的極值點，但這些位置并不是很好的特征點位置.步驟5就是用來去除邊緣響應的影響，實現去除邊緣區域的目的：

(8)

其中，x=(x，y)，gx=CMGX，gy=CMGY，W=λ，計算公式(8)里矩陣R的特征值的比：

eratio=γmax/γmin

(9)

(10)

(11)

通過eratio值來判斷出CMG加和響應中的極值點是否為出現在邊緣區域，如果候選特征點的eratio大于某個閾值時(本文算法中邊緣閾值選擇為6)，該點即被判定為邊緣點，則該點需要被剔除掉，而剩余的響應極值點就是最終剩余的SIFER特征點。

2.2 特征點提取與局部特征區域構造

通常局部區域可以構造成很多形狀，例如長方形、正方形、圓形和橢圓形等，但都需要能夠使構造的區域對局部去同步攻擊有很好的抵抗能力。本文自適應地構造出橢圓特征區域，相比較其他算法具有更好的魯棒性。橢圓區域的構造可以分成以下環節：

1)利用SIFER檢測器在宿主遙感圖像中提取出特征點，X(x，y)表示橢圓區域中心點。

2)通過公式(8)可以計算出二階自相關矩陣R(x)，然后根據公式(12)和(13)自相關矩陣R(x)的特征值(λ1，λ2)：

(12)

(13)

3)分別利用特征值(λ1，λ2)和特征向量(v1，v2)計算出局部橢圓區域的長軸ra、短軸rb和方向角θ：

(14)

2.3 四元數指數矩及穩定性能分析

本文中期望借助指數矩的優秀描述能力對遙感圖像局部特征區域進行描述，所以這里將結合四元數理論對指數矩陣進行改進，從而推到出適合于彩色圖像的四元數指數矩。

四元數作為復數的一種推廣[10]，由愛爾蘭數學家哈密爾頓正式提出。四元數表現為一種超復數形式，由一個實部和三個虛部組成，可以寫成如下表達式：

q=a+bi+cj+dk

(15)

其中，a、b、c和d都表示為實數，i、j和k表示三個虛數單位，并需要滿足以下規則：

i2=j2=k2=ijk=-1
ij=k，jk=i，ki=j
ji=-k，kj=-i，ik=-j

(16)

由上面的公式，可以把四元數的共軛和幅值的定義成如下形式：

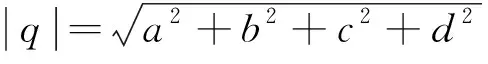
(17)

假設一個大小為M×N的彩色圖像f(x，y)具有紅色、綠色、藍色三個顏色通道，則可以用四元數形式表示為純四元數(沒有實數部分)，具體表示為：

f(x，y)=fR(x，y)i+fG(x，y)j+fB(x，y)k

(18)

其中，fR(x，y)、fG(x，y)和fB(x，y)分別代表了彩色圖像f(x，y)的紅色、綠色及藍色通道。這里面的i，j和k為虛數單位。

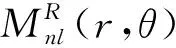
(19)

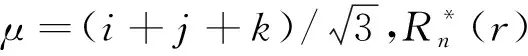
根據正交完整函數系理論，彩色圖像f(r，θ)可以通過有限階數的指數矩(n≤nmax，l≤lmax)近似重構回來，如果重構中矩的階數越多，重構回的圖像就更加接近原圖像，具體可以表示為如下形式：

(20)

結合指數矩和四元數理論，可以推導出四元數指數矩，同理，也可以得到四元數Zernike矩、四元數偽Zernike矩、四元數OFMMs，為了充分對比每種四元數矩的重構能力，進行了下面的重構實驗。

本文中利用四元數指數矩作為SIFER特征點的局部特征，除了良好的特征描述能力，四元數指數矩對常規信號攻擊和幾何攻擊均具有良好的抵抗能力。這部分將對四元數指數矩的幾何抵抗原理進行分析，具體如下所示。

2.3.1 平移不變性

首先計算一幅N*N圖像f(i，j)的質心(xc，yc)，并將圖像中心移到質心坐標位置，再計算其四元數指數矩，就得到了指數矩的平移不變性。

xc=m1，0/m0，0，yc=m0，1/m0，0

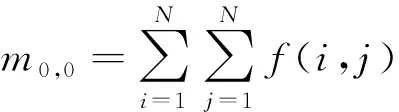
2.3.2 縮放不變性

設圖像函數為g(r′，θ)，找到圖像的半徑k，則r′的變化范圍為0≤r′≤k，其歸一化灰度圖像函數可表示為：f(r，θ)=g(kr，θ)=g(r′，θ)。其中，r=r′/k的取值范圍是0≤r≤1，f(r，θ)是經過歸一化的極坐標下圖像表示。此時，在極坐標系下通過f(r，θ)獲得的矩是縮放不變的，對于相同的f(r，θ)，在0≤r≤1范圍內，經過縮小或放大，對于任意f(r′/k，θ)都可以最終歸一化為同一個圖像函數f(r，θ)，所以歸一化后的彩色圖像四元數指數矩就具有了縮放不變性。

2.3.3 旋轉不變性

圖1給出了四元數指數矩(幅值)抵抗幾何攻擊能力的測試結果(128×128×8bit灰度圖像Barbara)。實驗結果表明，四元數指數矩的幅值具有很好的幾何不變特性。

2.4 提出的算法步驟

本文的核心步驟包括遙感圖像NSST低頻的SIFER特征點提取，局部區域四元數指數矩特征提取環節以及圖像配準環節。利用SIFER算子從NSST低頻提取出穩定性更高的遙感圖像特征點。考慮顏色通道間的相關性，充分利用了彩色圖像中重要的顏色信息，利用四元數指數矩幅值表示每個特征點的局部區域的特征，并將其構成特征向量進行初步相似度匹配。對于匹配出現的錯誤匹配對，通過隨機抽樣一致進行去除，有效地提高了遙感圖像匹配的精度。該算法引入了穩定性及特征表示能力的SIFER算子提取特征點，針對彩色的遙感圖像，利用顏色不變量理論充分考慮了重要的顏色內容，使提出的SIFER特征點更加穩定，利用指數矩作為每個特征點局部區域的特征提高了區域特的刻畫能力。該方案的基本流程圖如圖2所示。

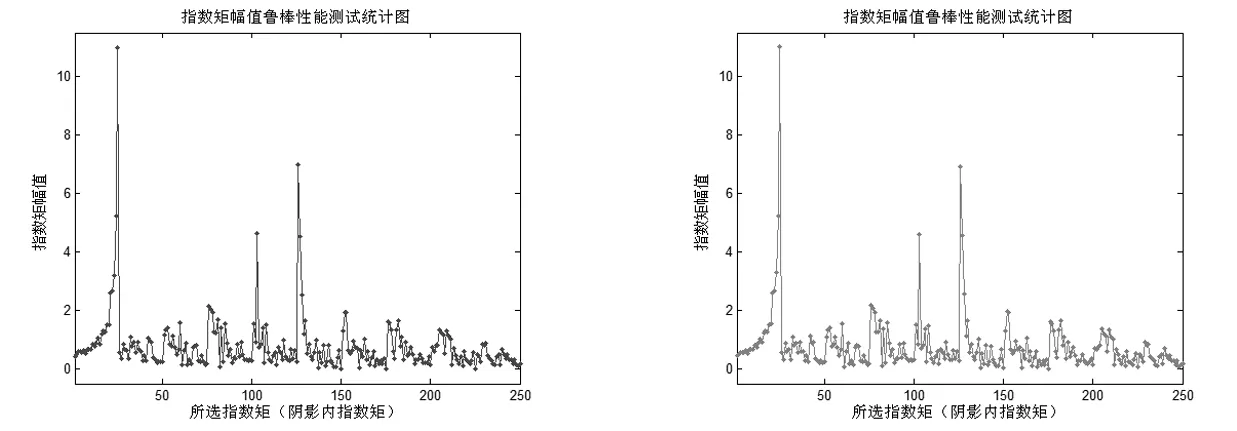
(a)無攻擊 (b)放大1.2

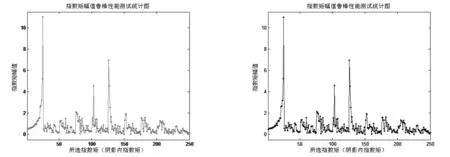
(c)縮小0.5 (d)旋轉15度

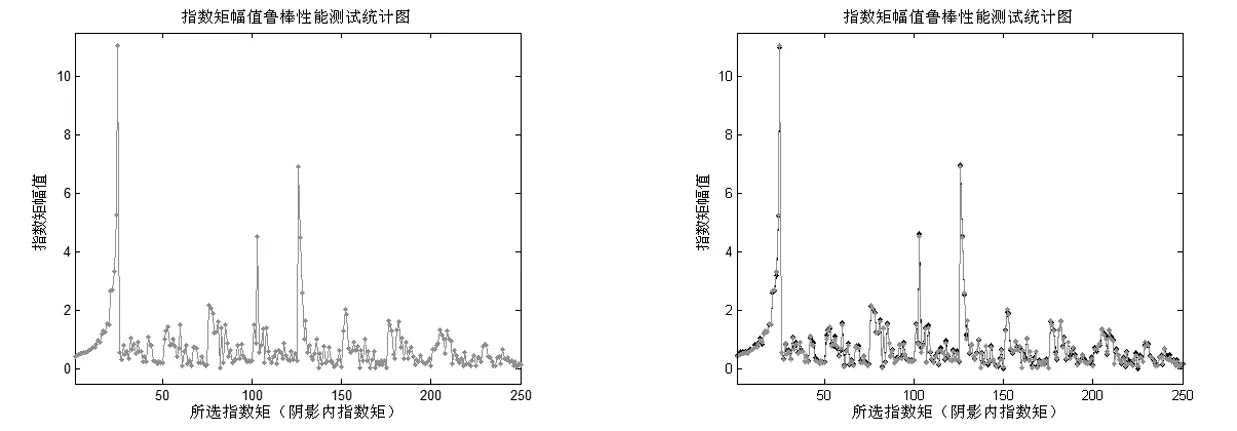
(e)旋轉30度并縮小0.7倍 (f)放大1.2、旋轉15度圖1 四元數指數矩(幅值)抵抗幾何攻擊能力的測試結果

3 實驗結果分析

分別利用SIFT遙感圖像匹配算法[11]、SURF遙感圖像匹配算法[12]和本文提出的算法，針對實際的遙感圖像進行實驗對比分析，所有算法均采用相同的特征表示方法以及RANSAC算法。實驗環境為8.0GB的RAM，3.80GHz的CPU，實驗平臺為Matlab 2015a。

評價標準使用檢測率用來衡量匹配性能的好壞，通過檢測率柱狀圖來客觀形象的展示檢測率的高低。檢測率(R)定義為正確匹配點對數和待匹配圖的點個數的比值：

(21)

實驗的參考圖像為谷歌地球下載的4幅可見光衛星遙感圖像，涵蓋北京地區4個不同類型的場景，分別如圖3所示，大小均為512×512。評價性能的指標包括匹配算法的抗擊何攻擊能力和抗常規攻擊能力。抗擊何攻擊能力中主要驗證算法的旋轉不變性和尺度不變性，在抗常規攻擊能力中主要驗證在椒鹽噪聲、高斯噪聲以及亮度變化下算法的匹配性能。

3.1 抗幾何攻擊能力測試

以圖3中居民區2圖像為例，將待匹配圖像分別旋轉20度，45度，70度，如圖4所示。將圖3中的參考圖像分別與攻擊后遙感圖像進行匹配，分析3種算法的抗旋轉能力，詳細對比結果見表1。

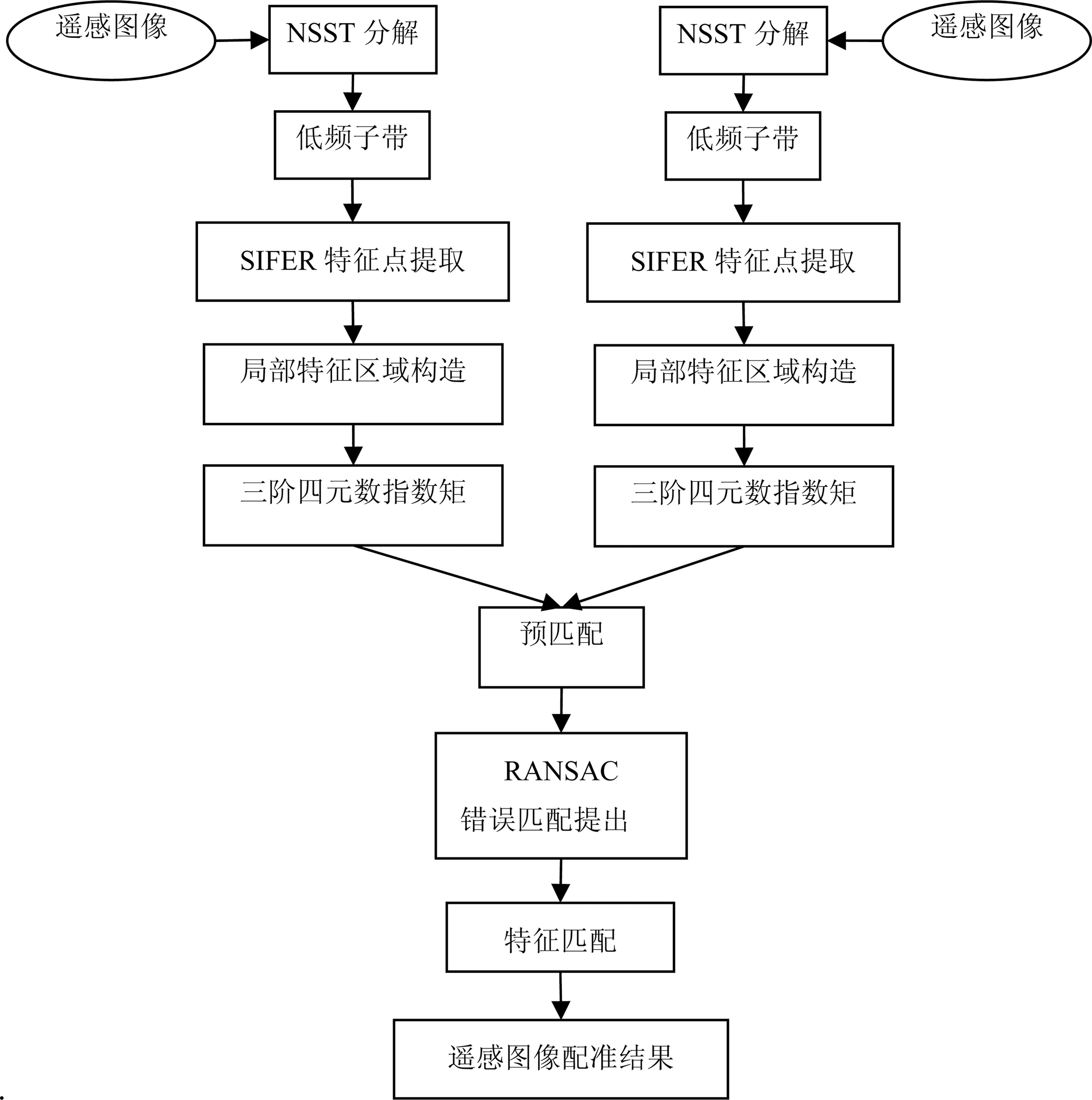
圖2 遙感圖像匹配流程圖

(a)居民區1 (b)體育場 (c)居民區2 (d)河流圖3 遙感圖像參考圖像

(a)旋轉20度 (b)旋轉45度 (c)旋轉70度圖4 旋轉后圖像

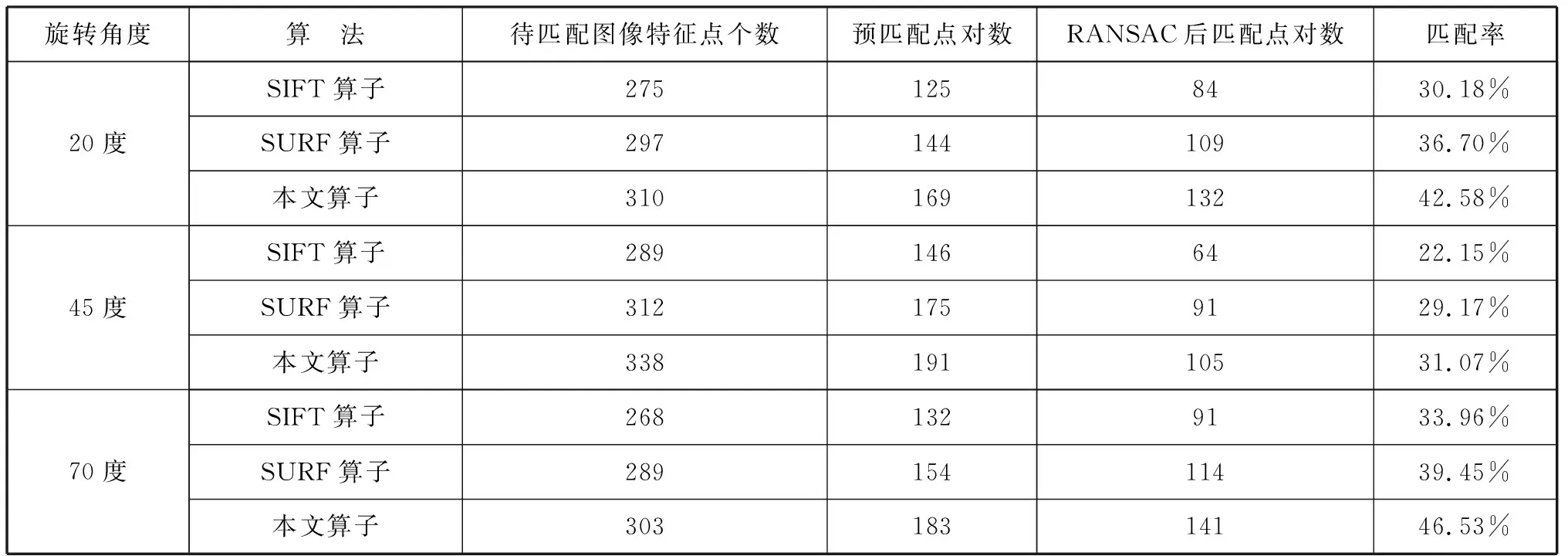
旋轉角度算 法待匹配圖像特征點個數預匹配點對數RANSAC后匹配點對數匹配率20度SIFT算子2751258430.18%SURF算子29714410936.70%本文算子31016913242.58%45度SIFT算子2891466422.15%SURF算子3121759129.17%本文算子33819110531.07%70度SIFT算子2681329133.96%SURF算子28915411439.45%本文算子30318314146.53%

以圖3中居民區2圖像為例，將待匹配圖像分別縮放0.5，0.7，1.5，如圖5所示。將參考圖像分別與攻擊后遙感圖像進行匹配，分析3種算法的抗縮放能力，詳細對比結果見表2。

由表1和表2綜合看出，本文算法抗旋轉能力最優，明顯高于SIFT算法和SURF算法。

3.2 抗常規攻擊能力測試

對三種算法的抗常規攻擊能力進行測試，如圖6中分別給出了添加椒鹽噪聲0.02，0.05，0.1以及高斯噪聲標準方差0.02，0.05，0.1的6幅測試圖像。

將參考圖像分別與圖7中各幅圖像進行匹配，分析3種算法的抗噪聲能力，結果如圖7所示。圖7(a)是3種算法對含高斯噪聲遙感圖像的匹配性能對比，橫坐標是噪聲方差，縱坐標是匹配率；圖7(b)是3種算法對含椒鹽噪聲遙感圖像的匹配性能對比，橫坐標是噪聲密度，縱坐標是匹配率。

(a)縮放0.5 (b)縮放0.7 (c)縮放1.5圖5 縮放后圖像

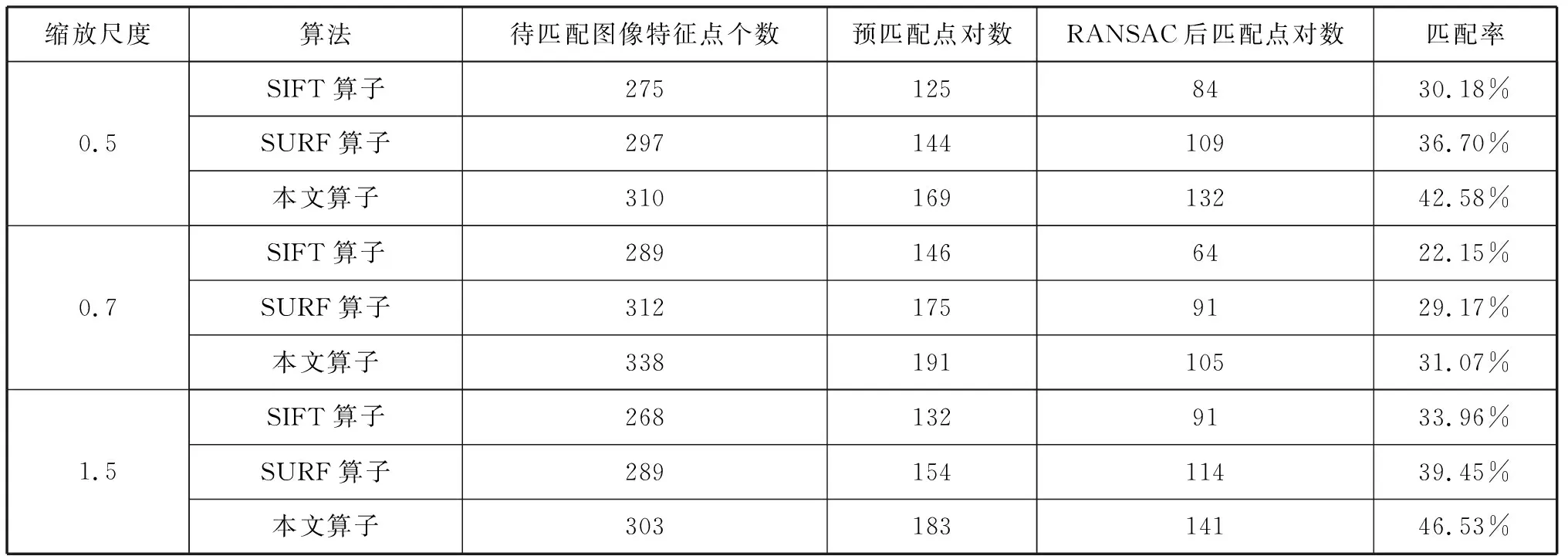
縮放尺度算法待匹配圖像特征點個數預匹配點對數RANSAC后匹配點對數匹配率0.5SIFT算子2751258430.18%SURF算子29714410936.70%本文算子31016913242.58%0.7SIFT算子2891466422.15%SURF算子3121759129.17%本文算子33819110531.07%1.5SIFT算子2681329133.96%SURF算子28915411439.45%本文算子30318314146.53%

(a)椒鹽噪聲0.02 (b)椒鹽噪聲0.05 (c)椒鹽噪聲0.1

(d)高斯噪聲0.02 (e)高斯噪聲0.05 (f)高斯噪聲0.1圖6 添加椒鹽噪聲和高斯噪聲后圖像

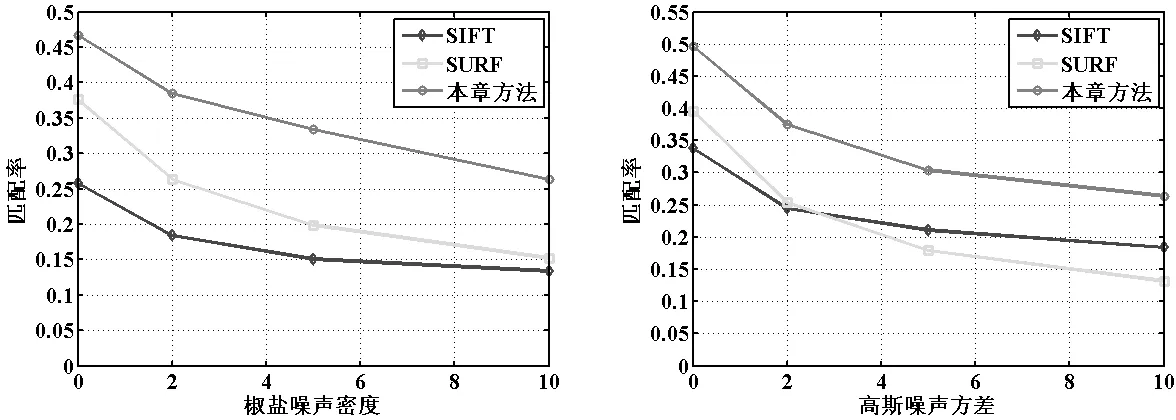
(a) (b)圖7 不同噪聲下匹配結果對比

由圖7可知，雖然在不含噪聲的情況下，SURF算法的匹配率低于SIFT算法，但隨著高斯噪聲方差/椒鹽噪聲密度的增加，SIFT算法的匹配率在大幅下降，幅度遠高于SURF算法，甚至最后匹配率會低于SURF算法，抗噪能力明顯不如SURF算法；而本文算法不僅在無噪聲的情況下匹配率最高，優于SIFT算法和SURF算法，而且抗噪性能也最好，匹配率始終保持對其他兩種算法的絕對優勢。這是因為NSST把圖像分解成1個低頻分量和多個不同方向的高頻分量，低頻分量基本保持了原圖的整體特征，而高頻反映了圖像的細節，含有大部分的噪聲，如果匹配的時候把高頻也考慮進去，不但常常受高頻噪聲的影響而產生誤匹配，而且匹配分析的時間消耗也很大。而本文只對圖像低頻分量進行匹配，可以大大降低噪聲等細節的影響，使得算法既提高了匹配的速度也提高了匹配的精度。

對待匹配圖像處理，構造中、低、高3種不同亮度，如圖8所示。其中，圖8(b)由(a)亮度降低4倍所得，(c)為(a)亮度提高2倍所得。將參考圖像分別與圖8中各幅圖像進行匹配，分析3種算法的抗亮度變化能力，詳細對比結果見表3。

由表3可知，在不同的亮度情況下，3種算法提取到的特征點數目基本保持不變，只是隨著亮度增加而略有增加；當亮度較低時，只有SIFT算法的匹配率略有下降，SURF算法和本文算法基本不變；當亮度較高時，3種算法的匹配率都有所降低，但SIFT算法下降幅度最大，SURF算法次之。由此得出，本文算法抗亮度變化性能最好，SURF算法次之，SIFT算法最差。

圖8 不同亮度下遙感圖像

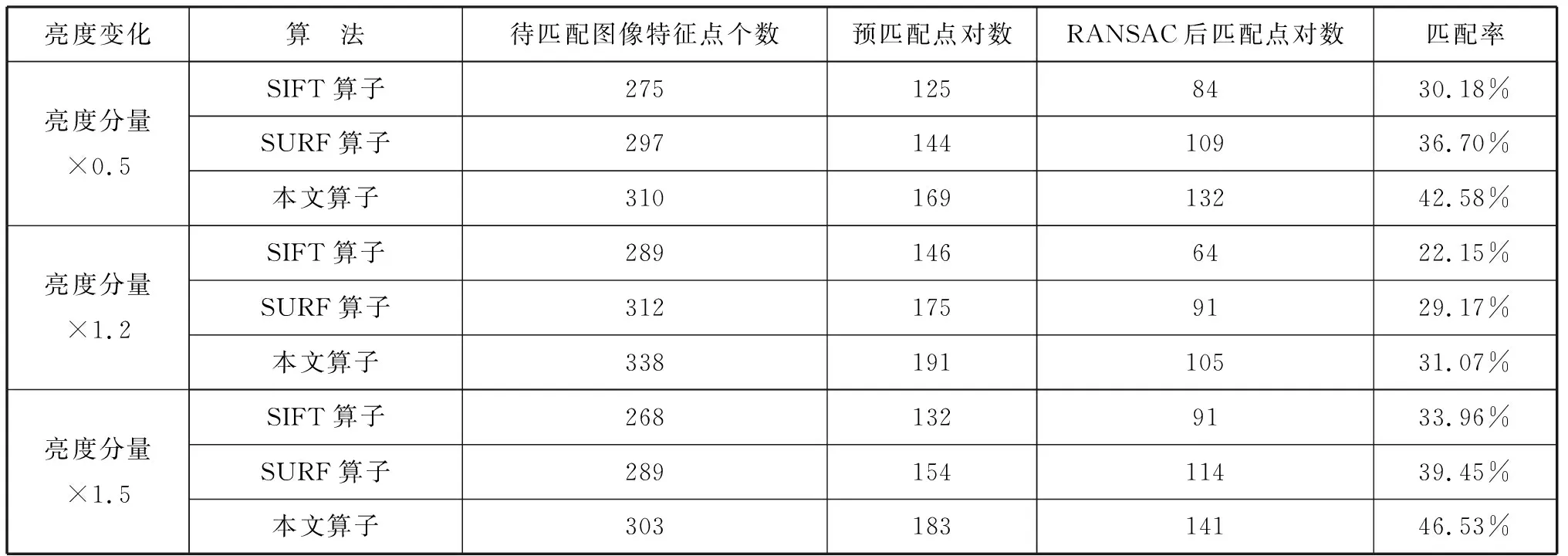
亮度變化算 法待匹配圖像特征點個數預匹配點對數RANSAC后匹配點對數匹配率亮度分量×0.5SIFT算子2751258430.18%SURF算子29714410936.70%本文算子31016913242.58%亮度分量×1.2SIFT算子2891466422.15%SURF算子3121759129.17%本文算子33819110531.07%亮度分量×1.5SIFT算子2681329133.96%SURF算子28915411439.45%本文算子30318314146.53%

4 總結

本文提出一種非下采樣剪切波域抗錯性尺度不變的遙感圖像匹配算法。首先，利用非下采樣剪切波變換分解待匹配圖像獲得低頻子帶，采用抗錯性尺度不變檢測器提取分布均勻且穩定的特征點；然后，利用四元數指數矩提取出抗錯性尺度不變特征點局部特征區域的特征，并通過相似度計算進行預匹配。最后，通過隨機抽樣一致去除掉存在的錯誤匹配對。