熱耗散變形下干氣密封角向擺動穩定性的研究

張偉政， 席喜林， 李水平， 陸俊杰， 丁雪興

(蘭州理工大學 石油化工學院，蘭州 730050)

干氣密封是一種新型的密封形式，其中常用的螺旋槽干氣密封有低泄漏、低功耗、長壽命和高穩定性等優點，在化工機械設備上得到了廣泛的應用，同時引起了國內外專家學者的研究興趣[1-2]。干氣密封是一種非接觸式機械密封[3]，動靜環兩端面間會形成一層厚度為3～6 μm 且具有一定剛度的氣膜，使得密封環端面不發生接觸，保持穩定運行。若間隙發生微小變化，極有可能使密封端面接觸摩擦，產生熱力變形，劃傷和磨損，嚴重時甚至發生干氣密封失效。因此，有必要對干氣密封的穩定性進行深入研究。

近幾年，國內外專家學者先后做了大量的工作。Zhang等[4]考慮了3個自由度下的干氣密封振動模型，建立了微擾運動方程，獲得了密封環的動態特性。Thatte等[5]研究了超臨界CO2渦輪機械設備用干氣密封的運行情況，計算極坐標下可壓縮雷諾方程獲得動靜環之間的氣膜剛度變化特性。Lee等[6]利用有限元的方法求解了螺旋槽干氣密封在非穩定狀態下的氣膜承載力、氣膜壓力和泄漏量等變化規律。Kollinger[7]通過試驗測試了軸向振動對一個穩定氣體潤滑機械密封的影響。Miller等[8]分析了螺旋槽端面在軸向和角向上的密封環運動，使用直接數值的頻率響應方法和瞬態雷諾方程，求得了相關的氣膜剛度與阻尼特性。Zhou等[9]搭建試驗臺，研究了非接觸螺旋槽機械密封的磁流體薄膜的潤滑特性，獲得密封承載力與外部磁場強度的關系。丁雪興等[10-11]對3種不同螺旋角的螺旋槽干氣密封氣膜振動位移進行測量，分析了其穩定性，并建立軸向密封系統振動模型求解失穩域范圍。張偉政等[12]建立了角向振動下氣膜-密封環系統模型，獲得了密封系統穩定時的結構參數區域。劉蘊等[13]利用ANSYS Workbench軟件對螺旋槽型干氣密封系統的動力學特性進行分析，解釋了振動趨勢形成的原因。劉占生等[14]建立浮環密封和轉子瞬時運動關系，基于有限元單元法求解瞬態流體壓力并考慮了失穩現象。

學者們從機理、數值計算、測試等多方面分析了密封動態特性和穩定性，但是考慮微尺度熱耗散以及變形對干氣密封系統動態穩定性的影響還相對匱乏，尤其在角向擺動問題上。

本文考慮非線性振動、微尺度效應和熱耗散變形的影響，研究螺旋槽干氣密封系統角向振動問題，分析干氣密封穩定運行的螺旋角范圍。同時，通過試驗觀察不同螺旋角對端面的影響，從而判斷熱耗散變形下的螺旋角范圍對干氣密封穩定運行的影響。

1 干氣密封理論計算的分析模型

1.1 干氣密封的工作原理

圖1所示為干氣密封常見的結構形式—雙端面(背靠背)。雙端面干氣密封主要由彈簧、彈簧座、靜環、動環、動環軸套、O形圈和密封腔構成。氣體從密封腔通入干氣密封，動環表面開設了微米級的螺旋槽，同時在轉速和壓力的作用下，氣體在螺旋槽內壓縮形成動壓效應，并且在靜環背壓和彈簧的作用下達到力平衡，使得動靜環兩端面之間被推開形成一層3～6 μm的氣膜剛度。

1.2 物理模型

干氣密封密封環之間的氣膜可以看做窄縫間的氣體流動，動環和靜環是窄縫的上下端面，同時3～6 μm窄縫需要考慮氣體的稀薄效應[15]。根據流體在窄縫中流動的特點，結合氣膜密封的特殊之處，作出以下基本假設：

(1)等溫，等黏度；

(2)氣體為理想氣體；

(3)氣體作層流運動；

(4)忽略氣體的慣性力與體積力；

(5)氣膜流速進入滑移區。

1.3 幾何模型

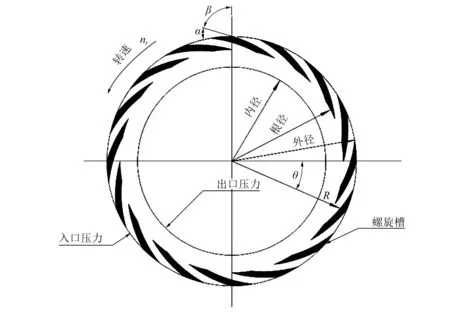
圖2 密封動環螺旋槽結構Fig.2 Schematic of the spiral groove

圖2為螺旋槽干氣密封動環，螺旋槽由對數螺旋線構成，并且周向分布。氣體利用微尺度槽道的動壓效應形成氣膜力，影響螺旋槽動壓效應的有以下三個關鍵參數：槽數、螺旋角、槽深，三個參數控制著螺旋槽的壓力、剛度、穩定性、泄漏量等一系列密封特性[16]。利用光纖激光打標機對動環表面進行加工，螺旋槽為槽區，非槽區稱為密封臺區，圖中Ro是密封環外半徑，Ri是密封環內半徑，Rg是密封環根半徑，α是螺旋角，β是螺旋角的余角，n為槽數，2E是螺旋槽槽深。

1.4 數學模型

干氣密封氣膜理論的基礎是流體力學,其控制方程是納維-斯托克斯方程。根據干氣密封幾何模型和速度滑移，氣膜的二維雷諾方程：

(1)

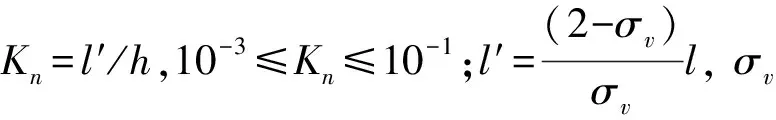
根據1.2節的假設和理想氣體狀態方程，可將式(1)寫成：

(2)

為了便于后續的理論分析，將式(2)進行無量綱，獲得了無量綱下的雷諾方程：

(3)

2 干氣密封相關基本方程的建立

2.1 振動方程

根據干氣密封的工作原理，對圖3所示的角向擺動模型提出以下假設：

(1)氣膜與密封環在運行中都具有振動位移變化，因此將振動模型設定為雙自由度；

圖3 角向擺動模型Fig.3 The model of angular vibration

(2)氣膜具有一定的剛度，因此將氣膜轉換成具有非線性剛度的彈簧；

(3) 動環跟軸共同旋轉，其位移設定為簡諧運動。

振動方程：

(4)

2.2 熱耗散下的氣膜能量方程

圖4為氣膜微元體熱量傳導模型。穩態下，由對流換熱過程控制方程組推導氣膜的能量方程[17]。

圖4 氣膜微元模型Fig.4 A micro control element

則微元體在單位時間內由擴散所吸收的熱量為：

(5)

單位時間內控制體由對流作用得到的熱量為：

(6)

由于膜厚間隙相當小，所以dz向的能量主要以擴散形式進出氣膜。則在單位時間內由擴散所吸收的熱量為：

(7)

同時將流體黏性耗散作用所產生的熱量加入氣膜微元體[15]，根據能量守恒定理，最終氣膜的能量方程：

(8)

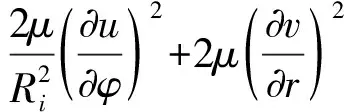
忽略溫度在氣膜厚度z方向變化,則氣膜的能量方程式(8)簡化為：

(9)

忽略耗散項，得到不考慮熱耗散下的氣膜能量微分方程：

(10)

2.3 氣膜厚度方程

干氣密封的動環采用SiC材料，靜環采用石墨材料。配對方式：硬環對軟環。在不同溫度和壓力下，動環的變形量遠小于靜環的變形量。因此，在進行變形計算時，只考慮靜環變形，動環變形忽略不計。

干氣密封靜環軸向熱彈變形為[18]：

δta=aLbfCR

(11)

式中：L為密封環長度;bf是密封面寬度;a是線膨脹系數；CR=ΔT/bf是溫度梯度。

干氣密封運轉下，若靜環無變形時，密封端面間的氣膜厚度均厚定值hb；但是當靜環發生變形時，氣膜厚度hb為變量，其表達式為：

hb=hmin+Δ=hmin+δmax-δ

(12)

式中：δmax為靜環變形最大值，hmin為氣膜厚度最小值，如圖5所示。

圖5 氣膜厚度結構簡圖Fig.5 The structural diagram for the gas film thickness

利用PH線性化方法和復函數分離變量法，將式(3)變為線性微分方程；隨后采用迭代法近似求解方程[19]，獲得氣膜開啟力：

(13)

靜環由于熱耗散發生了變形，均厚下的氣膜變為了兩頭寬中間窄，從而打破了干氣密封原有的平衡狀態，根據工作原理，氣膜開啟力Fo等于密封閉合力Fc：

Fo=p0A+Fe

(14)

式中：A為靜環面積(m2)，Fe為彈簧力(N)。

3 密封系統穩定性分析

3.1 計算實例

應用PH線性法和變分法，得到了角向位移微擾下的氣膜反作用力的增量，再利用復變函數和迭代法對氣膜邊值問題進行求解。由于角向微擾量為復數(K=η(η1(ζ)+η2(ζ)i)e-iω)，所以雷諾方程的微擾動態壓力是復變量，其實部和虛部就分別對應了氣膜的剛度和阻尼[20]。

微擾動態壓力的復數實部Re{K}=η(η1cosω+η2sinω)得到無量綱氣膜剛度的計算式：

(15)

微擾動態壓力的復數虛部Im{K}=η(-η1sinω+η2cosω)得到無量綱阻尼的計算式：

(16)

式中：

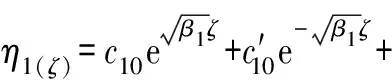
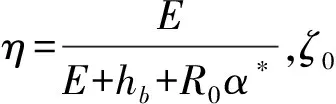
由此，氣膜角向擺動剛度：

(17)

阻尼：

(18)

表1為螺旋槽結構參數，表2為運行工況參數。

表1 螺旋槽結構參數

表2 運行工況參數

聯立(13)和(14)，得到氣膜的最小厚度為3.82 μm。將氣膜厚度進行逐段計算，分別得到含有氣膜非線性剛度和阻尼的兩個多項式。由于影響非線性氣膜剛度的因素較多，忽略密封加工和安裝誤差，和旋轉設備自身問題，只考慮結構參數對其影響，而螺旋角是體現對數螺旋線和控制線型方向的關鍵參數。所以對振動敏感參數螺旋角作為變量來研究分岔問題。

擬合氣膜非線性剛度：

K*=(α×0.291 069×1018-0.379 745×1018)×x2+
(α×0.234 142×1014-0.305 479×1014)×x-
(0.821 755×109+α×0.629 844×109)

(19)

擬合氣膜非線性阻尼：

Cg=(-α×0.585 365×1017+0.774 43×1017)×x2+
(-0.469 328×1013×α+0.620 945×1013)×x-
α×0.125 762×109+0.166 398×109

(20)

3.2 Floquet指數法對方程化簡求解

將式(19)、 (20)代入式(4)中，兩邊同除以J得：

(21)

式中：

c0=c/J,

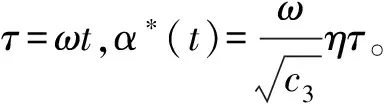
則方程變為：

(22)

簡化得：

(23)

其中：

(24)

3.3 熱耗散變形下的分岔問題的螺旋角范圍

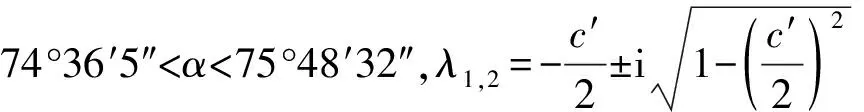
當c′=2時，α=74°36′5″時，λ1,2=-1為相等的負數，平衡點為臨界結點。

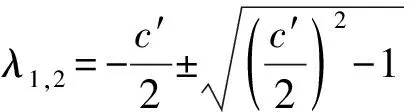
當c′=1時，α=75°48′32″時，λ1,2=±i為純虛數，解的曲線是極限環，如圖6所示，說明螺旋槽干氣密封發生Hopf分岔。

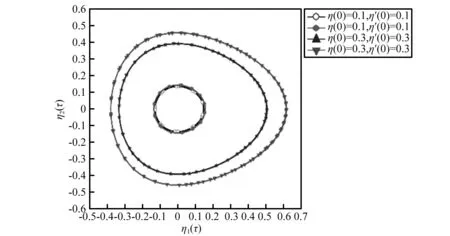
圖6 相圖Fig.6 Phase plane

以上針對干氣密封系統的穩定性進行了分析，當螺旋角74°36′5″<α<75°48′32″范圍內，干氣密封系統是穩定運行的，當螺旋角為α=74°36′5″和α=75°48′32″時，是干氣密封系統穩定運行的臨界點。當螺旋角α<74°36′5″或α>75°48′32″情況下，系統運行將會不穩定。

3.4 無熱耗散變形下的分岔問題的螺旋角范圍

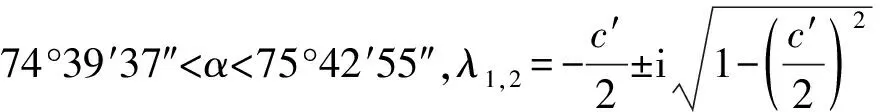
當c′=2時，α=74°39′37″時，λ1,2=-1為相等的負數，平衡點為臨界結點。

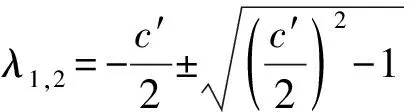
當c′=0時，α=75°42′55″時，λ1,2=±i為純虛數。解的曲線是極限環，發生Hopf分岔。

對比有無熱耗散變形下的計算結果發現：熱耗散變形下發生分岔問題的螺旋角范圍比無熱耗散變形廣；同時，分岔點位置要比無熱耗散變形下更大。這種螺旋角失穩域的變化，說明考慮熱耗散下氣膜-密封環流固耦合系統穩定性研究對螺旋槽干氣密封的穩定運行和優化指導具有重要作用。

4 試驗測試與分析

4.1 測試系統

本次試驗的測試系統分為四大系統：傳動系統、供氣系統、測試系統和密封系統，如圖7所示。

圖7 測試系統臺Fig.7 Photograph of the test bench

傳動系統由電機、軸承箱、主軸等組成， 0～10 000 r/min范圍內自由調控。供氣系統由流體無縫鋼管、壓力表、流量計、溢流閥等組成，使用范圍為：0～15.0 MPa。測試系統由傳感器、信號調理模塊、數據采集卡、計算機、軟件等組成，監控密封系統的工作狀態。干氣密封測試系統的原理圖如圖8所示。密封系統由雙端面干氣密封組成，采用雙端面干氣密封目的在于便于拆裝，避免對動靜環表面造成損傷。

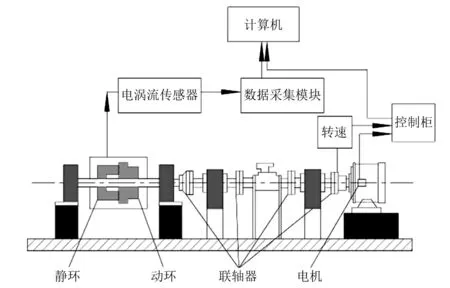
圖8 測試原理圖Fig.8 Schematic drawing of test bench

4.2 測試原理

采用常州雙環廠生產的金屬管浮子流量計LZZ-15/1/RR1/A/M1對泄漏量進行測量。通過氣路系統對密封端面進行通壓，并通過減壓閥保持壓力恒定，進氣補充氣量為端面泄漏量。

本次試驗采取表1中的參數，對密封環進行加工，動環采用SiC材料，靜環采用石墨材料。動環的結構根據螺旋角的角度差異而有所不同，螺旋角的選定依據來自于文中熱耗散變形下的螺旋角數值。兩個動環螺旋角分別設定75°50′為(非穩定下的螺旋角數值)，75°(穩定下的螺旋角數值)；兩個靜環的結構尺寸保持一致(分別為1號靜環和2號靜環)。選用的試件為干氣密封的“軟碰硬”結構，相對于“軟環”石墨環，“硬環” SiC環的硬度要遠大于石墨環，在試驗的過程中，SiC環的表面基本保持不變，可以忽略不計，故本次試驗只討論螺旋槽與石墨環表面的關系。

具體試驗步驟：

(1)將動靜環進行加工、刻槽、去毛刺飛邊、拋光、清洗和烘干，隨后進行裝配。75°50′動環與1號靜環配對，75°動環與2號靜環配對，準備兩套干氣密封雙端面樣機(1號樣機和2號樣機)。

(2)在實驗臺上安裝1號樣機，先往密封腔通入壓力，隨后進行盤車，確認無誤后，啟動電機進行升速，將壓力穩定在10.0 MPa，轉速穩定在10 000 r/min，觀察壓力表和流量計的變化。

(3)1號樣機運行30 min后，先停止轉速，再關閉壓力，將1號樣機進行拆卸，觀察靜環的表面變化情況。

(4)對試驗臺安裝的密封腔進行吹掃后，安裝2號樣機，操作步驟如同(2)和(3)。

(5)1號靜環和2號靜環對比分析，觀察兩者的端面 程度和泄漏量隨時間變化規律。

4.3 測試分析及對比

圖9為1號靜環端面，圖10為2號靜環端面。從兩張圖中能直觀得看到，1號靜環表面有嚴重的擦痕，甚至出現了磨損。擦痕呈周向均勻分布，區域恰好對應動環的槽區(外徑至根徑)，并且中間的擦痕更為明顯；2號靜環表面較為光整，看不出明顯的擦痕現象。

靜環表面擦痕的發生說明干氣密封的工作狀態是非平衡狀態；同時，擦痕分布的區域正是動環螺旋槽的動壓效應區，兩端面間沒有保持一層穩定而有效的氣膜剛度，使得動靜環的角向擺動變得更加劇烈，氣體在端面和槽區的運動加劇，從而導致動環和靜環在運行的過程中，會有間斷的碰撞和摩擦。另外，靜環端面中部的擦痕最為明顯，說明熱耗散下靜環發生了變形由于氣膜變為中間窄兩頭寬的形狀。所以，在不穩定的氣膜剛度、角向擺動和變形的共同作用下，對靜環表面造成了嚴重的傷害。

圖11為螺旋家75°50′和75°的干氣密封泄漏量，從兩者的泄漏量可以直觀的看到：75°的干氣密封在前10 min逐漸上升，隨后保持一個穩定的泄漏量數值，這是由于在剛開始運行的過程中螺旋槽干氣密封逐步脫開，密封間隙變大導致泄漏量增加，但是當氣膜開啟力和閉合力穩定時，氣膜剛度保持動態平衡使得泄漏量控制在一個穩定的數值，不存在穩定性下降和泄漏量增加的可能。但是，相比較75°50′的干氣密封，在運行的30 min內泄漏量不斷增加，從前期的緩慢增加到后期的急劇上升說明螺旋槽干氣密封發生了失穩導致泄漏量不斷上升，影響密封設備和旋轉機械的正常工作，造成此種現象的原因：螺旋角為75°50′的干氣密封在運行過程中，容易發生失穩，導致動靜環端面碰撞和變形，影響氣膜結構，導致泄漏量的不穩定性。起初運行時，端面的擦痕不明顯，造成的損傷較小，但是隨著運行時間的增加，端面擦痕和氣膜變形越來越嚴重，導致泄漏量上升速率增加。

若長時間運行，必定刮傷動環的槽區，導致泄漏量增大，嚴重時，將會降低干氣密封的使用壽命，出現安全問題。因此，考慮熱耗散變形下的螺旋角范圍，對干氣密封穩定性有一定程度的影響，說明了理論計算的準確性。在工程實際應用領域中，應盡量避免選擇出現密封系統分岔的螺旋角區域。

圖9 1號靜環端面圖Fig.9 No. 1 static ring face

圖10 2號靜環端面圖Fig.10 No. 2 static ring face

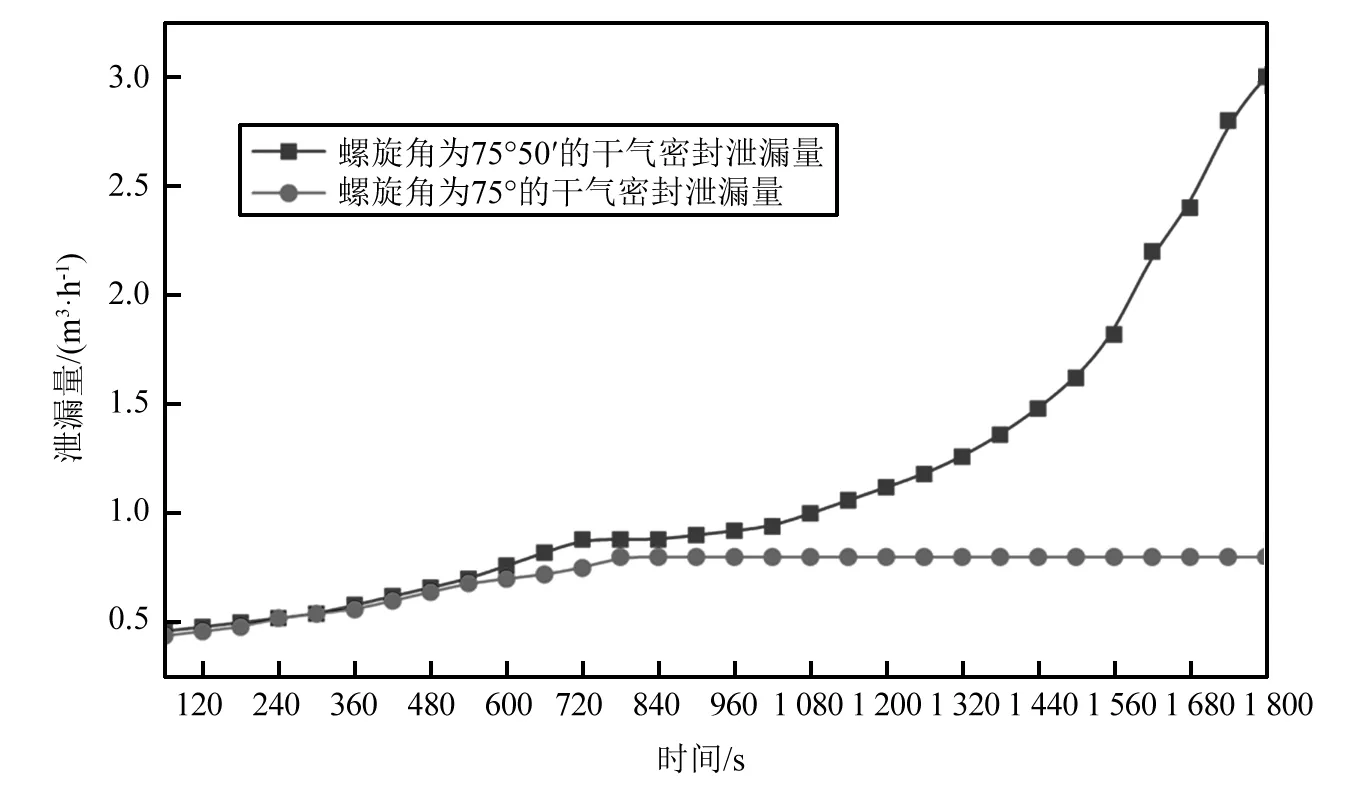
圖11 不同螺旋角的泄漏量隨時間變化Fig.11 Leakage of different spiral angles with time

6 結 論

本文考慮熱耗散變形研究螺旋槽干氣密封系統角向振動的穩定性問題，分析干氣密封系統發生分岔和穩定運行的螺旋角范圍，并且結合試驗分析，得到了如下結論：

(1)建立密封環雙自由度的振動方程，結合Floquet指數，求解了螺旋槽干氣密封發生失穩的螺旋角數值。耗散變形下的螺旋角為75°48′32″，無熱耗散變形下的螺旋角為75°42′55″，說明干氣密封系統發生分岔的位置有明顯變化，熱耗散對干氣密封的運行有一定的影響。

(2)從干氣密封穩定運行的螺旋角范圍來看，熱耗散變形的螺旋角范圍(74°36′5″<α<75°48′32″)相比較無熱耗散變形條件下的螺旋角(74°39′37″<α<75°42′5″)的區域更加明顯，說明對干氣密封螺旋角的選擇，需要考慮熱耗散對其影響。

(3)試驗表明了75°50′的干氣密封端面發生擦痕，而75°的密封端面保持光整，同時通過對比兩個不同螺旋角下的干氣密封泄漏量，可以發現75°50′下的泄漏量隨著擦痕的嚴重程度而不斷增加，而75°下的泄漏量在一段時間以后保持在穩定的數值，證明了考慮熱耗散變形對干氣密封系統的穩定性有一定的影響，從而驗證了理論計算的準確性。因此考慮熱耗散變形下密封動態穩定性的研究對工程實際有指導意義。

(4)今后研究干氣密封系統角向振動問題時，需耦合激振力或考慮外部存在激勵的情況，令計算結果更加精確，更加符合實際工程應用。