單人步行荷載模型研究

謝偉平， 章 濤， 何 衛， 馮金鵬

(1. 武漢理工大學 土木工程與建筑學院，武漢 430070；2. 武漢理工大學 理學院，武漢 430070)

隨著大跨輕柔結構的逐步發展，人致振動問題日益凸顯。對于該類問題的研究，重點和難點在于人行荷載的模擬，國內外學者們在該領域已開展了大量關于人行荷載模擬的研究工作。步行荷載模型有不考慮相互作用的時域力模型和考慮相互作用生物動力模型兩類。迄今為止，在該領域已經取得了較多的成果，現在面臨的問題是，對于現有的這些模型，我們該如何選取，以便更精確的預測結構動力響應，關于這一方面的研究，國內外尚未見文獻報道。本文基于最基礎的單人步行荷載，開展不同荷載模型的對比分析與實驗驗證工作，為單人步行荷載模型的選取提供參考。

人與大跨輕柔結構之間存在不可忽略的相互作用[8]，為了研究這種相互作用，人體被簡化為不同形式的彈簧、質量和阻尼(Spring Mass Damper, SMD)系統。Archblod[9]認為不考慮相互作用對于單人和人群響應預測都會偏于保守。Kim等[10]基于生物力學領域的雙足行走模型(Bipedal Walking Model, BWM)，提出了具有時不變阻尼的雙足模型。秦敬偉等[11]在Kim的基礎上進行改進，提出了具有時變阻尼和反饋機制的新雙足模型，使得每一步的起始足底反力能從零開始并且保持人體平衡。何衛，謝衛平等[12-13]分析了結構上人體對結構動力特性的影響，并基于雙足模型分析了人-結構相互作用對足底反力的影響。謝旭等[14]采用BWM對一人行橋的計算結果表明不考慮相互作用的計算結果明顯大于考慮相互作用的計算結果。丁陽等[15]基于靜止人體的兩自由度SMD模型[16]，構建了考慮相互作用的隨機人行荷載模型，其認為考慮相互作用會降低結構響應。Silva等[17]基于單自由度自激勵ASMD模型(Actuator Spring Mass Damper，ASMD)，通過實驗模態分析得到了人體行走狀態下的模型參數，簡化了人體行走模型。

對已有步行荷載模型進行評述，分析了模型各自的特點及適用范圍；在此基礎上，建立了包含亞諧分量自激勵的ASMD模型Ⅱ，并開展人致振動實驗對其進行了驗證。

1 步行荷載模型

不考慮相互作用的時域力模型有連續的傅里葉級數模型和單步落足“M”曲線兩種形式，SMD模型有BWM模型和ASMD模型，見表1所列。本節將對這五種步行荷載模型進行評述。

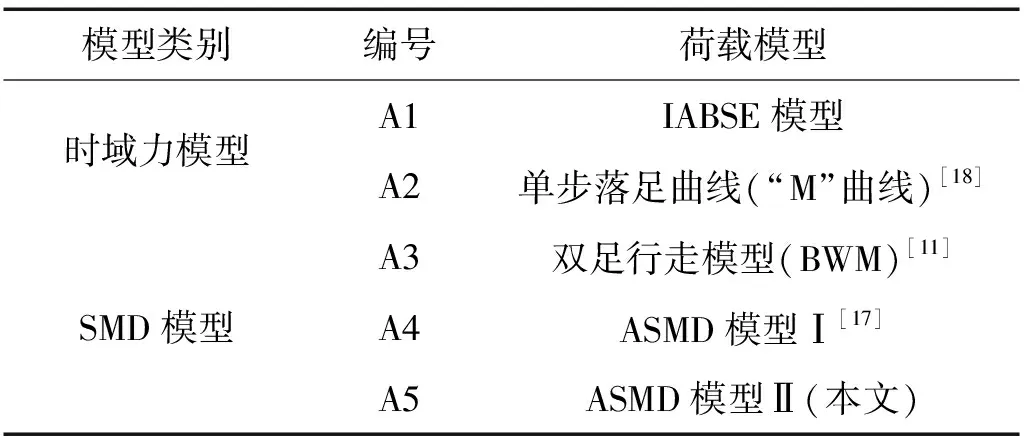
表1 人行荷載模型

1.1 不考慮相互作用的時域力模型

1.1.1 模型A1：IABSE模型

國內外學者對動載因子(Dynamic Load Factor，DLF)取值進行了豐富的研究工作，比較有代表性為Kerr和陳雋的實驗研究工作，兩者的研究結果均表明：在正常步頻范圍內，一階DLF的取值隨步頻的增大而增大，高階DLF與步頻相關性不明顯。

國際橋梁與結構工程協會(IABSE)推薦使用三階傅里葉級數模型來描述步行荷載，如式(1)所示。

(1)

式中：F(t)為步行荷載；G為人體自重；fp為步頻；t為時間；ai為第i階動載因子，φi為第i階諧波初相位，α1=0.4+0.25(fs-2)，α2=α3=0.1，φ1=0，φ2=φ3=π/2。

圖1為一階DLF隨步頻的變化關系，由圖可知，IABSE模型的一階DLF取值在低頻偏大，偏于保守考慮，以IABSE模型為連續傅里葉級數模型的代表進行后續分析。

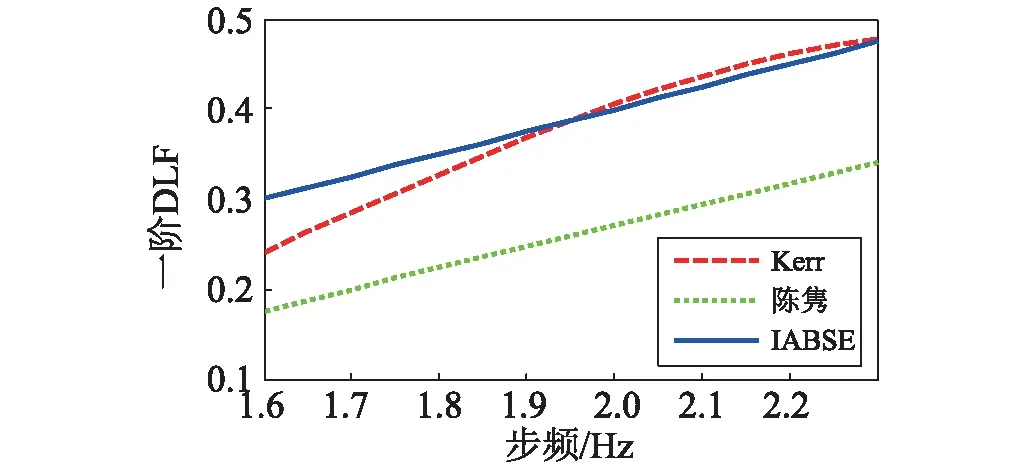
圖1 第一階動載因子 Fig.1 First order dynamic load factor

1.1.2 模型A2：單步落足曲線

單步足底反力表現為“M”曲線，其加載方式在空間上以步幅為增量，在每個落足點進行加載，表現為多點時滯激勵。聶建國和陳宇等基于Young提出的連續傅里葉級數模型，逆向構建了包含五階頻率分量的標準單步落足“M”曲線，表達式為

(2)

式中：F(t)為單步落足力；t為時間；αi為第i階動載因子；Te為單步足底接觸時間，Te=1/0.76fp，fp為步頻。

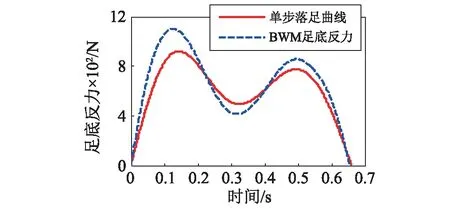
圖2 模型A2和A3足底反力 Fig.2 Ground reaction force of model A2 and A3

如圖2所示為體重80 kg，步頻為2 Hz時的單步落足力，模型A2相對IABSE模型而言，加載方式能更加真實的反映人行走過程中的空間變化和雙腿交替的過程，且不含初始相位，簡化了模型參數。

1.2 考慮相互作用的SMD模型

1.2.1 模型A3：雙足步行模型

BWM包含人體質量m、雙腿彈簧k、阻尼c、沖切角θ和腿長l，如圖3所示。BWM模型在行進過程中，每一步起始時刻人腿的軸向速度都不為零，Kim提出的腿部阻尼恒定假設會使得每一步的起始足底反力不為零。秦敬偉提出的具有時變阻尼和反饋機制特性的新BWM模型，使每一步的足底反力能從零開始并且保持人體平衡。

BWM與人體表觀特征相近，具有以下特點：

(1)BWM將腿部簡化為彈簧阻尼模型，通過支撐腿與隨動腿的轉換模擬人體系統的行走過程，產生的足底反力表現為單步落足曲線，與輕柔結構之間的相互作用會使得腿部收縮量增大，導致足底反力增大，如圖2所示。

(2)BWM輸入參數較多，且難以觀測(如腿的支撐剛度等)；模型相對復雜，對于人群響應的應用難于實現。

雙足模型數值程序驗證工作可見文獻[13]，此處不再贅述。

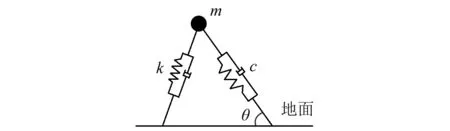
圖3 雙足行走模型Fig.3 Bipedal walking model

1.2.2 模型A4：ASMD模型Ⅰ

人體行走的過程中存在自激勵現象，學者們在單自由度SMD的基礎上，用簡諧力來表示內部自激勵，構建了具有內部自激勵的ASMD模型[19]來模擬運動人體，如圖4所示。圖中彈簧、質量塊和阻尼表示人-結構相互作用部分，A表示自激勵部分。

Sliva和Pimentel等以20名受試者為研究對象，將加速度傳感器安裝固定在其腰部，基于ASMD模型，通過實驗模態分析方法擬合得到了行走狀態下的模型參數m，c和k，見下式：

(3)

式中：mh為人體質量；fp為步頻；m，c和k為單自由度模型的質量、阻尼和彈簧剛度。

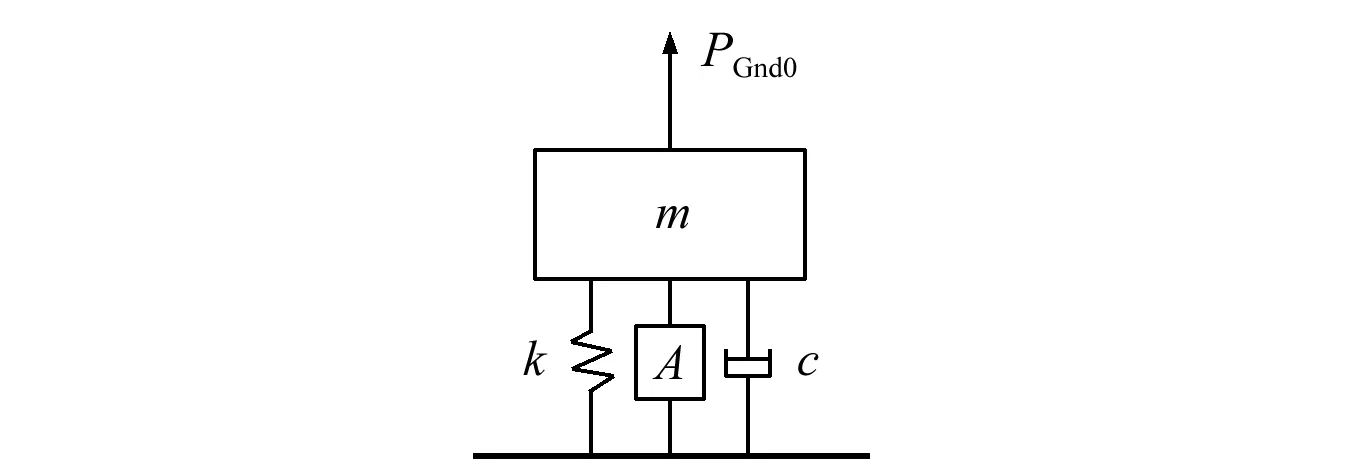
圖4 單自由度行走模型Fig.4 Single degree of freedom model for walking

Sliva等取Kerr的前三階傅里葉級數作為自激勵，如式(4)所示，構建了ASMD模型Ⅰ。

(4)

式中：A1(t)為自激勵，各參數的含義與模型A1相同，fp為步頻；第二、三階動載因子分別取值為0.07和0.05；第一階動載因子表達式為

(5)

圖5為人體質量為80 kg，步頻為2 Hz的ASMD模型和Matsumoto等[16]靜止站立模型的歸一化表觀質量幅頻特性。從中可知，ASMD模型與靜止站立模型不同，人體行走過程中只有部分質量參振。

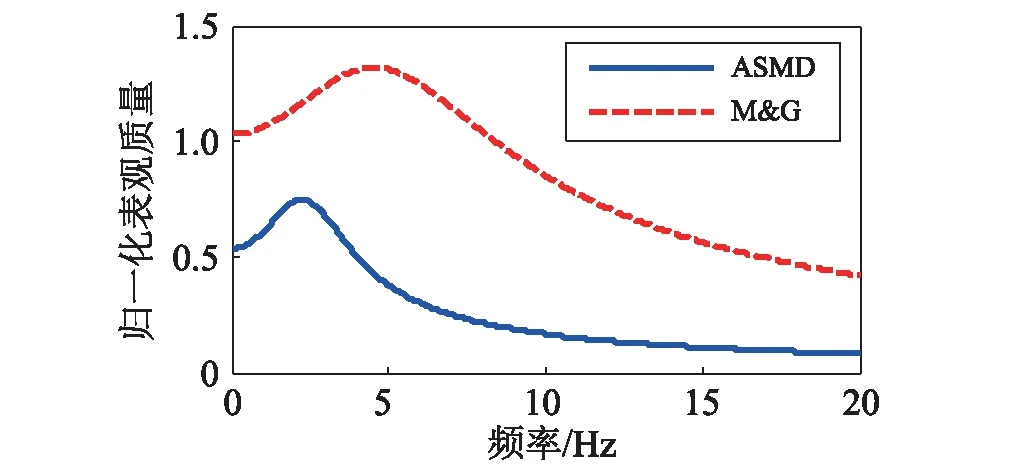
圖5 圖 5人體歸一化表觀質量幅頻曲線Fig.5 Normalized apparent mass response functions

1.2.3 模型A5：ASMD模型Ⅱ

Dey等[20]在輕型鋁橋上開展了人致振動實驗，實測響應中出現了顯著的瞬態振動，包含各階亞諧分量；采用不考慮亞諧分量的數值模擬結果瞬態響應十分微弱，不包含各階亞諧分量；其只對主諧動載因子的取值進行了修正，并沒有考慮亞諧分量。本文在輕質人行橋上進行單人行走實驗時也發現，實測響應中出現了顯著的亞諧頻率分量，且隨著人/結構質量比的增加，亞諧分量更顯著；在亞諧共振區時，模型A1、A2和A4的計算結果與實測結果相比偏小，且存在亞諧頻率成分缺失。

Zivanovic基于頻域逆向構建了包含多階主諧和亞諧分量隨機時域荷載模型，每次構建單人荷載需在[0,2π]之間隨機生成400個初相位，計算結果具有一定的離散性，需要獲取統計結果，應用起來比較復雜。為便于揭示上述實驗現象，在模型A4的基礎上進行改進，引入Zivanovic的亞諧分量，將模型A4中的自激勵改進為A2(t)，見式(6)，建立了ASMD模型Ⅱ。

(6)

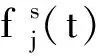
(7)

模型A5包含了由于雙腿交替不對稱產生的亞諧頻率分量，更加細致的反映了步行力特征。

2 荷載模型對比分析

將模型A1～A5應用到不同頻率的結構上，比較各模型結果之間的差異性。人體質量取85 kg，步頻為1.7 Hz，以模型A1為基準，只考慮二、三階倍頻共振，結構頻率變化范圍為2.0 ～ 5.5 Hz。雙足模型參數依據謝偉平等研究取值為：質量為85 kg，阻尼比為8%，剛度為21.25 kN/m，腿長取1.0 m，沖切角為69°，初始輸入能量為855.5 J。

定義標準加速度為：

as=apM0/mh

(8)

式中：as為標準加速度；ap為加速度峰值；M0為結構模態質量；mh為人體質量。

圖6為標準加速度計算結果，模型A5由于包含步頻亞諧分量，與其他模型相比存在亞諧共振區，從中可知：

(1)在亞諧共振區：除模型A3外，模型A5的計算結果與其他模型相比偏大；模型A3僅在二階亞諧共振區時，其計算結果才表現為偏大，在高頻區無明顯偏大現象，與秦敬業等的結論一致。

(2)在倍頻共振區：模型A1計算結果顯著大于A5，表明不考慮相互作用會放大結構共振響應，這與Archbold和丁陽的結論一致；模型A5在二階步頻共振區與A3結果相當，在高頻區共振區略大于其結果；A4的自激勵動載因子偏小，所以計算結果較小。

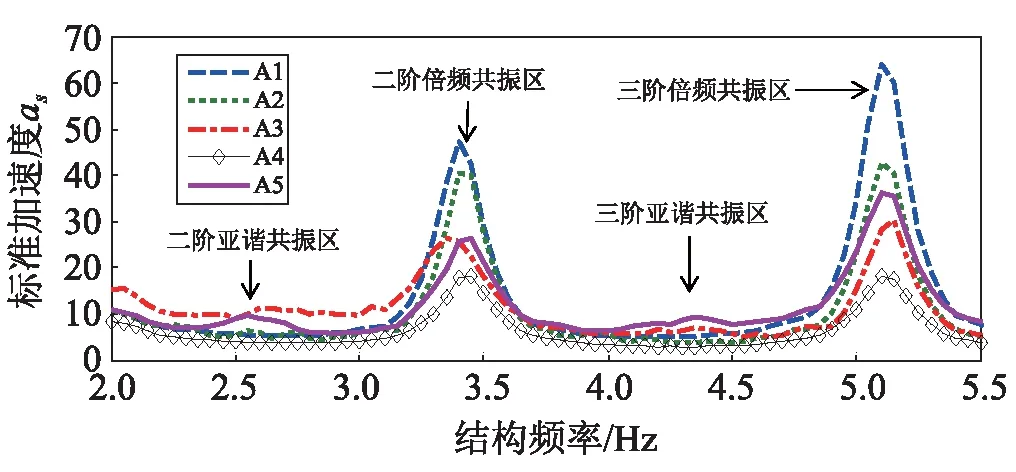
圖6 標準加速度計算結果Fig.6 The standard acceleration calculation results

3 荷載模型實驗驗證

本節在基頻不同的兩單跨簡支人行橋上進行單人行走實驗，驗證上節的數值分析結果和ASMD模型Ⅱ的有效性。

3.1 剛度較小人行橋

3.1.1 結構模型

人行橋全長10.5 m，兩邊簡支，計算跨度為10.3 m，寬1.0 m，該結構有未敷設混凝土和敷設混凝土前后兩種狀態，圖7所示為未敷設混凝土狀態。對敷設前后兩種結構進行模態測試，結構動力特性如表2所列。

圖7 人行鋼橋(未敷設混凝土)Fig.7 Pedestrian Bridge (without deck)

3.1.2 實驗結果分析

在節拍器的引導下，體重為85 kg的受試者S1在上述結構上進行了不同步頻下的單人行走實驗，實驗工況詳情及實測結果見表2所列，工況二為參考組。

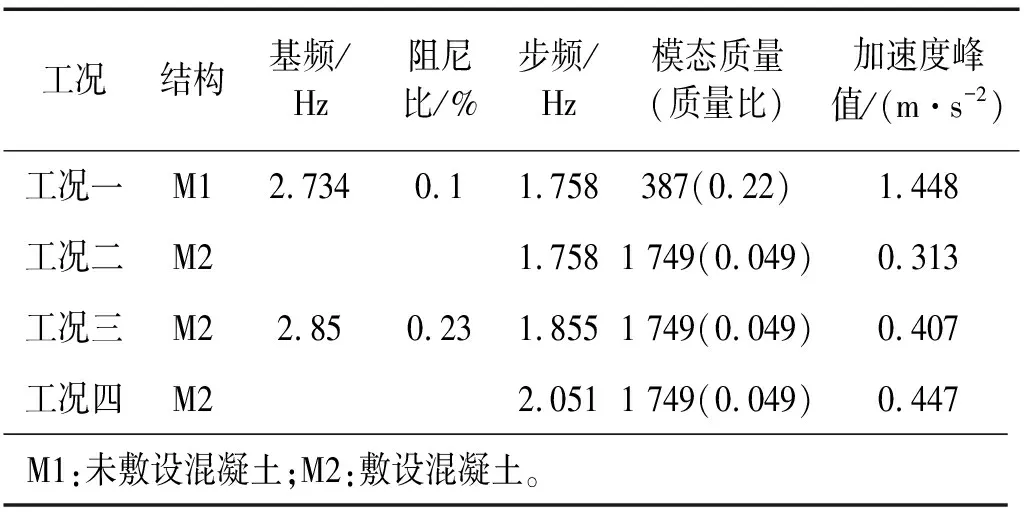
表2 實驗工況與結果

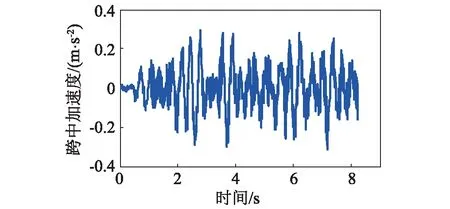
圖8 工況二實測結果Fig.8 Measured result in case 2

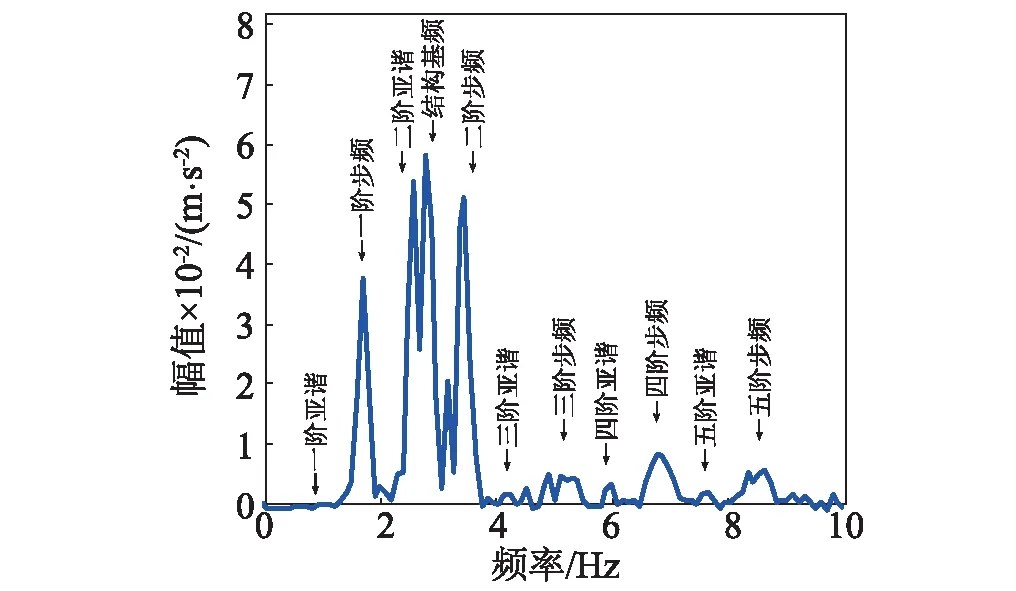
圖9 工況二實測結果頻譜Fig.9 Measured result spectrum in case 2

圖8和9為工況二實測結構跨中加速度響應時程和頻譜，由圖可知，響應頻譜中包含了多階主諧和亞諧頻率分量，亞諧貢獻突出。為了定量分析響應中亞諧分量的影響程度及變化規律，定義亞諧幅值比例系數μ和αi為：

式中：mi和si分別為響應頻譜在第i階主諧和亞諧頻率處的幅值。

圖10為四種工況下的比例系數μ和αi計算結果，由圖可知，四種工況中亞諧分量處所貢獻的結構響應幅值均占有較大的比重，比例系數μ高達37%～45%，其中以第二階亞諧分量(與結構基頻相近)占主導。工況一中各階亞諧分量幅值都比較顯著，與工況二相比可知，隨著人/結構質量比的減小，μ減小而α2增大，其余各階亞諧分量占比均減小。

以上分析表明：當人/結構質量比較大時，各階亞諧分量所貢獻的結構響應都會很顯著；隨著質量比的增加，亞諧分量的影響會減弱，并逐漸以基頻亞諧分量的影響為主。

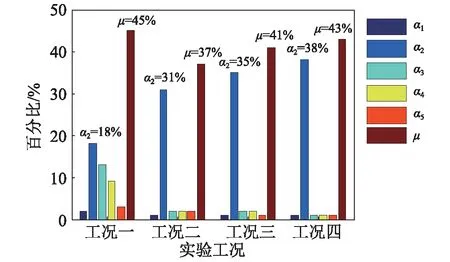
圖10 比例系數Fig.10 The coefficient of proportionality

3.1.3 荷載模型驗證

結構M1和M2的基頻落入亞諧共振區，采用模型A1～A5對上述四種工況進行計算。受試者S1的雙足模型參數為：質量為85 kg，阻尼比為8%，剛度為21.25 kN/m，沖切角為69°，腿長取1.0 m，工況一至四初始輸入能量為依次為：858 J、858 J、866 J和876 J。

表3為上述四種工況下各模型跨中加速度峰值計算結果，由表可知，模型A1、A2和A4忽略了亞諧分量，與實測結果相比，其計算結果明顯偏小，工況三中誤差達到最大，分別為-31.0%、-32.7%和-49.6%。模型A3計算結果整體偏大，工況一中誤差高達83.4%，這是因為結構頻率較低，模型A3與結構產生了顯著的相互作用所致。模型A5的計算結果與實測相比，工況三中誤差最大，高達13.02%；這是因為人體行走過程在一定程度上具有變異性，不能完全產生亞諧共振；相比之下，A5與實測結果吻合較好。

為了進一步驗證A5的適用性，令體重分別為60.5 kg、64.5 kg和73.5 kg的三受試者S2、S3和S4在節拍器的控制下，在結構“M2”上以亞諧共振步頻1.855 Hz行走。

表4為S2-S4的實測與數值結果，從中可知，A5的誤差在10% 以內，與實測結果吻合較好，其余模型的誤差與S1的結果一致。

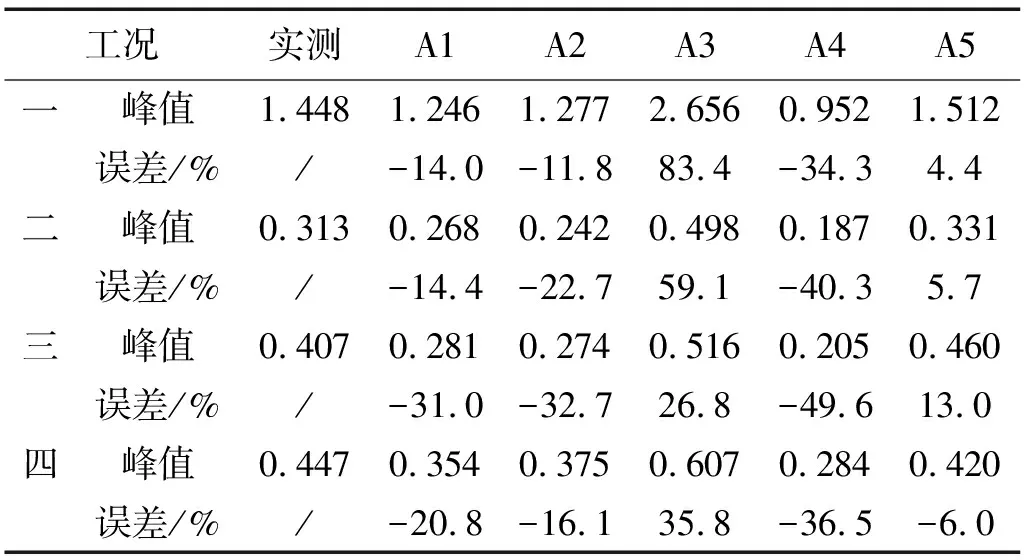
表3 S1的實測與數值結果

圖11為工況二的加速度時程和頻譜，模型A4與A1的頻譜特性相近，A2與A3的頻譜特性相近，故只給出了模型A1、A3和A5的頻譜。從中可知，模型A1～A4的頻譜基頻響應貢獻偏小，模型A5的基頻響應顯著，且包含相應的亞諧分量，與實測結果吻合較好。

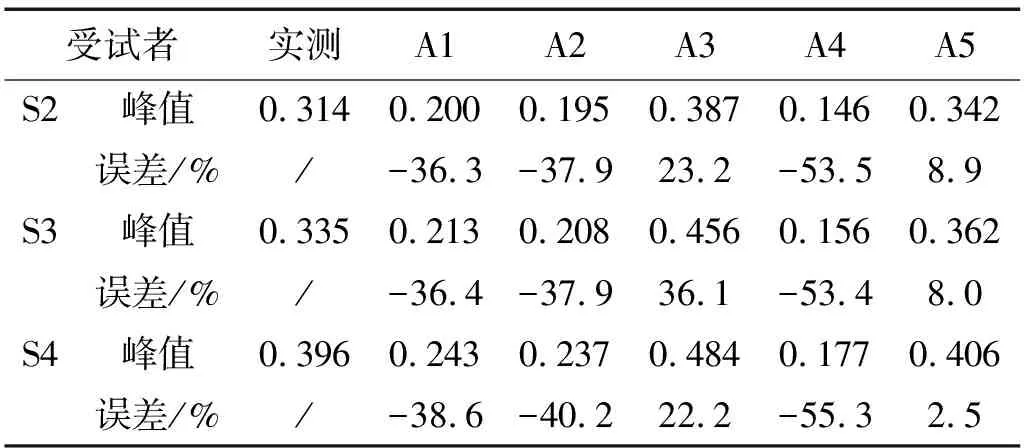
表4 S2-S4實測與數值結果

以上分析表明：當結構基頻落入亞諧共振區時，亞諧分量影響非常顯著，忽略亞諧分量，會導致計算結果偏小，模型A5在時頻域均與實測結果吻合較好。

圖11 工況二模擬結果Fig.11 Simulation results in case 2

3.2 剛度較大人行橋

將結構“M2”的跨度調整為8.4 m，經模態測試得結構基頻變化為4.297 Hz，記為結構“M3”，此時結構基頻落入二階步頻共振區，可進行倍頻共振驗證工作。使S2-S4在節拍器的引導下，在結構M3上以共振步頻2.148 Hz行走。

表 5 所列為實測與數值模擬結果，S4的跨中加速度時程圖和頻譜圖如圖12所示，由圖可知，結構產生了共振現象。由表可知，模型A1和A2的計算結果顯著偏大，平均高于實測結果70%以上，結果偏于保守；模型A3～A5的計算結果與A1和A2相比，與實測結果較為接近，A3的最大誤差為39.6%，A5最大誤差為34.5%，能更好的預測結構共振響應。

以上分析結果表明：不考慮人-結構相互作用的荷載模型，其共振響應預測結果會偏于保守；考慮相互作用的SMD模型能更好的預測結構共振響應，其中模型A5能在相對較小的偏差范圍內預測結構共振響應。

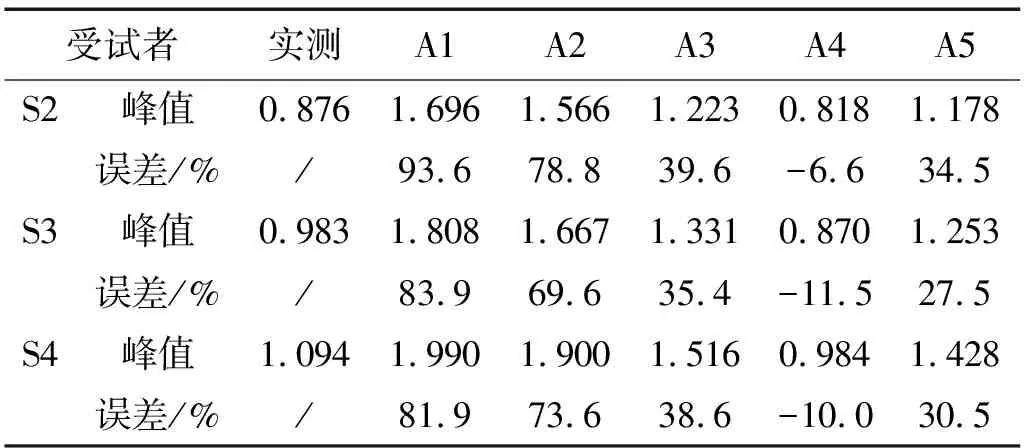
表5 實測與數值結果

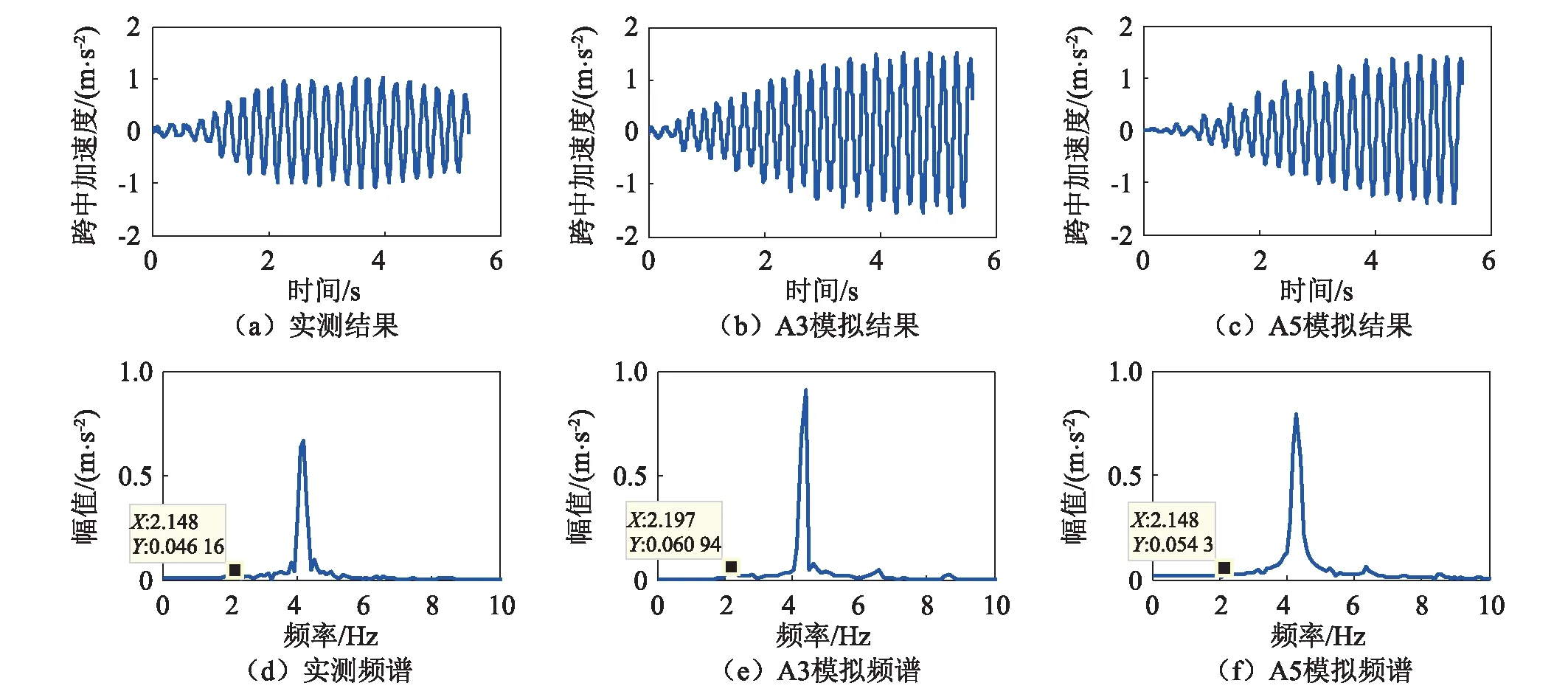
圖12 S4的模擬結果Fig.12 Simulation results of S4

4 結 論

對荷載模型A1～A5進行對比分析與實驗驗證工作，有以下結論：

(1)當結構基頻處于亞諧共振區時，需考慮亞諧分量的影響，其影響隨人/結構質量比的增加更顯著，忽略亞諧分量會導致計算結果偏小；處于倍頻共振區時，不考慮相互作用的移動力模型的計算結果與SMD模型相比顯著偏大，其共振響應預測結果偏于保守。

(2)ASMD模型Ⅱ既考慮了人-結構相互作用，又包含亞諧分量，能更好的預測結構人致響應，且較BWM模型更加簡化。