高原環境下爆炸沖擊波參數的有效預測方法
龐春橋, 陶 鋼, 周佩杰, 范 強, 劉 龍, 袁書強
(1.南京理工大學 能源與動力工程學院,南京 210094;2.重慶長安工業(集團)有限公司,重慶 401120;3.中國兵器工業集團第52研究所,浙江 寧波 315000)
超壓和正相比沖量是沖擊波對人員和結構等實現毀傷的主要參數[1]。在以往的研究中,平原地區的沖擊波研究已有很多[2-5],而高原環境對沖擊波參數影響的研究卻相對較少。文獻[6]給出了適合于不同海拔條件下的超壓預測公式,但是由于公式中涉及的試驗常數未知,因此很難直接應用。此外,經典的預測公式,一般為無限空間或半無限空間爆炸沖擊波參數計算,?而實際地面測試中一般存在炸高,當測試點處的沖擊波入射角大于其臨界角度時,測試結果會受到馬赫反射影響[7-10]。以上這些影響因素都必須認真考慮。
國內戰斗部爆炸沖擊波參數的試驗評估方法主要參考國軍標(GJB),其測試方法基本相同,但均存在不完善的問題,特別是高原環境對沖擊波正相比沖量的影響,現有GJB缺少相應的估算方法,所以在實際裝藥爆炸沖擊波參數的高原估算中,一直以來存在著理論和實踐脫節的問題。因此,迫切需要給出一種能夠用于高原條件下戰斗部爆炸沖擊波參數科學預測的方法,以便指導實際操作。
本文提出了一種能夠有效預測高原沖擊波參數的方法,并采用某試驗模擬彈分別在平原和海拔4 500 m的高原對爆炸產生的沖擊波參數進行了測試,驗證了該方法的高原適用性,同時給出了高原環境對沖擊波參數的影響。本研究可以為高原環境下沖擊波參數的預測評估,戰斗部爆炸威力的高原沖擊波性能指標確定提供參考。
1 預測模型
1.1 沖擊波超壓預測方法

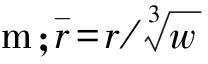
方程(1)是無界空間下的超壓計算公式,對于地面爆炸時,在一階近似下,正如在空氣中的爆炸情況,可以假設,爆炸能量不是分布在球體積中,而是在半球體積中。因此,奧爾連科提出對于在剛性表面爆炸,應按兩倍等效裝藥計算沖擊波參數。然而如果地面可變形或可壓縮,則有部分爆炸能量耗費于地面的變形以及在其中形成的沖擊波,所以在關于空氣沖擊波參數的公式中應當用等效裝藥質量表示,如we=2ηw,這里的系數η是考慮了爆炸能量耗散于空氣中的份額后得出的。對于絕對剛性地面,η=1。奧爾連科給出了不同介質表面爆炸時傳輸到空氣中的爆炸能量份額,其中混凝土,巖石等較堅硬介質的材料系數η=0.85~0.9。因此在本文中的情況下,可用we=1.8w修正式(3)。于是可得高原環境下沖擊波超壓公式:

(2)
式中:ΔpmGr為裝藥在較堅硬地面爆炸時的沖擊波峰值超壓,MPa。
方程(2)為不同海拔條件下地面爆炸時空氣沖擊波峰值超壓公式,實際地面測試過程中一般存在炸高,當測試點處的沖擊波入射角大于馬赫反射臨界角度時,測試結果會受到馬赫反射影響,此時壓力傳感器所測得的超壓值為馬赫桿壓力。為了使方程(2)的計算結果與試驗測試結果相匹配,需要將其換算為地面測試時的沖擊波超壓。換算關系式為[12-13]:
Δpm=ΔpmGr×(1+cosφ0)
(3)
式中:Δpm為地面傳感器測試得到的峰值超壓,MPa;φ0為實際測試時的沖擊波入射角。
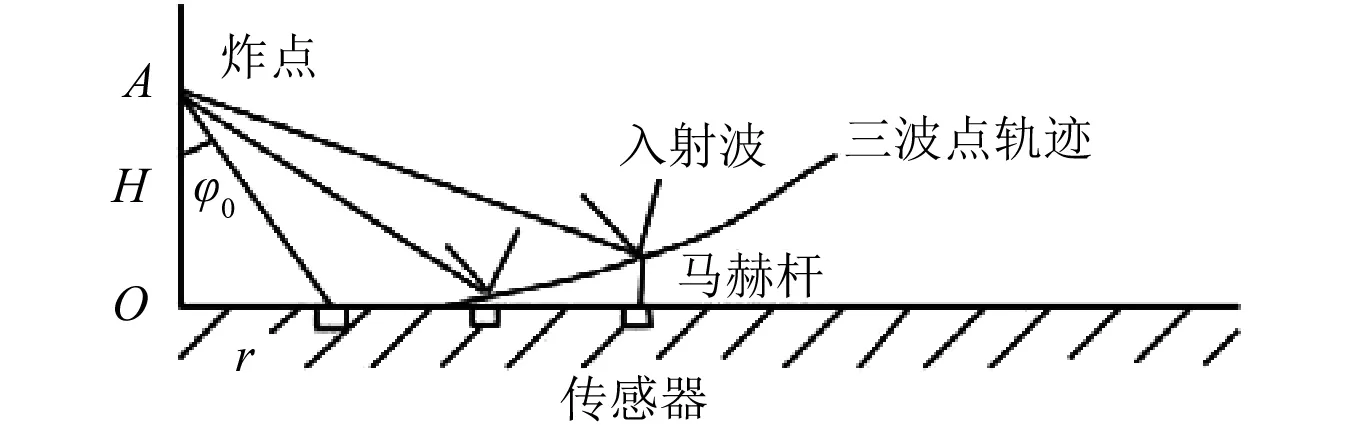
圖1 馬赫反射示意圖Fig.1 Schematic diagram of mach reflection
圖1給出了測試過程中沖擊波發生馬赫反射的示意圖,根據圖中的信息可以得到沖擊波入射角的計算公式為:
φ0=arctan(r/H)
(4)
式中:r為測試點到爆炸中心的距離,m;H為炸高,m。
1.2 沖擊波正相比沖量預測方法

(Im)h=λ(Im)0
(5)
式中:λ為海拔修正系數。當爆炸比例距離大于0.9 m/kg1/3時,λ=1-0.036 55h,h為海拔高度,km。通過該修正系數并結合表1中不同海拔條件下大氣壓力參數[15]便可以得到海拔修正系數與相應海拔高度處大氣壓力和海平面大氣壓力比值之間的對應關系。為了保持正相比沖量的海拔修正系數與薩多斯基高原超壓公式形式的相似性,擬采用方程(6)的形式對正相比沖量的海拔修正系數進行擬合,擬合得到A=0.32≈1/3,結果如圖2所示。
λ=(ph/p0)A
(6)

表1 不同海拔高度下的大氣壓力

圖2 正相比沖量海拔修正系數擬合Fig.2 The fitting curve of altitude coefficient for specific impulse

(7)
對方程(7)進行整理變換得的高原環境下沖擊波正相比沖量公式:
(8)
式中:i+Gr為裝藥在較堅硬地面爆炸時的沖擊波正相比沖量,Pa·s;ph為當地海拔高度下的大氣壓力,MPa;p0為海平面的大氣壓力,MPa。
與峰值超壓的預測方法相同,修正后的正相比沖量方程(7)為不同海拔條件下地面爆炸時空氣沖擊波正相比沖量公式,為了使方程(7)的計算結果與正相比沖量的試驗測試結果相匹配,需要將其換算為地面測試時的沖擊波正相比沖量。換算關系表達式為[16]:
i+=i+Gr×(1+cos2φ0),45°<φ0<90°
(9)
式中:i+為通過對測試數據進行積分得到的沖擊波正相比沖量。
2 試 驗
2.1 測試系統布置
為了驗證本文給出的預測模型的高原適用性,采用某試驗模擬彈分別在平原和高原進行靜爆試驗,試驗裝藥為圓柱形裝藥,裝藥量為3.5 kg,炸高為1.5 m。依據面殺傷戰斗部靜爆威力試驗方法[16]的要求,在平原(海拔高度200 m)地區進行的試驗中,超壓傳感器分別布置在距離爆炸中心3 m,5 m,7 m處,每個測試距離按東南西北布置4個傳感器。在高原(海拔高度4 500 m)地區進行的試驗中,超壓傳感器分別布置在距離爆炸中心2.7 m,4.8 m,6.3 m,7.2 m處,與平原試驗相同,每個測試距離按東南西北布置4個傳感器。其中,平原地區靜爆7發,高原地區靜爆5發。測試傳感器為KISTLER公司的211B5型壓電式石英傳感器,采用的是地面布置傳感器的方法。數據采集設備為DEWETRON公司的2010型數據采集儀。同時為了直觀的得到爆炸產生的火球大小,進而得到模擬彈爆炸時的近場區域尺寸,試驗中在爆炸中心西側120 m處布置高速錄像,對爆炸過程進行記錄。
2.2 沖擊波參數的判讀
每發試驗在各個測試距離上可獲得4條測試曲線,首先對測試曲線進行篩選,去除明顯不屬于沖擊波波形和測試量級明顯不合理的信號,然后對采集到的數據進行判讀,以得到沖擊波特征參數。沖擊波測試的典型曲線如圖3所示。通過該測試曲線可以得到沖擊波在該位置處的超壓,正壓作用時間和正相比沖量,其中正相比沖量由積分得到。

圖3 沖擊波參數Fig.3 Shock wave parameters
2.3 試驗可行性分析
不同裝藥形狀對爆炸沖擊波超壓與正相比沖量有一定的影響。本文中的預測模型是基于球形裝藥的,而試驗采用的是圓柱形裝藥結構,因此需要對試驗驗證的可行性進行分析。文獻[17]通過AUTODYN方法模擬了不同形狀裝藥爆炸的沖擊波場,結果表明圓柱形裝藥爆炸時具有明顯的方向性,其與等效球形裝藥爆炸的差異主要集中在圓柱形裝藥的軸向與徑向,而在兩位置的中間區域由于波的疊加與等效球形裝藥是基本一致的。本文中試驗測試點均位于該中間區域,因此可以用于對本文預測模型的驗證。
3 試驗結果與分析
3.1 試驗結果
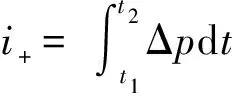
根據方程(4)可知,本文中平原地區入射角分別為63.4°,73.3°,77.9°,高原地區入射角分別為61.0°,72.6°,76.6°,78.2°。根據文獻[18]中查出的馬赫反射臨界角為40°可知,本文中所有測試點均位于馬赫反射區,因此試驗中壓力傳感器所測得的超壓值均為馬赫桿壓力,具體測試結果如表2,表3所示。
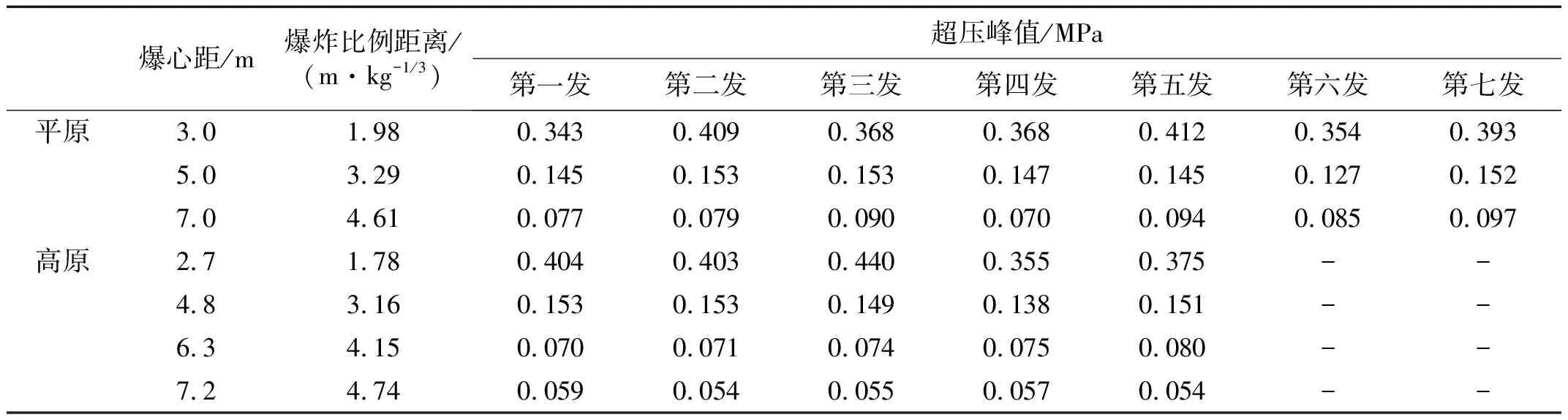
表2 沖擊波超壓
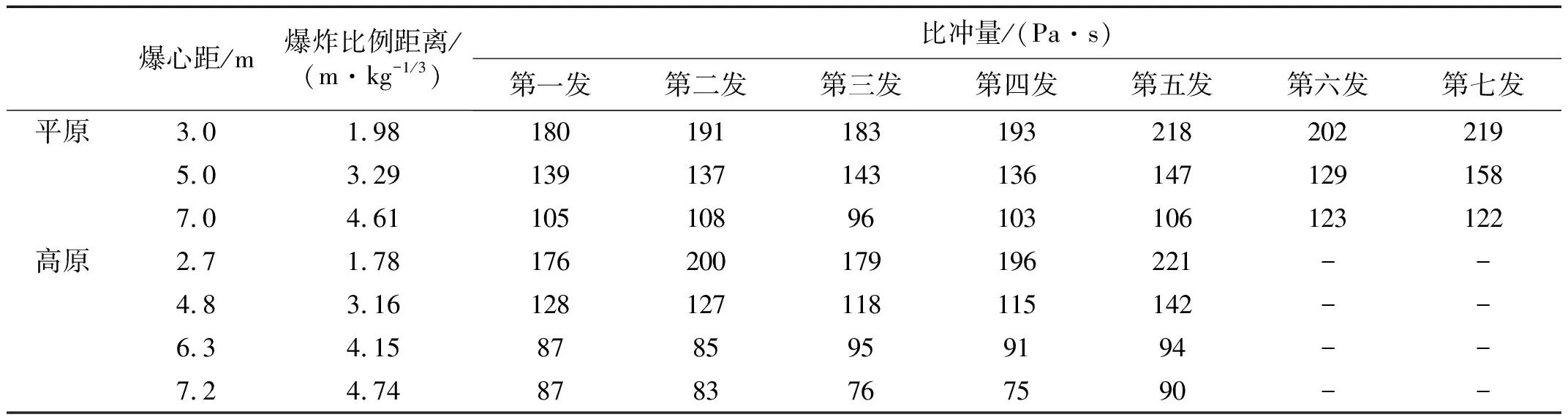
表3 沖擊波比沖量


圖4 爆炸場景Fig.4 The scene of explosion
3.2 分析與討論
應用文中給出的沖擊波峰值超壓預測方法分別計算平原和高原條件下沖擊波超壓隨爆炸比例距離變化的曲線并與試驗數據做了對比,如圖5,圖6所示。

圖5 預測公式計算超壓曲線與平原測試點的對比Fig.5 The comparison between the plain test point and the overpressure curve calculated by the predictive formula
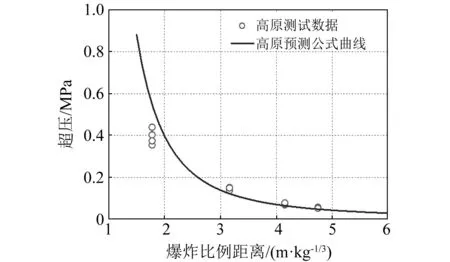
圖6 預測公式計算超壓曲線與高原測試點的對比Fig.6 The comparison between the plateau test point and the overpressure curve calculated by the predictive formula
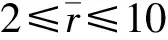
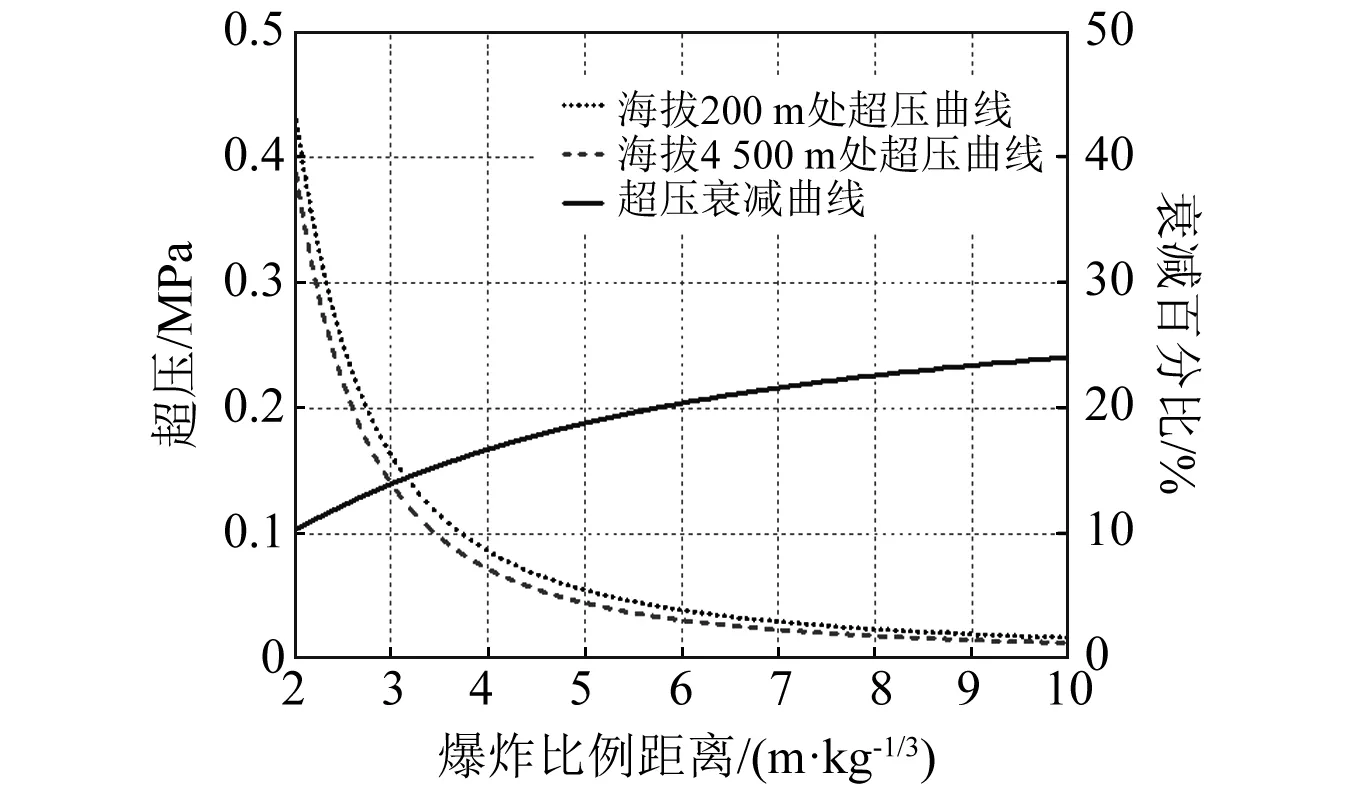
圖7 超壓衰減曲線Fig.7 The decay curve of overpressure
應用Ramezan Ali IZADIFARD等的數值模擬結果對奧爾連科的正相比沖量公式進行高原環境下的修正,并由此建立了沖擊波正相比沖量預測方法,應用該方法分別計算平原和高原條件下比沖量隨爆炸比例距離的變化關系并與試驗數據點進行對比,如圖8,圖9所示。
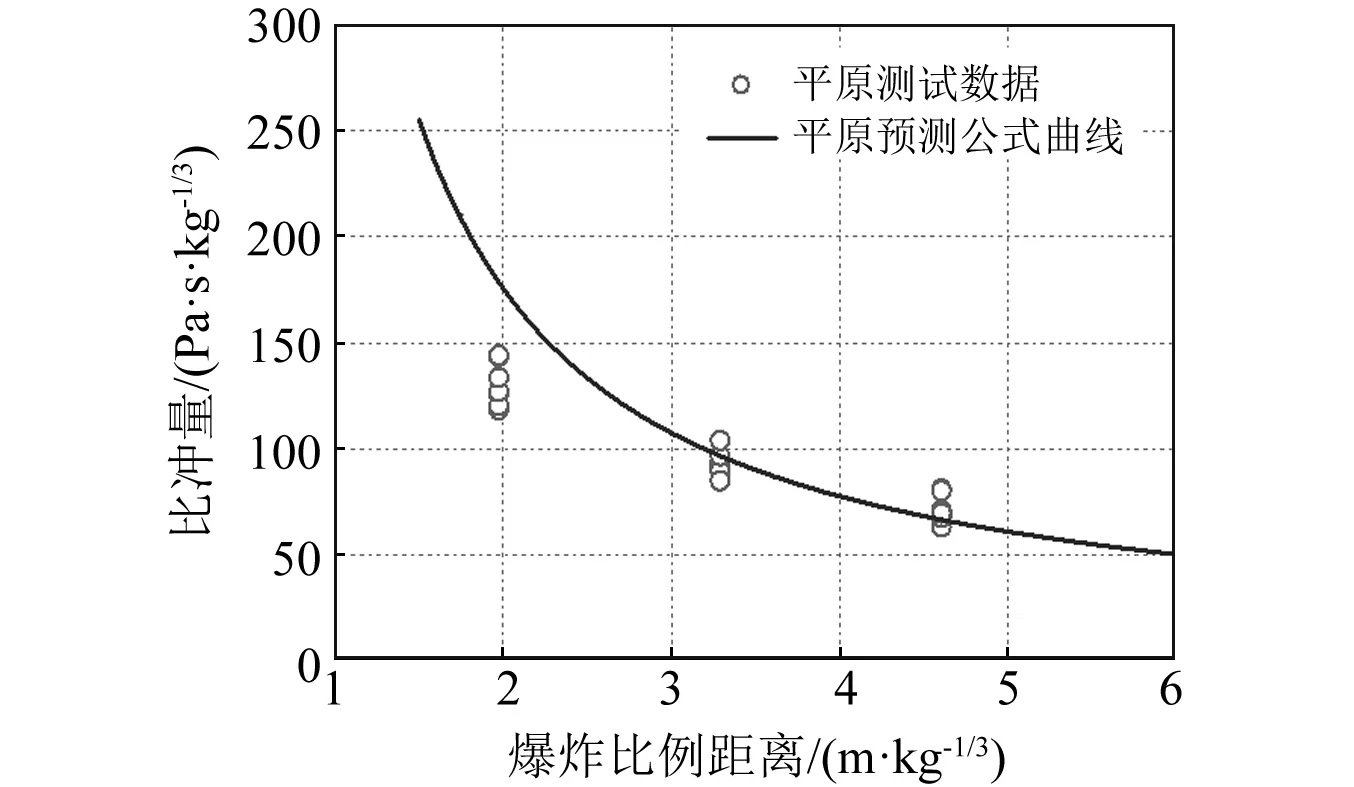
圖8 預測公式計算比沖量曲線與平原測試點的對比Fig.8 The comparison between the plain test point and the specific impulse curve calculated by the predictive formula
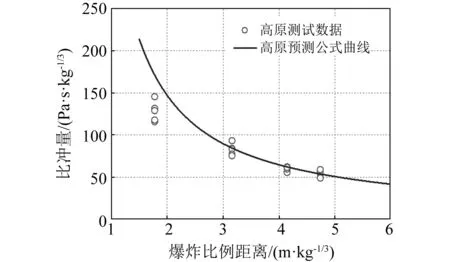
圖9 預測公式計算比沖量曲線與高原測試點的對比Fig.9 The comparison between the plateau test point and the specific impulse curve calculated by the predictive formula

海拔高度/m2004 500真實距離/m3572.74.86.37.2爆炸比例距離/(m·kg-1/3)1.983.294.611.783.164.154.74試驗平均值/ (Pa·s·kg-1/3)1981411091941269082計算值/ (Pa·s·kg-1/3)2701471022591299482計算誤差/%36.44.36.433.52.44.40.0

4 結 論
在前人研究基礎上提出了一種能夠有效預測高原沖擊波參數的方法,并通過模擬彈在平原和高原靜爆試驗對該方法進行了驗證,得到以下結論。
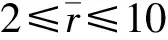
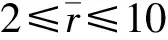
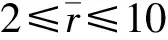
(4)沖擊波正相比沖量隨海拔高度的增加而降低。當海拔由200 m增加到4 500 m時,模擬彈爆炸產生的正相比沖量衰減在17%左右。
本文提出的高原環境下的沖擊波參數預測方法,不僅能夠計算高原沖擊波超壓及正相比沖量,還可以給出高原環境對沖擊波參數的影響規律。該方法可以為戰斗部高原沖擊波性能指標的確定以及國軍標的進一步完善提供有效參考。

