淺析破解初中數學幾何推理的思路

◎胡琴

前言：中學數學科目的新課標一直把幾何推理以及證明當作數學教學當中的重要內容，同時幾何推理有關問題也是中考一個必考題型，其考查知識十分全面，而且綜合性非常強，其能夠將代數知識和幾何知識進行有機結合，對數形結合這種思想進行逐漸滲透，重點在于對學生的邏輯思維以及分析能力進行考查。而其難點就是怎樣借助眾多定義以及定理確定證明思路。所以，激發學生的幾何學習興趣，幫其建立由內容逐漸到形式，由題設逐漸到結論的解題思路十分重要。

一、設置情景，調動學生的學習熱情及興趣

針對初中生而言，其對新知識都充滿一定興趣。因此，數學課上，教師需對生活實例加以運用，設置情景以及疑障，不斷鼓勵學生進行大膽猜測，調動其求知欲望。

例如，學習三角形全等的判定定理（ASA）時，引入：一塊玻璃，在打碎之后變成三塊，其中一塊僅保留一個角，另一塊保留兩個角，而中間一塊無完整的邊以及角，重新配時要帶哪一塊？

設置這一情景是為借助和生活有著密切聯系的實例活躍課堂氛圍，促使學生能夠更快進入到學習狀態。

實際上，情景教學非常重視情感，并且提倡著學以致用。因此，數學教學需把培養學生能力當作手段，在教學當中實踐性，將當前教學與今后應用進行結合，同時重點培養學生對知識的應用能力。

再如，講解相似三角形具體應用之時，教師可在課前對測量金字塔的高度這一典故進行講解。在古希臘，泰勒斯對金字塔的高度加以測量，在當時條件非常落后的情況之下，怎樣對塔高進行測量。此時教師可因勢利導的對相似三角形這一知識加以引入，在完成新課學習之后，回頭對泰勒斯的測量方法加以思考，這樣學生會有一種恍然大悟的感覺。通過一個持續性問題情境，能夠激發初中生思維，并且對運用所學知識的意識進行提高［1］。

二、動手實踐，提升學生對于幾何圖形具體感性認識

如今，新課標已明確指出了，通過幾何教學需對學生識圖、畫圖、幾何語言、符號轉換以及推理能力加以培養，進而為學生日后學習奠定基礎。動手操作能夠提升學生對于幾何圖形的認識。所以，教學期間，教師需對學生作圖能力的培養加以重視，同時通過語言表達加深初中生對基本圖形的理解。

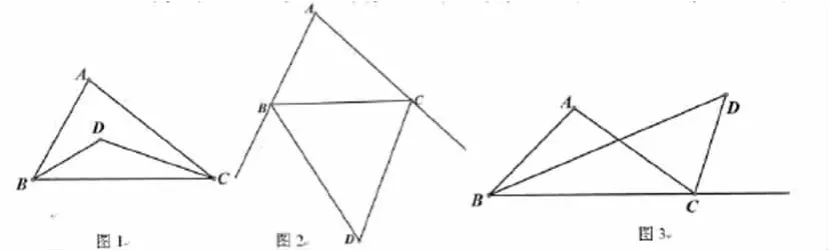
例如，△ABC之中，BD是∠ABC的角平分線，CD是∠ACB的角平分線，已知∠A＝50°，問∠CDB的度數.

對于此題，教師需先讓初中生根據題意把圖形畫出來，通常初中生很容易便會得到圖1。此時，教師可問學生：假設兩條內角的角平分線變成外角的角平分線，則其相交形成的角，怎樣求其度數？初中生可根據教師所問畫出圖2。此時，教師可再進行提問，假設一個內角的角平分線與一個外角角平分線相交，則又會有怎樣的情況？初中生可按照題意畫出圖3.這樣一來，可讓初中生通過動手實踐逐漸提高對于幾何圖形的認識［2］。

三、訓練學生幾何語言，不斷培養其推理能力

其實，幾何概念以及幾何語言都是對題目進行理解，轉化圖形的一種語言，是進行邏輯推理的重要前提。第一，教師需讓初中生學會對幾何命題當中題設以及結論進行劃分的方法。在一個命題之中，題設屬于已知條件，也就是被判斷的具體對象，而結論是根據已知條件通過判斷得到的結果，即求證部分。教學期間，教師需在日常訓練當中強化學生對于幾何命題的具體理解。第二，培養學生把文字命題轉變成幾何語言，同時畫出相應圖形的這種能力［3］。其主要步驟為：按照命題題意把相應幾何圖形畫出來，同時借助字母進行標注。之后按照題意，同時結合圖形，把題設及結論借助數學符號以及數學算式進行具體化。

例如，證明：角平分線上的點到角的兩邊距離是相等的。

已知：畫出相應圖形，如圖OC為∠AOB角平分線，P是OC之上的一點，且有OA⊥PD，OB⊥PE，且垂足分別是點D和點E.

證明：PE＝PD.

針對初中生而言，數學教師需注意強化其對于幾何符號這種語言的訓練以及培養。

結論：綜上可知，對初中生的幾何方面邏輯推理這一能力加以培養不是短時間內就能完成的，其需要教師以及學生一同進行努力。初中生需在教師具體引導之下，對典型例題具體解題步驟加以思考，同時在大腦當中對解題思維具體框架進行構架。此外，教師也需引導學生積極進行歸納整理。在教學期間，關注定義、定理以及性質方面結論，為學生提供相應變式訓練，及時對學生加以指導，這樣才能促使學生幾何方面的邏輯推理這一能力漸漸得到提升。