基于微極理論的新型FeAl多孔材料彈性模量研究

蘇淑蘭，饒秋華，賀躍輝，張惠斌

?

基于微極理論的新型FeAl多孔材料彈性模量研究

蘇淑蘭1, 2，饒秋華2，賀躍輝3，張惠斌3

(1.中南林業(yè)科技大學 土木工程學院，湖南 長沙，410004；2. 中南大學 土木工程學院，湖南 長沙，410075；3. 中南大學 粉末冶金研究院，湖南 長沙，410083)

針對本課題組制備的一種新型金屬間化合物多孔材料即FeAl多孔材料，分析其孔隙結構的微觀特征，建立六邊形多孔結構模型，利用微極理論和能量法推導出多孔材料彈性模量的理論計算公式，并通過單軸拉伸實驗加以驗證。研究結果表明：多孔材料的相對彈性模量1/s隨相對密度*/s增加而增大，且彎曲剪力對1/s的影響也隨之增大，故中、高密度的多孔材料必須考慮彎曲剪力對1/s的影響；采用能量法精確計算微極彈性連續(xù)介質的結構位移，且考慮彎曲剪力對相對彈性模量的影響，理論公式計算的彈性模量更接近于實驗結果，從而驗證了彈性模量理論公式更加準確、可靠。

FeAl金屬間化合物多孔材料；彈性模量；微極理論；能量法；單軸拉伸實驗

金屬多孔材料具有很多比致密材料更優(yōu)的特性，如比表面積大、比力學性能好、吸附容量大等，作為一種功能和結構材料，已廣泛應用于航空、機械、建筑、冶金、醫(yī)藥、生物、化工等領域[1?5]。本課題組[6]提出元素混合粉偏擴散—反應合成—燒結方法，制備出一種新型的金屬間化合物多孔材料，即FeAl多孔材料，與金屬多孔材料相比，它具有優(yōu)良的高溫抗氧化和抗腐蝕性能、較高的比強度和比模量、易加工成形和可焊接連接等優(yōu)點，工程應用前景十分廣闊[7?9]。目前，已制備一種新型的具有階梯孔梯度的FeAl多孔材料均質過濾膜[10]，可用于高溫和惡劣(如強腐蝕或硫化)環(huán)境下的過濾、分離、凈化和提取等工藝過程。作為一種新的金屬間化合物多孔材料，FeAl多孔材料的研究尚處于起步階段[6, 11?13]，其力學性能是保證材料應用于工程實際的重要指標。目前，多孔材料的力學性能研究多數采用模型分析方法，如幾何模型[14?15]、復合材料力學模型[16?17]以及基于高階連續(xù)介質理論[18?19]的微極理論模型[20?22]等，其中微極理論應用較廣。通過微極理論推導多孔材料彈性模量的理論計算公式時，確定結構位移至關重要，一般是利用幾何變形關系來近似計算，且忽略彎曲剪力的影響，缺乏足夠的計算精度。本文作者基于FeAl多孔材料的孔隙結構微觀特征分析，建立該材料的六邊形多孔結構模型，利用微極理論和能量法，推導FeAl多孔材料彈性模量的理論計算公式，并通過單軸拉伸實驗加以驗證，以便為新型FeAl多孔材料的優(yōu)化設計和應用推廣提供重要的理論依據。

1 多孔結構模型

圖1所示為FeAl金屬間化合物多孔材料孔隙結構的SEM照片[5]。由圖1可知：FeAl多孔材料的孔隙分布比較均勻，可將其抽象為圖2所示的六邊形多孔結構模型。將六邊形多孔結構看成是彈性梁(,和)，在梁的端點處通過結點()互相連接而成。選取圖3中△123圍成的三角形部分為代表單元體，1，2和3為相鄰3個六邊形的中心。

圖1 FeAl多孔材料的微觀結構形貌

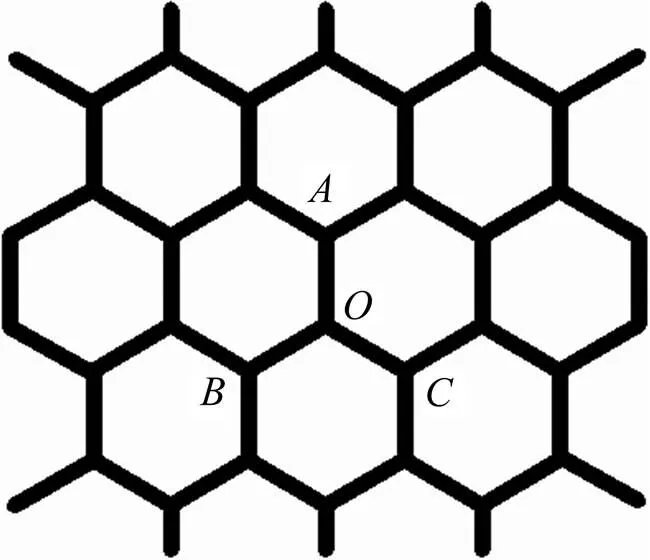
圖2 六邊形多孔結構

2 多孔材料彈性模量推導

為了推導出多孔材料的彈性模量，將多孔材料均勻化成微極彈性連續(xù)介質，由應變能等效原理求得微極彈性連續(xù)介質的微極剛度系數和微極彈性常數，再利用微極理論推導出多孔材料宏觀彈性模量的理論計算公式。

2.1 微極理論基本方程

在ERINGEN[18]的微極理論中，假設材料中的任一微元體都是由許多連續(xù)可變形的物質點構成，每一個物質點具有6個自由度(3個平動自由度和3個轉動自由度)，即物質點不但能夠傳遞力，而且能夠傳遞力矩。微極理論的基本方程如下。

平衡方程：

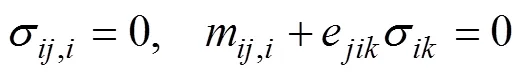
本構方程：

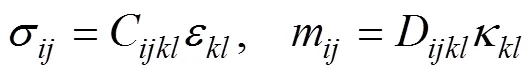
幾何方程：

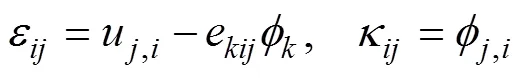
其中：σ和ε分別為應力和應變張量；m和κ分別為偶應力和扭率張量；C和D為線彈性微極理論中的剛度系數張量；u和φ分別為物質點的平動和轉動位移；e為三階置換張量。

對于各向同性、中心對稱的微極介質，其剛度系數張量C和D可以用2個拉梅常數(和)和4個微極彈性常數(，，和)表示為[23]

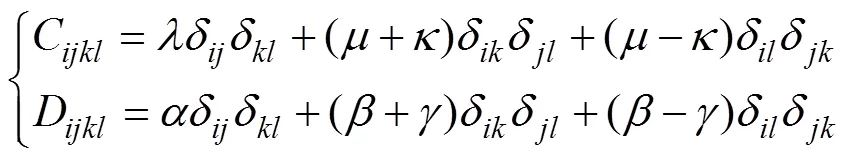
其中：δ為Kroneker Delta符號。

將式(4)代入式(2)可得應力張量σ和偶應力張量m分別為

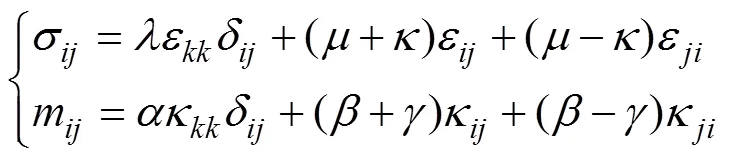
2.2 微極剛度系數和微極彈性常數

采用能量法精確計算微極彈性連續(xù)介質的變形，進而求得微極剛度系數和微極彈性常數。

將圖3中的代表單元體均勻化成等效的微極彈性連續(xù)介質，由應變能等效可知，代表單元體的應變能cell(即單元體內各彈性梁的應變能之和)等于均勻化后微極彈性連續(xù)介質的應變能con，即

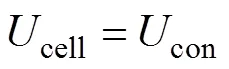
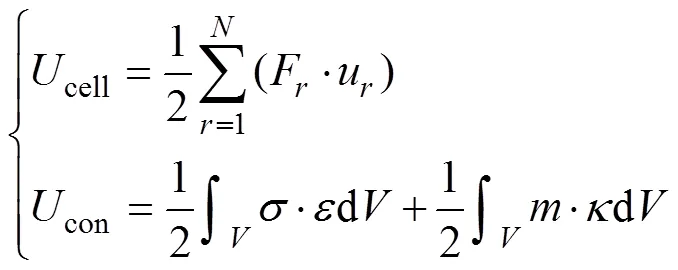
其中：為與結點相連的彈性梁總數；F和u分別為第根彈性梁所受的廣義荷載和廣義位移；和分別為應力和應變；和分別為偶應力和扭率；為單元體體積。

多孔結構受荷載作用時，將彈性梁看成兩端固支(因梁的兩端與結點相連)，則彈性梁橫截面上的內力有軸力、剪力和彎矩。且設彈性梁的位移分別為1()，2()和()，則相應的應變ε和曲率κ可由幾何方程(即式(3))得到，由此可得第根彈性梁沿軸線方向的平均應變(r)、沿法線方向的平均應變(r)及平均曲率(r)分別為

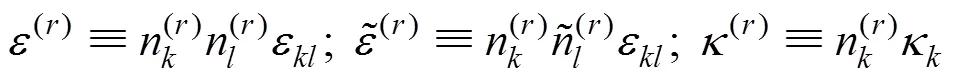
再根據梁理論中力?位移、力矩?轉角關系，梁的內力可表示為

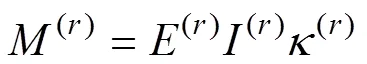
其中：(r)為第根彈性梁的彈性模量；(r)，(r)和(r)分別為第根彈性梁的長度、橫截面面積和慣性矩；(r)為1個彎曲剛度與剪切剛度之比的量綱一系數，(r)=0 表示彈性梁的剪切剛度很大，可以忽略彎曲剪切；(r)≥1，表示彈性梁的剪切剛度較小，必須考慮彎曲剪切產生的變形。

將式(8)和式(9)代入式(7)，可得代表單元體的應變能為

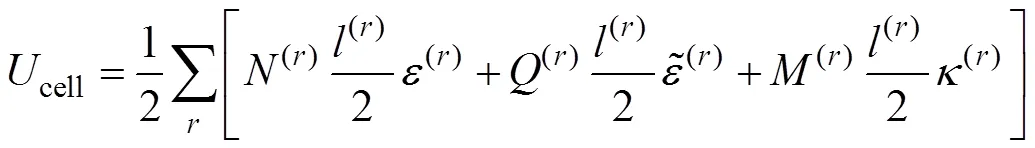
此外，將式(2)代入式(7)，可得均勻化后微極連續(xù)介質的應變能為

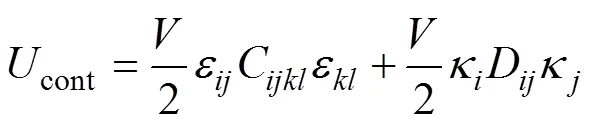
利用式(6)，由式(9)，(10)和(11)得到均勻化后微極連續(xù)介質的剛度系數張量為

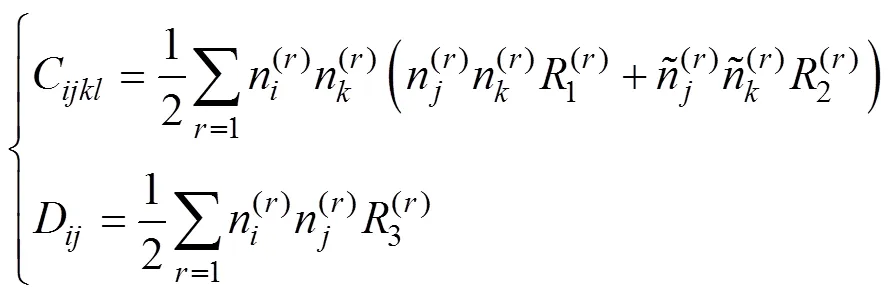
其中：

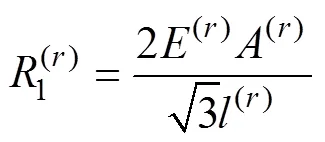
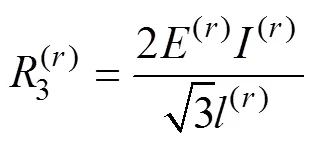
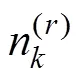
表1 單位矢量沿第r根彈性梁的軸向和法向分量

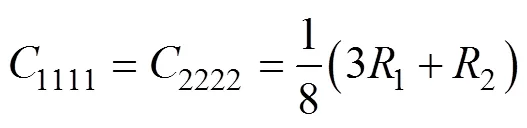
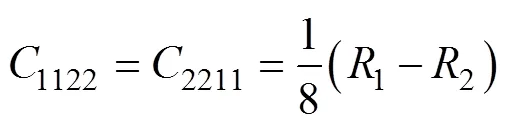
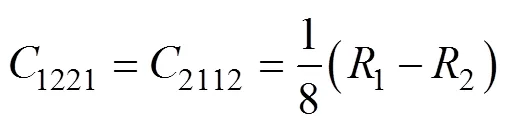
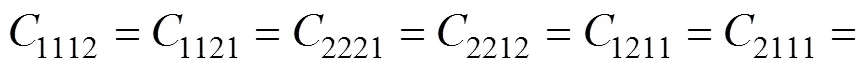
由式(13)可將微極剛度系數寫成以下統一形式：

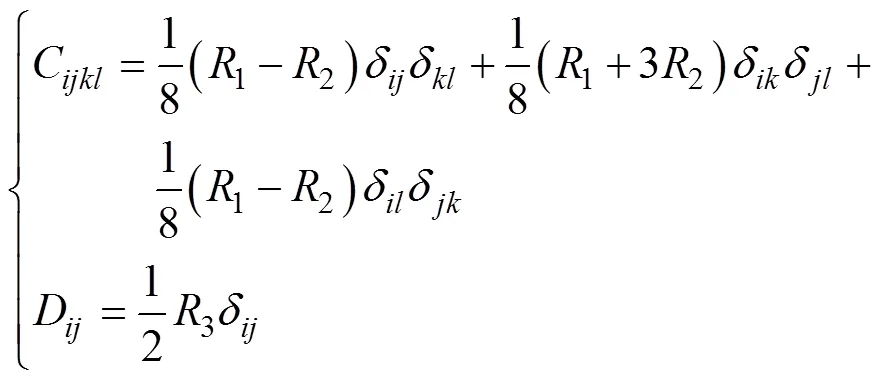
將式(15)與式(4)比較，可得微極連續(xù)介質的6個微極彈性常數分別為

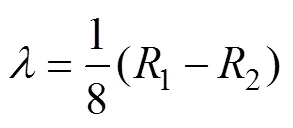
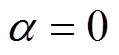
2.3 多孔材料的相對彈性模量

為了求得正六邊形多孔材料在1方向上的宏觀彈性模量1，考慮單位厚度的微極連續(xù)介質在1方向上作用均布應力11，且介質內產生的應力為1110，22=33=0，應變?yōu)?i>1110,22=33,12=23=13=0，則式(5)可以改寫為

注意到22=0，則有

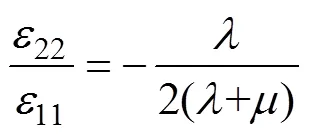
由式(17)和式(18)可得等效微極連續(xù)介質在1方向上的彈性模量1為

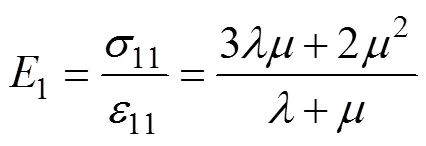
設圖3中的彈性梁是寬為、厚為的矩形截面，則橫截面面積、慣性矩分別為

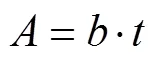
相對密度[3]為

式中：*和s分別為多孔材料和致密材料的密度。

單位厚度(=1)等效微極連續(xù)介質(各向同性)的拉梅常數和可由式(13)，(16)和(20)得到：

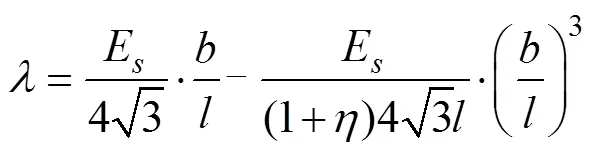
將式(21)和(22)代入式(19)，整理后得到1方向上的相對彈性模量1/s與相對密度*/s的顯式表達 式為

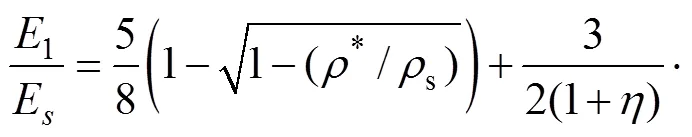
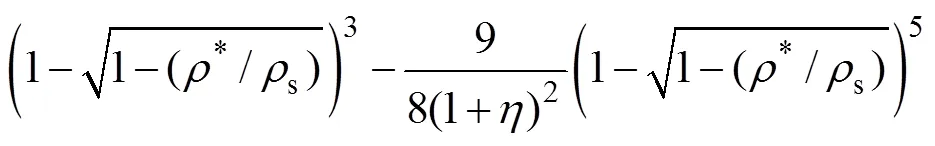
式中：s為致密材料的彈性模量；為彎曲和剪切剛度之比的量綱一系數(≥1)。

現有文獻中，基于復合材料力學理論[16]和微極理論[20]得到的多孔材料彈性模量理論公式分別為：

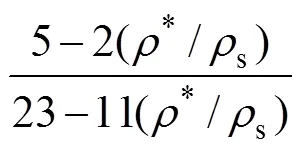
3 計算結果分析

3.1 ρ*/ρs對E1/Es的影響

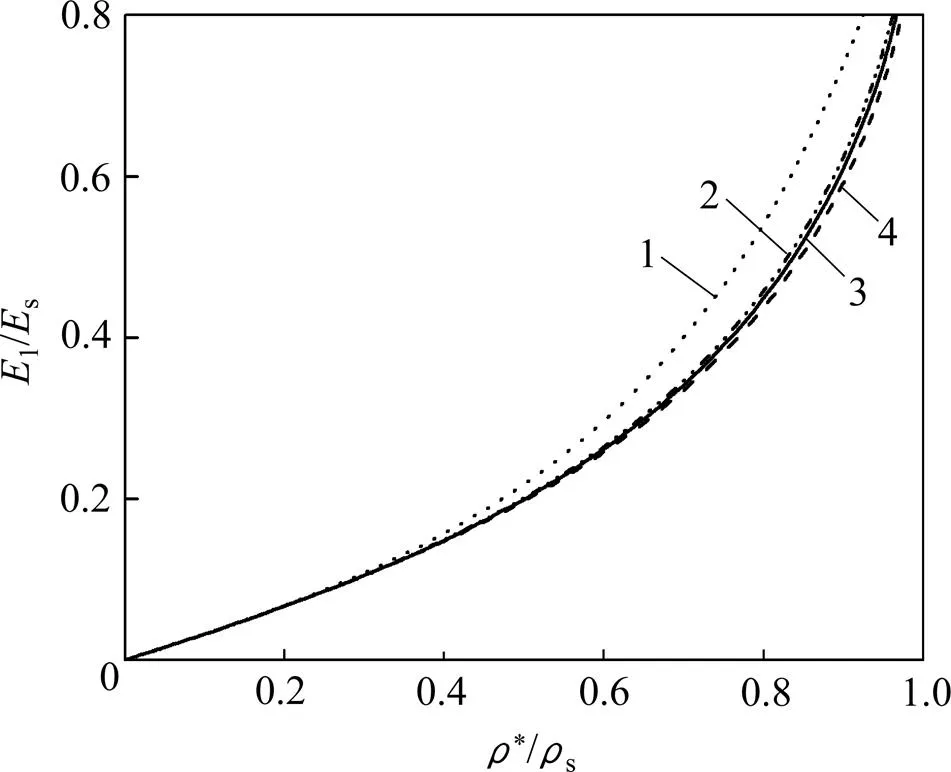
圖4所示為文獻[16]、文獻[20]和本文的相對彈性模量1/E隨相對密度*/ρ的變化結果。從圖4可見：相對彈性模量1/E隨相對密度*/ρ的增大而增大，這是因為相對密度增大即單位體積內固體材料增加，多孔材料抵抗彈性變形的能力也隨之增大，該結論與實際情況相符。

文獻[16]采用復合材料力學理論，將多孔材料看成是由致密體與孔隙2種材料組成，把孔隙的彈性模量取值為0，當相對密度較高時，從根本上無法考慮孔隙的分布及孔隙之間的相互作用對彈性模量的弱化。本文和文獻[20]都考慮了材料的微結構特征，將其均勻化成微極彈性連續(xù)介質，但文獻[20]是通過幾何變形關系近似計算得到的結點位移和轉角，而本文是通過能量法精確計算得到微極介質位移，同時還考慮了彎曲剪力對相對彈性模量的影響，故采用本文的理論公式計算FeAl多孔材料的彈性模量更為準確、可靠。

1—文獻[16]中結果；2—文獻[20]中結果；3—本文結果(η=1.2)。

3.2 彎曲剪力對E1/Es的影響

圖5所示為=0(忽略剪力的影響)和≥1(考慮剪力影響) 2種情況下彎曲剪力對1/s的影響。從圖5可見：在低密度范圍內，不同的1/s幾乎是重合的，這是因為當相對密度很小時，可將彈性梁簡化為Bernoulli-Euler梁(=0)，彎曲剪力所產生的變形很小，可以忽略剪力的影響；在中、高密度范圍內，彈性梁為Timoshenko梁(≥1)，彎曲剪力所產生的變形不能忽略，故相對密度較大時必須考慮剪力的影響，且相對密度越大，剪力影響(=0和≥1)越大，該結論與現有文獻[22]中一致。顯然，考慮彎曲剪切變形的1/s要遠低于忽略剪力時的1/s，更偏于安全。

η：1—0；2—1.0；3—1.2；4—1.5。

4 實驗驗證

4.1 拉伸實驗方案

采用本課題組制備的FeAl多孔材料和致密材料進行單軸拉伸實驗，通過阿基米德法測得FeAl多孔材料的孔隙率為10.9%，相對密度為0.891，為高密度多孔材料。

按照GB/T 228—2010，將拉伸試件設計成矩形截面的比例試樣，橫截面長×寬為2 mm×3 mm(見圖6)，通過線切割加工而成。實驗前將試件進行打磨拋光，且使試件充分暴露在大氣環(huán)境中24 h以上。

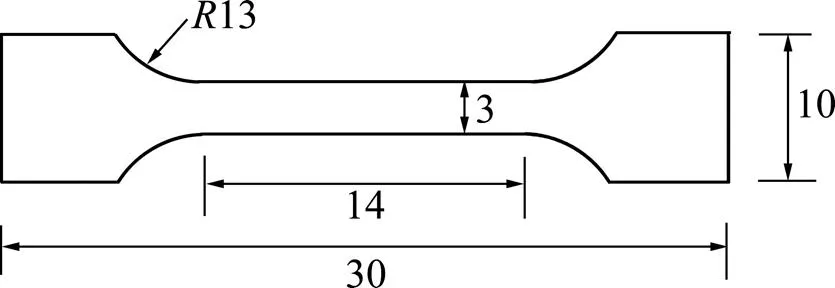
數據單位：mm

由于拉伸試件的尺寸太小，常規(guī)的萬能試驗機無法測定其準確應變，故采用MTS Insight生物力學試驗機，最大荷載為30 kN。將拉伸試件夾持在試驗機上且對中軸線，嚴格保持試件受軸向拉力作用。采用0.5 mm/min的加載速率對試件施加外載直至破壞，試驗機自動記錄相應的載荷與變形，以此繪制該試件的拉伸應力?應變曲線。

4.2 實驗結果分析

圖7所示為FeAl多孔材料和致密材料的拉伸應力?應變曲線。從圖7可見：2條曲線具有相同的變化規(guī)律，即均由彈性、屈服、強化和破壞等4個階段組成，但FeAl多孔材料的拉伸力學性能參數(如彈性模量、屈服極限和抗拉強度)均比FeAl致密材料的小。通過對應力?應變曲線的彈性段進行線性擬合，得到FeAl多孔材料的彈性模量1′、致密材料的彈性模量E分別為22.6 GPa和39.1 GPa。

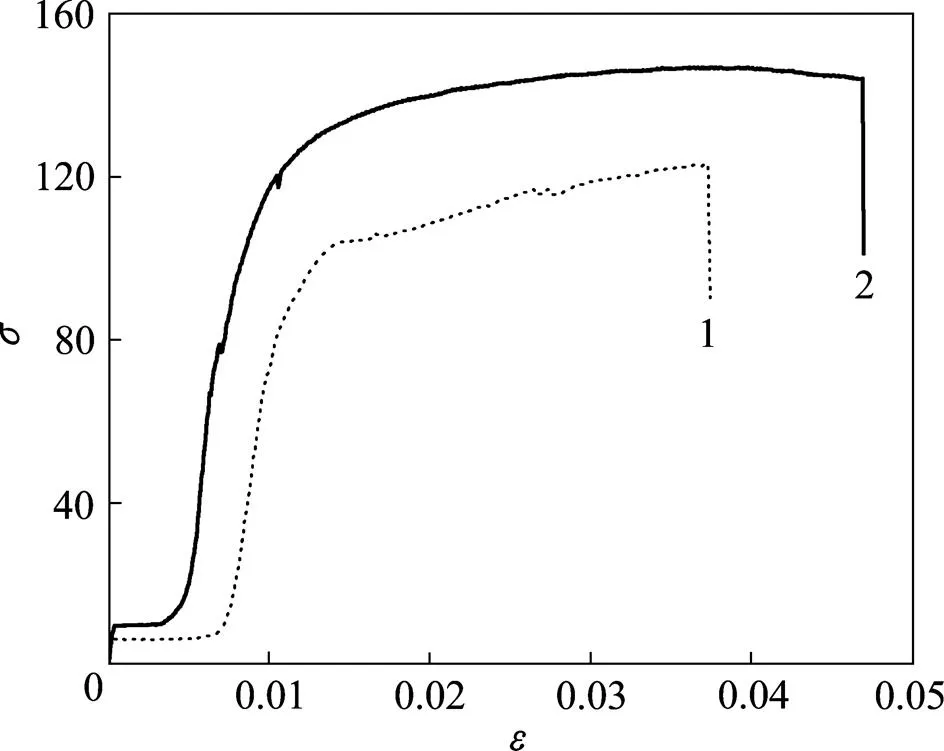
1—FeAl多孔；2—FeAl致密。

通過式(24)，(25)和(23)，可得到文獻[16]、文獻[20]和本文推導的FeAl多孔材料彈性模量理論值1，如表2所示。從表2可見：所有理論值1均高于實驗值1′，這是由于理論模型沒有考慮實際孔隙的非均勻分布。本文模型不僅采用能量法精確計算了微極彈性連續(xù)介質的位移，而且同時考慮了彎曲剪力對相對彈性模量的影響，故本文理論公式計算的彈性模量值更接近于實驗結果，從而驗證了本文推導的FeAl多孔材料彈性模量的理論公式準確、可靠。

表2 FeAl多孔材料的彈性模量

5 結論

1) 與現有的彈性模量理論計算公式相比，本文利用微極理論并采用能量法精確計算微極彈性連續(xù)介質的結構位移，且考慮了彎曲剪力對相對彈性模量的影響，故本文建立的彈性模量理論公式更為準確、可靠。

2) 隨著多孔材料的相對密度*/s增加，其相對彈性模量1/s隨之增大，且彎曲剪力對1/s的影響也隨之增大，故對于中、高密度多孔材料必須考慮彎曲剪力對彈性模量的影響。

3) 通過比較FeAl多孔材料彈性模量的實驗值與現有彈性模量計算公式的理論值，本文理論公式計算的彈性模量值更接近于實驗值，從而驗證了本文彈性模量理論公式的正確性。

[1] YAMAGUCHI A, UEJO F, YODA T, et al. Self-assembly of a silica-surfactant nanocomposite in a porous alumina membrane[J]. Nature Materials, 2004, 3(5): 337?341.

[2] 何曉宇, 劉詠, 李為, 等. 采用混合元素法制備多孔Ni3Al材料[J]. 中南大學學報(自然科學版), 2009, 40(2): 357?361. HE Xiaoyu, LIU Yong, LI Wei, et al.Preparation of porous Ni3Al material by blend element[J]. Journal of Central South University (Science and Technology), 2009, 40(2): 357?361.

[3] GIBSON L J, ASHBY M F. Cellular solids: Structure and properties-second edition[M]. Cambridge: Cambridge University Press, 1997: 1?9.

[4] LANG Fengqun, YU Zhiming, GEDEVANISHVILI S, et al. Corrosion behavior of Fe-40Al sheet in N2-11.2O2-7.5CO2atmospheres with various SO2contents at 1 273 K[J]. Intermetallics, 2003, 11(2): 135?141.

[5] 王輝, 周向陽, 李昌林, 等. 真空燒結制備三維通孔不銹鋼泡沫材料[J]. 中南大學學報(自然科學版), 2011, 42(8): 2178?2183.WANG Hui, ZHOU Xiangyang, LI Changlin, et al.Vacuum sintering of stainless steel foam with 3-D open-cell network structure[J]. Journal of Central South University (Science and Technology), 2011, 42(8): 2178?2183.

[6] 高海燕. Fe-Al金屬間化合物多孔材料的研究[D]. 長沙: 中南大學粉末冶金研究院, 2009: 37?47. GAO Haiyan. Investigation on Fe-Al intermetallic compound porous material[D]. Changsha: Central South University. Powder Metallurgy Research Institute, 2009: 37?47.

[7] 沈培智, 高麟, 高海燕, 等. FeAl金屬間化合物多孔材料高溫硫化性能及應用[J]. 粉末冶金材料科學與工程, 2010, 15(1): 38?43. SHEN Peizhi, GAO Ling, GAO Haiyan,et al. High-temperature sulfidation behavior and application in SO2-containing gas cleanup of porous FeAl intermetallics[J]. Materials Science and Engineering of Powder Metallurgy, 2010, 15(1): 38?43.

[8] 高海燕, 賀躍輝, 沈培智, 等. FeAl多孔材料與不銹鋼的焊接[J]. 中國有色金屬學報, 2009, 19(1): 90?95. GAO Haiyan, HE Yuehui, SHEN Peizhi,et al. Welding of FeAl porous material and stainless steel[J]. The Chinese Journal of Nonferrous Metals, 2009, 19(1): 90?95.

[9] GAO Haiyan, HE Yuehui, ZOU Jin, et al. Pore structure control for porous FeAl intermetallics[J]. Intermetallics, 2013, 32: 423?428.

[10] 賀躍輝, 江垚, 高海燕, 等. 一種制備孔徑梯度FeAl金屬間化合物均質過濾膜的方法: 中國, 200710035404.4[P]. 2008?01?23. HE Yuehui, JIANG Yao, GAO Haiyan, et al. A preparation method of pore gradient homogeneous FeAl filter membrane: China, 200710035404.4[P]. 2008?01?23.

[11] SU Shulan, RAO Qiuhua, HE Yuehui. Theoretical prediction of effective elastic constants for new intermetallic compound porous material[J]. Transactions of Nonferrous Metals Society of China, 2013, 23(4): 1090?1097.

[12] 王杰豐, 高海燕, 江垚, 等. 造孔劑(NH4)2CO3含量對FeAl多孔材料性能的影響[J]. 粉末冶金材料科學與工程, 2014, 19(4): 654?658.WANG Jiefeng, GAO Haiyan, JIANG Yao,et al. Effect of pore-forming agent (NH4)2CO3content on properties of porous FeAl materials[J]. Materials Science and Engineering of Powder Metallurgy, 2014, 19(4): 654?658.

[13] 朱勝利, 張惠斌, 江垚, 等. 添加Cr合金化FeAl金屬間化合物多孔材料的制備及性能[J]. 粉末冶金材料科學與工程, 2016, 21(3): 427?433. ZHU Shengli, ZHANG Huibin, JIANG Yao,et al. Preparation and properties of porous FeAl intermetallics with Cr ternary additions[J]. Materials Science and Engineering of Powder Metallurgy, 2016, 21(3): 427?433.

[14] LI K, GAO X L, ROY A K. Micromechanics model for three-dimensional open-cell foams using a tetrakaidecahedral unit cell and Castigliano’s second theorem[J]. Composites Science and Technology, 2003, 63(12): 1769?1781.

[15] CHUANG C H, HUANG J S. Elastic moduli and plastic collapse strength of hexagonal honeycombs with plateau borders[J]. International Journal of Mechanical Sciences, 2002, 44(9): 1827?1844.

[16] 盧子興, 黃筑平, 王仁. 聚氨酯泡沫塑料壓縮楊氏模量的理論預測[J]. 應用力學學報, 1996, 13(2): 9?12. LU Zixing, HUANG Zhuping, WANG Ren. The theoretical prediction of compressive Young’s moduli for polyurethane foam plastics[J]. Chinese Journal of Applied Mechanics, 1996, 13(2): 9?12.

[17] RAMAKRISHNAN N, ARUNACHALAM V S. Effective elastic moduli of porous solids[J]. Journal of Material Science, 1990, 25(9): 3930?3937.

[18] ERINGEN A C. Microcontinuum field theory[M]. New York: Springer, 1999: 101?248.

[19] 胡更開, 劉曉寧, 荀飛. 非均勻微極介質的有效性質分析[J]. 力學進展, 2004, 34(2): 195?214.HU Gengkai, LIU Xiaoxun, XUN Fei. Micromechanics of heterogeneous micropolar mediums[J]. Advances in Mechanics, 2004, 34(2): 195?214.

[20] WANG X L, STRONGE W J. Micropolar theory for two-dimensional stresses in elastic honeycomb[J]. Proc Roy Soc Lond, 1999, A455: 2091?2116.

[21] OSTOJIA-STARZEWSKI M. Lattice models in micromechanics[J]. Applied Mechanics Review, 2002, 55(1): 35?60.

[22] KUMAR R S, MCDOWELL D L. Generalized continuum modeling of 2-D periodic cellular solids[J]. International Journal of Solids and Structures, 2004, 41(26): 7399?7422.

[23] NOWACHI W. Theory of asymmetric elasticity[M]. Oxford: Pergamon Press/Warsaw: PWN-Polish Scientific Publishers, 1986: 135?161.

Elastic modulus for new FeAl porous material based on micropolar theory

SU Shulan1, 2, RAO Qiuhua2, HE Yuehui3, ZHANG Huibin3

(1. School of Civil Engineering, Central South University of Forestry & Technology, Changsha 410004, China;2. School of Civil Engineering, Central South University, Changsha 410075, China;3. Powder Metallurgy Research Institute, Central South University, Changsha 410083, China)

A new type of intermetallic porous material, FeAl porous material, was prepared by our research group. A hexagonal pore structure model was established by analyzing its pore microstructure characteristics and a new calculation formula of elastic modulus was derived by micropolar theory and energy method for FeAl porous, and moreover, the calculation formula was verified by uniaxial tensile test. The results show that the relative elastic modulus1/sincreases with the increase of the relative density*/s, and the effect of bending shear force on1/salso increases, so the shear force must be considered for the medium and high density porous material. The energy method is adopted to calculate exactly displacements of micropolar elastic continuum and the effect of bending shear force on elastic modulus is considered, and therefore, the theoretical value of elastic modulus in this study is closer to its experimental value and more accurate and reliable.

FeAl intermetallic porous material; elastic modulus; micropolar theory; energy method; uniaxial tensile test

10.11817/j.issn.1672-7207.2018.07.010

TB383

A

1672?7207(2018)07?1643?07

2017?07?02；

2017?10?28

國家自然科學基金資助項目(11502307)；湖南省自然科學基金資助項目(2016JJ3187)；湖南省教育廳一般項目(14C1189)；中南林業(yè)科技大學引進高層次人才科研啟動基金資助項目(2014年) (Project(11502307) supported by the National Natural Science Foundation of China; Project(2016JJ3187) supported by the Natural Science Foundation of Hunan Province; Project(14C1189) supported by Education Department of Hunan Province; Project(2014) supported by the High-level Talents Scientific Research Starting Funds of Central South University of Forestry & Technology)

饒秋華，博士，教授，從事固體力學研究；E-mail: raoqh@csu.edu.cn

(編輯 楊幼平)