基于曲面擬合的復雜自由曲面網格劃分

陳禮杰，吳慧，李鐵瑞，高博青

?

基于曲面擬合的復雜自由曲面網格劃分

陳禮杰1，吳慧2，李鐵瑞1，高博青1

(1. 浙江大學 建筑工程學院，浙江 杭州，310058；2. 浙江財經大學 公共管理學院，浙江 杭州，310018)

為了實現復雜自由曲面的建筑網格劃分，將復雜自由曲面擬合成1個曲面，并利用映射法進行網格劃分。首先提出基于非均勻有理B樣條(NURBS)的線面求交和基于NURBS的面面求交2種方法，獲得復雜自由曲面的×點云；將×點云作為控制點構造NURBS曲面，然后把修剪后的NURBS曲面邊界按給定數目或給定長度劃分，連接參數域上的邊界節點后得到參數域網格，將其映射回空間曲面。對邊界處網格進行投影處理以減少曲面擬合出現的邊界褶皺及內縮問題。采用加密點陣技術減小曲面擬合的誤差。研究結果表明：與多曲面網格劃分方法相比，采用曲面擬合及映射法能夠得到線條流暢、大小基本一致的網格，具有良好的建筑美學效果。

非均勻有理B樣條(NURBS)；復雜自由曲面；曲面擬合；映射法；網格劃分

隨著計算機科學技術的進步、建筑施工工藝的發展和人們建筑審美水平的提高，自由曲面結構以其優美的造型越來越多地出現在人們的視野當中。“自由曲面”指無法用單個或幾個解析函數表達的曲面，也可理解為那些明顯區別于傳統建筑造型的曲面[1]。由于解析曲面具有一定的周期性或規律性，其網格劃分比較方便。而自由曲面的不規則性使傳統的網格劃分方法難以適用于自由曲面結構。因此，如何在自由曲面上生成線條流暢、大小基本一致的網格，是空間結構領域的熱點和難題[2]。網格劃分起源于有限元領域[3]，常用的方法有Delaunay法[4]、波前法[5]、映射法[6]等。但有限元領域的網格劃分方法難以滿足建筑美學線條流暢、大小基本一致的要求。因此，近年來有研究者針對自由曲面的建筑網格劃分進行了相關研究，如：WINSLOW等[7]以桿件走向為優化變量，以結構性能為目標函數，用遺傳算法實現自由曲面的多目標優化；SU等[8]繪出自由曲面的主應力跡線，采用改進的波前法自動生成網格；潘煒等[9]按照展開前、后面積變化最小的原則展開曲面，并利用線推進法生成平面網格，最后映射回空間曲面；丁慧等[10]提取等參線并以桿件長度相等為條件分割等參線，連接等參線上的節點生成網格。復雜自由曲面由多個非均勻有理B樣條(NURBS)裁剪曲面組成，且存在內部空洞等復雜情況。針對該類自由曲面，現有的網格劃分方法是在每個裁剪曲面上分別劃分網格，然后對交界附近網格進行調整。該方法的缺點是網格劃分不易進行，交界處網格不好調整，難以達到建筑美學線條流暢的要求。本文作者提出基于NURBS的線面求交和面面求交2種方法，獲得復雜自由曲面的×點云。第1種方法是構造矩形×平面點陣，過每個點作平行于Z坐標軸的射線與NURBS曲面求交，得到×點陣；第2種方法是根據NURBS曲面的特征，構造個平面并與NURBS曲面求交，對交線均勻采樣個點，修補邊界后得到點陣。利用向心參數化方法得到點陣的和向節點矢量，構造以為控制點陣的NURBS曲面。將修剪后的NURBS曲面邊界按給定數目或給定長度劃分，連接參數域上的邊界節點后形成參數域網格，將其映射回空間曲面，對邊界處網格作投影處理，即可得到線條流暢、大小基本一致的四邊形網格。

1 曲面擬合

曲面擬合技術在逆向工程和計算機輔助設計等領域中得到了廣泛應用[11]。利用計算機視覺技術(如激光掃描)對自由曲面進行數字化，可得到大量散亂數據點，根據數據點集可得到實物的CAD模型[12]。

在建筑工程領域，逆向工程用于古建測繪和古建保護、快速建立城市模型、空間網格結構的逆向建模等方面。李娜[13]借鑒逆向工程的操作原理，利用激光三維掃描系統進行實物樣件的點云數據采集，采用蒙皮法進行曲面造型，然后進行網格劃分。該技術基于對實物進行激光掃描得到大規模散亂數據點。在復雜自由曲面網格劃分時，一般建筑師已經提供符合其設計意圖的曲面CAD模型；為了獲得線條流暢、大小基本一致的網格，本文作者提出基于NURBS的線面求交和面面求交2種方法，獲得復雜自由曲面的×點云，構造以×點云為控制點陣的NURBS曲面，為映射法劃分網格提供基礎。

圖1所示為某工程CAD模型。下面以圖1為例，介紹基于NURBS的線面求交法和基于NURBS的面面求交法。

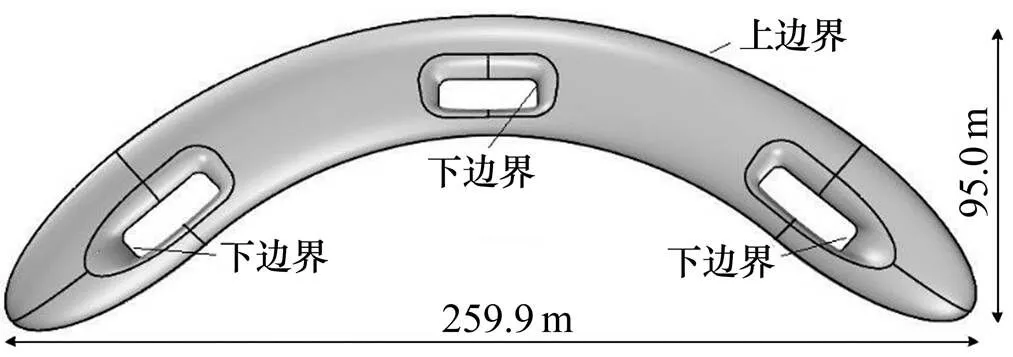
圖1 某工程CAD模型

1.1 基于NURBS的線面求交法

根據NURBS曲面的強凸包性[14]和控制點陣為矩形拓撲[12]的特點，構造1個×矩形平面點陣作射線與NURBS曲面求交，提取原曲面信息。算法流程如圖2所示。

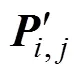
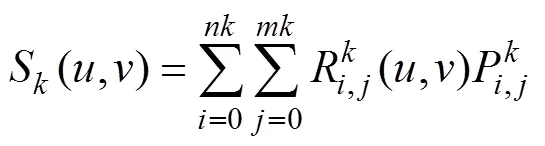
圖2 基于NURBS的線面求交法流程圖

Fig. 2 Flow chart of NURBS based ray-surface intersection method

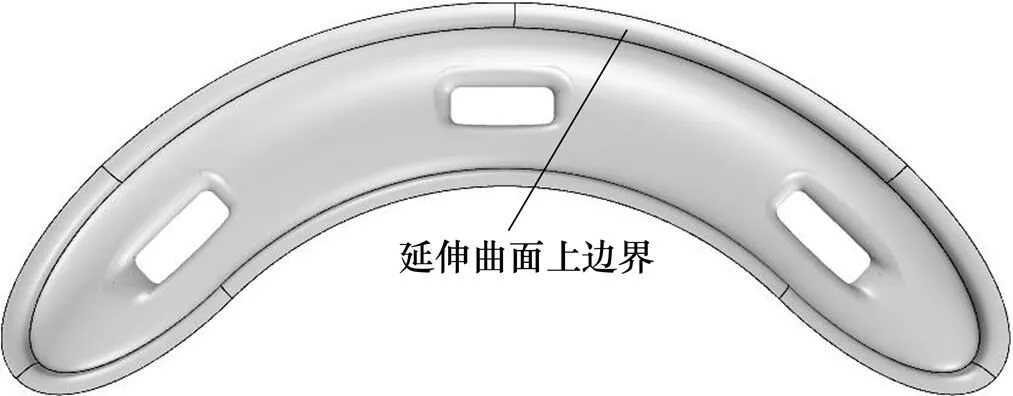
圖3 延伸曲面上邊界

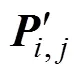
圖4 N×M矩形點陣及曲面包圍盒

NURBS曲面與射線求交是一種基礎的幾何算法，常用于雷達散射截面計算(RCS)的射線追蹤計算[15]、逆向工程中曲面的制造誤差計算[16]等方面。

首先利用Krawczyk算子判斷式(1)在某一區間是否存在解，然后對存在唯一解的區間給定1個初值，利用牛頓迭代法求解。詳細流程參見文獻[16]。

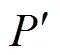
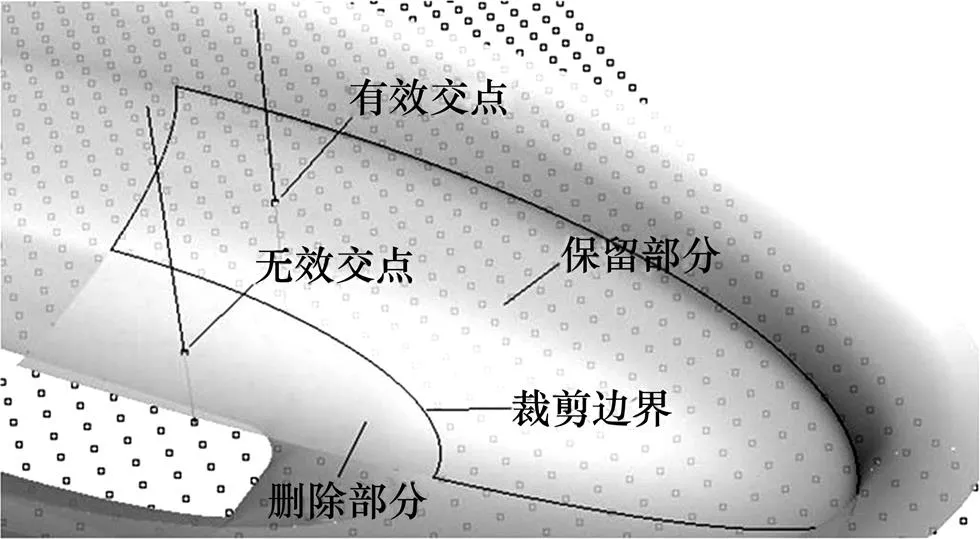
圖5 裁剪NURBS曲面的有效交點與無效交點

1.2 基于NURBS的面面求交法

前面提出一種提取原曲面信息的方法，現通過構造個平面與NURBS曲面求交提取原曲面信息。算法流程如圖6所示。

1) 補齊曲面空洞。當復雜自由曲面內部存在空洞時，為了保證平面與曲面的交線在平面上能夠擬合為一條曲線，用平面補齊空洞。補齊空洞及平面切割方式如圖7所示。

圖6 基于NURBS的面面求交法流程圖

圖7 補齊空洞及平面切割方式

2) 選擇平面切割方式。復雜自由曲面由多個NURBS裁剪曲面組成，應根據曲面各部分的走向和特征，選擇合適的切割方式，如直線式和圓弧式切割(見圖7)。原曲面由11個NURBS曲面組成(不包括補齊空洞的平面)，分為5部分切割。第1部分由平面上點1和點2及平面數1確定。首先過點1和點2作直線，然后以為正法線，等距離地作1個平面與曲面求交。第2部分由平面上點3、點4、點5及平面數2確定。首先過點4以直線為正法線作平面，然后以點4為旋轉中心，軸為旋轉軸，將平面旋轉2?1次，每次旋轉角度為∠345/(2?1)，即可得到2個平面與曲面相交。其余3個部分依此類推。

3) NURBS曲面與平面求交。用平面與CAD模型的個曲面求交，如圖8所示。平面與4個曲面相交，共有5條交線，其中與曲面2有2條交線即交線2 和4。

4) 處理同一平面上的交線(見圖8)。首先處理裁剪曲面與平面求交的情況。曲面1是裁剪曲面，其刪除部分不顯示，因此，把位于曲面1刪除部分且與平面相交的交線刪除。對曲面4進行同樣處理。平面與NURBS曲面共有5條交線，每條交線均勻采樣一定數目點，然后構造1條插值于所有采樣點的NURBS曲線。每個平面都得到1條與原曲面相交的曲線。

圖8 同一平面上交線處理

5) 擬合曲線采樣。曲面擬合中NURBS曲面的型值點或控制點必須為矩形拓撲，故得到平面和原曲面擬合后的交線后，對該交線均勻采樣個點，由此保證NURBS曲面與個平面求交后得到的點陣為矩形拓撲。

6) 補齊邊界。對于與NURBS曲面相交的第1個和最后1個平面(下面稱邊界平面)，總存在一部分曲面在邊界平面之外，其大小不能忽略。取這部分曲面的邊界線，并均勻采樣個點，可以保證完整地提取原曲面的信息。補齊邊界方式如圖9所示。

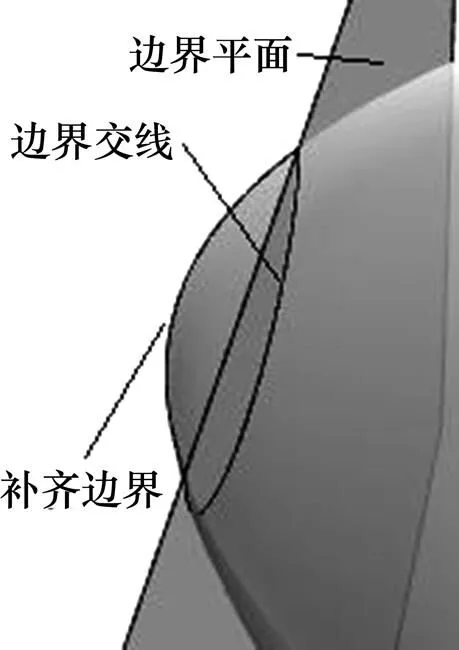
圖9 補齊邊界

經過以上步驟，可以得到矩形拓撲點陣。

1.3 擬合NURBS曲面

利用曲面擬合中常用的向心參數化[14]方法構造矩形拓撲點陣的節點矢量和。獲得點陣和節點矢量和之后，進行曲面擬合。

對于矩形拓撲點陣，傳統的曲面擬合方法是將其作為型值點陣，創建1個非有理的(，)次B樣條曲面(,)，使其插值于這些點。

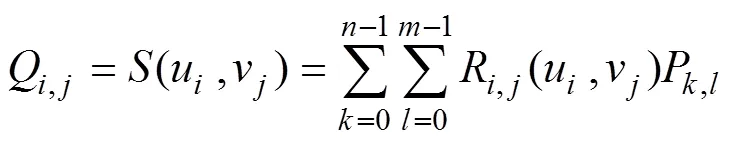
式中：Q為型值點；u和v分別為其對應的和向參數值；R(u, v)為其對應的有理基函數；P為待求的控制點。

另一種方法用1個非有理的(，)次B樣條曲面(，)逼近這些點，以控制點為優化變量，滿足如下條件：

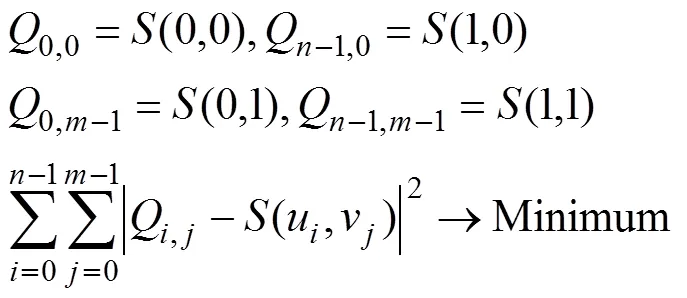
為了準確地表示復雜自由曲面，其矩形拓撲點陣的點數×不能太少。若使用插值或逼近方法，則至少需要解1個(×)×(×)的線性方程組，這將使計算時間大大增加。

針對復雜自由曲面擬合問題，采用控制點逼近方法。控制多面體是對B樣條曲面的平面片逼近，次數越低，逼近效果越好；當節點矢量無限加細時，控制多面體將收斂于曲面[17]。因此，以為控制點陣，在節點矢量和上構造非有理的雙二次B樣條曲面(,)，根據CAD模型的原有邊界情況對(,)進行裁剪。基于NURBS的線面求交法和面面求交法的擬合曲面與裁剪曲面分別如圖10和圖11所示，2種求交方法的擬合曲面雖不盡相同，但裁剪曲面都能反應復雜自由曲面的特征，可為映射法網格劃分提供基礎。

(a) 擬合曲面；(b) 裁剪曲面

(a) 擬合曲面；(b) 裁剪曲面

2 映射法劃分網格

圖12所示為映射法劃分網格示意圖。建筑師提供的CAD模型由3個曲面構成(見圖12(a))，利用基于NURBS的線面求交法，將3個NURBS裁剪曲面擬合為1個曲面(見圖12(b))，利用映射法劃分網格。

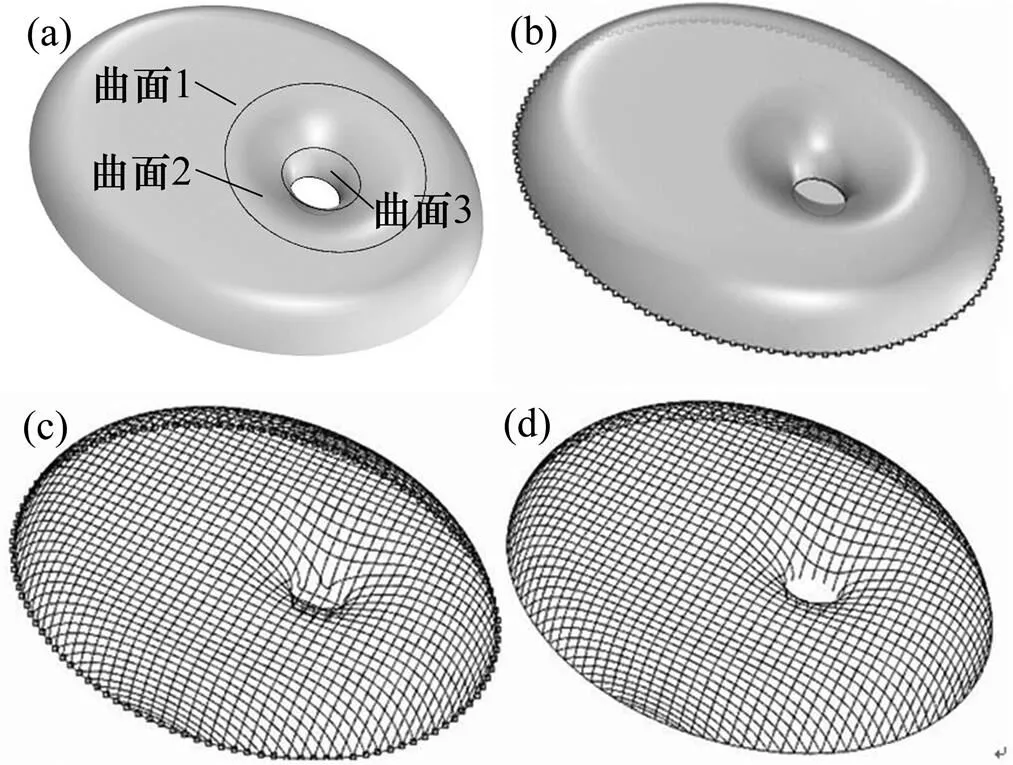
(a) 某工程CAD模型；(b) 邊界等長度分段；(c) 空間曲面上網格；(d) 處理后網格

1) 將空間曲面邊界分段。以二分法為基礎，將空間曲面的邊界按弦長分段。分段方式有給定長度、給定段數、等比例或指定長度數組等(見圖12(b))。

2) 將分段點投影回參數域，連接參數域上的分段點后形成參數域網格。分段后的邊界點反向映射回參數域中，在參數域中將邊界點按照建筑師期望的走向依次連直線。

3) 將參數域網格映射回空間曲面，得到空間網格(見圖12(c))。

4) 處理邊界處網格。由圖12(c)可知：用映射法在擬合曲面上畫出的網格在原有曲面交界處線條流暢，但在擬合曲面的邊界處質量不佳，為此需處理邊界處網格。下面介紹該具體方法。

3 算例與比較

3.1 2種求交方法的比較

前面以圖1為例詳細介紹了基于NURBS的線面求交法(以下簡稱方法一)及基于NURBS的面面求交法(以下簡稱方法二)的算法流程。表1所示為2種方法的比較結果(其中，為將復雜自由曲面擬合為1個曲面所需的時間，U為擬合曲面上邊界最大誤差，L為擬合曲面下邊界最大誤差)。

方法一耗時最久的步驟是曲面與直線求交，需進行49萬(700×700)次求交運算；方法二耗時最久的步驟是曲面與平面求交，只需進行900次求交運算。故方法二的速度遠快于方法一的速度。

表1 2種方法的比較

圖13所示為方法一邊界處褶皺。方法一中，當曲面邊界走向不嚴格為平面點陣走向時，邊界附近的控制點不能很好地還原曲面的邊界信息，出現“褶皺”問題，導致上、下邊界最大誤差較大。此時，可以通過加密平面點陣的方法來減小褶皺，但會使時間大大 增加。

圖14所示為方法二下邊界誤差。原曲面下邊界出現直角轉折，在下邊界附近的3個采樣點由此也產生較大轉折(見方法二步驟5))。因為NURBS曲面的強凸包性，擬合曲面在此處出現最大誤差為250.5 mm，可以通過加密采樣點的方法減小誤差。而上邊界處轉折較小，最大誤差僅為2.1 mm。

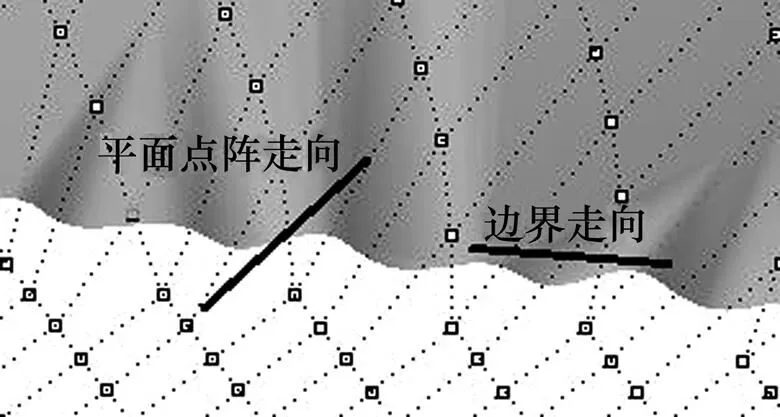
圖13 方法一邊界處褶皺

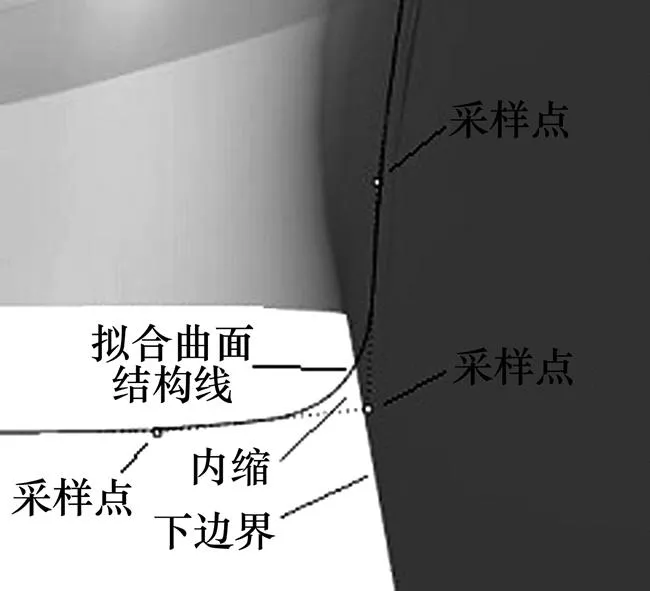
圖14 方法二下邊界誤差

2種方法除邊界處出現誤差外，其余部分誤差均小于5 mm。用映射法網格劃分時需將邊界處網格投影至原曲面以消除誤差，方法一還需手動處理因“褶皺”而畸形的網格。

通過2種方法的比較可以得出以下結論：1) 方法二比方法一復雜；2) 方法二的速度遠快于方法一的速度，最大誤差也比方法一的小；3) 利用映射法劃分網格時，2種方法均需將邊界處網格投影回原曲面，方法一還需手動處理因“褶皺”而畸形的網格。

3.2 分曲面劃分網格與曲面擬合劃分網格比較

以某工程CAD模型(見圖12(a))為例，用分曲面的方法劃分網格，如圖15所示。首先將曲面1的邊界1等長度分段，根據欲劃分的網格形式確定邊界2的分段點，最后連接邊界1分段點或同時連接邊界1、邊界2分段點(見圖15(a))。劃分好曲面1的網格后，憑經驗確定曲面2上邊界3的分段點，連接邊界2分段點或邊界2、邊界3分段點(見圖15(b))。同理畫出曲面3的網格(見圖15(c))。但上述過程依賴于工程師的經驗，且網格劃分容易失敗。

在邊界2附近，曲線1為邊界1分段點相連所得曲線，曲線2為邊界1和2分段點相連所得曲線，因此，導致網格大小不均勻(見圖15(a))。由于分別在3個曲面上劃分網格，導致邊界處網格不均勻，線條不流暢(見圖15(c))。對邊界處質量不佳的曲線進行一定調整，調整后網格均勻性有一定提高，但交界處曲線流暢性仍然不佳(見圖15(d))。

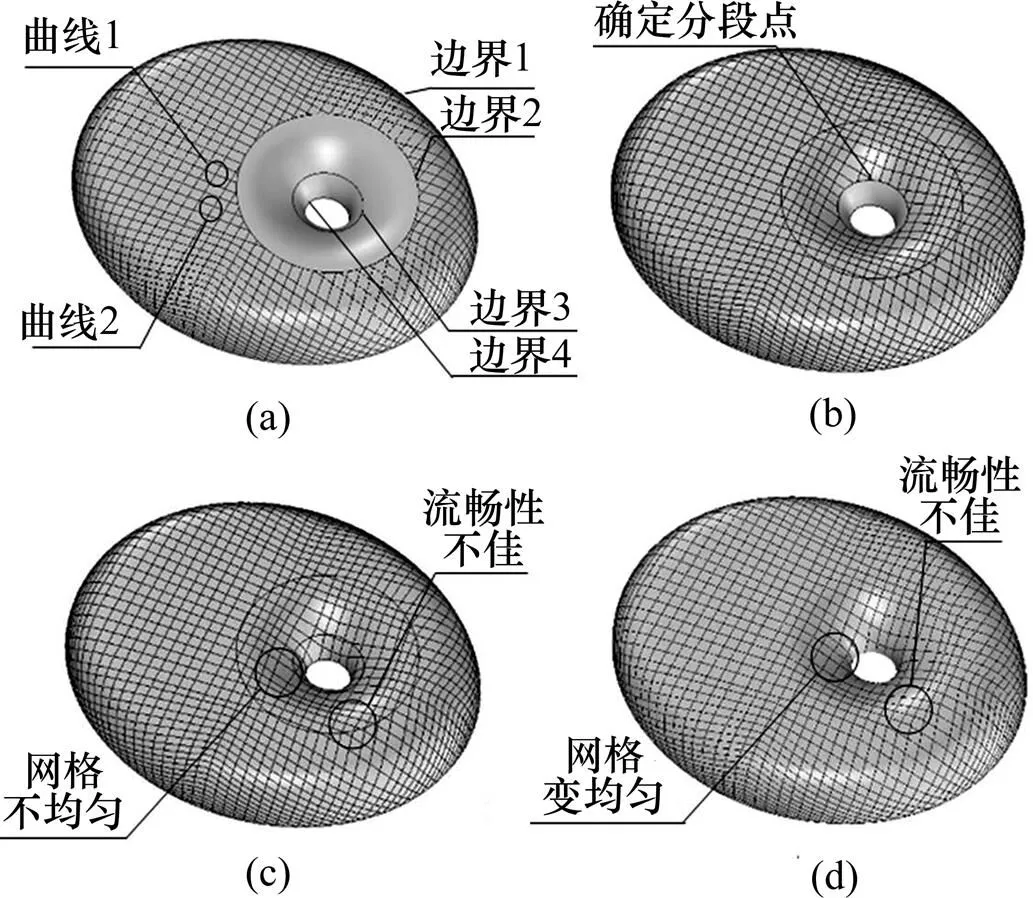
(a) 曲面1；(b) 曲面1和2；(c) 曲面1，2和3；(d) 調整后網格劃分

現用曲面擬合的方法對圖12(a)進行網格劃分。該工程平面投影為橢圓形，平面面積為146.0 m× 116.0 m。用方法一獲得600×600點陣，擬合為1個曲面，等分外邊界，在參數域上將外邊界分段點依次連為直線后將參數域網格映射回空間曲面(見圖12(c))。將邊界處網格投影回原曲面，并處理極少數因“褶皺”而畸形的網格，得到最終的網格劃分(見圖12(d))。

圖15中在原有的3個曲面上分別劃分網格，因此，在交界附近網格不均勻，線條過渡不流暢，且難以調整，網格劃分過程依賴工程師個人經驗，且容易失敗；圖12(d)中線條流暢，網格大小基本一致，且過渡均勻。雖然在邊界處出現一定誤差，但可以通過加密點陣減小誤差，或將邊界處網格投影回原曲面，以消除邊界處誤差。

4 結語

1) 提出2種點云生成方法：方法1中構造1個×矩形平面點陣并作射線與復雜自由曲面求交，從而獲得矩形拓撲點陣；方法2需合理選擇平面切割方式，將復雜自由曲面分為幾個部分，構造個平面與復雜自由曲面求交，并將多條交線擬合后均勻采樣個點，修補邊界后獲得矩形拓撲點陣。

2) 將二者進行比較，令點云為控制點陣，把復雜自由曲面擬合為1個NRUBS曲面，以映射法劃分空間網格。

3) 與分曲面劃分方法相比，曲面擬合和映射法能夠得到線條流暢、大小基本一致的四邊形網格。

[1] 沈世釗, 武岳. 結構形態學與現代空間結構[J]. 建筑結構學報, 2014, 35(4): 1?10. SHEN Shizhao, WU Yue. Structural morphology and modern space structures [J]. Journal of Building Structures, 2014, 35(4): 1?10.

[2] 李承銘, 盧旦. 自由曲面單層網格的智能布局設計研究[J]. 土木工程學報, 2011, 44(3): 1?7. LI Chengming, LU Dan. Study of intelligent layout design of single-layer lattice shell of free form surface[J]. China Civil Engineering Journal, 2011, 44(3): 1?7.

[3] LO S H. Finite element mesh generation and adaptive meshing[J]. Progress in Structural Engineering & Materials, 2002, 4(4): 381?399.

[4] SI Hang. TetGen, a delaunay-based quality tetrahedral mesh generator[J]. ACM Transactions on Mathematical Software, 2015, 41(2): 11.

[5] PIRZADEH S. Structured background grids for generation of unstructured grids by advancing-front method[J]. AIAA Journal, 2012, 31(2): 285?289.

[6] LISEIKIN V. Grid generation methods[M]. Amsterdam, Netherlands: Springer, 2010: 10?14.

[7] WINSLOW P, PELLEGRINO S, SHARMA S B. Multi-objective optimization of free-form grid structures[J]. Structural & Multidisciplinary Optimization, 2010, 40(1/2/3/4/5/6): 257?269.

[8] SU Liang, ZHU Shunlai, XIAO Nan, et al. An automatic grid generation approach over free-form surface for architectural design [J]. Journal of Central South University, 2014, 21(6): 2444?2453.

[9] 潘煒, 吳慧, 李鐵瑞, 等. 基于曲面展開的自由曲面網格劃分[J]. 浙江大學學報(工學版), 2016, 50(10): 1973?1979. PAN Wei, WU Hui, LI Tierui, et al. Grid generation on free-form surface based on surface flattening[J]. Journal of Zhejiang University: Engineering Science, 2016, 50(10): 1973?1979.

[10] 丁慧, 羅堯治. 自由形態網殼結構網格生成的等參線分割法[J]. 浙江大學學報(工學版), 2014, 48(10): 1795?1801. DING Hui, LUO Yaozhi. Isoparametric line dividing grid generation method for free-form lattice shells[J]. Journal of Zhejiang University: Engineering Science, 2014, 48(10): 1795?1801.

[11] BRUJIC D, AINSWORTH I. Fast and accurate NURBS fitting for reverse engineering[J]. The International Journal of Advanced Manufacturing Technology, 2011, 54(5): 691?700.

[12] 來新民, 黃田. 基于NURBS的散亂數據點自由曲面重構[J]. 計算機輔助設計與圖形學學報, 1999, 11(5): 433?436. LAI Xinmin, HUANG Tian. NURBS based approach of surface reconstruction from scattered data[J]. Journal of Computer Aided Design and Computer Graphics, 1999, 11(5): 433?436.

[13] 李娜. 空間網格結構幾何形態研究與實現[D]. 浙江大學建筑工程學院, 2009: 77?92. LI Na. Research and implementation of geometric configuration of space grid structures[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2009: 77?92.

[14] PIEGL L, TILLER W. The NURBS book[M]. New York, USA: Springer, 1995: 94?95.

[15] 官火梁, 吳強, 席平. RCS計算中NURBS曲面和射線求交的快速計算[J]. 圖學學報, 2006, 27(1): 87?91. GUAN Huoliang, WU Qiang, XI Ping. A fast algorithm for intersection calculation of ray and NURBS surface in predicting radar cross section calculation[J]. Journal of Engineering Graphics, 2006, 27(1): 87?91.

[16] 王保慶, 張俐, 李東升. 逆向工程中NURBS曲面與直線交點快速計算[J]. 圖學學報, 2010, 31(2): 155?158. WANG Baoqing, ZHANG Li, LI Dongsheng. Rapid calculation of intersection points between NURBS surface and line in Reverse Engineering[J]. Journal of Engineering Graphics, 2010, 31(2): 155?158.

[17] BOOR C D. Cutting corners always works[J]. Computer Aided Geometric Design, 1987, 4(S1/2): 125?131.

Grid generation on complex free-form surface based on surface fitting

CHEN Lijie1, WU Hui2, LI Tierui1, GAO Boqing1

(1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China;2.Public Administration College, Zhejiang University of Finance & Economics, Hangzhou 310018, China)

In order to obtain architectural mesh of complex free-form surface, the complex free-form surface was fitted into one surface and then grids were generated using mapping method. First, two methods called NURBS based on ray-surface intersection and NURBS based on plane-surface intersection were proposed to obtain the×point cloud of complex free-form surface. Secondly, a NURBS surface was constructed using the×point cloud as control points, then the boundaries of trimmed NURBS surface were divided by a given number or a given length, and the boundary nodes of the parametric domain were connected to get parametric domain grids. After that, the grids were mapped onto the free-form surface. Lastly, the grids near the boundaries were projected onto original surfaces to reduce boundary fold and shrinkage caused by surface fitting. To reduce the error of surface fitting, the number of point cloud was increased. The results show that compared with the method which respectively generates grids on multiple trimmed surfaces, the proposed methods produce fluent and uniform grids, with good architectural aesthetics.

non-uniform rational B-splines (NURBS); complex free-form surface; surface fitting; mapping method; grid generation

10.11817/j.issn.1672-7207.2018.07.019

TU393.3

A

1672?7207(2018)07?1718?08

2017?07?02；

2017?08?20

國家自然科學基金資助項目(51378457，51678521)；浙江省自然科學基金資助項目(LY15E080017) (Projects(51378457, 51678521) supported by the National Natural Science Foundation of China; Project(LY15E080017) supported by the Natural Science Foundation of Zhejiang Province)

高博青，博士，教授，從事空間結構研究；E-mail: bqgao@zju.edu.cn

(編輯 伍錦花)