圍巖變形準則下考慮目標失穩概率的巖石隧道可靠度逆向計算

李翔，李夕兵，周子龍

?

圍巖變形準則下考慮目標失穩概率的巖石隧道可靠度逆向計算

李翔，李夕兵，周子龍

(中南大學 資源與安全工程學院，湖南 長沙，410083)

針對軟弱質巖石環境下的隧道圍巖變形機制，建立基于圍巖變形失穩控制的極限狀態方程。為了研究其相應的可靠度逆向問題即在已知目標失穩概率條件下，反求工程參數以確保滿足預先規定的可靠度水平，引入逆向可靠度方法并歸納其具體的計算實施流程。采用該方法驗證其在巖石隧道可靠度逆向分析過程中待求工程參數的計算精度和效率，分析待求工程參數在不同初值條件下對計算結果的影響。在此基礎上，考慮不同水平的目標失穩概率，通過該方法開展基于圍巖變形準則的巖石隧道穩定性設計。研究結果表明：逆向可靠度方法對于待求工程參數能以較高效率獲得滿意的計算結果，且其初值選取不會影響該方法求解的準確性，僅對其收斂速度有一定影響；利用逆向可靠度方法可方便調控待求工程參數值，為巖石隧道工程設計提供參考依據。

巖石隧道；圍巖變形；目標失穩概率；逆向可靠度；穩定性設計

眾所周知，現代巖石隧道支護的核心觀點之一是將圍巖自身視為支護結構的重要組成部分，強調最大限度地發揮圍巖自承作用，通過現場監控量測，適時設置支護。這一動態設計思想(即信息化設計)的實施過程主要取決于有無圍巖變形(如洞周收斂、拱頂下沉等)的量測[1]。圍巖變形是隧道力學行為最明顯最集中的反映，掌握了圍巖變形過程也就把握了隧道穩定狀 態[2]。采用圍巖變形來判別隧道穩定性，較易借助工程類比總結經驗，針對允許變形值建立相關判別準則，進而對這種宏觀量測信息反映的隧道穩定狀態及時作出判別和反饋[3?4]，其相關應用已納入公路[5]、鐵路[6]等巖石隧道工程規范。鑒于決定上述巖石隧道穩定性的巖質材料及賦存條件等眾多因素存在無法忽視的不確定性，與傳統的定值(或確定性)方法相比，可靠度方法通過求解失穩概率等表征指標，更明確地考慮這些不確定性對其穩定狀態的影響[7?12]。這些研究關注的重點旨在探討失穩概率(或可靠度指標)計算方法及評判其失穩概率，從分析過程上看，它們均是在已知工程設計參數(如錨噴支護體系中的錨桿支護阻力等)情形下求解失穩概率，以該概率表征指標值體現圍巖失穩風險。這一過程通常視為可靠度的正向分析過程，相應的方法稱為正向可靠度方法(forward reliability method)[13?14]。在實際工程應用中，一般需根據巖石隧道的工程重要性、破壞性質以及失穩后果等因素選定用于其穩定可靠度分析的目標失穩概率(即可接受的失穩概率值或可靠度指標，反映設計允許的風險水平)[15?16]。這要求在此過程中解決1個關鍵問題，即當預先已知目標失穩概率時，如何調控與圍巖加固處治措施有關的上述工程設計參數，以便直觀地為其穩定可靠度分析提供指導依據，進而通過控制圍巖變形達到降低失穩風險水平的設計目標。顯然，與前述可靠度的正向分析過程相比，這一過程可視為可靠度的逆向分析過程。事實上，當前有關工程結構的設計規范已逐步發展為通過預先定義目標可靠度水平(對應目標失穩概率或目標可靠度指標)來確保結構安全，即結構允許的風險水平在設計前已根據其破壞類型及安全等級預先給予規定，如國內的GB/T 50283—1999“公路工程結構可靠度設計統一標準”[17]、GB 50153—2008“工程結構可靠性設計統一標準”[18]、GB 50199—2013“水利水電工程結構可靠性設計統一標準”[19]以及ISO2394—2015[20]等。相應地，在此工程背景下，為滿足依據目標失穩概率開展穩定可靠度分析的發展趨勢，需通過反求有關工程設計參數來確保滿足預先規定的可靠度水平。由此可知，這必然涉及可靠度的逆向分析問題。需指出的是：對于此類問題的解決，從理論上講，仍可沿襲傳統意義上的可靠度分析方法，即在可靠度正向求解框架內，通過試算糾錯(trial and error)方式[8, 21]求得滿足目標失穩概率的工程設計參數。但是，這種方式需人為針對設計參數值進行不斷修改、反復調試直至失穩概率計算值達到目標值水 平[22?23]，由此造成分析流程繁瑣、求解效率低，工程實際應用顯然極為不便[13?14]；此外，上述不斷修改、反復調整的過程往往帶有很大主觀隨意性或盲目性，可能導致后續可靠度計算出現較大困難，甚至難以實現[14]。這些局限性使得傳統意義上的可靠度分析方法應用于逆向分析問題時，不具備工程普遍適用性而難以推廣，實際應用受到很大限制，因此，有必要針對該問題尋求合理有效的解決途徑。為此，本文引入旨在專門解決上述問題的逆向可靠度方法(inverse reliability method)[13?14, 24]，圍繞其在巖石隧道穩定可靠度逆向問題分析領域的初步應用進行研究。首先，以軟弱質巖石環境下的圍巖變形機制為例，導出其在圍巖變形失穩控制下的極限狀態方程；然后，基于此極限狀態方程，探討逆向可靠度方法解決巖石隧道可靠度逆向分析問題時的適用性；最后，考慮到不同的目標失穩概率，利用逆向可靠度方法，開展基于圍巖變形準則的巖石隧道穩定性設計，以期為確定控制圍巖變形失穩需進一步采取的工程處治措施提供相關依據。

1 基于圍巖變形控制的極限狀態方程

1.1 圍巖變形的基本力學分析模型

HOEK[25?26]針對軟弱質巖石(weak rock)隧道施工開挖時圍巖與支護間相互作用關系進行分析，其中，為便于理解并清晰闡述圍巖如何變形、支護系統如何控制這些變形等有關問題，依據DUNCAN FAMA[27]開展的彈塑性力學分析工作建立了圍巖與支護間相互作用的基本模型，見圖1。在該經典模型中，圍巖視為靜水應力場中均質、各向同性連續介質，并設該巖石隧道開挖半徑為0，受到的水平與豎向地應力均為0，洞室周邊施加均勻的支護應力為s，圍巖彈性模量、泊松比、內摩擦角和黏聚力分別為，，和。

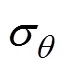
且彈性區內應力需滿足平衡方程：

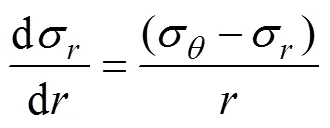
若將p(對應洞室周邊塑性區)和cr(為洞室周邊圍巖剛開始破壞時的最小支護阻力，又稱臨界應力)分別視為彈塑性邊界處的半徑和正應力，彈性區(＞p)應力則可表示為

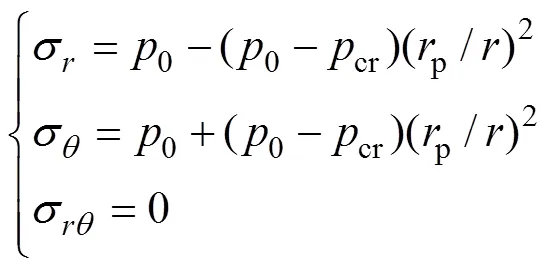
相應地，塑性區(＜p)應力表達形式為

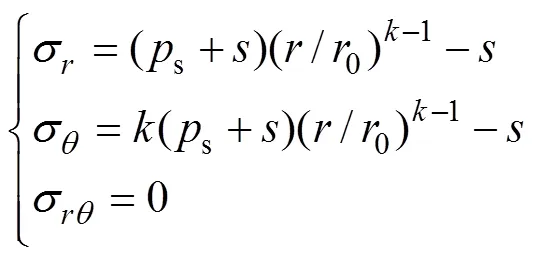
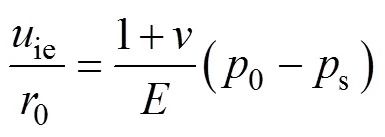
當支護阻力s小于臨界應力cr時，圍巖將出現破壞，洞室周邊塑性區半徑p可表示為

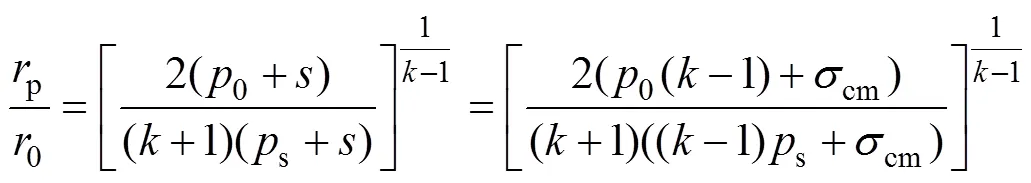
在此基礎上，為求解得到圍巖徑向塑性位移，在其塑性變形破壞過程中出現沿相互交切的結構面滑動時，假定塑性體積變化為0。對于圍巖線彈性環(r≤≤r+1)[27]，設相應的彈性模量和泊松比分別為E和，則圍巖在處對應的徑向位移表示為

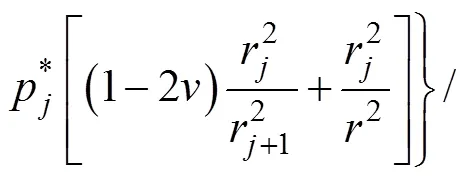
式中：p*=p–λ0；p為=r時的徑向應力。λ由下式獲得：

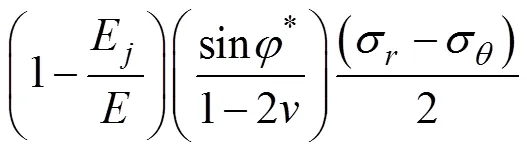
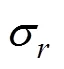
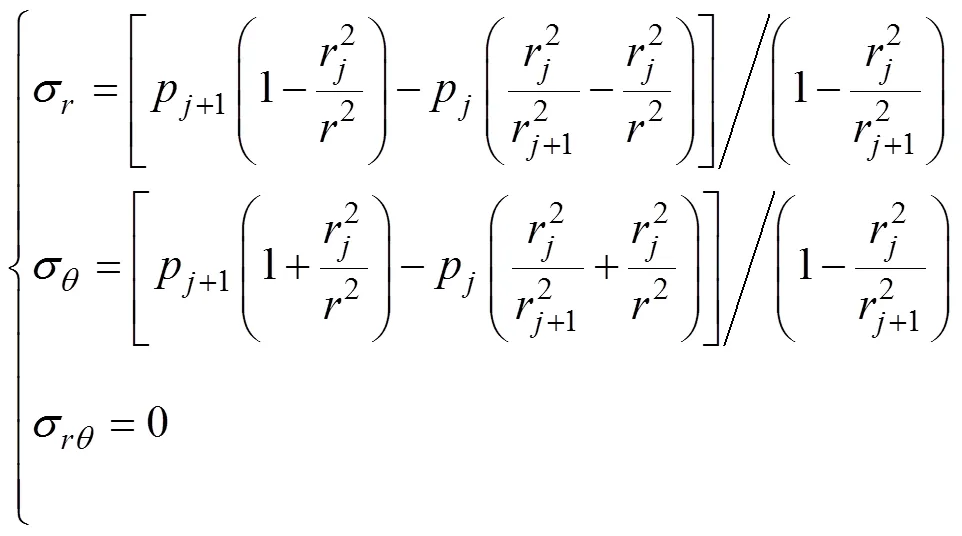
在式(8)和式(9)中，若取= 2，3→∞，則有3=0；若取=1，可得1=0，1=s，2=p，2=cr，則式(8)可轉化為

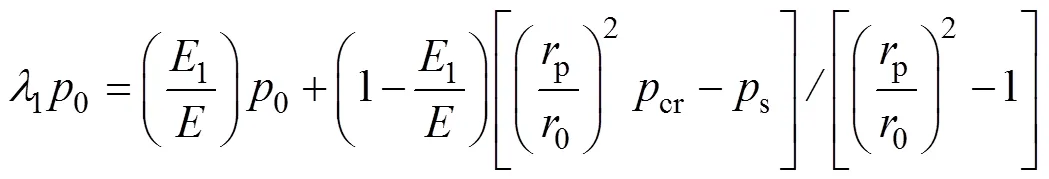
再結合式(7)和式(10)，經整理后可得圍巖徑向塑性位移ip的表達式：

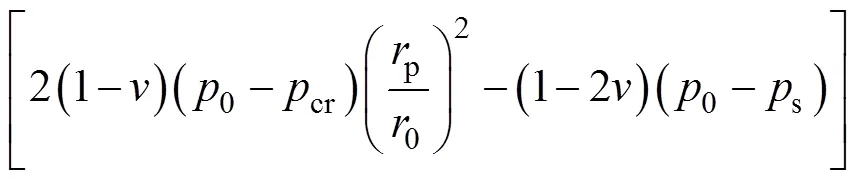
1.2 圍巖變形的極限狀態方程

極限狀態方程的建立是開展可靠度分析的基本前提。根據以上巖石隧道對應的基本力學分析模型，基于式(6)和式(11)可分別構建如下形式的極限狀態方程1()和2()：

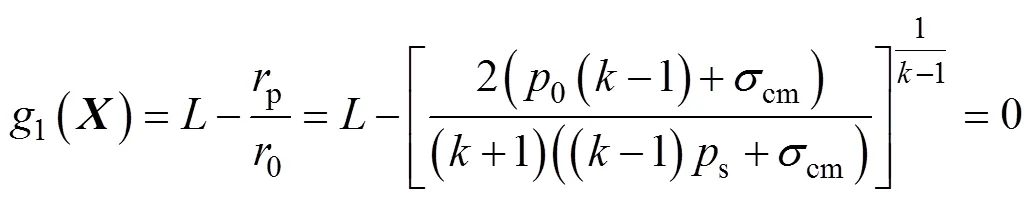
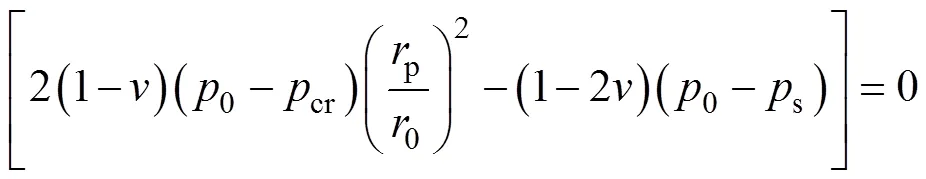
式中：為由與巖石隧道有關的基本變量組成的隨機向量；為與(p/0)有關的限值比(limiting ratio)或容許閾值比(permissible threshold ratio)[8, 10, 16, 21]；max為洞室周邊圍巖變形對應的最大允許位移，其值一般依據工程規范或經驗總結選取[7, 16]。1()表明對于圍巖塑性區的發展，當塑性區半徑p與開挖半徑0之比(p/0)不超過時，可認為圍巖是穩定的；2()表明若圍巖塑性位移(或預計最終位移)ip不超過位移限值max，則意味著圍巖是穩定的。

2 逆向可靠度方法

逆向可靠度方法的突出特點是當預先規定目標失穩概率后，獲得的工程設計待求參數既考慮了不確定性因素影響，又滿足了給定的可靠度水平。該方法符合當前國內外工程規范發展趨勢中依照目標可靠度水平進行設計的理念，其已成為處理工程結構可靠度問題的重要組成部分[16]。逆向可靠度方法最早可追溯至20世紀70年代關于如何處理工程結構隨機變量累計分布函數的逆向估測(inverse measure)問題[28]。從20世紀90年代起，有關可靠度逆向分析問題的研究才真正意義上開展起來，進而形成了基本的理論框 架[13?14]，并在此基礎上提出一系列改進措施[29?30]。對于逆向可靠度的定義，通常可表述為：在預先給定目標失穩概率(f)Target或目標可靠度指標Target的情形下，對于表達式

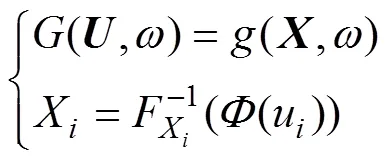
期望得到待求參數，使其獲得的可靠度水平等于目標失穩概率(f)Target。其中，隨機向量= (1,2, …,X)，表示原始空間對應的個基本變量X(= 1, 2, …,)；()和()分別為原始空間和標準正態空間中的極限狀態方程，通過對的標準正態化轉換可得到標準正態空間中隨機向量；F為X的累積分布函數；(·)為標準正態的累積分布函數。

按照對目標可靠度指標Target幾何意義的描述，它表示標準正態空間坐標原點至極限狀態曲面的最短距離，即對應以下最優化問題：

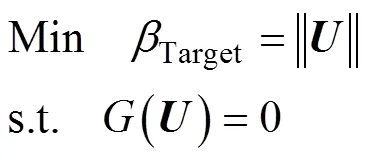
式中：= (1,2, …, u, …, u)，表示標準正態空間中隨機向量包含個基本變量u。

結合式(14)和式(15)，在驗算點處標準正態隨機向量和目標可靠度指標Target分別滿足：

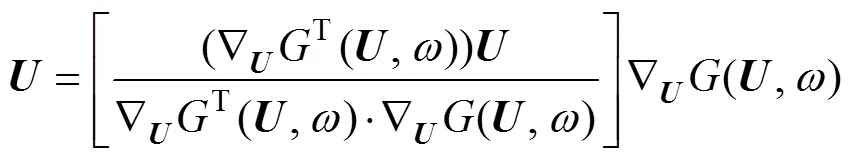
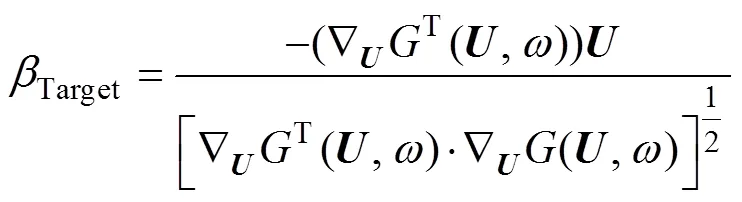
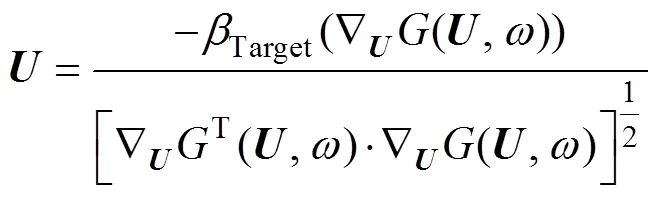
注意到標準正態隨機向量位于極限狀態曲面上，故式(14)中(,) =(,) = 0。若設待求參數的初始值為0，利用Taylor級數將標準正態空間中的功能函數()在0處展開，截取其前2項后可得

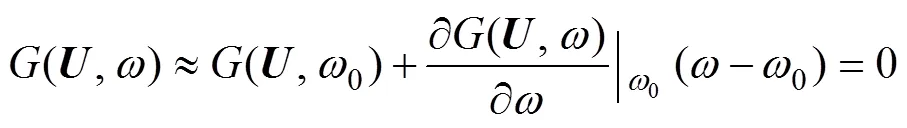
根據式(19)可進一步求得待求參數：

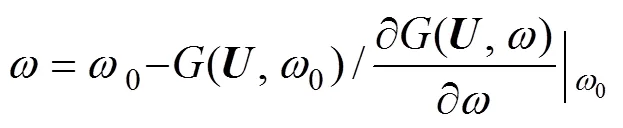
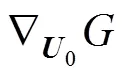
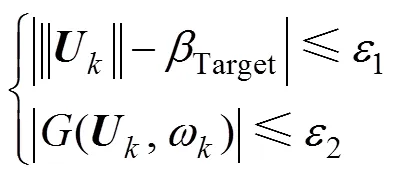
再由f=(–)計算得到目標失穩概率(f)Target。

以上給出了逆向可靠度方法基本的計算實施 流程。

3 工程算例分析

3.1 可靠度逆向問題的待求設計參數計算

以式(12)所示極限狀態方程1()為例。該極限狀態方程被廣泛應用于正向可靠度范疇內各種不同計算方法的對比分析[8, 10, 16, 21]，其中涉及的隨機變量為：巖石內摩擦角和黏聚力，它們均服從正態分布(的均值為22.85°，標準差為1.31°；的均值為0.23 MPa，標準差為0.068 MPa)；開挖半徑0、初始地應力0以及支護阻力s視為確定性參數，且0= 2.5 m(對應= 3.0)，0= 2.5 MPa。s則根據計算需要可分別選取一系列確定值。

可靠度逆向分析問題可描述為：當預先規定目標失穩概率(f)Target(或目標可靠度指標Target)時，如何由式(12)反求維持圍巖穩定所需的支護阻力s，即待求工程設計參數(設為d)。為便于說明在解決該可靠度逆向問題時采用本文方法的可行性和準確性，首先考慮在可靠度正向分析范疇內，支護阻力s作為已知工程參數，可分別取0，0.05，0.10，0.15，0.20，0.25，0.30，0.35，0.40和0.45 MPa，進而通過式(12)求得10個相應的可靠度指標Foraward和驗算點；然后，將以上由可靠度正向計算獲得的這10個可靠度指標Foraward視為可靠度逆向分析中的目標可靠度指標Target，即Target=Forward；同時，將支護阻力s視為工程設計未知的待求參數d。根據這些給定的目標可靠度指標，采用本文逆向可靠度方法反求每個目標可靠度指標Target對應的d，計算結果見表1。

從表1可見：在計算精度上，對于每個給定的目標可靠度指標Target，通過本文逆向可靠度方法計算得到的待求設計參數d(支護阻力)與可靠度正向分析中支護阻力s作為已知工程參數時的值一致，且求得的驗算點值與通過可靠度正向分析獲得的驗算點值也非常接近；在計算效率上，可靠度逆向分析過程計算工作量較少，只需5~9次迭代就可得到相應結果。

需指出的是：對于以上逆向可靠度方法的實施過程，待求設計參數計算需預設其初始值(見式(19)和式(20))。因此，為進一步探究其初始值選取對可靠度逆向計算結果的影響，以表1中可靠度正向分析涉及的支護阻力s=0.3 MPa，對應可靠度指標Forward=2.580 9為例，當采用本文逆向可靠度方法時，設目標可靠度指標Target=Forward=2.580 9，并試取待求設計參數d的初始值分別為0.001，0.005，0.010，0.050，0.100，0.500，1.000，1.500，2.000，2.500，3.000和3.500 MPa，進而依次求得d相應的計算結果，如表2所示。

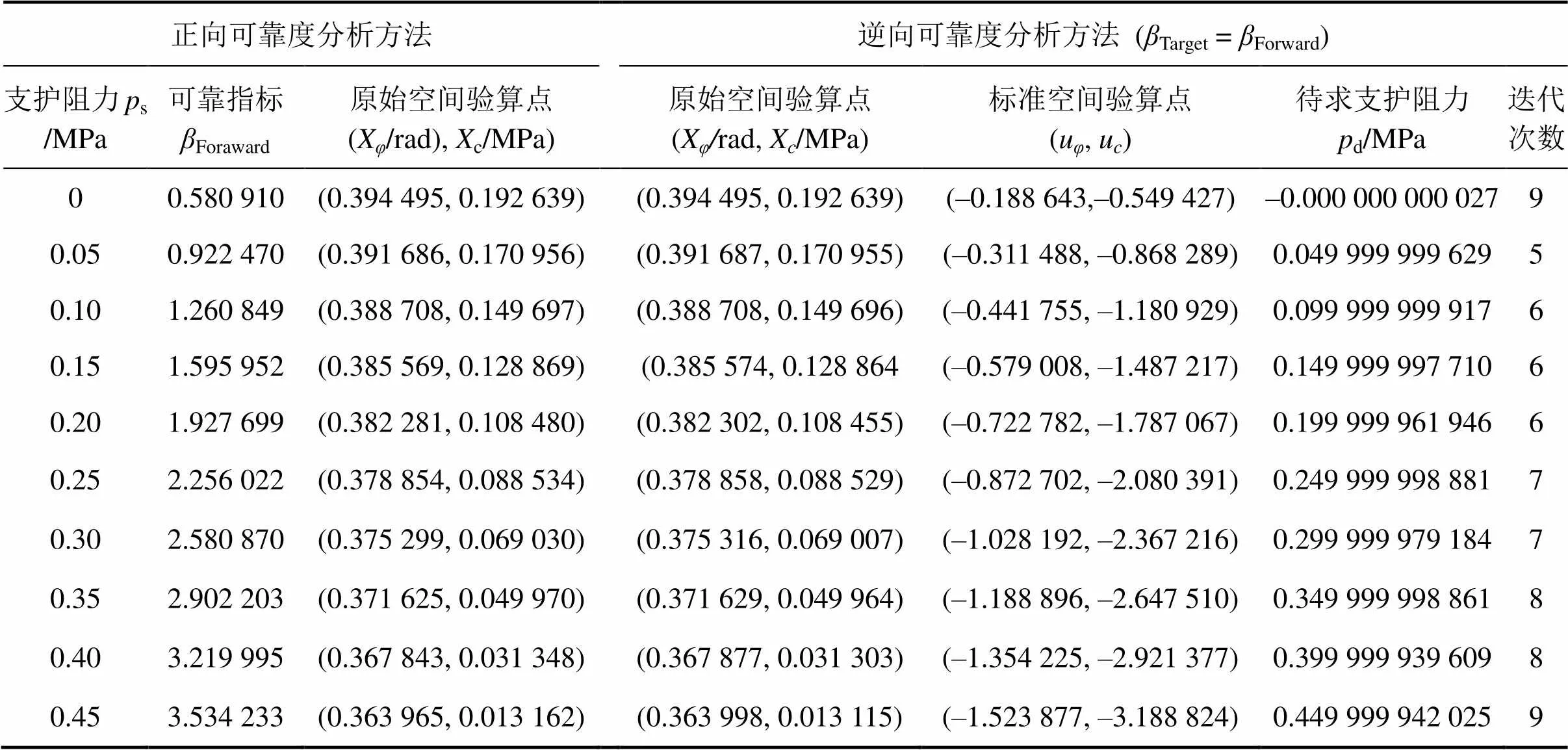
表1 可靠度逆向分析的待求參數pd(支護阻力)計算結果

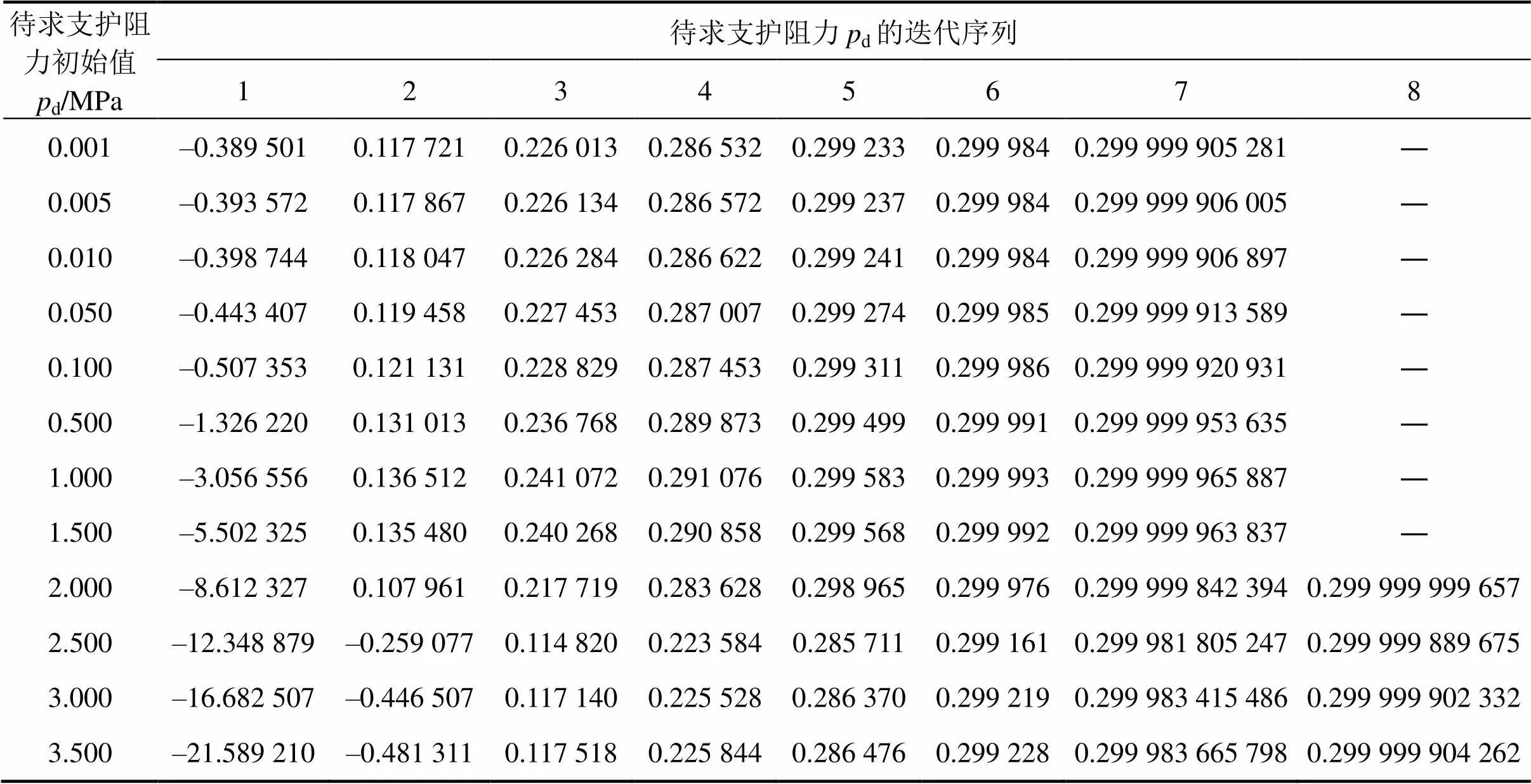
表2 待求參數pd(支護阻力)不同初始值時的計算分析過程

分析表2可知：雖然可靠度逆向計算過程中待求支護阻力d選取的初始值不同，但均可求得相應的計算結果，并收斂于d≈0.3 MPa，這與可靠度正向分析中作為已知參數的支護阻力s是一致的，表明待求參數d初始值的選取不會影響其最終計算結果；待求支護阻力d初始值僅對其迭代收斂次數產生一定影響，如當d初始值取0.001~1.500 MPa時，迭代次數為7次；當d初始值取2.000~3.500 MPa時，迭代次數為8次，但它們之間差別不大。

3.2 基于可靠度逆向分析的穩定性設計

如前所述，目前在各類巖石隧道信息化設計中，圍巖變形信息是此類隧道整體穩定性最直接、最能反映本質和總體的宏觀表現。在該過程中，通常以洞室周邊位移的變化發展來掌握巖石隧道經受各種因素作用的力學動態，進而將有關允許變形值作為圍巖穩定性設計的依據。由式(13)可見：將圍巖位移限值max視為洞室周邊的最大允許位移，當利用該位移限值進行穩定性設計時，若量測的位移未達到或不超過max(或預計最終位移將不超過這一位移限值)，則意味著圍巖是穩定的，反之則趨于不穩定，需采取加強處治措施等支護手段。

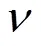
據圖2，當已知目標失穩概率(f)Target時，按照巖石隧道穩定性設計過程中針對圍巖位移限值max的要求，即可獲得對應的待求支護阻力d，以確保巖石隧道穩定可靠度滿足預先給定的可靠度水平。以圖2(a)為例，當目標失穩概率(f)Target=15.87%(對應可靠指標Target=1.0)時，若(max/0)=0.004，則穩定性設計所需d需達到1.527 4 MPa；若(max/0)=0.010，則所需d將減少至0.694 6 MPa；若(max/0)=0.03，則所需d將進一步減小至0.137 2 MPa。對于圖2中其余各分圖，可采取類似方式獲得待求支護阻力d。因此，對于預先給定的目標可靠度水平，通過圖2可方便地調控待求支護阻力，使其能直觀地為巖石隧道穩定性設計提供指導。

另外，由圖2還可看出：在一定的目標失穩概率下，隨著max/0減小，待求支護阻力d逐漸增大，曲線呈單調遞減，這表明當容許的圍巖位移限值越小，即巖石隧道穩定性要求越高時，相應的穩定性設計所需支護阻力將越大，這顯然與工程實際相符；進一步對比各分圖可知，在不同目標失穩概率下，當(max/0)取相同值時，目標失穩概率越大(或目標可靠度指標越小)，相應的待求支護阻力越小，如取(max/0)=0.004時，圖2(a)中，(f)Target=15.87%對應d=1.527 4 MPa，圖2(b)中(f)Target= 6.68%對應d=1.633 6 MPa，圖2(c)中(f)Target=2.28%對應d=1.763 3 MPa，圖2(d)中(f)Target=0.62%對應d=1.939 9 MPa；當(max/0)取其他值時，也可進行類似分析。這說明在一定圍巖位移限值條件下，隨著目標失穩概率減小即巖石隧道穩定性設計時要求的可靠度越高，則所需支護阻力越大，這顯然也與工程實際相符。

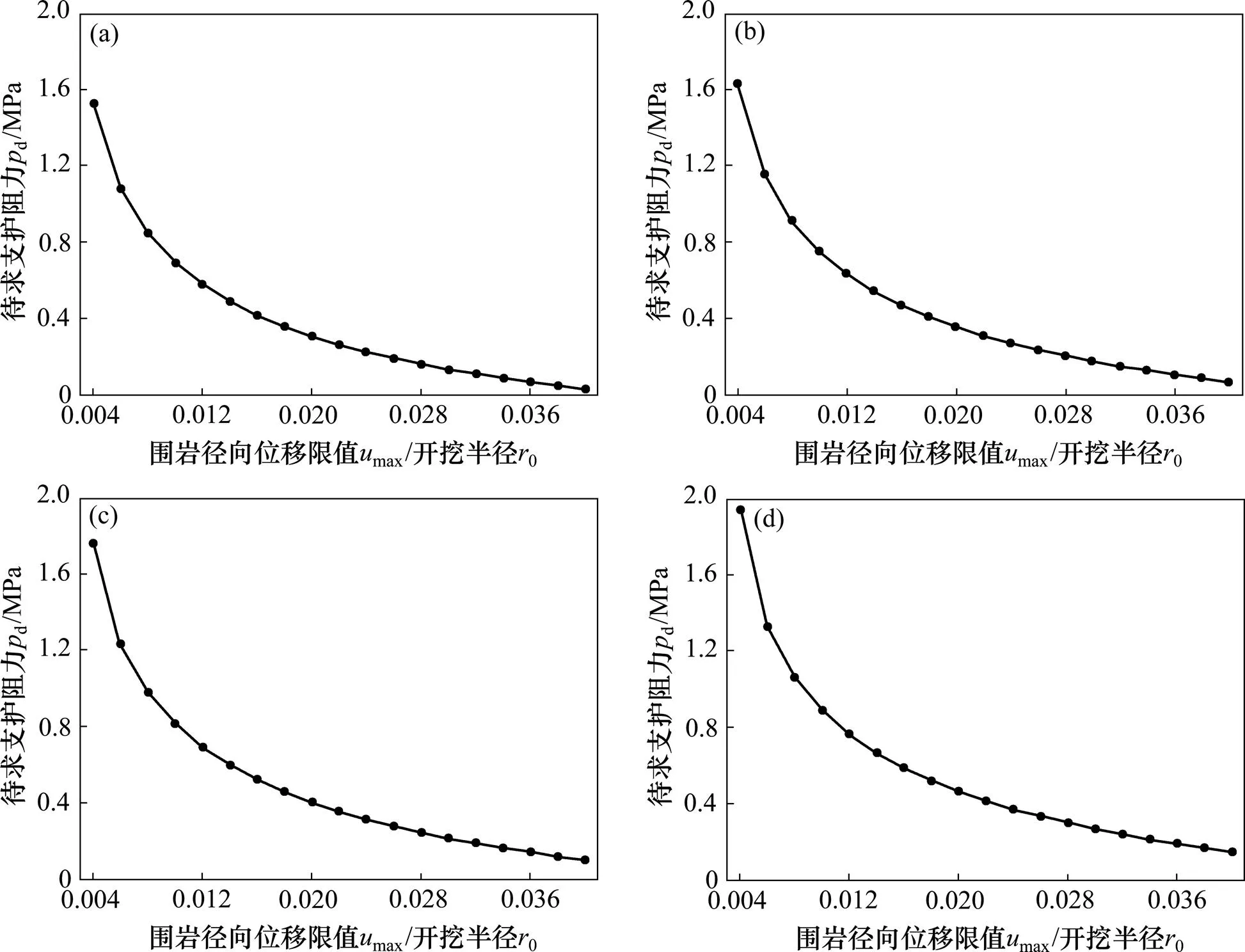
(Pf)Target：(a) 15.87%；(b) 6.68%；(c) 2.28%；(d) 0.62%

4 結論

1) 對于預先給定的目標可靠度水平，采用逆向可靠度方法計算巖石隧道工程待求參數時，能夠得到滿意的求解結果，且計算效率高，數值穩定性好。

2) 待求參數初始值的選取不會影響逆向可靠度方法的最終計算結果，不同初始值僅對其求解過程中迭代次數產生一定影響，但差別不大。

3) 通過基于可靠度逆向分析的穩定性設計，可方便地調控待求支護阻力，使其直觀地為巖石隧道工程設計提供與實際情形相符的指導依據：對于一定的目標失穩概率，容許的圍巖位移限值越小，支護阻力需求越大；對于一定的圍巖位移限值，目標失穩概率值減小，支護阻力需求越大。

[1] 李世煇. 隧道支護設計新論—典型類比分析法應用和理論[M]. 北京: 科學出版社, 1999: 1?47. LI Shihui. A new concept of tunnel support design?application and theory of precedent type analysis[M]. Beijing: Science Press, 1999: 1?47.

[2] 景詩庭, 朱永全, 宋玉香. 隧道結構可靠度[M]. 北京: 中國鐵道出版社, 2002: 83?127. JING Shiting, ZHU Yongquan, SONG Yuxiang. Reliability of tunnel structures[M]. Beijing: China Railway Publishing House, 2002: 83?127.

[3] SAKURAI S. Lessons learned from field measurements in tunneling[J]. Tunnelling and Underground Space Technology, 1997, 12(4): 453?460.

[4] 黃戡, 劉寶琛, 彭建國, 等. 基于遺傳算法和神經網絡的隧道圍巖位移智能反分析[J]. 中南大學學報(自然科學版), 2011, 42(1): 213?219.HUANG Kan, LIU Baochen, PENG Jianguo, et al. Intelligent back-analysis of tunnel surrounding rock displacement based on genetic algorithm and neural network[J]. Journal of Central South University(Science and Technology), 2011, 42(1): 213?219.

[5] JTG D70—2004, 公路隧道設計規范[S]. JTG D70—2004, Code for design of road tunnel[S].

[6] TB 10003—2016, 鐵路隧道設計規范[S]. TB 10003—2016, Code for design on tunnel of railway[S].

[7] 蘇永華, 李翔, 趙明華, 等. 考慮參數分布特征的隧道圍巖穩定失效概率計算[J]. 計算力學學報, 2010, 27(1): 120?126.SU Yonghua, LI Xiang, ZHAO Minghua, et al. Failure probability calculation for surrounding rock stability of tunnel considering random parameter distribution characteristics[J]. Chinese Journal of Computational Mechanics, 2010, 27(1): 120?126.

[8] Lü Q, CHAN C L, LOW B K. Probabilistic evaluation of ground-support interaction for deep rock excavation using artificial neural network and uniform design[J]. Tunnelling and Underground Space Technology, 2012, 32: 1?18.

[9] LANGFORD I C, DIEDERICHS M S. Reliability based approach to tunnel lining design using a modified point estimate method[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60: 263?276

[10] ZHAO H, RU Z, CHANG X, et al. Reliability analysis of tunnel using least square support vector machine[J]. Tunnelling and Underground Space Technology, 2014, 41: 14?23.

[11] LI X, LI X B. Practical probabilistic algorithm illustrated for stability of the Liziping tunnel, China: difference approximation- based SORM[C]// HUANG H W, LI J, ZHANG J, et al. Proceedings of the 6th Asian-Pacific Symposium on Structural Reliability and its Applications-ISBN: 978-7-5608-6303-0. Shanghai: Tongji University Press, 2016: 211?216.

[12] 朱喚珍, 李夕兵, 宮鳳強. 基于響應面法的三維H-B強度準則可靠度的研究[J]. 中南大學學報(自然科學版), 2017, 48(2): 491?497. ZHU Huanzhen, LI Xibing, GONG Fengqiang. Reliability analysis of 3d H-B strength criterion based on the response surface method[J]. Journal of Central South University(Science and Technology), 2017, 48(2): 491?497.

[13] DER KIUREGHIAN A, ZHANG Y, LI C C. Inverse reliability problem[J]. Journal of Engineering Mechanics, 1994, 120(5): 1154?1159.

[14] LI H, FOSCHI R O. An inverse reliability method and its application[J]. Structural Safety, 1998, 20(3): 257?270.

[15] 徐干成, 白洪才, 鄭穎人, 等. 地下工程支護結構[M]. 北京: 中國水利水電出版社, 2001: 300?303.XU Gancheng, BAI Hongcai, ZHENG Yingren, et al. Support structures of underground engineering[M]. Beijing: China Water & Power Press, 2001: 300?303.

[16] 李翔. 巖石隧道穩定可靠度正逆向計算及其基于魯棒性的主動設計方法[D]. 長沙: 中南大學資源與安全工程學院, 2016: 55?73. LI Xiang. Forward and inverse reliability calculations for rock tunnel stability and its robustness-based active design method[D]. Changsha: Central South University. School of Resources and Safety Engineering, 2016: 55?73.

[17] GB/T 50283—1999, 公路工程結構可靠度設計統一標準[S]. GB/T 50283—1999, Unified standard for reliability design of highway engineering structures[S].

[18] GB 50153—2008, 工程結構可靠性設計統一標準[S]. GB 50153—2008, Unified standard for reliability design of engineering structures[S].

[19] GB 50199—2013, 水利水電工程結構可靠性設計統一標準[S]. GB 50199—2013, Unified design standard for reliability of hydraulic engineering structures[S].

[20] ISO 2394—2015, General principles on reliability for structures[S].

[21] LI H Z, LOW B K. Reliability analysis of circular tunnel under hydrostatic stress field[J]. Computers and Geotechnics, 2010, 37(1/2): 50?58.

[22] LOW B K, EINSTEIN H H. Reliability analysis of roof wedges and rockbolt forces in tunnels[J]. Tunnelling and Underground Space Technology, 2013, 38: 1?10.

[23] LOW B K, PHOON K K. Reliability-based design and its complementary role to Eurocode 7 design approach[J]. Computers and Geotechnics, 2015, 65: 30?44.

[24] FONTAINE E, ORSERO P, LEDOUX A, et al. Reliability analysis and response based design of a moored FPSO in west Africa[J]. Structural Safety, 2013, 41(3): 82?96.

[25] HOEK E. Practical rock engineering[EB/OL]. [2007?06?08]. http: //www.rocscience.com/learning/hoeks-s-corner.

[26] HOEK E. Reliability of Hoek-Brown estimates of rock mass properties and their impact on design[J]. International Journal of Rock Mechanics and Mining Sciences, 1998, 35(1): 63?68.

[27] DUNCAN FAMA M E. Numerical modeling of yield zones in weak rock[C]//HUDSON J A. Comprehensive Rock Engineering. Oxford: Pergamon Press, 1993: 49?75.

[28] BIRGER I A. Probability of failure, safety factors and diagnostics, problems of mechanics of solid bodies[M]. Leningrad: Sudostroenve Publishers, 1970: 71?82.

[29] BALU A S, RAO B N. Inverse structural reliability analysis under mixed uncertainties using high dimensional model representation and fast Fourier transform[J]. Engineering structures, 2012, 37(4): 224?234.

[30] 錢云鵬, 涂宏茂, 劉勤, 等. 結構逆可靠度最可能失效點的改進搜索算法[J]. 工程力學, 2013, 30(1): 394?399.QIAN Yunpeng, TU Hongmao, LIU Qin, et al. Improved search algorithm for most probable point of structural inverse reliability[J]. Engineering Mechanics, 2013, 30(1): 394?399.

Inverse calculations for rock tunnel reliability considering target probability of failure based on deformation criterion of surrounding rock

LI Xiang, LI Xibing, ZHOU Zilong

(School of Resources and Safety Engineering, Central South University, Changsha 410083, China)

Based on the deformation mechanism in the environment of the weak rock surrounding the tunnel, the limit-state functions were developed based on the control of the deformation instability for the surrounding rock. In order to analyze the corresponding inverse reliability problem, i.e. back-calculate the engineering parameters to ensure the pre-defined level of reliability when the target probability of failure is known, an inverse reliability method was introduced and its calculation steps were also summarized. By using the method for the rock tunnel, the computational accuracy and efficiency were both verified in obtaining the engineering parameters during the inverse reliability analysis, and then the influence of their various initial values on the calculation results was investigated. Considering the different levels of the target probability of failure, the rock tunnel stability design was performed based on the deformation criterion of surrounding rock. The results show that the proposed inverse reliability method used to seek the engineering parameters can obtain satisfactory results in an economical way. Moreover, the choice of their initial values has no effect on the accuracy of the proposed method, and only has certain effect on the convergence rate during iteration. With the aid of the proposed method, the engineering parameters can conveniently be adjusted, thus providing guidelines for engineering design of the rock tunnel.

rock tunnel; deformation of surrounding rock; target probability of failure; inverse reliability; stability design

10.11817/j.issn.1672-7207.2018.07.021

TU457

A

1672?7207(2018)07?1734?08

2017?07?10；

2017?09?15

國家自然科學基金資助項目(41772313, 11472311)；中國博士后科學基金資助項目(2014M552159) (Projects(41772313, 11472311) supported by the National Natural Science Foundation of China; Project(2014M552159) supported by the China Postdoctoral Science Foundation)

李翔，博士(后)，講師，從事深部巖石力學與地下工程穩定可靠度及魯棒性設計研究；E-mail: xli_xiangli@csu.edu.cn; xl_xiangli@126.com

(編輯 陳燦華)