糧食儲藏溫度場數學模擬及試驗研究
徐慧星
(江西環境工程職業學院,江西 贛州 341000)
0 引言
自人類社會開始生產糧食以來,就有對谷物進行儲藏的習慣。據國家糧食局統計測算,我國糧食產后僅儲藏、運輸、加工等環節損失浪費量達350億kg以上。其中,農戶儲糧損失比例高達8%左右,每年因蟲霉鼠雀造成損失200億kg以上。由于儲存條件差、損失大,損失損耗逾75億kg。我國糧食供求緊張,近年來糧食進口量逐年增加,每年進口的谷物和大豆約500億kg,而每年又白白地損失浪費上千億斤糧食。
目前,糧倉大多采用溫度傳感器網絡,對其內部溫度場進行實時監測,大大增加了儲存費用,而且隨著年限的增加,安全隱患比較大,容易導致巨大損失。因此,根據傳熱學理論,采用有限元法對糧倉瞬時溫度場進行數學模擬分析,不僅可減少溫度傳感器網絡監測和維護費用,對防止糧食霉變、節能減排具有十分重要的現實意義。
1 傳熱學有限元方程概述
由傳熱學原理可知,在一定溫差下,物體內熱量會從高溫地向低溫地傳遞。在正常情況下,熱傳遞中,物體內溫度T和位置、時間成函數關系,即
T=T(x,y,z,t)
(1)
物體內某時刻各點溫度值組成的集合稱為溫度場。由于溫度同性的連續介質中,溫度場與邊界、初始二者條件方不具方向性,因此溫度場為標量場。
各向方程為
(2)
在指定物體溫度邊界ST上的控制方程為
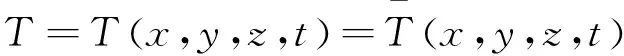
(3)
在指定物體熱流邊界Sq上的條件方程為
(4)
在指定物體對流邊界Sq上的條件方程為
(5)
初始條件為
T=f(x,y,z,t0)
(6)

(7)
取式(7)一階偏微分為0,并用矩陣表示,則有
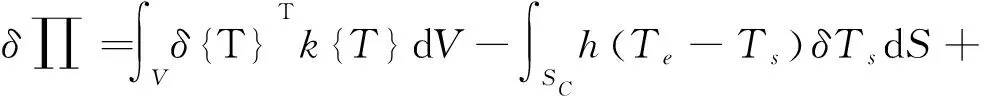
(8)
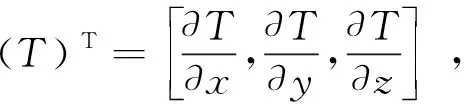
采用有限元計算方式,可以得到式(8)的溫度場有限元基本方程為
([Kk]+[Kc]){T}=
{Rb}-[C]{T}+{Rq}+[Kc]{Tc}
(9)
其中,[Kk]為物體全部熱傳導的矩陣;{T}為未知節點溫度的矩陣;[Rb]為與物體內部本身熱源等效的節點熱流矩陣;[C]為物體全部熱容矩陣;{T}為總體節點溫度的熱流矩陣;{Rq}為指定物體熱流邊界產生的等效節點熱流矩陣;[Kc]為總體對流矩陣;{Te}為指物體熱流邊界的節點環境溫度矩陣。
2 確定糧食熱物理性參數
模擬糧食儲藏倉的溫度場數值變化,首先需要了解糧食導熱系數、比熱、重力密度等熱物性參數,以上參數采用特定試驗很容易獲取。但是,由于糧食的熱物性參數變化與環境溫濕度有關,可供參考比熱參數很不容找到,且不同地方和不同時候因季節和雨水多少的變化,糧食的比熱參數更是相差甚遠。
目前,物體比熱容主要有非穩態熱流法、微量熱法、比較量熱法及混合法等測量法,結合糧食熱物性參數特性,本文采用混合法進行比熱參數的測量。混合法一般采用量熱器獲取物質比熱參數,測量過程中,只需事先在量熱器中加入些比例適合的熱水,然后加入比例適合的試樣和熱水混合,混合法所用的主要儀器是量熱器。測量時,在量熱器中預先加入一定量的熱水,再將一定溫度和質量的試樣倒入量熱器中并和熱水充分混合。混合法熱平衡方程為
C1M1ΔT1=C2M2ΔT2
(10)
其中,C1和C2分別為水和試樣的比熱容;M1和M2分別為水和試樣的質量;T1和T2分別為水和試樣的質量的溫度變化量。
根據式(8)可以得出試樣的比熱容為
(11)
由于在進行混合法熱平衡過程中會有散熱現象出現,因此需要對式(9)進行一定的改進才可以正常使用,改進主要包括兩部分內容:
1)系統散熱情況下熱容量計算方式。系統散熱對熱平衡影響較大,假設測試環境溫度不變,系統散熱量可表示為
ΔQ=CZMZKΔt
(12)
其中,△t為整個熱平衡所需要的時間(s);△Q為整個熱平衡熱量外散總和(J);K為散熱系數(K/s);CZMZ為系統熱容總和(J/K)。
量熱器熱容量需提前測定,具體辦法為:采用冷熱水混合法。加入質量、溫度為M21、T21的冷水和M22、T22的熱水,記下熱平衡所需時間Tp。假設水的比熱容為Cs,則系統散熱的熱容量可以表示為
2)比熱容計算方式。結合文章前文內容可以求出比熱容方程式為
(C0M0+C1M1)ΔT1=CMΔT2+(C0M0+C1M1)Kt3
(14)
因此,倉內糧食的比熱容可以表示為
(15)
其中,t3為加入試樣后達到熱平衡花費的時間。
3 糧倉溫度試驗測試方法
在試驗中,將溫度傳感器固定在糧倉溫度待測點位置,糧倉溫度傳感器位置圖如圖1所示。
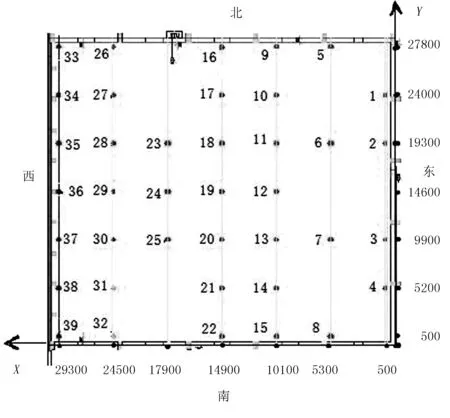
圖1 糧倉溫度傳感器位置圖Fig.1 The position diagram of granary temperature sensor
圖1中數值1~39為39個溫度測試點。試驗測試中選用某大豆種植區大豆,大豆和糧倉的熱物性參數如表1所示。為了盡量降低大豆的空氣相對濕度,減少試驗誤差,在試驗前大豆經過曬干和烘干處理,并多次進行翻動,確保整個大豆含水量和溫度一致。在大豆入倉時,保持大豆含水量和溫度的均勻一致。入倉時,水稻的平均含水量為12.5 %,溫度為28℃。
試驗開始時,開啟糧食烘干機,由烘干機風向正對面對準布置測溫點的半截面,然后倒入大豆,啟動烘干機給倉內供給熱風,測出糧倉內熱風的風速約為0.6m/s。在測試中,前12h烘干機一直工作,之后關閉烘干機,記錄整個過程中溫度傳感器網絡所測溫度值。
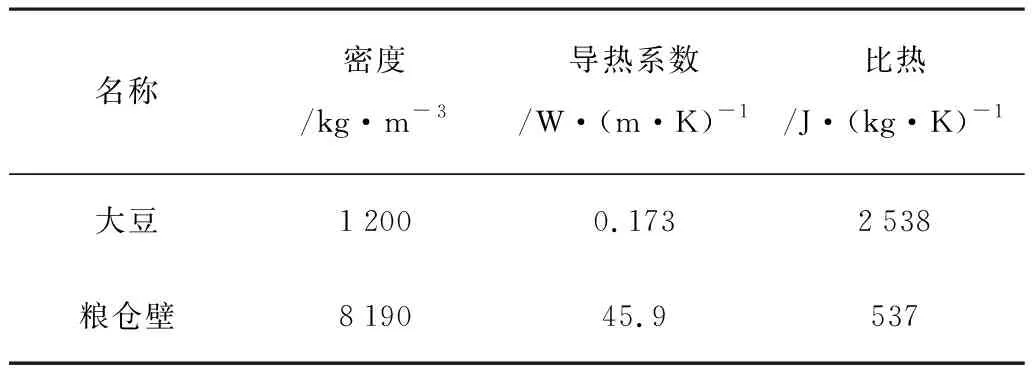
表1 大豆和糧倉的熱物性參數Table 1 The thermophysical parameters of soybean and granary
4 糧食儲藏溫度場有限元模擬分析
4.1 建立有限元數學模型
為了充分利用糧倉分布溫度傳感器網絡測試的實時數據,在建立數學模型時,選取溫度傳感器所在地為模型節點。糧倉有限元三維模型如圖 2 所示。
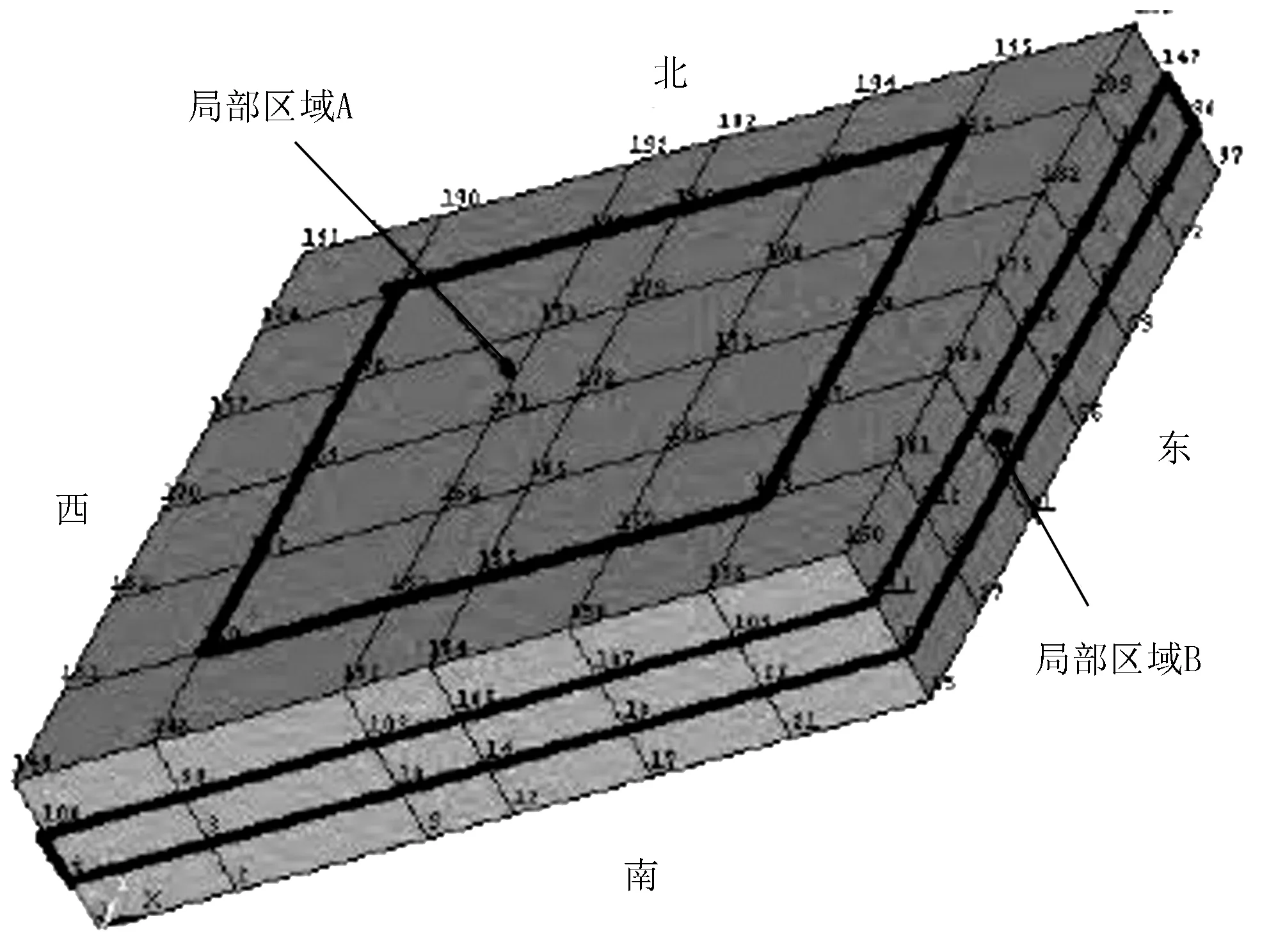
圖2 糧倉有限元三維模型Fig.2 The finite element 3D model of granary
1)確定大豆熱物性參數。在確定糧倉溫度數學模型中,采用表1中大豆的熱物性參數為測試值,即:重力密度為1 200kg/m3,導熱系數為0.173W/(m·K),比熱為2 538J/(kg·K)。
2)設定求解條件。確定糧倉溫度數學模型,進行瞬態溫度場有限元模擬,確定初始和邊界條件也是重要環節。
(1)初始條件:進行糧倉內部瞬態溫度場模擬,首先需要定義各節點溫度初始值,取2015年12月16日00點時刻各溫度傳感器網絡節點溫度值為初始條件。
(2)邊界條件:根據有限元模擬需求,設定第一類邊界條件來邊界條件,即按照指定邊界設定溫度值確定邊界條件,也就是說,邊界上的節點溫度隨著傳感器實際測量時變化。
(3)設定迭代時間和步長:總時間為1年,總共包括 8 760h,步長為12h。
糧倉溫度數學模型建模流程如圖3所示。

圖3 糧倉溫度數學模型建模流程圖Fig.3 The flow chart of mathematical model of granary temperature
4.2 有限元數學模型結果分析
為了更好地分析糧食倉內溫度變化,分別給出了6 000h(2016年8月8日)、8 000h(2016年10月31日)的糧食溫度云圖,如圖4和圖5所示。
從有限元數學模型整體中取出一部分的局部區域可以觀察其內部溫度變化情況。取模型中部區域 (稱為局部A),能夠比較清晰地看出糧倉內部溫度變化情況,局部A 6 000h(2016年8月8日) 計算結果云圖如圖6所示。

圖4 6 000h糧倉溫度云圖Fig.4 The 6 000h granary temperature nephogram
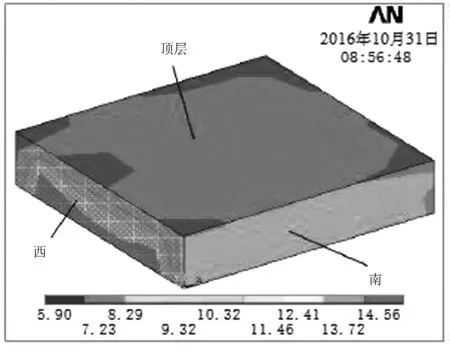
圖5 8 000h糧倉溫度云圖Fig.5 The 8 000h granary temperature nephogram
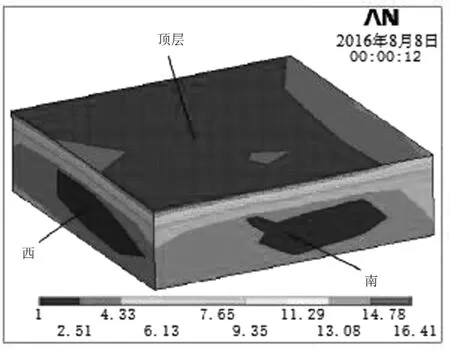
圖6 局部A 6 000h計算結果云圖Fig.6 The local A 6 000h calculation results nephogram
取糧堆的下部分(稱為局部B),可以看出糧倉內部某一截面的溫度變化情況,局部B 8 000h(2016年10月31日) 計算結果云圖如圖7所示。

圖7 局部B 8 000h計算結果云圖Fig.7 The local B 8 000h calculation results nephogram
從上面4幅有限元模擬模型計算結果云圖可以看出:夏天天氣溫度高,糧倉溫度呈現“冷心熱皮”狀態,即糧倉四周溫度高,中心地區溫度低;在糧倉四周溫度變化比較明顯,而在糧倉中心地區溫度變化不明顯,這符合大豆是不良導體的物理性,說明有限元模擬模型計算是真實有效的,采用有限元法求解糧倉溫度是可行的。
5 結論
采用有限元法對大豆糧倉建立了有限元溫度模型,計算模擬出了糧倉1年內的溫度情況。結果表明:采用有限元法可以直觀地觀察糧倉具體時間的溫度分布情況,用有限元法求解糧倉溫度是可行的。模型計算結果表明:外界溫度變化時,糧倉四周溫度變化比較明顯,而在糧倉中心地區溫度變化不太明顯,這符合大豆是不良導體的物理性,也證明有限元模擬模型計算是真實有效的。

