基于模糊PID算法的農機自動轉向系統研究

王茂勵，段 杰，唐勇偉，趙景波，姜 巖

0 引言

我國是一個農業大國，農業人口眾多，但農業發展水平與西方的一些發達國家還有著很大差距。隨著科學技術的迅速發展，現代農業的發展也在日益興起，農業機械化程度對農業發展水平的影響正在日益加深。

發展精準農業是實現現代農業的前提，農機的自動導航系統又是精準農業的重要一步，自動轉向控制系統又是自動導航系統中的關鍵一環。在自動轉向控制系統中，控制算法的選擇、設計及優化的好壞，直接影響農機的作業精度[1-3]。PID控制算法是一種最為常用的控制算法，可以從根本上擺脫系統建模，只需要依據被控對象的一些響應特征來組合控制模塊，控制過程簡單且穩態性好[4-6]。模糊控制亦不依賴于控制模型，而是根據人們的工作經驗，對于被控對象進行簡單的模糊處理，但與此同時影響了控制精度[7-8]。

在此基礎上，將PID算法與模糊控制巧妙地結合起來，能夠互補利弊，會使整個控制系統獲得更加良好的性能，增加系統的靈活性和精確性，可在播種或者收割等工作中加以應用[9]。

1 自動轉向控制系統構成

農機的自動轉向控制系統由導航控制器、轉向控制器、轉向驅動器、農機轉向系統以及轉角測量模塊幾部分組成，如圖1所示。其工作原理為：在農機的導航控制系統中計算出農機的目標轉角后，通過CAN總線將目標轉角的值傳遞給下位機；轉向控制器通過目標轉向角和目前車輪的轉角差值及轉角差值變化率的不同，結合轉向控制算法，控制液壓驅動器來實時調節比例閥的方向和開度，驅動農機轉向系統工作，最終完成農機的自動轉向功能[10]。將農機自動轉向系統的控制過程用二階傳遞函數表示為

(1)

其中，R(s)即目標轉角，Y(s)即轉向角，e、c、d均為待定參數。

2 模糊PID自動轉向控制系統

2.1 PID控制器設計

PID控制算法的表達式為

(2)

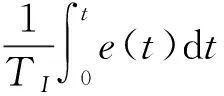
u(k)=

其中，k為采樣次數；u(k)為第k次采樣時輸出的值；e(k)為第k次采樣時輸入的偏差值。由式(3)可以推出

Δu(k)=u(k)-u(k-1)=
KP[e(k)-e(k-1)]+KIe(k)-
KD[e(k)-2e(k-1)+e(k-2)]=
KPΔe(k)+KIe(k)+KD[Δe(k)-Δe(k-1)]

(4)

此時得到的Δu(k)就是增量型PID控制算法的表達式。在采樣中，只要確定了ΔKP、ΔKI、ΔKD這3個參數的值，使用3次的測量偏差從而求出控制量的增量。

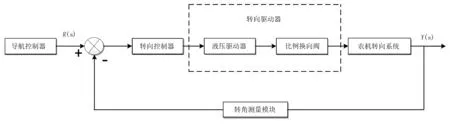
圖1 自動轉向控制系統結構圖Fig.1 Automatic steering control system

2.2 模糊PID控制器設計

模糊PID控制系統的原理就是運用模糊數學的理論和方法，把模糊控制規則以模糊集的形式表示出來，根據被控對象的實際響應情況運用模糊推理，實現對PID參數在不同時間不同狀態下的最佳調整，實現最優控制。系統的結構圖如圖2所示。

圖 2 模糊PID控制系統結構圖Fig.3 Fuzzy PID control system structure diagram

此設計將模糊PID控制器的輸入定為轉向角偏差e(t)和偏差變化率ec(t)，輸出則為模糊控制器經過模糊規則推理得到的ΔKP、ΔKI、ΔKD。系統在線實時改變的參數的值為KP+ΔKP、KI+ΔKI、KD+ΔKD，實現了PID控制算法中參數的自整定環節。此時，參數模糊自整定PID控制的計算量非常小，并且被控對象的動、靜態性能也有所提高。

2.3 模糊控制規則

PID參數自整定的主要思路就是找出PID算法當中的3個參數與轉向角偏差e(t)和偏差變化率ec(t)之間的模糊聯系。當農機在田間行走時，控制器會不斷地檢測e(t)和ec(t)的值，且不斷地對檢測到的值和PID的3個參數進行在線修改，從而滿足在不同環境中的e(t)和ec(t)對PID控制器的不同要求。農機的自動轉向控制系統的響應輸出曲線如圖3所示。

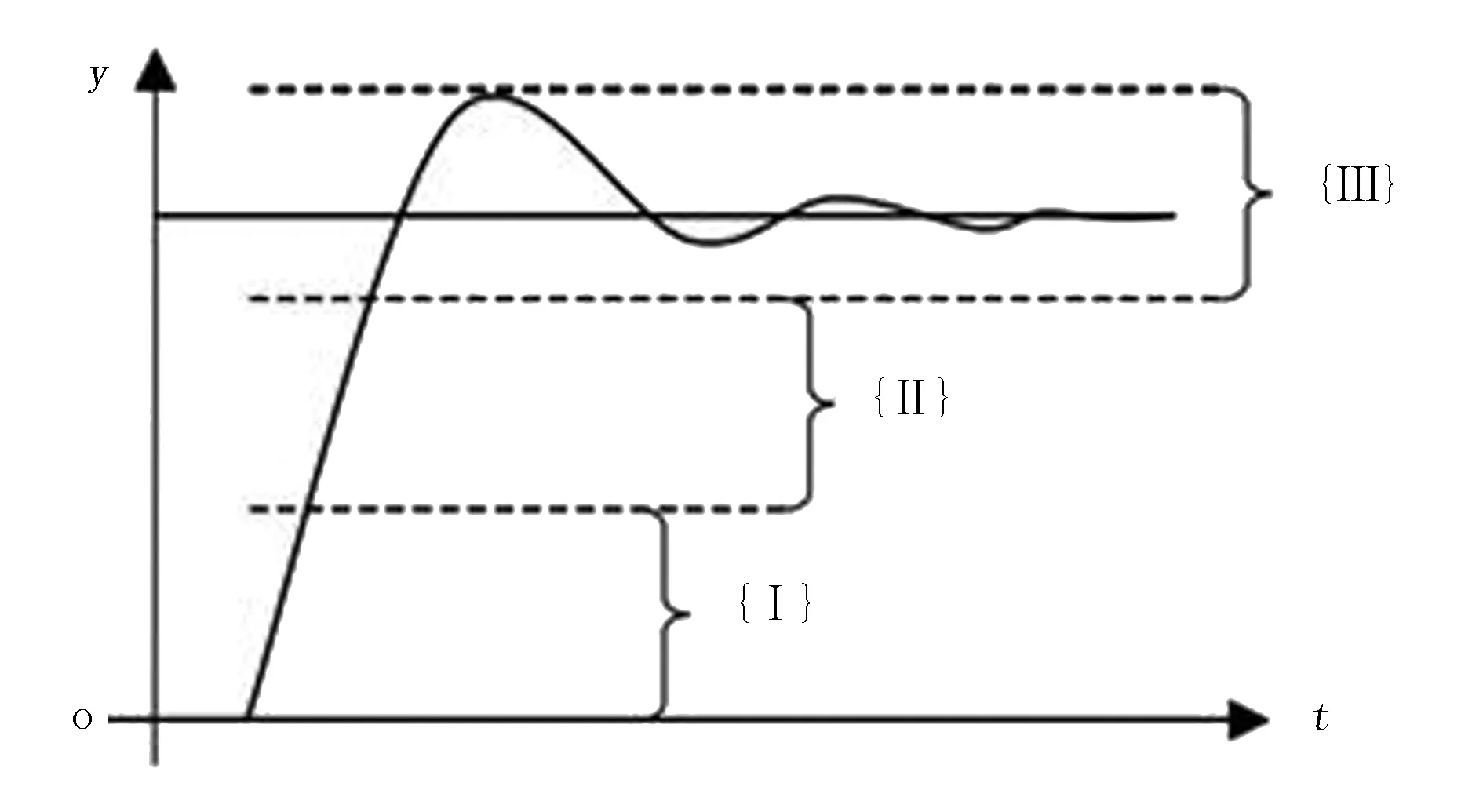
圖 3 系統輸出響應曲線Fig.3 The system outputs the response curve

分析圖3中的響應曲線，可以總結出PID控制算法的3個參數與轉向角偏差e(t)和偏差變化率ec(t)的之間聯系：

1)當輸出響應處于圖中曲線的第 I 階段時，|e(t)|的值較大，為了不讓開始時|e(t)|的值瞬間變大，從而導致微分溢出，應該取較大的KP和較小的KD。這樣還可以提高轉向控制系統的響應速度，還應取KI=0以此來防止積分飽和。

2)當輸出響應處于圖中曲線的第 II 階段時，|e(t)|和|ec(t)|的值都是中等大小，為了減小轉向控制系統的超調，保證步進電機的響應速度，KP、KI和KD的值都不能取得太大，KP的值要取得較小，KI和KD的值要大小適中。

3)當輸出響應處于圖中曲線的第 III 階段時，|e(t)|的值較小，為了使自動轉向系統具有良好的穩態性能，應該增大KP和KI的數值。同時，應該適當的選取KD的值，以此來提高系統的抗干擾能力，其原則是：當|Δe(t)|的值較小時，KD的取值要大一些；當|Δe(t)|值較大時，KD取較小的數值。通常KD和KI的值都要取為中等大小。

根據上述分析可以得出：不確定的系統在常規控制作用下，誤差和誤差變化率e(t)和ec(t)的值越大，系統中的不確定量就越大。那么如果誤差e(t)和誤差變化率ec(t)越小，系統中的不確定量就越小。利用這個e(t)和ec(t)對系統不確定量的估計，進行對PID3個參數KP、KI和KD的調整計算。

在模糊PID控制器的設計過程中，每個輸入輸出量e(t)、ec(t)、KP、KI和KD都需進行相應模糊化的處理。其模糊子集為{NB(負大)，NM(負中)，NS(負小)，ZO(零)，PS(正小)，PB(正大)}，根據農機自動轉向控制系統的特點，各個子集的隸屬函數均選取為高斯型隸屬函數，其中心點分別為{-6，-4，-2，0，2，4，6}，如圖4所示。

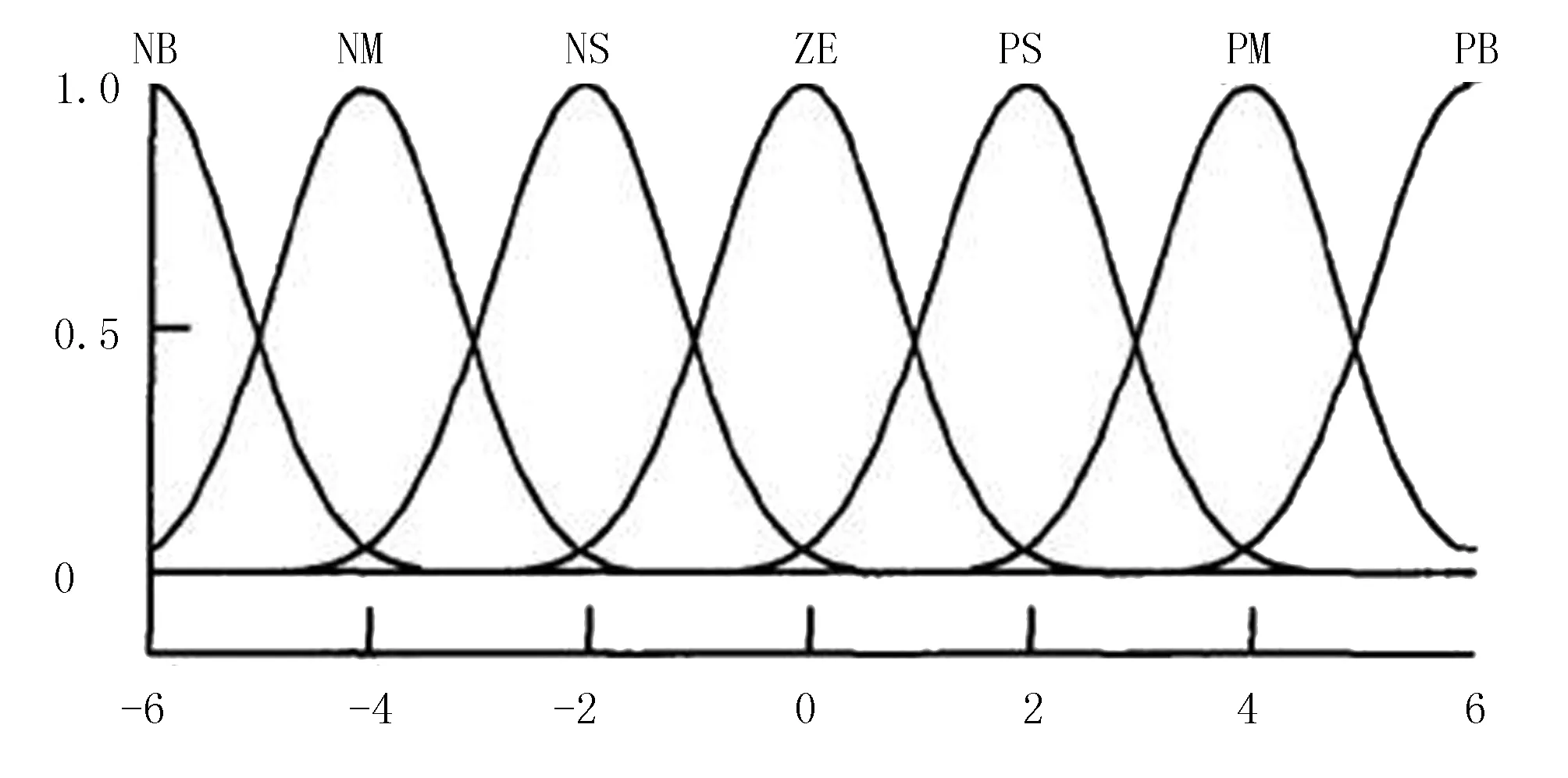
圖4 輸入輸出變量的隸屬度函數Fig.4 The membership function of the input and output variables

根據KP、KI和KD3個參數各自的作用以及它們之間的相互影響，建立KP、KI和KD的模糊控制規則表，如表1～表3所示。

根據KP、KI和KD這3個參數的模糊規則表以及每個模糊子集的隸屬度賦值表，應用模糊規則來推理設計出的PID參數模糊矩陣表，將修正后的參數帶入式(5)～式(7)，來完成對PID參數的在線自矯正。

(5)

(6)

(7)

2.4 解模糊化

通過模糊推理得到的輸出是一個模糊的集合，模糊的量是不可以直接控制對象的。解模糊化的過程就是把通過模糊化得到的模糊集轉化為確定的控制量的過程[9]。運用合理的轉化方法，才能得到準確的控制量去控制被控對象，這里我們采用了重心法，具體方法是先找到模糊隸屬函數曲線與坐標軸的橫軸所圍成面積的重心，然后將這個重心看作成代表點，最后計算出輸出范圍內幾個連續點的重心，即

當輸出變量為離散集時，則為

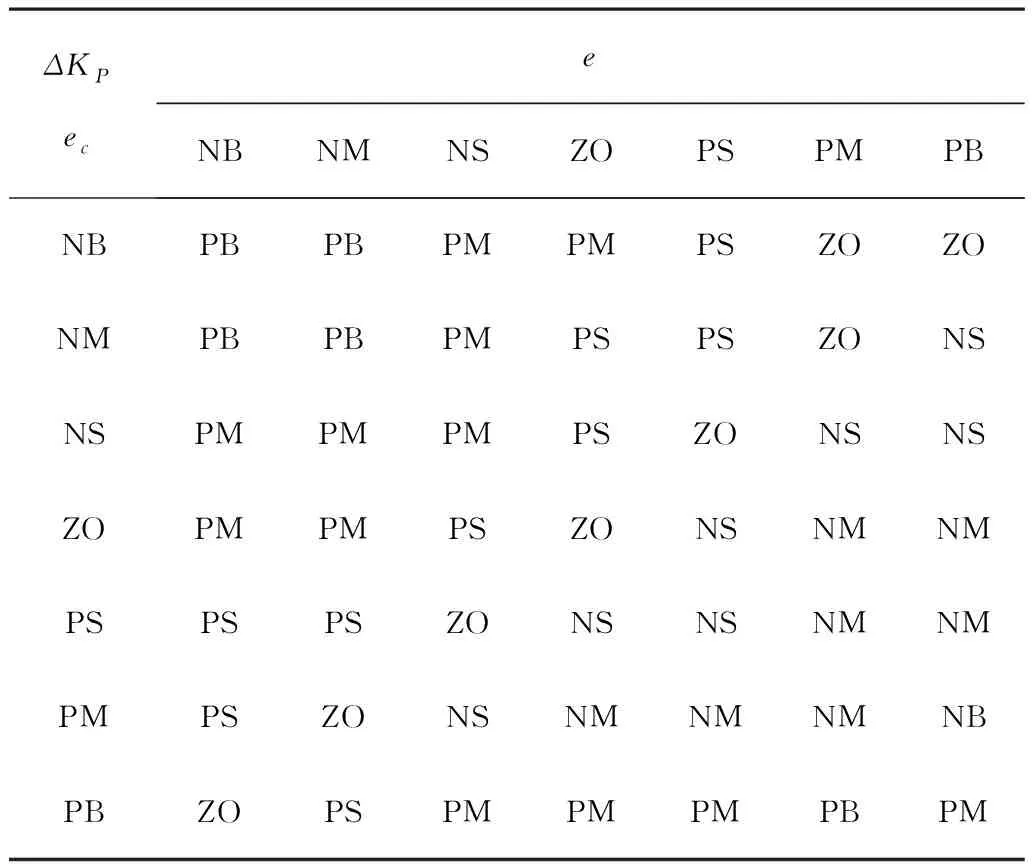
表1 ΔKP模糊控制規則表Table 1 ΔKP fuzzy control rule Table

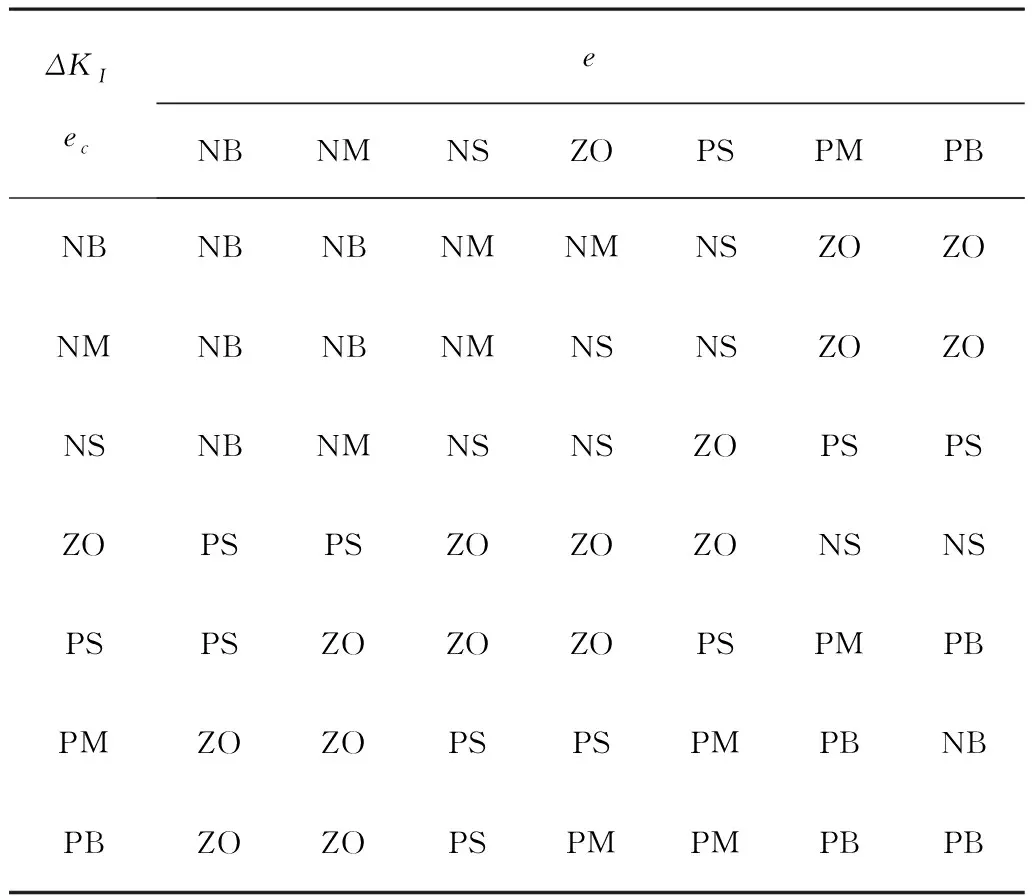
表2 ΔKI模糊控制規則表Table 2 ΔKI fuzzy control rul Table

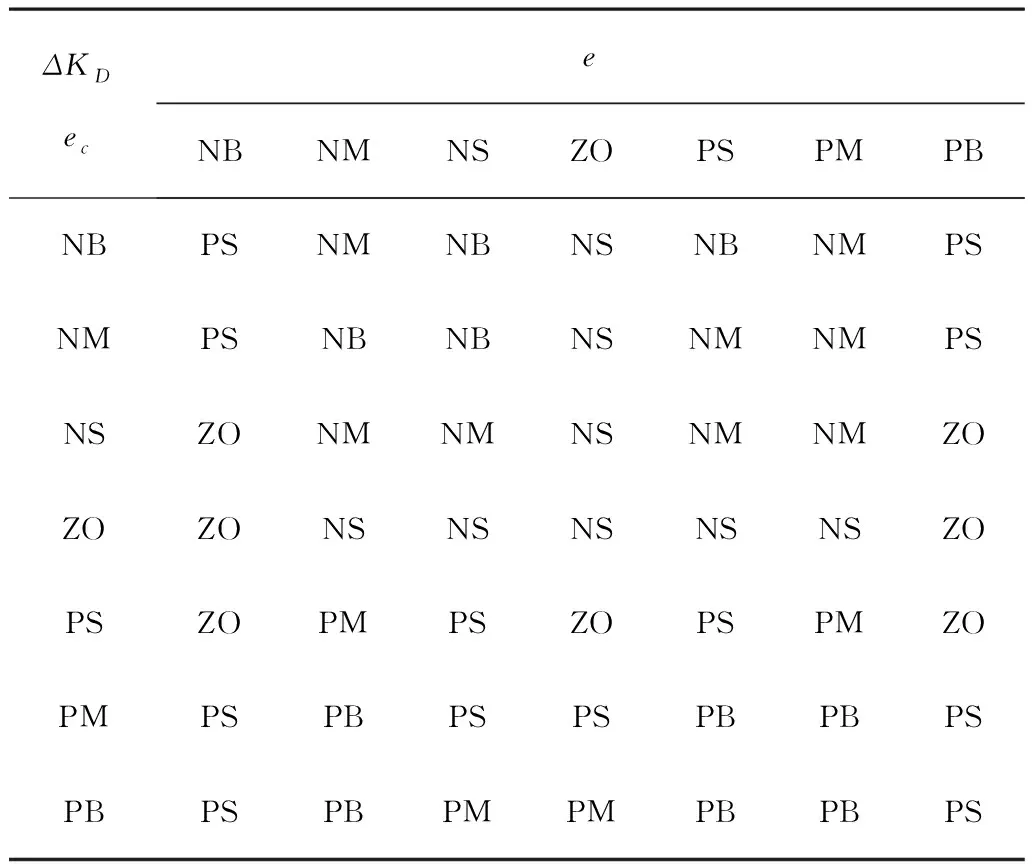
表3 ΔKD模糊控制規則表Table 3 ΔKD fuzzy control rule Table

3 系統試驗與仿真與分析

3.1 系統試驗平臺

系統試驗在山東省臨沂市郯城縣育新合作農場中進行，試驗平臺為東方紅LX1204型拖拉機，如圖5所示。試驗將自動導航控制系統安裝在東方紅拖拉機上，為了在拖拉機轉向時得到精確的數據，將拖拉機的前輪支起騰空，這樣便消除了轉向時與地面產生的摩擦力，從而會更加直觀準確的觀察其特征。

圖5 東方紅LX1204型拖拉機Fig.5 Oriental red LX1204 tractor

3.2 仿真結果與分析

由圖6可以看出：采用模糊PID的控制方法控制農機的轉向會使轉向系統的整個動態性能得到顯著的改善。

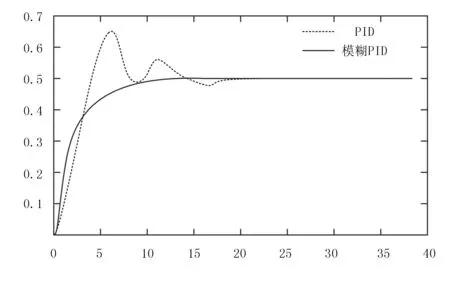
圖6 系統仿真響應曲線Fig.6 System simulation response curve

根據表4可以看出系統的響應時間明顯縮短一倍以上，另外還對轉角進行了實驗。通過上位機向轉向控制器輸入不同的目標轉向角控制指令，可以看出模糊PID控制算法能夠更快的控制拖拉機的自動轉向，能夠更加精確的保證目標角度在±1°以內。

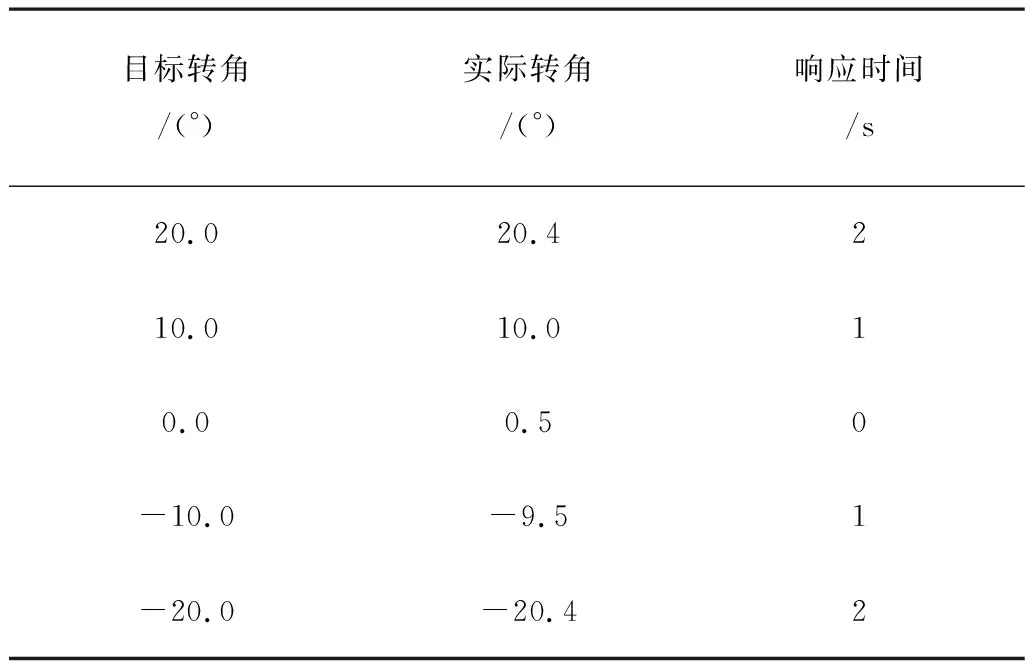
表4 轉角實驗結果Table 4 Corner test results

4 結論

設計了一種基于PID控制算法的模糊PID控制器，并且將其運用到農機的自動轉向控制系統上，較好地結合了兩種算法的優勢使轉向控制系統更加穩定。在實物試驗時，運用東方紅拖拉機進行實物的演示，在MarLab的仿真過程中，分別將在PID控制下和在模糊PID控制下的相應曲線進行對比，在轉角試驗中輸入不同的目標值對農機的轉角及響應時間進行記錄和分析。結果表明：此控制方法能夠在滿足農機控制要求的基礎上將其優化，具有更好的快速性和準確性，響應時間更短，穩態誤差更小，是一種可靠且優良的控制方法。