勻質三角薄板轉動慣量的計算

葉 松，許明坤，張自鋒

（巢湖學院 機械與電子工程學院，安徽 合肥 238000）

轉動慣量是研究剛體運動所必需的基本物理量之一.勻質三角薄板是重要的平面結構，它可以和弓形等結構構成工程中常用的復雜剛體結構[1,2].由于轉動慣量的可疊加性，討論勻質三角薄板的轉動慣量對分析復雜剛體結構的轉動慣量非常有用.文獻[3]給出勻質三角薄板對經過質心的任意轉軸的轉動慣量，但計算過程繁瑣.文獻[4-7]推導了三角形框剛體的轉動慣量，但是該結論不能直接推廣到勻質三角薄板剛體.在工程實踐中平面剛體定軸轉動的Z轉軸一般都是垂直剛體平面，因此得到適用勻質三角薄板質心的轉動慣量的簡潔公式是有必要的.本文基于平行軸定理和垂直軸定理簡捷地推導出勻質三角薄板剛體的質心轉動慣量公式.

1 勻質三角薄板對坐標軸的轉動慣量

已知垂直軸定理對給定Z軸的轉動慣量與在薄剛體平面的X軸和Y軸選取無關.因此為了使討論過程簡潔，設勻質三角薄板底邊AB在X軸，高OC在Y軸，頂點A、B和C的坐標如圖1所示.

圖1 計算勻質三角薄板對X軸轉動慣量時的質量微元示意

首先討論勻質三角薄板對X軸的轉動慣量.取細桿微元位于[h',h'+dh']，長為L'，其對X軸的轉動慣量微元是：

(1)式中σ是勻質三角薄板的面密度，其中：

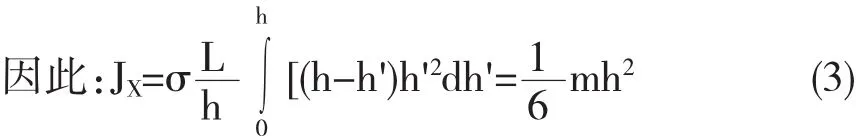
式(2)和(3)中L和h是AB和OC的長度.

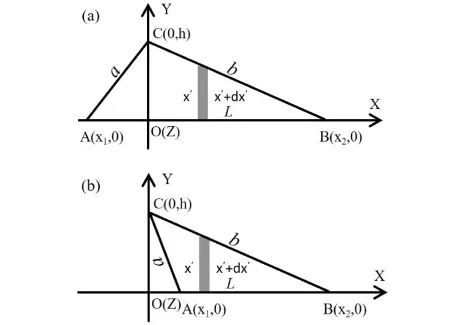
圖2 計算勻質三角薄板對Y軸轉動慣量時的質量微元示意

其次討論勻質三角薄板對Y軸的轉動慣量.如圖2所示是勻質三角薄板的A、B頂點X軸坐標值滿足x1x2≤0和x1x2＞0的兩類情形.勻質三角薄板對Y軸的轉動慣量，對圖2(a)所示情形，等于△AOC和△BOC對Y軸的轉動慣量之和；對圖2(b)所示情形，等于△BOC和△AOC對Y軸的轉動慣量之差.由公式（3）得到圖2(a)和2(b)的轉動慣量均為：

最后由垂直軸定理可以得到勻質三角薄板對Y軸的轉動慣量：

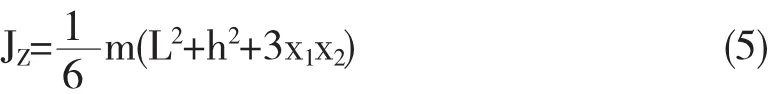
2 勻質三角薄板對質心的轉動慣量

勻質三角薄板對質心的轉動慣量可以運用平行軸定理計算.如圖3所示，G是勻質三角薄板的質心，其坐標為和 GZ'是勻質三角薄板質心G的主軸，分別平行X軸、Y軸和Z軸.

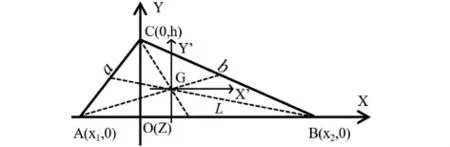
圖3 計算勻質三角薄板過質心定軸轉動慣量的示意

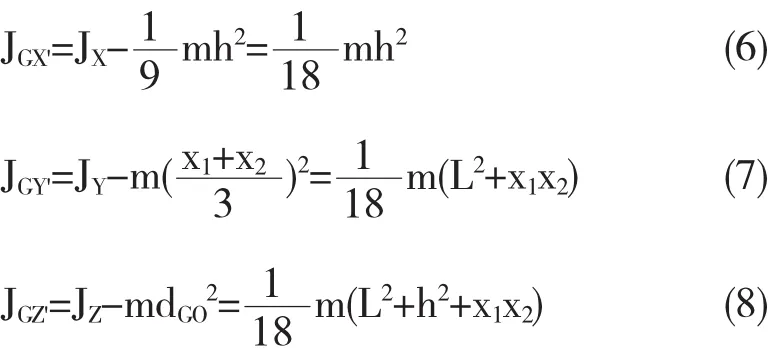
（8）式中是質心到坐標原點的距離.

在工程實踐中，三角形剛體的邊長是易于測量的，因此得到用邊長表示的轉動慣量是有必要的.記三角形邊長分別為a、b、L，(6)-(8)式可以表示為：

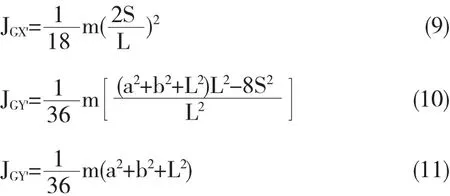
(9)式中

（11）式與文獻[3]的推論一致.

3 結論

通過求解特定坐標系中勻質三角薄板對邊長的轉動慣量，結合平行軸定理和垂直軸定理，推導了勻質三角薄板對質心轉動軸的轉動慣量公式.求解思路清晰，過程簡捷，有助于提高學生對平行軸定理和轉動軸定理的理解和應用，對拓寬學生計算剛體轉動慣量的數理思路有一定引導作用.