求極限方法在數學分析中的應用分析
王 健
(曲阜師范大學,山東 曲阜 273165)
一、極限思想的產生和發展
(一)極限思想的由來
極限思想是經過古代人們長期研究數學從而不斷形成的一種數學思想。極限思想是由一種最原始的極限思想逐漸衍生的。查閱相關資料可以知道,古希臘人的窮竭法正是運用的極限思想,
(二)極限思想的發展
極限思想的發展有賴于微積分的發展。隨著資本主義的不斷發展,生產力得到了很大的提高,之前運用的初等數學已經不能滿足平常的記錄工作,因此必須加快數學方法的研究。最剛開始是牛頓和萊布尼茨以無窮小概念為基礎建立微積分的思想。雖然在發展的過程中遇到了很多難以解決的問題,但是經過不懈的努力,他們在后期都接受了極限思想。
(三)極限思想的完善
極限思想的完善離不開微積分的發展。通過研究微積分,從而掌握極性思想。在十九世紀的時候,法國數學家柯西在總結前人經驗的基礎上,之后再不斷探索,得出了無窮小的概念。
二、常見的極限方法
(一)利用重要極限求函數極限
以下是兩個常見的極限,在平常的練習中也可以直接運用。
它們分別是一元函數兩個重要極限的推廣。第一個極限可以把x當做一個整體進行求解。第二個極限求解時牢記“外大內小,內外互倒”的解題思想。對函數進行適當的變形是十分關鍵的,需要根據函數的特征來判斷從而進行函數變形。
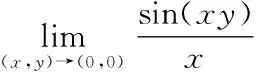
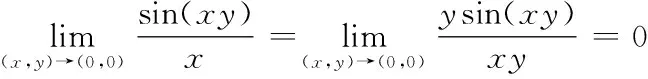
根據極限的推導可以很容易求出要求解的問題。
(二)利用洛必達法則求極限
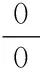
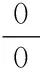
定理1若函數f(x)和函數g(x)滿足
(ii)在點x0的某空心鄰域Uo(x0)內兩者都可導,且g′(x)≠0;

則
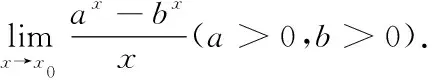
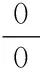
在做題的時候先研究所求極限的類型,確定采用哪一種極限方法更好,這樣可以減少做題的彎路,而且準確率也更高。長期的接觸采用極性方法解決問題,對個人的數學思想的提高會有很大的幫助。
三、建立概念的極限思想
極限的思想方法一直貫穿于整個數學分析的課程當中。掌握數學分析的概念必須先從極限思想開始。通過學習與極限思想有關的連續函數、導數、定積分、級數的斂散性等相關數學知識,慢慢的掌握與極限有關的內容。我們需要了解的是函數在進行點連續的定義時,自變量有增量時,函數值的增量趨近于零。如果是對于點導數定義,函數值的增量與自變量的增量之比就是所求的極限值。
四、解決問題的極限思想
極限思想方法是解決數學問題的一種必不可少的數學方法。數學分析可以很巧妙地解決各類問題,正是運用了極限思想。當我們需要確定某一個量時,一般來講我們先確定的是它的近似值而不是量本身,確定的近似值野獸一連串越來越準確地近似值,通過考察近似值的趨向,最終確定量的具體值。這正是極性思想的應用。
五、結語
極限的思想方法是人們在日常的學習過程中慢慢形成的,從近似到精確,從量變到質變的轉變,它是事物轉變過程中的一個重要環節,同時也是數學分析中需要重點掌握的內容。只有認真的去學習和探索,才能更好的掌握極限思想,從而提高數學分析的能力。

