案例驅動下的分類與預測課程教學方法研究
方 歡,方賢文,郭 娟,陳小奎
(安徽理工大學數學與大數據學院,安徽淮南 232001)
近年來,隨著大數據技術應用的深入,開設“數據科學與大數據技術”(專業代碼:080910T)以及在已有專業的基礎上增設“數據分析與挖掘”專業方向的本科院校越來越多,而在市場招聘中,對于數據分析與挖掘類人才的能力與要求也各有不同。根據領英人才報告,相關的大數據人才需求可以分為幾個層次,具體如表1所示。從表1的崗位和技術能力要求可以看出,雖然大數據分析師是目前的亟需人才,但是這個崗位對專業技術能力的要求也較高。因此,在本科院校中研究如何展開數據分析師相關課程的教學工作十分必要。

表1 市場對大數據人才的需求層次
以筆者所在學校為例,其目前在應用統計學、信息與計算科學兩個理科專業,都開設有“數據分析與處理”“數據挖掘技術”以及“Python程序設計方法”等課程[1-3],用以支撐這兩個專業學生在數據分析方向的就業,這也進一步促進了有關數據挖掘相關課程的教學研究[4-7]。本文針對“數據挖掘技術”課程中“分類與預測”內容的教學方法進行深入探討,結合教學實踐,闡述在案例驅動的條件下使用Python程序對分類與預測方法進行教學,并給出相關的實驗設計方案。
1 分類與預測的總體教學方案設計
1.1 經典的分類與預測方法
在“數據挖掘技術”課程中,主要介紹以下六種分類與預測方法:(1)基于決策樹的分類預測方法;(2)基于條件規則的分類預測方法;(3)基于神經網絡的分類預測方法;(4)基于支持向量機的分類預測方法;(5)基于樸素貝葉斯及貝葉斯信念網絡的分類預測方法;(6)基于記憶的推理分類預測方法。
在這些方法中,基于決策樹的方法、樸素貝葉斯方法以及基于條件規則的方法不需要太多的預備知識,只需要掌握經典的概率論方法即可,因此在本科生教學時選擇這三種方法為主要講解內容,調整后的分類預測方法教學內容如下:(1)信息熵理論、信息的不確定性理論;(2)決策樹的概念;(3)ID3分類預測算法;(4)規則條件系統以及決策樹與條件規則系統的轉換;(5)樸素貝葉斯分類預測算法;(6)分類預測算法的評價。
1.2 背景案例
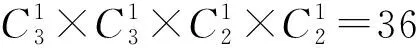
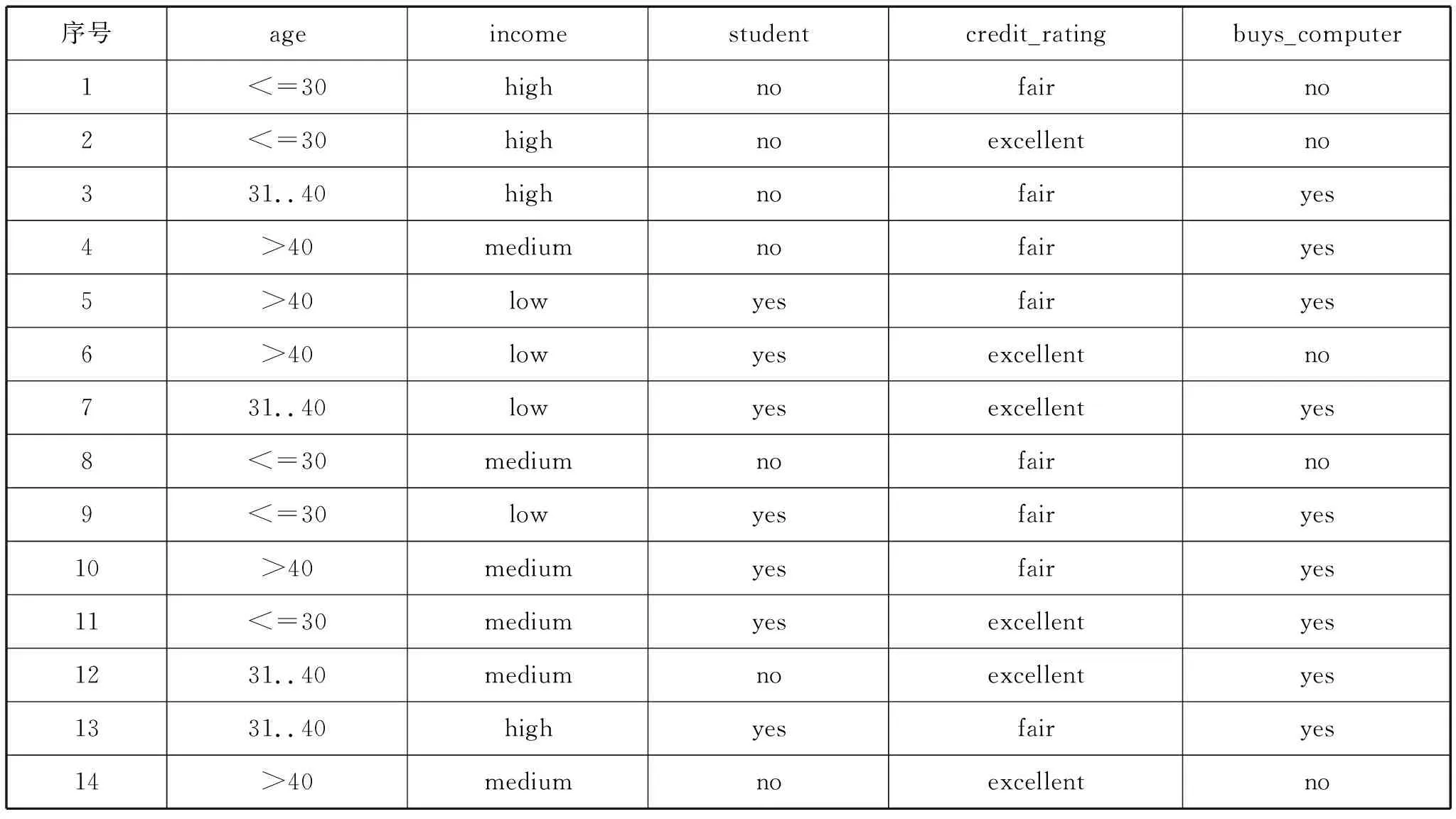
表2 采集的案例數據集

表3 需要分類預測的數據集
2 基于信息熵的ID3算法
2.1 信息熵與信息的不確定性
2.1.1 基于古典概率模型的信息熵
例 有32個足球隊比賽,每個隊實力相當,每一個隊勝出的概率都是1/32,那么要猜對哪個足球隊勝出非常困難,此時熵H(X)=5。試想如果32個隊中有1個是AC米蘭隊,另外31個隊是安理信計1班、2班、…、31班,那么幾乎只有一個可能,即AC米蘭隊勝利的概率是100%,其他球隊的獲勝概率都為0,此時這個系統的熵就是H(X)=0。
2.1.2 熵的性質
(1)有序的系統,熵為0;(2)熵也可以作為一個系統的混亂程度的標準,系統越混亂,熵越大。因此,熵可以作為衡量信息量大小的度量標準之一。
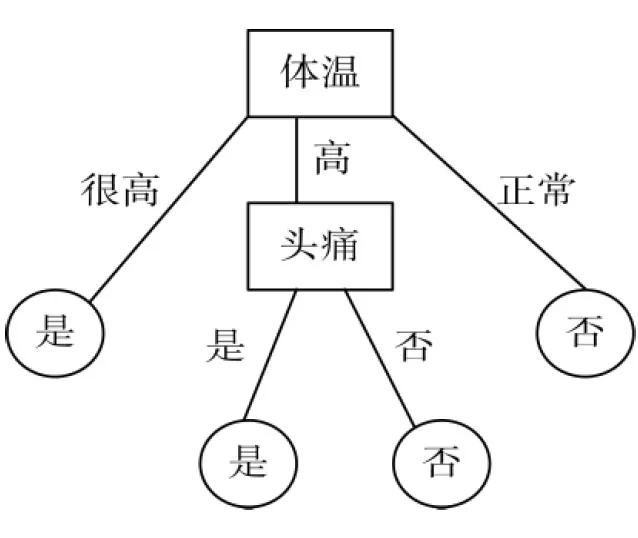
2.2 決策樹的基本概念
決策樹是樣本知識的一種表現形式,主要由三類結點組成:決策結點、分支以及葉子結點,其中決策結點由樣本屬性構成,而分支則來源于樣本屬性的取值,葉子結點為分類標簽值。圖1給出了一個流感問題描述的決策樹模型,方形為決策結點,圓形是葉子結點,而邊上的標注為屬性分支。
2.3 基于ID3算法的決策樹構造
2.3.1 決策樹構造思路
使用貪心法來選擇具有最高信息增益的屬性作為當前計算的分裂屬性,因此一顆ID3決策樹一定滿足以下三個條件:(1)決策樹的根結點是所有樣本中信息量最大的屬性;(2)樹的中間結點是以該結點為根的子樹所包含的樣本子集中信息量最大的屬性;(3)決策樹的葉子結點是樣本的類別值。
2.3.2 決策樹的計算過程

2.3.3 算法示例
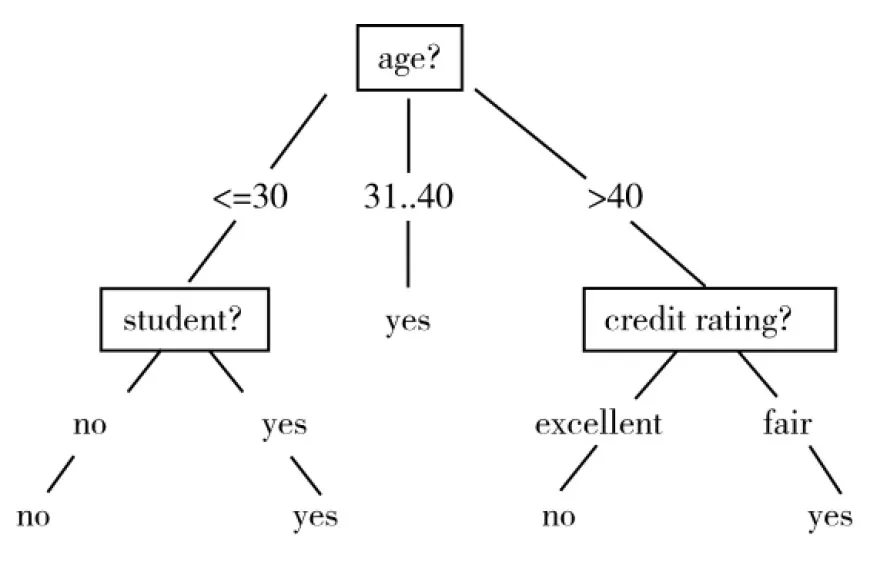
根據決策樹構造算法,對表2的樣本數據進行計算,可以得到如圖2所示的決策樹模型。
3 決策樹模型向條件規則系統的轉換方法
根據決策樹模型,可以很容易得到相關樣本的條件規則系統。轉換規則如下:從樹根開始,選擇任意一條可以達到葉子結點的路徑,將分裂屬性及其對應的分支條件結合起來,并使用合取條件進行條件復合,即可得到一條規則,重復這個過程直至所有的路徑都被遍歷。
根據這個思路,圖2的決策樹表達成條件規則系統,如下所示:
(1)age<=30 and student=’no’ then buys_computer=’no’;
(2)age<=30 and student=’yes’ then buys_computer=’yes’;
(3)age in 31..40 then buys_computer=’yes’;
(4)age>40 and credit_rating=’excellent’ then buys_computer=’no’;
(5)age>40 and credit_rating=’fair’ then buys_computer=’yes’.
由此,這五條規則構成了表2樣本的條件規則系統。
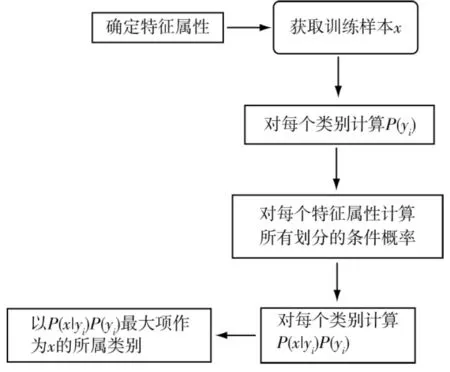
4 基于樸素貝葉斯算法的分類預測方法
4.1 樸素貝葉斯算法的基本思想
所謂的“樸素”是指樣本的屬性特征相互獨立,在此條件下才可以進行樸素貝葉斯的分類預測算法。
樸素貝葉斯分類的思想如下:
step1 設x={a1,a2,…,am}為一個待分類項,而每個ai為x的一個特征屬性;
step2 有類別集合C={y1,y2,…,yn};


樸素貝葉斯分類決策算法的決策過程如圖3所示。
4.2 樸素貝葉斯算法演示
以表2的樣本數據為例,假設待分類數據x為x={age=”<=30”,income=”medium”,student=”yes”,credit_rating=”fair”},表2的樣本可以分為兩類:Class y1:buys_computer=“yes”和Class y2:buys_computer=“no”。
計算過程如下:
step1 計算每個類的先驗概率P(yi):P(y1)=9/14,P(y2)=5/14;
step2 計算每個特征屬性對于每個類別的條件概率:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)



step5 結論
對于樣本x,樸素貝葉斯分類預測buys_computer=”yes”。
5 基于Python的分類預測程序實現方法
Python程序是目前數據挖掘與機器學習最常用的一門設計語言,使用Python對上述的ID3以及樸素貝葉斯算法進行使用大致有兩種途徑:(1)可以根據本文給出的算法思路進行個性化設計,將算法過程用Python進行展示;(2)通過調用Python中的scikit-learn包庫來進行算法調用。前者耗時較大,后者使用比較簡單。本文主要講解后者的調用方法。
5.1 ID3算法的Python包庫調用方法
在scikit-learn包庫中存在decision-tree-id3模型,可以使用如下格式進行調用(其中load_breast_cancer為調用的數據集名稱):
>>>from sklearn.datasets import load_breast_cancer
>>>from id3 import Id3Estimator
>>>from id3 import export_graphviz
>>>bunch = load_breast_cancer()
>>>estimator = Id3Estimator()
>>>estimator.fit(bunch.data, bunch.target)
>>>export_graphviz(estimator.tree_, ’tree.dot’, bunch.feature_names)
5.2 scikit-learn中樸素貝葉斯模型的調用方法
在scikit-learn中存在三種不同屬性的樸素貝葉斯模型。(1)高斯分布模型:假定屬性(特征)服從整體分布;(2)多項式模型:用于離散值模型,比如文本分類與挖掘問題;(3)伯努利模型:在這種情形下,特征只能表述為0(沒出現)或1(出現過)。
其各自的調用方式分別為:
>>>fromsklearn import metrics
>>>fromsklearn.naive_bayes import GaussianNB
>>>fromsklearn.naive_bayes import MultinomialNB
>>>fromsklearn.naive_bayes import BernoulliNB
以其中的GaussianNB模型為例,下面給出一組GaussianNB的分類預測算法實現過程:
>>>model= GaussianNB()
>>> start_time= time.time()
>>>model.fit(X,y)
>>>print(’training took %fs!’%(time.time()-start_time))
>>>print(model)
>>>expected= y
>>>predicted= model.predict(X)
>>>print(metrics.classification_report(expected,predicted))
>>>print(metrics.confusion_matrix(expected,predicted))
6 結語
在目前大數據背景下,我們把分類和預測統稱為推測。分類就是應用已知的一些屬性數據去推測一個未知的離散型的屬性數據,而這個被推測的屬性數據的可取值是預先定義的。想要很好地實現這種推測,就需要事先在已知的一些屬性和未知的離散型屬性之間建立一個有效的模型,即分類模型。本文主要講解了應用古典概率模型就可以計算的ID3決策樹模型、樸素貝葉斯算法模型。除此之外,還有很多可以應用的數學模型,比如神經網絡、logistic回歸、支持向量機等。這些數學模型可能比較難,如何將這些數學模型與編程語言結合起來是一件非常困難的事情,需要教師不斷地應用各種案例進行引導,加深學生的理解。另外,在實際教學過程中,還可引入一些案例讓學生動手實踐,使學生對分類預測方法有更深刻的理解,提高學生的實踐動手能力。

