中考課題學習型試題

文 /鄧革周

課題學習型試題常以幾何圖形為題材，或以數學問題為背景，通過對相關問題的描述或逐步觀察、操作、探究，進而發現問題，解決問題.中考課題學習型試題常見的有三種：操作發現型、猜想論證型、類比探究型.

一、操作發現型

例1【操作發現】如圖1，在邊長為1個單位長度的小正方形組成的網格中，△ABC的三個頂點均在格點上．

（1）請按要求畫圖：將△ABC繞點A按順時針方向旋轉90°，點B的對應點為B′，點C的對應點為C′，連接BB′；

【問題解決】

如圖2，在等邊三角形ABC中，AC=7，點P在△ABC內，且∠APC=90°，∠BPC=120°，求△APC的面積．

小明同學通過觀察、分析、思考，對上述問題形成了如下想法：

想法一：將△APC繞點A按順時針方向旋轉60°，得到△AP′B，連接PP′，尋找PA，PB，PC三條線段之間的數量關系；

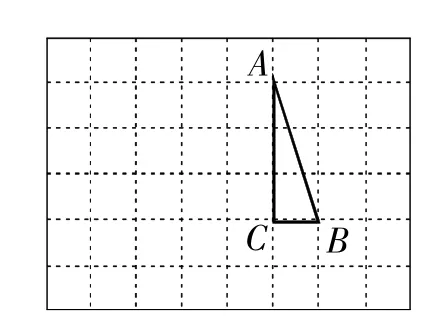
圖1

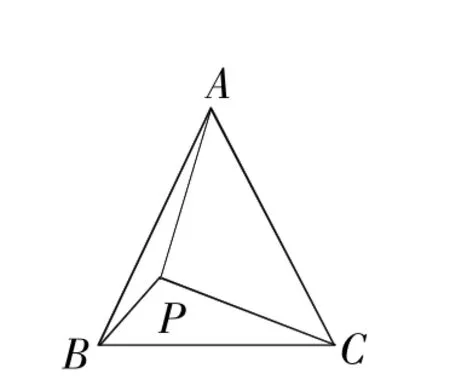
圖2

想法二：將△APB繞點A按逆時針方向旋轉60°，得到△AP′C′，連接PP′，尋找PA，PB，PC三條線段之間的數量關系.

……

請參考小明同學的想法，完成該問題的解答過程.（一種方法即可）【靈活運用】

如圖3，在四邊形ABCD中，AE⊥BC，垂足為E，∠BAE=∠ADC，BE=CE=2，CD=5，AD=kAB（k為常數），求BD的長（用含k的式子表示

圖3

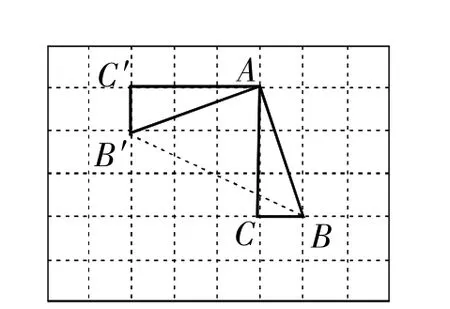
圖4

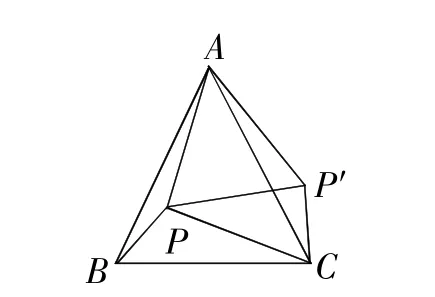
圖5

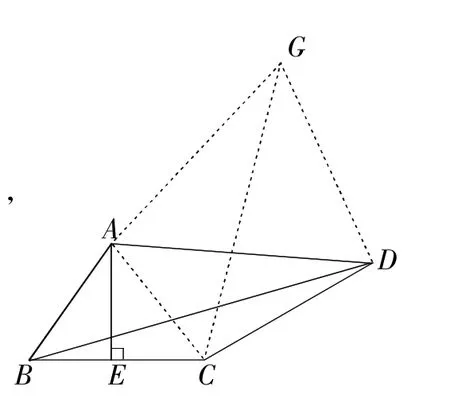
圖6

解：【操作發現】（1）如圖4所示，△AB′C′即為所求.

（2）連接BB′，

∵AB=AB′，∠B′AB=90°，∴∠AB′B=45°.

【問題解決】如圖5，

將△APB繞點A按逆時針方向旋轉60°，得到△AP′C′，

∴△APP′是等邊三角形，

∠AP′C=∠APB=360°-90°-120°=150°，

∴∠PP′C=∠AP′C-∠AP′P=150°-60°=90°，

∠P′PC=∠APC-∠APP′=30°，

∵∠APC=90°，∴AP2＋PC2=AC2，即

【靈活運用】如圖6，∵AE⊥BC，BE=EC，∴ AB=AC，

將△ABD繞點A逆時針旋轉得到△ACG，連接DG，則BD=CG，

∵∠BAD=∠CAG，∴∠BAC=∠DAG.

∵AB=AC，AD=AG，∴∠ABC=∠ACB=∠ADG=∠AGD，

∴△ABC∽△ADG.

∵AD=kAB，∴DG=kBC=4k.

∵∠BAE+∠ABC＝90°，∠BAE=∠ADC，∴∠ADG+∠ADC=90°

二、類比探究型

例2問題背景：已知∠EDF的頂點D在△ABC的邊AB所在直線上（不與A，B重合），DE交AC所在直線于點M，DF交BC所在直線于點N，記△ADM的面積為S1，△BND的面積為S2．

（1）初步嘗試：如圖7，當△ABC是等邊三角形，AB=6，∠EDF=∠A，且DE∥BC，AD=2時，則

（2）類比探究：在（1）的條件下，先將點D沿AB平移，使AD=4，再將∠EDF繞點D旋轉至如圖8 所示位置，求S1·S2的值；

（3）延伸拓展：當△ABC是等腰三角形時，設∠B=∠A=∠EDF=α．

（i）如圖9，當點D在線段AB上運動時，設AD=a，BD=b，求S1·S2的表達式（結果用a，b和α的三角函數表示）；

（ii）如圖10，當點D在BA的延長線上運動時，設AD=a，BD=b，直接寫出S1·S2的表達式（不必寫出解答過程）．

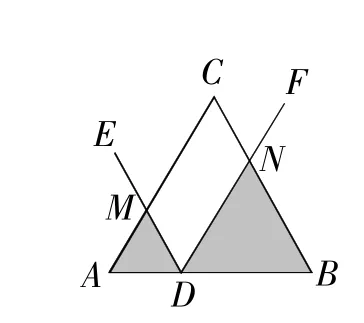
圖7

圖8

圖9

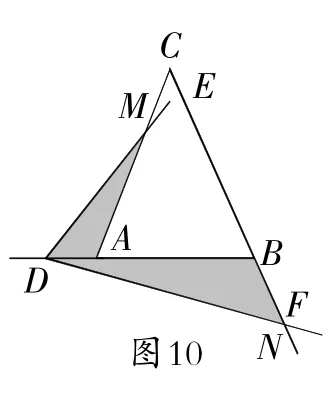
圖10

解：（1）如圖7，∵△ABC是等邊三角形，

∴AB=CB=AC=6，∠A=∠B=60°，

∵DE∥BC，∠EDF=60°，∴∠BND=∠EDF=60°，

∴∠BDN=∠ADM=60°，∴△ADM，△BDN都是等邊三角形，

（2）如圖8，設AM=x，BN=y.

∵∠MDB=∠MDN+∠NDB=∠A+∠AMD，∠MDN=∠A，

∴∠AMD=∠NDB，

∵S1＝

∴S1·

（3）（i）如圖9，設AM=x，BN=y，

同法可證△AMD∽△BDN，可得xy=ab，

（ii）如圖10，設AM=x，BN=y，

同法可證△AMD∽△BDN，可得xy=ab，

∵S1=（ab）2sin2α．

三、猜想論證型

例 3 如圖11，在Rt△ABC中，∠A=90°，AB=AC，點D，E分別在邊AB，AC上，AD=AE，連接DC，點M，P，N分別為DE，DC，BC的中點.

（2）探究證明：把△ADE繞點A逆時針方向旋轉到圖12的位置，連接MN，BD，CE，判斷△PMN的形狀，并說明理由；

（3）拓展延伸：把△ADE繞點A在平面內自由旋轉，若AD=4，AB=10，請直接寫出△PMN面積的最大值.

解：（1）∵點M，P，N是DE，CD，BC的中點，

∵AB=AC，AD=AE，∴BD=CE，∴PM=PN.

∵PN∥BD，∴∠DPN=∠ADC.

∵PM∥CE，∴∠DPM=∠DCA.

∵∠BAC=90°，∴∠ADC+∠ACD=90°，

∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM⊥PN，

故答案為：PM=PN，PM⊥PN.

（2）由旋轉知，∠BAD=∠CAE，

∵AB=AC，AD=AE，∴△ABD≌△ACE，

∴∠ABD=∠ACE，BD=CE，

圖11

圖12

∴PM=PN，∴△PMN是等腰三角形，

同（1）的方法得，∠DPM=∠DCE，∠PNC=∠DBC，

∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，

∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC

=∠ACB+∠ACE+∠DBC

=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC=90°，

∴△PMN是等腰直角三角形.

圖13

∴PM最大時，△PMN面積最大，∴點D在BA的延長線上，

∴BD=AB+AD=14，∴PM=7.

∴S△PMN最大=