不含特殊子式的符號圖的選擇數

宮 辰，武麗芳，劉維嬋，張 欣

GONG Chen,WU Lifang,LIU Weichan,ZHANG Xin

西安電子科技大學 數學與統計學院，西安 710071

School of Mathematics and Statistics,Xidian University,Xi’an 710071,China

1 引言

設G是一個有限的、無向的簡單圖。分別用V(G)與E(G)代表圖G的點集合與邊集合。對于圖G的每條邊e，定義其符號σ(e)為 +1或者-1，由此得到的圖稱為符號圖，記為(G,σ)。對于符號圖(G,σ)中的邊e，如果σ(e)=+1，則稱其為正邊；如果σ(e)=-1，則稱其為負邊。符號圖的概念最初是由Harary[1]于1955年在一篇數學文章中提出的，之后又被Cartwright與Harary[2]用于社會心理學的研究。例如，在人際關系網中用點代表自然人，如果兩個人之間是朋友關系，則將對應這兩個人的點用一條正邊連接；反之，如果兩個人之間是敵對關系，則將對應這兩個人的點用一條負邊連接。繼而，可以通過建立符號圖的數學模型來分析人際關系網中的一系列問題，如穩定性、社團劃分問題等。

事實上，網絡的社團劃分問題的研究可以歸結于圖的染色問題[3-4]。1982年，Zaslavsky[5-7]首次定義了符號圖的染色。設(G,σ)是一個符號圖，c是從點集V(G)到數集{-k,-(k-1),…,-1,0,1,…,(k-1),k}的映射，其對于圖G的任何一條邊uv滿足：

（1）若σ(uv)=+1，則c(u)≠c(v)；

（2）若σ(uv)=-1，則c(u)≠-c(v)。

該映射c稱為圖(G,σ)的具有k個顏色的或者具有2k+1個符號顏色的符號點染色。

2016 年 ，Má?ajová、Raspaud 與 ?koviera[8]指 出Zaslavsky的上述定義存在缺陷，即該定義不能直接從無符號圖的定義直接轉換過來。為了克服這個缺陷，Má?ajová等結合Zaslavsky的定義，重新給出了符號圖的符號點染色的定義。

設Mn為整數集的一個子集，當n=2k時，令Mn={±1,±2,…,±k}；當n=2k+1 時 ，令Mn={0,±1,±2,…,±k}。如果一個從點集V(G)到數集Mn的映射c對于圖G的任何一條邊uv滿足c(u)≠σ(uv)c(v)，則稱映射c為符號圖(G,σ)的符號n-點染色。使得符號圖(G,σ)具有符號n-點染色的最小整數n，稱為符號圖(G,σ)的符號點色數，記為χ(G,σ)。

2016年，Jin、Kang與Steffen[9]提出了符號圖的列表染色的概念。設(G,σ)是一個符號圖，對于其每個點v賦予一個顏色列表L(v)??。符號圖(G,σ)的L-點染色是其一個點染色c，其滿足：

（1）對于任何點v∈V(G)，都有c(v)∈L(v)；

（2）對于任何邊uv∈E(G)，都有c(u)≠σ(uv)c(v)。

如果符號圖(G,σ)具有L-點染色，則稱其為L-點染色。如果符號圖(G,σ)上的顏色列表L對于任何點v∈V(G)都有| |L(v)=k，則稱該列表L為k-列表。如果對于任何一個k-列表L，符號圖(G,σ)都具有L-點染色，則稱其是k-點可選的。使得符號圖(G,σ)是k-點可選的最小整數k稱為符號圖(G,σ)的選擇數，記為ch(G,σ)。顯然有ch(G,σ)≥χ(G,σ)。Jin、Kang與Steffen[9]等研究了符號平面圖的列表染色問題，證明了ch(G,σ)≤5對于任何符號平面圖(G,σ)成立。

設G是一個圖，如果可以通過刪除圖G的某些點與邊或者收縮圖G的某些邊得到圖H，則稱圖H是圖G的一個子式。著名的Wagner定理[10]指出：如果一個圖是平面圖當且僅當K5與K3,3都不是它的子式。因此，不含K5-子式的圖與不含K3,3-子式的圖均包含平面圖。

本文證明了ch(G,σ)≤5對于任何符號圖(G,σ)成立，其中圖G不含有K5-子式或K3,3-子式。因此，該結論推廣了上述提及的Jin、Kang與Steffen等人的相應結論。

2 幾類符號圖的列表點染色

2.1 相關定義與術語

設G是一個平面圖，C是圖G的一個圈。如果圈C關聯k個頂點，則稱其為k-圈。如果平面圖G中的一個圈C的內部和外部都包含圖G的頂點，則稱圈C是分離的。如果平面圖G的除了無界面的所有面的邊界都是3-圈，則稱G是一個近似三角剖分（注意此時無界面的邊界亦有可能是3-圈）。如果平面圖G的所有面的邊界都是3-圈，稱G是一個三角剖分。顯然，三角剖分一定是近似三角剖分。

設G1與G2為兩個圖，則圖G1∩G2的點集為V(G1)∩V(G2),邊集為E(G1)∩E(G2),圖G1∪G2的點集為V(G1)∪V(G2)，邊集為E(G1)∪E(G2)。

設G是一個不含K5-子式的圖，或不含K3,3-子式的圖，或平面圖。如果在圖G中任意添加一條邊所得到的圖含有K5-子式，或含有K3,3-子式，或是非平面圖，則稱圖G是邊極大的。

設φ是圖G的一個染色，圖H是圖G的一個子圖，則φ|H指的是圖H的一個染色，使得對于圖H的任何一個點v都有φ|H(v)=φ(v)，亦即φ|H是將染色φ限制在圖H上的一個染色。

2.2 延拓引理

本節將引入幾個重要的引理，用于下一節的主要定理的證明。

引理1[9]設(G,σ)是一個符號圖，其中G是一個近似三角剖分。記圈C=[v1,v2,…,vp]為G的無界面的邊界。如果L是(G,σ)上的一個顏色列表，其滿足L(v1)=α,L(v2)=β,α≠βσ(v1v2)，并且對于任何v∈V(C){v1,v2}有|L(v)|≥3，對于任何v∈V(G)V(C)有|L(v)|≥5，則符號圖(G,σ)具有L-點染色。

引理2設(G,σ)是一個符號圖，其中G是一個近似三角剖分。設L是(G,σ)上的一個顏色列表，其對于v∈V(G)有| |L(v)≥5。如果H是G的一個同構于K3的子圖，且λ是(H,σ)的L-點染色，則λ可以延拓為符號圖(G,σ)的L-點染色。

證明 記符號圖(H,σ)的3個頂點分別為u、v、w。由于H同構于K3，故它為圖G的一個3-圈。下面根據H是否為G的分離的3-圈分兩種情況討論。

情況1H不是G的分離3-圈。

由于G是一個近似三角剖分，故不妨假設H是G的最外面的3-圈，即H關聯著G的無界面。此時，在圖G中適當地添加邊（邊上的符號可任意給定）使得其成為一個三角剖分，仍記當前的符號圖為(G,σ)。

令G′=G-w。定義符號圖(G′,σ)上的列表L′如下：如果x是w在G中的異于u與v的鄰點，則令L′(x)=L(x){λ(w)σ(wx)}，否則令L′(x)=L(x)。記u,w1,w2,…,wt,v是w在G中所有鄰點，且按該順序依次排列在w的周圍。由于G是一個三角剖分，故G′是一個近似三角剖分，其無界面的邊界為圈C=[u,w1,w2,…,wt,v]。由于對于任何x∈V(C){u,v}有|L′(x)| ≥|L(x)|-1≥4，對于任何x∈V(G′)V(C)有|L′(x)|=|L(x)|≥5 ，故根據引理1可知：符號圖(G′,σ)具有L′-點染色φ，使得φ(u)=λ(u)且φ(v)=λ(v)。注意到φ(wi)≠λ(w)σ(wwi)對于所有的i∈{1,2,…,t}成立。故將φ與λ組合起來即得到符號圖(G,σ)的L-點染色，其中u、v、w的顏色分別為λ(u)、λ(v)、λ(w)。

情況2H是G的分離3-圈。

設(G1,σ)是所有點和邊都在H上或其內部的符號圖，(G2,σ)是所有點和邊都在H上或其外部的符號圖。顯然，G1與G2都是近似三角剖分且H不是G1的分離3-圈，也不是G2的分離3-圈。

將情況1的討論分別應用于符號圖(G1,σ)與(G2,σ)，可以得到 (G1,σ)的L-點染色φ1與 (G2,σ)的L-點染色φ2，使得φ1(u)=φ2(u)=λ(u)，φ1(v)=φ2(v)=λ(v)且φ1(w)=φ2(w)=λ(w)。因此，將φ1與φ2組合起來即得到符號圖(G,σ)的L-點染色，其中u、v、w的顏色分別為λ(u)、λ(v)、λ(w)。

引理3設(G,σ)是一個符號圖，其中G是Wagner圖（如圖1所示）。設L是(G,σ)上的一個顏色列表，其對于v∈V(G)有| |L(v)≥5。如果H是G的一個同構于K2的子圖，且λ是(H,σ)的L-點染色，則λ可以延拓為符號圖(G,σ)的L-點染色。

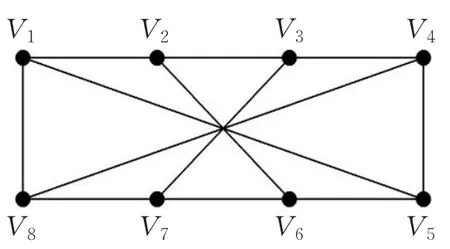
圖1 Wagner圖

證明 由Wagner圖的結構對稱性，下面僅需考慮兩種情況。

情況1H=v1v2。

此時，v1與v2上的顏色分別為λ(v1)與λ(v2)，且λ(v1)≠λ(v2)σ(v1v2)。接下來對圖中剩余的點按如下順序染色，即分別取：

λ(v3)∈L(v3){λ(v2)σ(v2v3)}

λ(v4)∈L(v4){λ(v3)σ(v3v4)}

λ(v5)∈L(v5){λ(v1)σ(v1v5),λ(v4)σ(v4v5)}

λ(v6)∈L(v6){λ(v2)σ(v2v6),λ(v5)σ(v5v6)}

λ(v7)∈L(v7){λ(v3)σ(v3v6),λ(v6)σ(v6v7)}

λ(v8)∈L(v8){λ(v1)σ(v1v8),λ(v4)σ(v4v8),λ(v7)σ(v7v8)}為點v3、v4、v5、v6、v7、v8上的顏色。從而λ已延拓為符號圖(G,σ)的L-點染色。

情況2H=v1v5。

此時，v1與v5上的顏色分別為λ(v1)與λ(v5)，且λ(v1)≠λ(v5)σ(v1v2)。接下來對圖中剩余的點按如下順序染色，即分別取：

λ(v2)∈L(v2){λ(v1)σ(v1v2)}

λ(v3)∈L(v3){λ(v2)σ(v2v3)}

λ(v4)∈L(v4){λ(v3)σ(v3v4),λ(v5)σ(v4v5)}

λ(v6)∈L(v6){λ(v2)σ(v2v6),λ(v5)σ(v5v6)}

λ(v7)∈L(v7){λ(v3)σ(v3v6),λ(v6)σ(v6v7)}

λ(v8)∈L(v8){λ(v1)σ(v1v8),λ(v4)σ(v4v8),λ(v7)σ(v7v8)}為點v2、v3、v4、v6、v7、v8上的顏色。從而λ已延拓為符號圖(G,σ)的L-點染色。

引理4設(G,σ)是一個符號圖，其中G是完全圖K5。設L是(G,σ)上的一個顏色列表，其對于v∈V(G)有| |L(v)≥5。如果H是G的一個同構于K2的子圖，且λ是(H,σ)的L-點染色，則λ可以延拓為符號圖 (G,σ)的L-點染色。

證明 記G的頂點分別為v1、v2、v3、v4與v5。由完全圖K5的結構對稱性，不妨設H=v1v2。

此時，v1與v2上的顏色分別為λ(v1)與λ(v2)，且λ(v1)≠λ(v2)σ(v1v2)。接下來對圖中剩余的點按如下順序染色，即分別取：

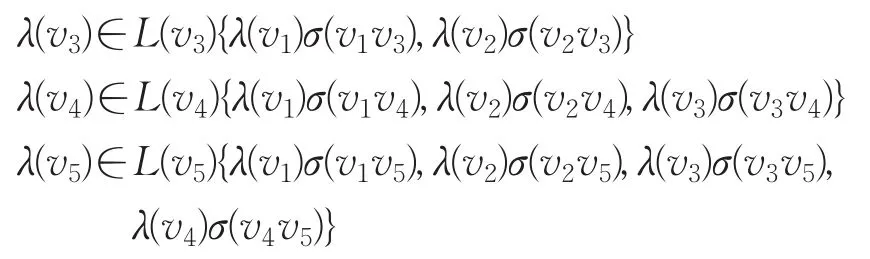
為點v3、v4、v5上的顏色。從而λ已延拓為符號圖(G,σ)的L-點染色。

2.3 列表點染色

本節將證明ch(G,σ)≤5對于任何不含K5-子式或K3,3-子式的符號圖(G,σ)成立。首先，下列兩個引理分別刻畫了不含K5-子式的圖與不含K3,3-子式的圖的結構。

引理5[11]如果圖G是邊極大的不含K5-子式的圖，則G=G1∪G2，其中G1是邊極大的不含K5-子式的圖，G2是邊極大的平面圖或者Wagner圖，并且G1∩G2=K2或K3。

引理6[11]如果圖G是邊極大的不含K3,3-子式的圖，則G=G1∪G2，其中G1是邊極大的不含K3,3-子式的圖，G2是邊極大的平面圖或者完全圖K5，并且G1∩G2=K2。

將上述兩個引理與第2.2節的延拓定理結合起來，可證明本文的兩個主要定理。

定理1如果(G,σ)是一個符號圖，其中G是不含K5-子式的圖。若L是(G,σ)上的一個顏色列表，其對于v∈V(G)有|L()v|≥5 ，則符號圖 (G,σ)具有L-點染色，即有ch(G,σ)≤5。

證明 在圖G中適當地添加邊使得其成為一個邊極大的不含K5-子式的圖。對于新添加的每條邊，其符號均設定為正。仍記目前得到的符號圖為(G,σ)。下面對圖G的頂點數進行數學歸納，證明定理1所述結論對于邊極大的不含K5-子式的符號圖(G,σ)成立，從而定理1得證。

由引理5可知，G=G1∪G2，其中G1是邊極大的不含K5-子式的圖，G2是邊極大的平面圖或者Wagner圖，并且H?G1∩G2=K2或K3。由歸納假設，符號圖(G1,σ)具有L-點染色φ1。在執行完染色φ1后，圖H的所有頂點均已經染好。

此時若H=K2，則當G2是邊極大的平面圖（即三角剖分）時，由引理1可知，φ1|H可延拓為符號圖(G2,σ)的L-點染色φ2；當G2是Wagner圖時，由引理3可知，φ1|H亦可延拓為符號圖(G2,σ)的L-點染色φ2。無論上述何種情況，將L-點染色φ1與φ2組合起來即得到符號圖(G,σ)的L-點染色。

另一方面，若H=K3，則G2不是Wagner圖（因Wagner圖中不含有三角形），從而G2是邊極大的平面圖，即三角剖分。由引理2可知，φ1|H可延拓為符號圖(G2,σ)的L-點染色φ2，然后將L-點染色φ1與φ2組合起來即得符號圖(G,σ)的L-點染色。

定理2如果(G,σ)是一個符號圖，其中G是不含K3,3-子式的圖。若L是(G,σ)上的一個顏色列表，其對于v∈V(G)有| |L(v)≥5，則符號圖(G,σ)具有L-點染色，即有ch(G,σ)≤5。

證明 在圖G中適當地添加邊使得其成為一個邊極大的不含K3,3-子式的圖。對于新添加的每條邊，其符號均設定為正。仍記目前得到的符號圖為(G,σ)。下面對圖G的頂點數進行數學歸納，證明定理2所述結論對于邊極大的不含K3,3-子式的符號圖(G,σ)成立，從而定理2得證。

由引理6可知，G=G1∪G2，其中G1是邊極大的不含K5-子式的圖，G2是邊極大的平面圖或者完全圖K5，并且H?G1∩G2=K2。由歸納假設，符號圖(G1,σ)具有L-點染色φ1。在執行完染色φ1后，圖H的所有頂點均已經染好。

此時當G2是邊極大的平面圖（即三角剖分）時，由引理1可知，φ1|H可延拓為符號圖(G2,σ)的L-點染色φ2；當G2是完全圖K5時，由引理4可知，φ1|H亦可延拓為符號圖(G2,σ)的L-點染色φ2。無論上述何種情況，將L-點染色φ1與φ2組合起來即得到符號圖(G,σ)的L-點染色。

3 結論

定理1與定理2指出任何不含K5-子式或K3,3-子式的符號圖的選擇數至多為5。由于一個圖是平面圖當且僅當K5與K3,3都不是它的子式（Wagner定理），故上述結論可以推出Jin、Kang與Steffen于2016年發表的如下結論：

推論1任何符號平面圖的選擇數至多為5。

由于無符號的平面圖可以看成是所有邊都是正邊的符號面圖，故可得如下結論：

推論2任何平面圖的選擇數至多為5。

由于Voigt[12-13]證明了存在選擇數恰好為5的平面圖，故推論2中的上界5是最優的。由此可推得：定理1與定理2中關于ch(G,σ)的上界5是最優的。

事實上，對于符號圖而言，除了研究其點染色與列表點染色之外，還可以研究其點蔭度與圓染色等相關的染色問題。感興趣的讀者可參考文獻[14-15]。