基于非相似原理快速查找多個shapelets

韋慶鋒，何國良

WEI Qingfeng,HE Guoliang

武漢大學 軟件工程國家重點實驗室，武漢 430072

State Key Lab of Software Engineering,Wuhan University,Wuhan 430072,China

1 引言

時間序列shapelets是時間序列中能夠最大限度地表示一個類別的子序列，是時間序列局部特征的表示，由Ye等人[1]所提出。shapelets算法采用時間序列局部片段進行分類，很大程度上避免了噪聲的影響，更加精確和健壯，同時，shapelets分類可以產生具有較高說明性的結果，能夠很明確地顯示出類別之間的差異之處，指明為什么一個特定的對象被分配到一個特定的類中，幫助研究人員更好地理解數據。shapelets已經作為時間序列領域一個重要的研究主題，受到了越來越多的關注[2-5]，還被應用到了醫療服務[6]、運動檢測[7]、電力需求分析[8]、聚類研究[9]等領域。

最早提出的基于shapelets分類是在查找出shapelets基礎上通過構建決策樹的方法來完成的，因此查找出shapelets的好壞決定了分類的效果。原始查找shapelets的方法要產生所有可能的候選集，然后依次計算它們的信息增益，找出最大的一個。它的時間復雜度為O(N2m4)，N為數據集中時間序列的個數，m為時間序列的長度，由此可見計算shapelets所需的時間是非常大的，這成為它被廣泛應用的最大障礙。尤其是隨著科技的進步，越來越多的領域都需要對以往產生的大量時間數據進行分析挖掘，有些數據不僅僅是單變量的，更多是多個變量相互作用、共同發展，如股票數據、氣象數據、多傳感器產生的運動數據等。已有的查找shapelets方法由于時間復雜度太高，已經不能適應當今數據挖掘的需求，迫切需要一種既能保持shapelets特性，又能縮短計算時間的方法。

本文提出了一種新的查找shapelets的方法（NSDS）：基于shapelets非相似的特性，根據子序列間距離分布設置一個距離閾值，從而過濾掉候選集中大部分相似子序列。再改變原始方法中計算耗時的信息增益為更加快捷的類可分離性計算，作為評價候選子序列的指標，最后得到得分靠前的多個子序列作為最終選擇出的shapelets。通過實驗表明，該方法在單變量時間序列數據集上查找出的shapelets的分類精度與已有方法相比有所提高，時間也得到了極大的縮減。NSDS方法擴展到多變量時間序列數據集后依然取得了不錯的效果。

2 相關研究

自從shapelets方法提出，針對shapelets分類的加速提取研究是大多數研究者所關注的領域，下面主要介紹國內外學者的相關研究。

文獻[1]中采用了提前停止距離計算和熵剪枝的加速方法，這兩種方法雖然簡單但是很高效，尤其是第一種方法，因為原始查找shapelets框架中共產生Nm2個候選子序列，每個候選子序列都需要計算與所有時間序列間的距離。若能減少距離的計算時間則可以大大提高整體算法的運行速度。

文獻[2]中使用了符號聚合近似（Symbolic Aggregate Approximation，SAX）對原始時間序列進行維度約減，將原始數據離散化表示為字符串。在此基礎上隨機遮蓋部分字符串統計剩下部分的相似性，結合類別號對區別能力進行打分，經過多次遮蓋后選取得分靠前的候選者，再進行后續的信息增益計算得到分類性能最好的子序列。

文獻[3]中利用了三角不等性[10]加速了子序列和時間序列間距離計算過程，主要是利用了以下數學原理：兩邊之差小于第三邊。具體來說先設置一個基準子序列O，然后計算兩個子序列A、B到O的距離之差作為距離下界dlb，A、B之間的實際距離一定是大于等于dlb的，當dlb大于已有的最小實際距離時，就可以放心地對A、B進行剪枝，這樣就減少了距離計算的次數。又采用了文獻[11]中證明的不同長度序列下界之間的關系，在只計算一次實際下界的情況下推導出更長子序列的下界，從而減少了下界的計算開銷。最后，再使用一個近似函數在遍歷子序列長度時不是每次往上加1長度，而是跳躍性地遞增。

文獻[4]提出了通過計算原始時間序列間的距離來對數據進行轉換，然后使用現有的分類方法（如SVM）查找shapelets；文獻[5]中使用了特征向量和融合正則化套索相結合的數學方法來尋找shapelets位置；此外，還有使用查找關鍵點[12]、非頻繁子序列[13]等技術剪枝shapelets候選集合的方法。

以上的大多數方法還是基于原始方法中查找shapelets框架的改進，在大量的候選子序列中去尋找能最好地表示一個類別特征的shapelet，雖然創新了許多距離計算方式、剪枝、距離下界等技術，但是運行效率不穩定，受數據集自身數據分布影響較大，在有些較大數據集上時間消耗還是難以接受。

3 基礎知識與符號

下面介紹一些本文中的基礎知識和符號：

定義1時間序列T和子時間序列s。

一個按時間順序排列的觀測值稱為一條時間序列T={t1,t2,…,tm}，每一個值ti表示該時刻下的記錄數值，m表示時間序列的長度。

時間序列T中一個連續片段稱為子時間序列i表示子序列的起始位置，l為子序列的長度。

定義2數據集D。

多個時間序列及其對應的類標號組成了一個數據集D=＜T1,c1＞,＜T2,c2＞,…,＜TN,cN＞，N表示數據集中的時間序列的數目。

定義3子序列距離。

兩條相同長度的子序列s、s′，經過Z標準化后使用歐氏距離計算它們之間的相似性，表示為：

定義4子序列和時間序列距離。

子序列和時間序列的長度不等，因此通過在長時間序列上依次滑動短序列找出最小距離作為兩者之間的距離，表示為：

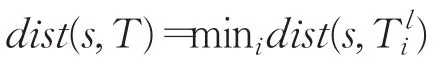
定義5相似性距離閾值。

通過對原始查找shapelets方法的研究發現：同類別時間序列中存在大量相似的子序列，不同類別中依然存在許多相似的子序列[14]，這是因為不同類別序列間的差異主要是來自那些局部具有特殊形態的序列片段，而非整體都是不同的。這些特殊片段往往范圍不是很大，卻有著能夠區分其他類別的特別形態，而余下的其他片段卻沒有關鍵信息，彼此之間差異很小。根據shapelets的特性（它對表征特定類樣本時距離很小，相反對其他類別時的距離較大），那些到任意類別距離都小的子序列是不可能成為shapelets的。基于以上分析使用子序列間距離表征相似性，設置一個距離閾值ε，當子序列之間的距離小于該閾值時，則認為它們之間是相似的，反之則是非相似的。通過這個閾值過濾掉候選集合中的相似子序列，省去后續無用的距離計算。ε的設置方法是對數據集中所有子序列間距離從小到大排序，統計其整體分布情況，確定某一累計總體距離比例p（事先設置參數）下對應的距離。

下面通過一個具體的實例來講解ε的設置方法：任意選擇3個單變量時間序列數據集（Fish，50words，InlineSkate），計算每個數據集中子序列間的距離，按從小到大的順序排列后統計在不同距離區間下的分布比例，所得到的數據使用Excel繪圖，結果如圖1所示，可見大多數分布都是傾向于距離較小一側的。以Inline-Skate為例，選擇數據集中累計占比p=0.25所對應的距離（該例中為1.7）設置為距離閾值，也就是說針對InlineSkate數據集子序列間距離小于1.7時認為它們是相似的。p值越小，過濾越多，候選子序列也就越少。通過第5章的實驗結果可以看到通過此方法可以過濾掉大部分的候選子序列，而只選擇少量的（約為0.1%）子序列進行距離計算。p值的設置需要視不同數據集的情況區別分析，沒有一個統一的數值，經過反復試驗本文中將其設置為{0.15，0.25，0.35}三者中的一個。

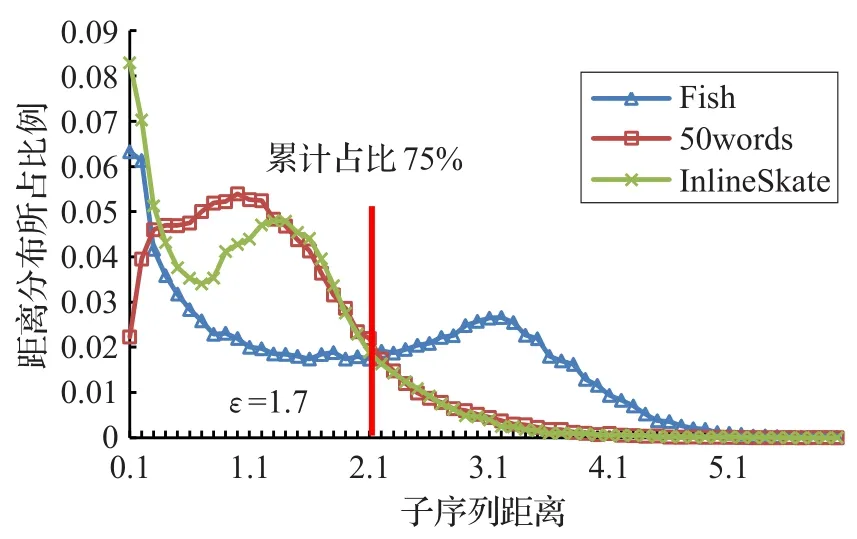
圖1 子序列距離分布

定義6基于離散矩陣的類可分離性。

假設有一組樣本(x,y)∈(Rd×Y)，其中Rd為d維特征空間，Y={1,2,…,c}為類標集合。樣本總數為N，ni表示第i類中的樣本個數，xi,j表示第i類中第j個樣本，u為所有類別的樣本均值，ui為第i類對應所有樣本的均值。則類間離散度矩陣Sb和類內離散度矩陣Sw定義為：

基于離散矩陣的類可分離性為兩者的跡或者行列式的比值，即J=Sb/Sw，J值越大，表示類可分離性越好[15]。

對于一個候選子序列candidate，計算它與所有時間序列的距離，直觀表示如圖2所示，其中紅色矩形代表的是candidate和類別1樣本的距離，綠色三角形代表的是和類別2樣本的距離。按距離大小映射到一維坐標后，按照類內類間離散度矩陣的定義進行計算，就可以通過類可分離性來評價該候選子序列分類性能，得分越高表明該子序列分類性能越好。

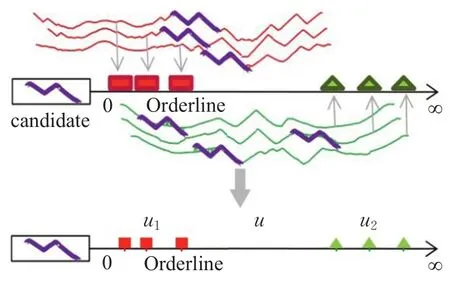
圖2 基于離散矩陣的類可分離性

4 非相似shapelets快速查找

4.1 算法綜述

在第3章理論與技術基礎之上，給出了步驟嚴密的算法。整體思路是首先通過距離閾值過濾掉相似的子序列，再使用類可分離性對過濾后的子序列進行評價，從中選擇得分靠前的部分為shapelets，最后使用選擇出的多個shapelets對測試序列進行分類。

4.1.1 計算距離閾值

算法1computerThreshold

輸入：訓練集Tr（樣本數N，長度m，類標集合C={1,2,…,c}），累計比例p，shapelets長度集合Φ∈RL。

輸出：距離閾值ε。

1.Y←?;

2.for 1,2,…,Nm

3.i←rand(N);Φl=rand(ΦL);j=rand(m-Φl+1);

4.i′←rand(N);j′=rand(m-Φl+1);//隨機選擇子序列起始位置和長度

5. select random candidate:s←Ti,j:j+Φl-1;

6. select random candidate:s′←Ti′,j′:j′+Φl-1;

7.Y.add(dist(s,s′));//計算子序列間距離加入到Y集合

8.sort(Y);

9.ε=Y[p];

距離閾值ε的計算是該算法的基礎，它決定著過濾性能的好壞，按照定義5中介紹的原理與方法，具體計算過程如算法1所示。先初始化一個集合Y用來存放子序列間的距離，設置一共需要計算的子序列組數為Nm，任意選取兩條長度相同位置不同的子序列（步驟2～6），按照定義3計算子序列之間的距離，將得到的距離存放于Y中（步驟7）。此處在選擇子序列對時，不是將全部可能位置可能長度的子序列全部計算一遍，而是使用了固定數量下隨機選取的方法，這樣做的好處是保證了與總體分布誤差很小的情況下大大減少了比較的次數，降低了整體計算的時間復雜度。等到所有的子序列間距離計算完后對Y進行排序（步驟8），得到事先設置好的參數——累計比例p下對應的距離（步驟9）。

4.1.2 查找shapelets

算法2DiscoveryShapelets

輸入：數據集Tr（樣本數N，長度m，類標集合C={1,2,…,c}），累計比例p，PAA壓縮比例r，shapelets長度集合Φ∈RL，shapelets個數k。

輸出：kShapelets,kDistance。

1.R=?;B=?;disToShapelets=?;

2.ε←computerThreshold(Tr,p,Φ);//計算距離閾值

3.for 1,2,…,NmL

4.i←rand(N);Φl=rand(Φl);j=rand(m-Φl+1);

5. select random candidate:s←Ti,j:j+Φl-1;

6. if!similarWith(s,B)//候選子序列和已選子序列是否相似

7.Dis←dist(s,Tr);

8.score(s)=ClassSeparability(Dis,C);//計算類可分離性

9.disToShapelets.add(Dis);B.add(s);

10. elseR.add(s);

11.sort(score);

12.kShapelets←selectK(B);

13.kDistance=selectK(disToShapelets);

查找shapelets過程如算法2所示：給定一個時間序列訓練集Tr，先對其中的時間序列進行Z標準化，使得處理后的數據滿足標準正態分布。然后有選擇地根據數據集大小進行PAA（Piecewise Aggregate Approximation）處理來降低時間維度。對原始數據預處理結束后，初始化備用集B、拒絕集R和子序列到時間序列距離集disToShapelets為空（步驟1），集合B中存放的是非相似子序列，R中存放的是與B中相似的子序列。然后計算距離閾值ε（算法2）。在選取候選子序列s時，并沒有按照原始方法中的滑動窗口遍歷每一種子序列，然后再增加窗口寬度重復滑動的方法，而是采取了隨機選擇起始位置，隨機選擇子序列長度的方法。為了不失一般性，將最外層的循環次數設置為NmL（步驟3），產生的隨機數滿足均勻分布，這樣做和原始方法中候選集的數目差不多。隨機選取一條候選子序列（步驟4、5），計算它與備用集B中子序列間的距離（步驟6），若大于閾值ε，就將它加入到B中，否則加入到拒絕集R中。對加入到備用集B中的子序列，計算它與訓練集中所有時間序列的距離dist(s,Tr)，再通過類可分離性（定義6）對dist(s,Tr)計算評價得分score，并將dist(s,Tr)加入到距離集合disToShapelets中（步驟7～10）。待全部候選子序列計算完成后將B內子序列按照得分非遞增的順序排序（步驟11），最后選擇得分靠前的k個子序列作為kShapelets及其對應的kDistance（步驟12、13）。

4.1.3 對測試序列分類

算法3oneNN(Te,kShapelets,kDistance)

輸入：測試集Te（樣本數N，長度m，類標集合C={1,2,…,c}），選擇出的k個shapelets及其對應的訓練集的距離kDistance。

輸出：分類準確率Accuracy。

1.correctNum=0;

2.fori=1:N;j=1:k

3.testToShapelets=dist(kShapeletsj,Tei);

4.testToTrain=testToShapelets-kDistance;//經處理轉換后測試樣本和訓練樣本間距離

5.classVal=argmin(testToTrain);//將最近鄰測試樣本的類標號作為分類結果

6. ifclassVal==testClassi

7.correctNum++;

8.Accuracy=correctNum/N;

查找出shapelets的根本目的是為了對測試序列進行分類，原始方法中使用的是決策樹的分類方法。這樣做的不足之處是：

（1）決策樹中每個節點是唯一shapelet，若此shapelet性能不好，將導致分類的徹底失敗；

（2）對于多分類問題就要選擇多個shapelets，而原始方法中就只能通過多次查找來解決，這樣做非常耗時，而且有選擇相似shapelets的風險。

為了解決這些問題，將由算法2得到的kDistance看成是k個特征屬性組成的向量，每個特征為一個shapelet到所有訓練序列的距離。對測試序列和k個shapelets進行距離計算后，也將得到包含k個屬性的特征向量。再使用1-NN分類方法尋找每個測試序列的最近鄰訓練樣本，以此來確定測試序列的類別，具體過程如算法3所示。對于訓練集Te中每個樣本，計算它與kShapelets的距離，得到一個長度為k的距離向量testToShapelets（步驟3），然后與訓練集kDistance中尋找距離最近的樣本對應的類標號作為該測試樣本的類別（步驟4、5），若與真實類別相同則correctNum累加1（步驟6、7）。最后返回整體的準確率。

4.2 參數分析

4.2.1 PAA的壓縮比例設置

算法2中提到算法開始前有選擇地對原始數據進行PAA降維處理，若使用PAA的壓縮比例r={1/2,1/4,…}，r值越小則降維幅度越大；但是降維后的數據會忽略掉一些原始特征，有可能影響后續的分類效果，因此r值也不能設置得過小。在圖3中根據此問題測試了3個數據集，分析它們在使用不同的PAA壓縮比例r后的分類效果。隨著r的減小，分類準確率會有所降低，時間消耗降低較為明顯。因此只要r值設置得合理，可以減少計算時間，分類精度也沒有太大的影響。

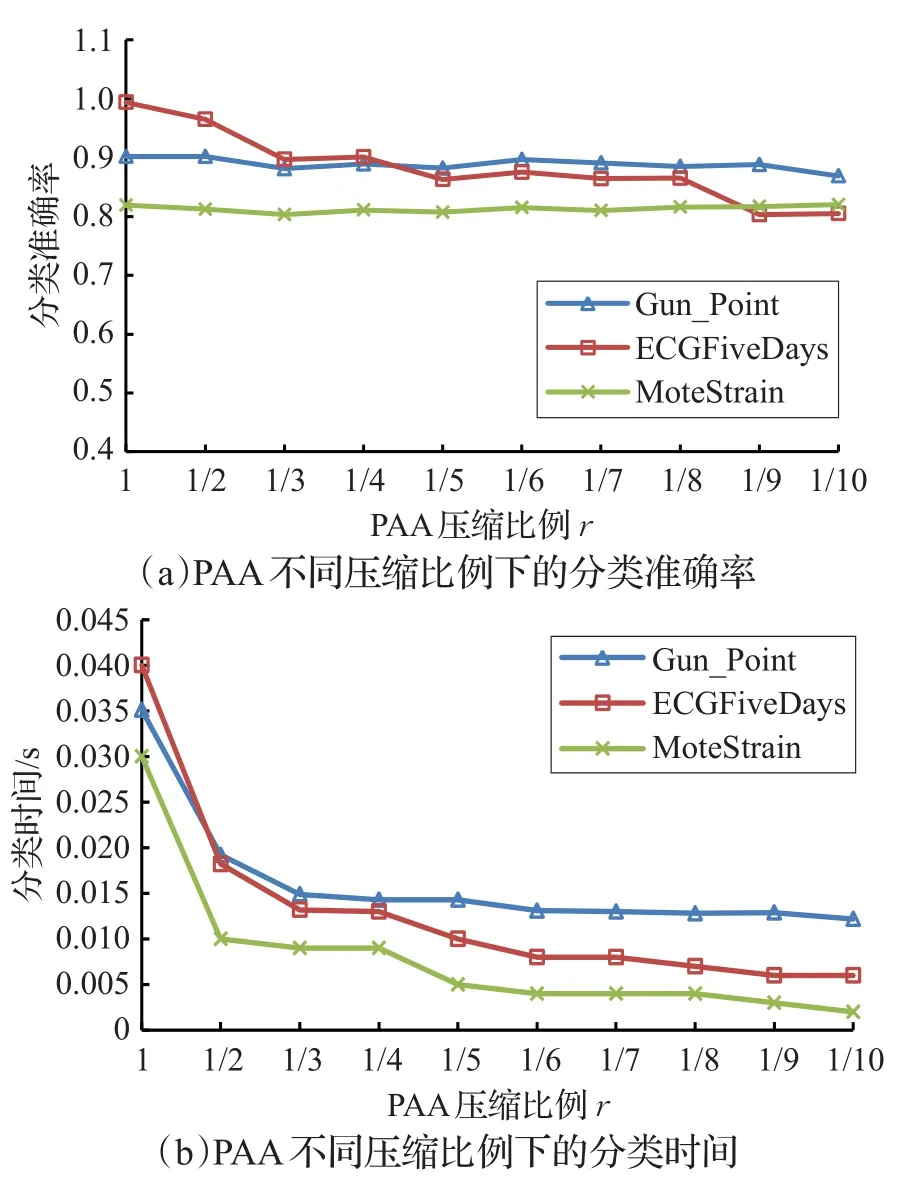
圖3 PAA不同壓縮比例下的分類對比

4.2.2 子序列長度的設置

在搜索不同長度的候選子序列時，原始方法中采用的是窗口逐步加1的方式，這樣做雖然可以把每種可能性都考慮到，但是低效。因為shapelet的核心思想是找出那些代表特征的時間片段，只要是包含了這些關鍵特征，無論是長序列還是短序列對分類是沒有太大差別的，所以原始方法中一個很突出的問題就是最終選擇出的shapelets之間有很大的重合，而這些重復計算占用了大量的時間，最終導致效率低下。為了解決這一問題，在設計shapelet長度集合Φ時把候選長度設置為若干個固定值。為了證明此方法的有效性，假設選取子序列的長度為0.2～0.6 m，將此長度區間平分為n(n=3,4,…,15)份，也就是子序列長度有n種可能，統計查找出的shapelets分類情況，結果如圖4所示。由結果可得，子序列長度可選范圍的大小對分類精度影響不大，但是長度數量越多，花費的時間也就越多。在本文的實驗中，統一設置子序列長度為Φ={0.2 m,0.4 m,0.6 m}。

圖4 不同子序列長度下的分類比較

4.2.3 shapelets數量的設置

算法2步驟12和13中選擇得分靠前的前k個子序列，k值大小對后續分類準確率和時間影響較大，這是一個對算法性能有重要影響的參數。因此做了以下實驗：令k值由小變大，分析它對分類精度的影響，結果如圖5所示。因為shapelets數目只會影響到測試集分類時間和結果，對訓練集尋找shapelets的時間沒有影響，所以只給出了分類準確率的結果。雖然沒有分類時間的比較，但是顯然知道：分類時間和shapelets數目成正比關系。由結果可得：選取較少的shapelets時，會降低分類準確率，隨著數目的增加，準確率有所上升，到一臨界值時數目再增加，準確率也不會發生變化。不同的數據集臨界值不同，在后面的實驗中將k統一設置為備用集B中子序列總量的50%。

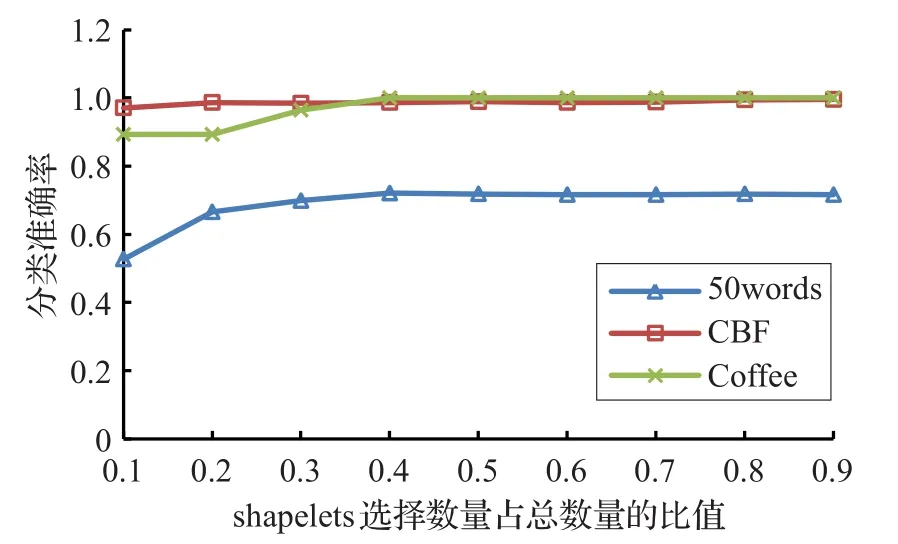
圖5 選擇不同shapelets數目對分類的影響

4.3 時間復雜度分析

對于樣本數為N、時間長度為m的數據集，原始算法中shapelet候選集的大小為Nm2，查找最好的shapelet時間復雜度為O(N2m4)。若使用PAA進行時間維度的降維，其壓縮比例r={1/2,1/4,…}，那么降維后的時間復雜度為O(r4N2m4)。通過設置一個距離閾值可以對候選子序列進行過濾，假設過濾的比例為其中為備用集合中子序列的數量，為拒絕集中子序列的數量。因此，若PAA和過濾子序列的方法同時被使用，候選集的大小為fNr2m2，最終查找多個shapelets的時間復雜度為O(fNr2m2×Nr2m2)=O(fN2r4m4)。本算法還需要額外計算兩部分：計算距離閾值和比較候選子序列與已選子序列間的相似性，前者的計算復雜度為O(Nrm×rm)=O(Nr2m2)；后者的復雜度為O((1-，其中為子序列長度可能取值的數目，根據4.2節中的分析，由于的數量級為1～2，因此額外需要計算部分的復雜度為O(2Nr2m2)，相比于過濾后的子序列中查找shapelets的時間復雜度O(fN2r4m4)相差1～2個數量級，所以最終的時間消耗為O(fN2r4m4)。本方法和原始方法計算時間比值是fr4，第5章的實驗結果同樣驗證了此分析的結論，由此可見NSDS方法可以大大縮短計算時間。

5 實驗結果

5.1UCR數據集

為了評價本文新提出的非相似shapelets快速查找方法（NSDS）的有效性，選用了UCR作為單變量時間序列數據集[16]，它們中大多數已被用到時間序列的仿真實驗中，每個數據集的具體信息描述如表1所示，采用原數據集中默認的訓練集和測試集。分類器采用1-NN，使用歐氏距離計算樣本之間的相似性。實驗環境為Core i7四核CPU，主頻3.60 GHz，內存8 GB，Windows 8系統，使用Java編程語言。對比算法選用文獻[2]中提出的FS算法。

5.2 單變量時間序列分類性能

將NSDS方法和FS方法在每個數據集上分別計算10次，取其平均值作為最終的實驗結果，如表2。其中第3～5列的r、p、k分別對應算法2中的3個輸入參數：PAA壓縮比例、距離累積比例、最終選擇shapelets集中的數目。通過設置不同的參數，經過多次實驗，取最好分類結果時對應的參數值。第6列的數值表示的是最終選擇出的shapelets子序列數目占所有候選子序列的比值，當該比值小于0.001時只進行標記，未給出精確數值。最后4列代表著兩種方法各自的分類準確率和查找shapelets時間，為了明顯起見，將分類準確率高和運行速度快的數值加粗表示。

由表2結果可得：NSDS方法在分類準確性上要優于FS方法，在所有的45個數據集中有33個數據集使用NSDS方法分類準確性更高，最大地提升為Cricket_Z數據集的0.285，最小的為ECGFive數據集上的0.003，平均為0.101。相對地在另外12個數據集中，FS方法分類準確性優于NSDS方法的幅度都較小，最大的也只有0.046，最小的為0.003，平均為0.022。

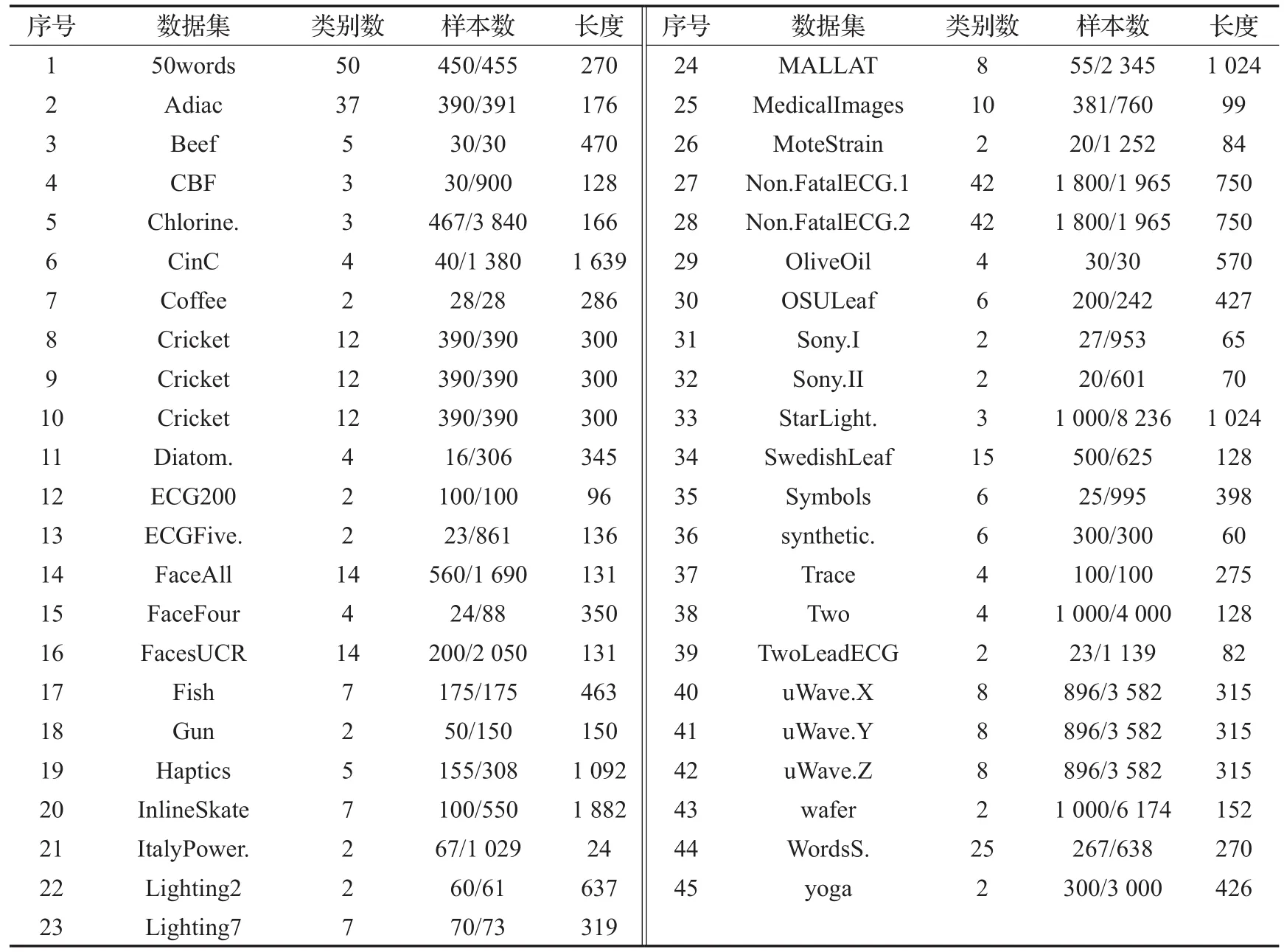
表1 UCR時間序列數據集

表2 UCR數據集分類準確率和時間對比

圖6為兩種方法分類準確率比較的直觀顯示，圖中左上部分的區域代表FS算法查找出的shapelets分類準確率較好，相反的右下部分代表NSDS方法較好，且距離對角線越遠的區域代表兩者之間差別越大。從圖6中可以明顯看到大約3/4數據集的結果都落在了NSDS區域，且整體偏離對角線的幅度大于落在FS區域里的數據集，這和之前的定量分析相一致。

圖6 NSDS方法與FS方法分類準確率比較

在查找shapelets時間方面，NSDS方法一致優于FS方法，并且優勢非常明顯，平均都要快3～4個數量級，與4.3節中時間復雜度分析的fr4相一致。最大的速度提高是InlineSkate數據集，提高了119354倍。在每個數據集上的查找時間都控制在幾秒以內，這無疑對后續的數據挖掘或者是計算能力不是很強的設備提供了可能性。NSDS的計算時間之所以能夠如此之短，除了PAA降維的作用之外，更主要是因為使用了距離閾值過濾候選子序列的方法，從表2中可以看出最終選擇出的shapelets子序列數目占所有候選子序列的比值都非常小，大多數都在10-3級別，最大的也僅有0.07。剩下的少數子序列計算它們與時間序列的距離也就變得非常容易，這種先過濾后計算方式可以最大程度地減少時間復雜度，優于先計算后過濾的方式[17]。

5.3 shapelets可解釋性

知道使用shapelet進行分類的一個很大優勢是它具有良好的可解釋性，能夠很明確地顯示出類別之間的差異之處，指明為什么一個特定的對象被分配到一個特定的類中，幫助研究人員更好地理解數據。在本文方法中是選擇出最好的k個shapelets，通過類可分離性評價好壞，那么這k個shapelets是否依然保持了良好的可解釋性呢，為此將所選擇出的shapelets結果繪制出來，結果如圖7所示。

由圖7可得，圖（a）中為Trace數據集中不同類別的樣本直觀表示，可見每種類別都有自己獨一無二的特性，如類別1中在時間點50附近有一個短暫的高峰，類別2和類別1的區別就是沒有這種高峰，顯然這個短暫的高峰就是一個shapelet。圖（b）中為通過NSDS算法得到的shapelets中部分子序列，很明顯shapelet1包含了之前人為分析應該為shapelet的片段，同樣另外2個也包含了其他類別顯著的特征。該結果同時也說明了shapelet只需要包含這些關鍵特征，長序列和短序列是沒有太大差別的。

5.4 多變量時間序列數據分類性能

圖7 Trace數據集中NSDS方法選擇出的shapelets

目前使用較多的多變量時間序列分類方法是基于實例的，也就是說選擇合適的相似性度量方法計算實例之間的距離，再按距離大小進行分類。例如，基于動態時間彎曲（DTW）和K-NN的多變量時間序列分類方法使用非常廣泛，但是在某些數據集上表現得并不是很理想[18]；或者是使用特征表示方法，對原始數據進行特征提取，再進行分類[19]；還有的學者將多種處理手段融合，比如Banko和Abonyi[20]將基于PCA的特征提取方法與DTW相似性度量方法相結合，轉換后的數據保留了變量間的相互關系；Prieto等人[21]提出了分層分類的策略，先使用多分類器對每個變量進行學習，融合底層分類結果后再使用高層學習器確定最終類別。

以上這些方法有的計算復雜度很高，有的在處理過程中丟失了原始數據的物理特性，有的經過復雜計算后對分類性能提升并不高。結合本章對子序列shapelet的學習，使用基于多個shapelets的組合分類器方法來對多變量時間序列分類。具體來說就是對每個變量使用NSDS方法尋找多個shapelets，然后使用1-NN方法分類，這樣就構建出d個分類器（d為變量數），采用投票的方式融合多分類器的結果作為最終分類類別。

人體活動識別是指在測試者身上放置多個運動感應器來記錄活動數據，并對這些數據進行挖掘來獲得運動模式的過程，該研究鄰域近幾年隨著運動記錄設備的普及化而得到了越來越多的關注[22-24]。這些活動數據從本質上來說就是多變量時間序列，每個變量代表著一個感應器獲得的時序數據。因此實驗中選用文獻[22]中介紹的Daily and Sports Activities Data Set作為實驗數據。

表3 NSDS方法在運動數據集上分類結果

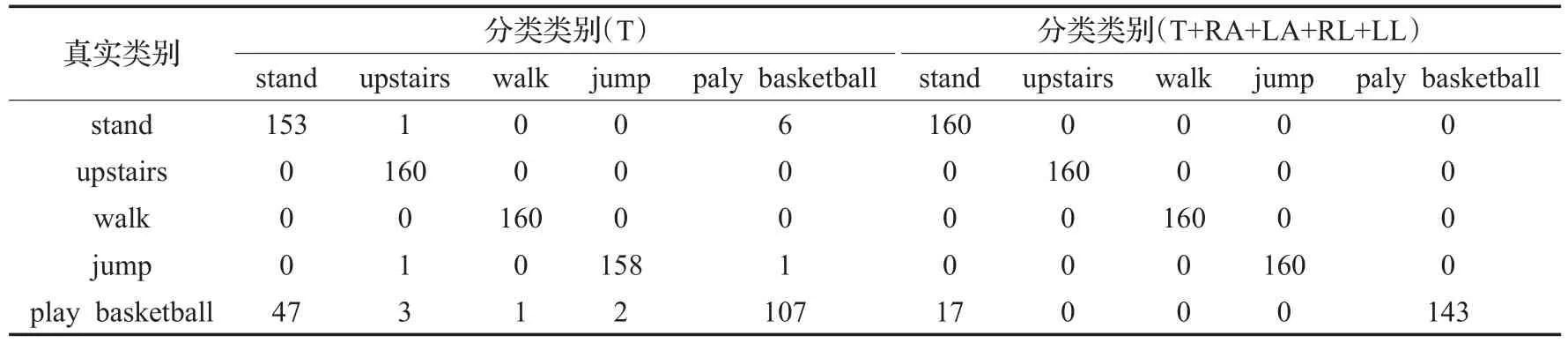
表4 不同感應設備下的混淆矩陣

Daily and Sports Activities Data Set是由Bilkent University從8個實驗者采集而得：在每個實驗者身上的5個不同部位放置5個感應設備采集19種動作的運動時間序列。每個設備包含多個加速度計、陀螺儀、磁強計感應器，最終得到數據集包含9120個樣本，每個樣本變量維數45，時間維數125。本實驗選擇其中5類常用的動作（站立、行走、上樓、跳躍、打籃球），也就是共2400個樣本。隨機選擇其中2/3作為訓練集，1/3作為測試集，PAA壓縮比例r設置為0.5，距離累積比例p設置為15，重復10次，取平均值作為最終結果，如表3所示。

由表3結果分析可得：根據測試者身上感應設備的多少而采集到的數據集變量數是不相同的，分別使用單一感應設備和組合感應設備來對運動進行識別。表中第2列代表不同的放置部位：T（軀干）、RA（右胳膊）、LA（左胳膊）、RL（右腿）、LL（左腿）。顯然NSFS方法對運動識別的準確率較高，當僅使用一個感應設備時，可以達到最低91.275%、最高95.125%的準確率。其中放置在右腿的感應設備采集的數據分類準確率最高，這和人們的常識也相一致：腿部動作幅度最大。隨著變量數的增加，分類準確率逐漸增加，查找shapelets和分類所需的時間也在逐步增加，當使用全部5個感應設備時，分類準確率達到97.625%，這說明了有些動作是需要身體各部位協作來完成的，如果只是觀察其中某個部位錯誤分類的可能性也就越大。

為了更加深入地分析該數據集，給出了表3中序號1和序號9實驗中一次結果的混淆矩陣，如表4所示。表中各行代表真實類別，各列代表使用NSDS方法得到的預測類別。對于upstairs和walk兩個動作，使用基于軀干的傳感器和所有傳感器都可以做到完美分類，錯誤率為0；stand和jump動作中有個別樣本被錯誤分類；分類效果最差的是play basketball動作，在兩種情況下的分類錯誤數分別為53和17，相應的錯誤率為33.125%和10.625%。其中主要是被錯誤分類成stand動作，在使用基于軀干的傳感器時有47次被錯誤分類成stand動作，使用全部傳感器時這一錯誤次數為17。分析其中的原因是和數據自身采集時有關，因為數據在采集時要求測試者連續完成每個動作5 min，然后將所收集的數據按照5 s的窗口劃分成60等份，在做play basketball這個動作時，中間會有短暫的靜止狀態，這些靜止狀態被劃分成小塊時就會和stand動作很相似；其次因為play basketball這個動作更多的是手臂的參與，而軀干有時會處于靜止狀態，所以在只使用T時play basketball被錯誤分成stand的次數遠遠高于使用全部感應設備。

6 結束語

本文提出了一種快速查找非相似時間序列shapelets的方法，充分利用shapelets思想的特性，而不拘泥于原始方法中的框架，使用了多種加速方法和近似計算，在不影響分類精度甚至是提升精度的情況下極大地減少計算時間。為解決多變量時間序列的shapelets問題或者計算能力不強的設備上使用shapelets問題提供了一種可行的選擇。在后續的工作中將會繼續致力于時間序列shapelets的研究問題，進一步改進本方法，減少參數的輸入，盡量減少人為因素的影響，增強算法的魯棒性。