引入勢場及陷阱搜索的強化學習路徑規劃算法

董培方，張志安，梅新虎，朱 朔

DONG Peifang1,ZHANG Zhi’an1,MEI Xinhu2,ZHU Shuo1

1.南京理工大學 機械工程學院，南京 210094

2.南京理工大學 計算機科學與技術學院，南京 210094

1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China

2.School of Computer Science and Technology,Nanjing University of Science and Technology,Nanjing 210094,China

1 引言

隨著無人駕駛的興起，移動機器人路徑規劃技術越來越受到人們的重視。作為移動機器人自主移動的核心技術，有大量的科研人員投入到相關的研究工作中。傳統的路徑規劃技術有人工勢場法、圖解法、動態窗口法[1]等，基于人工智能的路徑規劃技術有遺傳算法[2]、神經網絡[3]、蟻群算法[4]等，每種方法都存在一定的局限性。傳統方法在復雜的環境地圖中易陷入陷阱中無法逃逸，有較大的概率無法到達目標位置；而智能算法計算量龐大，需要進行較多的迭代次數之后才能規劃成功。強化學習算法是根據獎勵和懲罰機制來提高對特定任務的完成能力，其探索和貪心思想適用于未知環境中的路徑規劃，隨機探索的概率越大則最終獲得的路徑越優，理論上能滿足任意復雜環境的路徑規劃，具有較強的可開發性。

Q學習（Q-learning）算法是強化學習中的一種高效離策學習算法，傳統的Q-learning算法基于馬爾可夫過程，采用隨機初始化，對環境的先驗信息為0，初始路徑較為隨機，導致路徑規劃效率低下，訓練所需的迭代次數過多。基于此，研究人員提出了多種方法初始化Q值函數加快路徑規劃的迭代速度，有神經網絡法、模糊規則法[5]、人工勢場法[6-8]等。人工勢場法規則簡單，效率較高，但在復雜環境中基于障礙物的斥力勢場數量多，計算量大。針對Q-learning算法的迭代速度慢，本文提出了引力勢場和環境陷阱搜索聯合作為先驗信息初始化Q值，避免了復雜環境中斥力勢場龐大的計算量，同時有效防止了移動體陷入環境中的凹形陷阱，加快了算法的迭代速度。同時取消對障礙物的試錯學習，縮小可行路徑的范圍，使訓練能應用于真實環境中。最后，通過python及pygame模塊在復雜環境中進行仿真實驗，驗證了算法的可行性和高效性。

2 強化學習機制

強化學習方法是指智能體（agent）通過在環境中按照一定的策略探索，根據環境的獎勵和懲罰機制不斷調整行為策略，以獲得最大的回報值作為最終行為目的。在標準的強化學習框架中，包括智能體（agent）、環境及4個基本要素[9]。

（1）策略（policy）

策略π是智能體與環境交互時的行為選擇依據，S→A是狀態空間到動作空間的映射，智能體在狀態St下根據π選擇動作at+1∈A。

（2）獎懲函數（reward）

獎懲函數r反映當前環境狀態St∈S（S為狀態空間集）下的動作at∈A（A為動作空間集）對達成目標的貢獻度，r值越大代表當前環境下的動作越有利于達成目標。

（3）值函數（value function）

值函數V是agent在環境下行動的期望回報，強化學習通過不斷地試錯來迭代值函數，以獲得較大期望回報，用于提高高回報值的狀態動作選擇概率而降低低回報值的環境狀態選擇概率。

通過對值函數評估來不斷改變對應狀態的行動策略，以達到最大化回報：

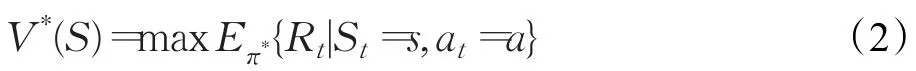
（4）環境模型（model of environment）

環境模型強化學習的基本運行環境，包括環境狀態及其對應的動作映射空間。

3 Q-learning算法模型

Q-learning算法是基于時序差分（Temporal-Difference，TD）誤差的離策強化學習算法，采用了動態規劃的思想，根據下一步的最大動作-狀態值函數作為動作選擇的策略：

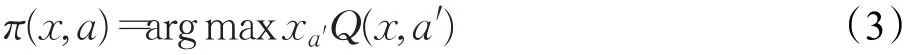
基于Q-learning的強化學習方法建立在馬爾可夫決策過程理論框架上，即智能體與環境的交互過程中，t時刻的狀態St只與上一個狀態S(t-1)下所采取的動作a(t-1)有關，而與歷史狀態和動作無關，即：

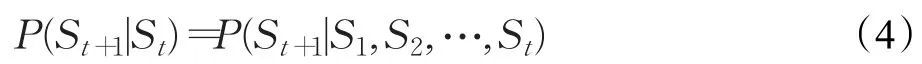
Q-learning更新函數：

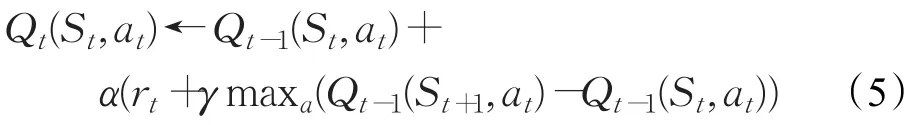
其中，α為學習率，學習率越大，迭代速度越快，但易過擬合；γ為折扣率，即未來獎勵對當前動作的影響程度[10]。

4 加入環境初始信息的快速Q-learning迭代算法

傳統的Q-learning算法無環境先驗信息，初始狀態的所有狀態值函數V(s)均相等或完全隨機，每一步動作a產生于隨機狀態，即此時的MDP環境狀態轉移概率是均等的。對于路徑規劃問題而言，只有在達到目的地或者碰到障礙物才會更改回報值R，進行一次有效的狀態-動作值更新，回報函數的稀疏性致使初期的規劃效率低，迭代次數多，特別對于尺度較大的未知環境，易出現巨大的無效迭代搜索空間[11-12]。

結合人工勢場法和陷阱搜索的基本思想改進基于Q-learning算法的路徑規劃：

（1）確定起始點坐標a和目標點坐標b，在初始化狀態值函數中以目標點為勢場中心建立引力勢場，根據目標點的位置作為環境先驗信息初始化V(S)表，設定初始化后的V(S)值均大于等于0。

（2）對環境地圖進行4個方位的逐層搜索，若發現障礙物，則進行V(S(t+1))=-A操作，若發現陷阱區域，則對該區域進行逐層向外搜索，每層之間設置梯度值-B,并通過Lmax＜A/B，保證陷阱區的最外層狀態值為負數。

（3）利用環境狀態值函數更新狀態-動作值函數表：

（4）智能體從起始點開始探索環境，只把V(S(t+1))≥0的狀態作為可探索狀態，采取可變貪心法則，每移動一步更新一次狀態-動作值。到達目標點后結束此輪迭代，從起始點開始進入下一輪探索。

4.1 改進人工勢場法

人工勢場法的基本原理是在目標物周圍產生虛擬引力勢場，智能體在任何位置都受到來自目標點的引力吸引，而障礙物對移動物體產生排斥力，阻止物體靠近產生碰撞[13]。

引力勢場函數：

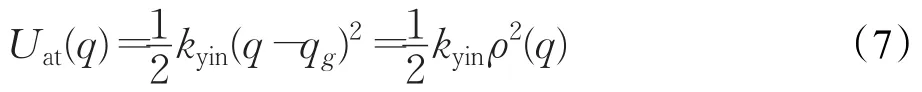
式中，kyin為引力常數；ρ(q)=||q-qg||是智能體與目標位置的歐幾里德距離。

基于改進引力勢場法初始化狀態值函數法則：Q-learning算法是基于馬爾科夫決策的無模型強化學習算法，采用可變ξ-greedy法則[14]，其行為策略是往Q值增大的方向移動，因此對于初始化狀態值函數表，應滿足距離目標點越近其引力勢場越大，與距離成反比（傳統的引力勢場與距離平方成正比），為了保證算法的實時性，不考慮障礙物的斥力勢場，同時減小公式計算復雜度，引入參量L用于調整初始狀態值的變化范圍：

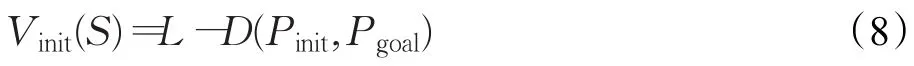
D(Pinit,Pgoal)=為起始點和目標點之間的距離。

對于復雜環境的Q-learning算法路徑規劃，動作狀態空間龐大，迭代速度慢，引入目標點改進引力勢場來初始化狀態值函數，從而提供初始目標位置，智能體具有目標趨向性，能迅速朝目標方向移動，同時隨機策略保證其不陷入局部最優解。

4.2 環境陷阱搜索算法

在復雜環境中，常常存在凹形障礙物，對于人工勢場法或蟻群算法等易陷入凹形區域，無法到達目標點。基于強化學習算法的路徑規劃能夠通過隨機探索策略和策略改進逃離此類障礙物，這種智能行為是高效導航基礎[15]，但規劃效率低，只引入引力勢場的強化學習算法由于目標趨向性同樣容易陷入與目標相對的凹形障礙物中，需要較多的訓練次數才能逃逸，如果能直接將凹形障礙物從可行的規劃路徑中剔除，則能提高規劃的效率，減少迭代的次數。

針對此類障礙物，提出沿x、y方向的陷阱逐層搜索，并把搜索結果作為環境先驗信息初始化狀態函數表V(S)。

陷阱搜索算法如下：

步驟1將探索環境柵格化，并對障礙物進行膨脹處理，將移動物體（agent）看作質點。以地圖某一頂點作為坐標原點建立直角坐標系（如圖1所示，黑色為障礙區，白色為可行區域）。建立當前層疑似陷阱長度存儲數組Suspect-trap[]、層數存儲數組Trap-length[]以及當前層陷阱個數存儲數組Trap-number[]。初始點坐標為a(x,y)，目標位置的坐標為b(x,y)。對柵格地圖進行4個方向的逐層搜索，如圖1為沿X正方向進行層內搜索，Y正方向進行層級搜索，即沿柵格內數字順序搜索。

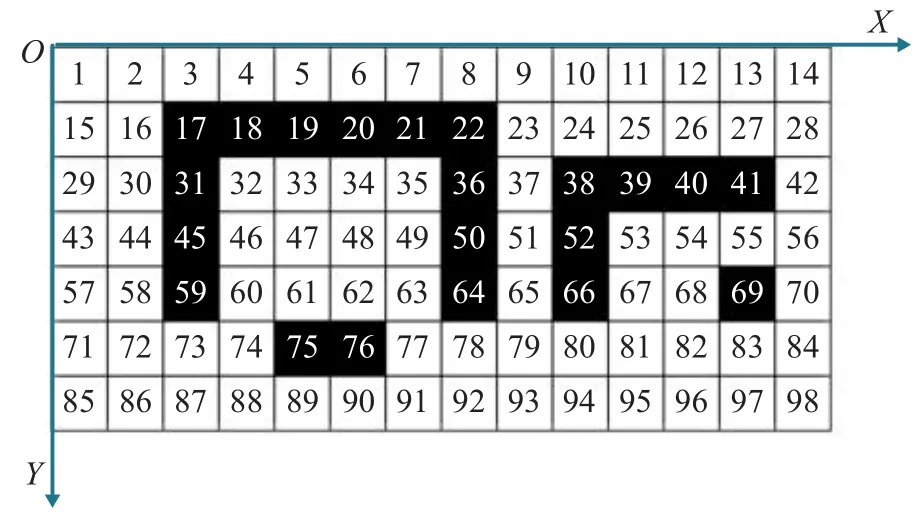
圖1 柵格地圖

步驟2利用改進人工勢場法初始化狀態函數表，距離目標點越近，狀態值越大，非障礙物區域狀態值大于等于0，障礙物區域狀態值為-A(A＞0)，陷阱層數為N，陷阱狀態梯度值為G，已標記陷阱區域狀態值為：

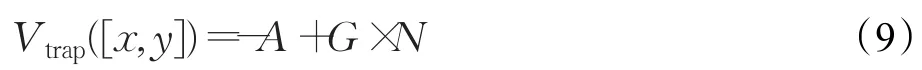
步驟3搜索陷阱起始頂點。從坐標原點沿X正方向進行層內搜索，沿Y方向進行層級搜索，每次移動1個柵格，判斷當前柵格狀態值V([x,y])，左側柵格狀態值V([x-1,y])，上側柵格狀態值V([x,y-1])，如果滿足：

即當前柵格上側和左側均為障礙物，且當前柵格為非障礙物，則認為當前柵格為陷阱區域的起始頂點，將疑似陷阱標志位置1，將當前層疑似陷阱序號加1，記錄當前坐標，轉步驟4；否則不做任何處理，繼續搜索起始頂點。

步驟4繼續沿X右側移動，判斷V([x,y]),V([x,y-1]),V([x,y+d]),V([x+1,y]),若V([x,y-1])＞0,則此處非陷阱區域，置0疑似陷阱標志位，返回步驟3；若V([x,y+d])=-A，為防止將可行路徑識別為陷阱區域而變成不可行域，則認為[x,y+d]為當前疑似陷阱非相鄰障礙物，取消當前層的疑似陷阱標志位，返回步驟3，其中d為可行路徑寬度調節參數。若同時滿足：

即當前柵格處于疑似陷阱，累積當前疑似陷阱中的柵格長度，根據上一層V([x,y-1])的值來判斷當前柵格處于陷阱中的位置，然后轉步驟5：

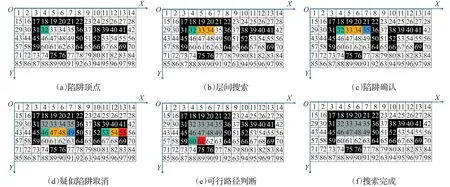
圖2 柵格地圖陷阱搜索流程圖

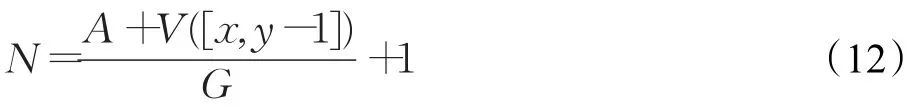
若未能滿足上述不等式，則將當前疑似陷阱排除，清除陷阱柵格長度和所處層級位置，清除疑似陷阱標志位，返回步驟3。

步驟5當沿著當前層疑似陷阱搜索至另一端頂點時，即：

判斷目標位置是否處于當前層陷阱中，如果否，則記錄陷阱序號、起始頂點坐標及陷阱長度。如果目標位置處于陷阱當中，則將當前疑似陷阱排除，清除陷阱柵格長度和所處層級位置，清除疑似陷阱標志位，返回步驟3。

步驟6當一層搜索結束時，根據當前層記錄的陷阱個數、陷阱序號及每個陷阱的長度來更新相應位置的值函數V，并從y+1層再次進行步驟3，直至遍歷整個柵格地圖。

步驟7完成一次遍歷之后，再分別沿X正方向進行層內搜索，Y負方向進行層級搜索；沿Y正方向進行層內搜索，X正方向進行層級搜索；沿Y正方向進行層內搜索，X負方向進行層級搜索；經過4次柵格遍歷，能發現不同朝向的凹形陷阱。

步驟8更新完所有陷阱區域的狀態值函數后，根據當前狀態-動作對(S,a)來更新Q值，即采取動作a后所獲得的瞬時回報值加上當前狀態的最大折扣累積回報V(S)：

如圖2所示為示例柵格地圖的陷阱搜索過程，其中綠色柵格代表疑似陷阱起始頂點，黃色柵格代表疑似陷阱柵格，藍色代表疑似陷阱結束頂點，紅色代表疑似陷阱取消柵格，灰色代表已確認陷阱柵格(d=1)。如圖3為陷阱搜索結束后各柵格的狀態值，陷阱區域狀態值呈現梯度變化。

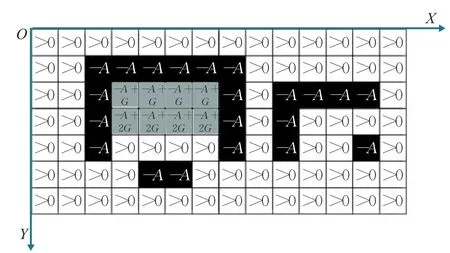
圖3 柵格地圖陷阱搜索完成后狀態值

初始化完成之后，環境地圖狀態-動作值函數有充分的環境先驗信息，采取無障礙物試錯的貪心策略。

回報函數是智能體移動行為的判斷準則，獲得回報越大，則相應的行為策略概率得到提高，回報值越小，則對應的行為策略概率減小。基于Q-learning的常規路徑規劃把到達目標點的回報值設為正數，激勵朝目標方向移動的行為策略，把碰到障礙物的回報值設為負數以懲罰相應的行為。因此，基于此類的路徑規劃方法是從無任何環境認知的狀態進行不斷的試錯，最終收斂Q值查詢表，使智能體以最優的路徑達到目標點[15]。

這樣的試錯策略難以應用到真實的環境中去，對于真實的移動機器人，如果采用無環境先驗信息的試錯學習，會不可避免地撞上障礙物，直接損壞本體，無法進行后續實驗。因此對狀態-動作值函數表的更新進行如下假設：當智能體在隨機探索下預測動作a的下一個環境狀態為障礙物，直接取對應，并按照策略進行下一步動作選擇，由于規定了可探索環境模型的Q(S,a)≥0，每次檢測到障礙物后，將其從可探索環境模型中剔除，在避免了障礙物碰撞的同時，減少了可迭代Q值查詢表，能有效加快收斂速度，并能應用于真實未知環境中的路徑規劃，無需對障礙物設定回報函數值。

5 仿真實驗

采用python編程環境，pygame模塊作為地圖繪制工具進行未知環境下的復雜地圖路徑規劃算法驗證。建立地圖模型尺寸為800×500，最小移動單位為5，智能體動作空間集合A(s)包含前進、后退、左移、右移、左前移、右前移、左后移、右后移8個動作，動作空間集A(s)越大，對應的路徑軌跡越平滑。將地圖劃分為160×100個網格作為環境狀態空間S。以環境地圖的左上角為坐標原點，水平方向為X軸，豎直方向為Y軸建立坐標系，設定起始點和目標點位置如圖4所示：綠點代表初始點，初始坐標為（760，200），藍點代表目標位置，目標坐標為（100，60）。

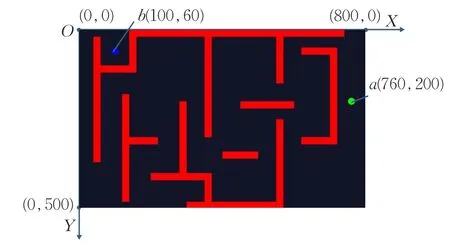
圖4 環境地圖、起始點與目標點坐標位置示意

在確定起始點和目標點坐標之后，進行引力勢場和陷阱搜索初始化Q值函數，將環境的已知信息更新于Q值表之中。圖5所示為進行陷阱搜索之后的環境狀態，其中綠色線條所在區域為陷阱區域，黑色區域為有效探索空間，相比于初始化之前減小了有效狀態空間。其中2號、5號陷阱至外部障礙物之間的距離d由參數調節。

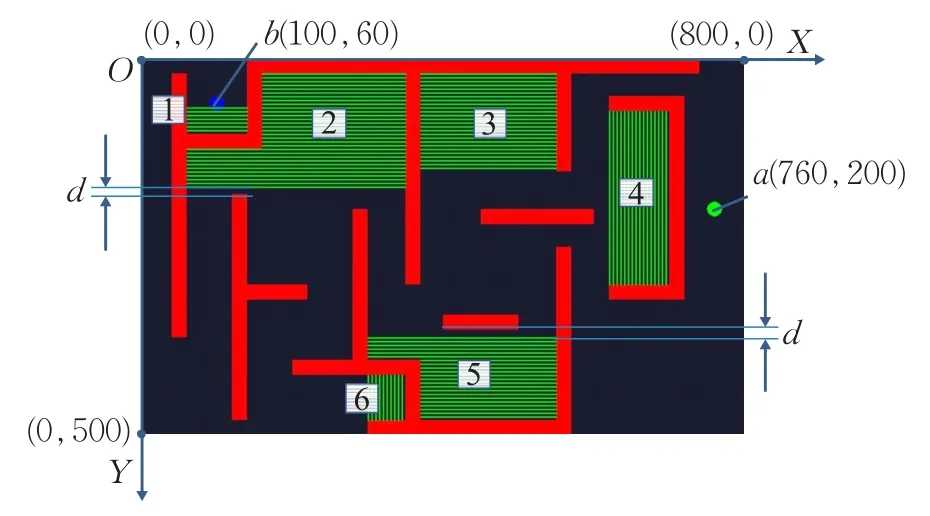
圖5 陷阱區域

為了驗證本文提出方案的有效性，在同一環境地圖下進行3組對比實驗，分別采用常規的不帶有環境先驗信息的Q-learning算法、只應用引力勢場作為環境先驗信息的Q-learning算法和同時應用引力勢場和陷阱搜索作為環境先驗信息的改進Q-learning算法進行路徑規劃，采用相同的折扣率、學習率和ε-greedy法則，每種方法進行2000次迭代，得到最終路徑和起始位置到目標點所需的步數。

通過仿真實驗發現，沒有任何環境先驗信息的強化學習路徑規劃在設定的復雜環境地圖中無法順利到達終點，第一次迭代經過100000步的移動仍然未能到達目標點，即認為在無環境先驗信息且移動路徑不能穿越障礙物的情況下，基于Q-learning的強化學習算法的路徑規劃難以達到目標點，無法完成規劃。

其余兩組方法均能從起始位置到達目標位置，但加入陷阱搜索去掉了較大范圍的路徑搜索，迭代速度明顯快于未加入陷阱搜索的算法，且在初始的若干次迭代過程中，從起始位置到達目標位置所需的步數更少，用時更快。其部分訓練代數路徑規劃效果如圖6和圖7所示，相同的訓練次數圖7的移動路徑優于圖6所示路徑，基于陷阱搜索的環境先驗信息使得智能體在整個訓練過程中不會移動至陷阱區域，提高了算法的效率。

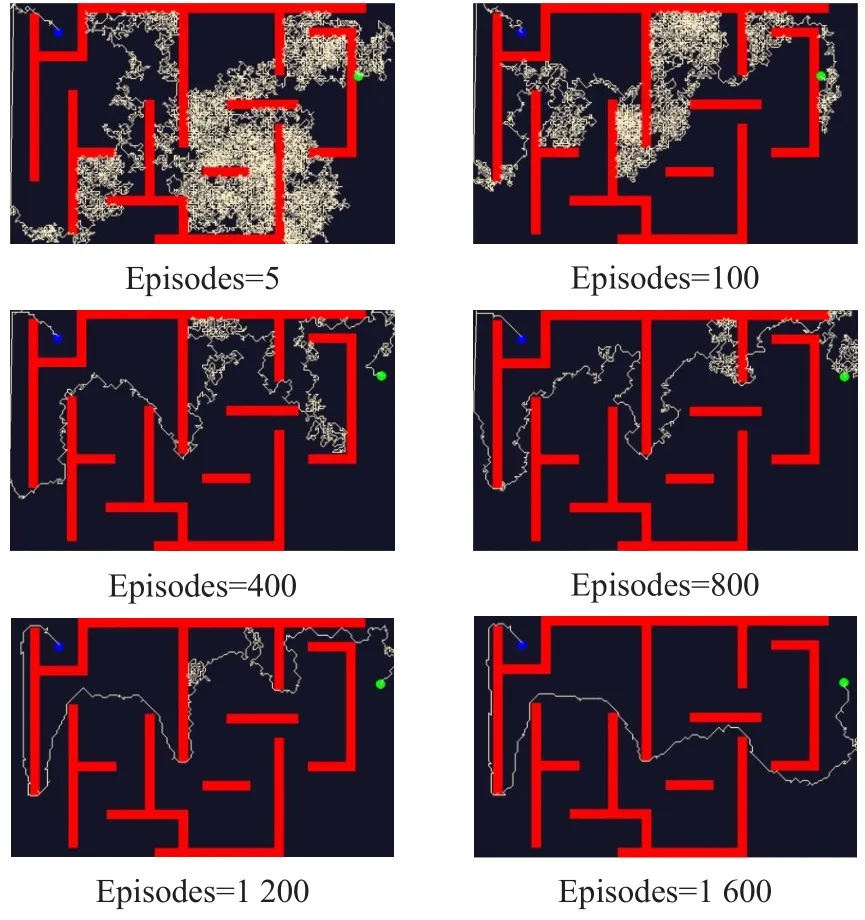
圖6 基于引力勢場的強化學習路徑規劃

將這兩種方法的訓練次數作為橫坐標，每次迭代從起始點到終點所需移動的步數作為縱坐標做圖可得這兩種方法的訓練速度和訓練效果，迭代收斂趨勢如圖8所示。由圖8可知，進行陷阱搜索作為環境先驗信息的路徑規劃訓練效果明顯優于未進行陷阱搜索的路徑規劃，前者收斂速度更快，且在相同的訓練次數下得到的移動路徑短于后者，整個訓練周期時間更短。

6 結論

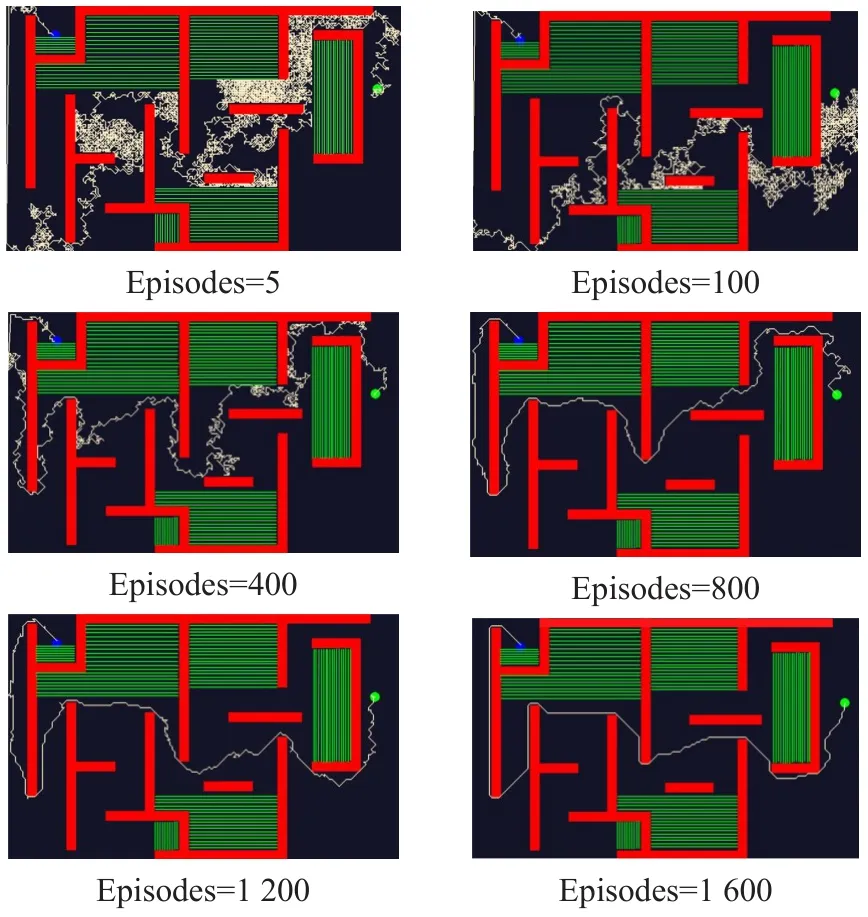
圖7 基于引力勢場和陷阱搜索的強化學習路徑規劃

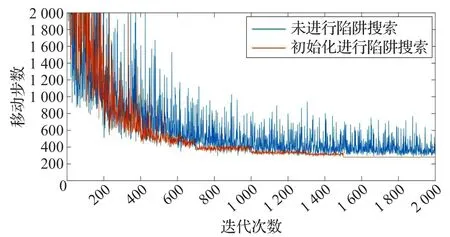
圖8 有無陷阱搜索對路徑規劃迭代影響趨勢圖

傳統強化學習由于訓練速度慢，迭代效率低而難以直接應用。將引力勢場和陷阱搜索聯合作為環境先驗信息初始化Q值函數的強化學習路徑規劃可以得到更快的收斂速度和更優的移動路徑，同時利用初始化避免對障礙物的試錯探索減少了移動體有效狀態空間，在明顯少于傳統強化學習的訓練次數情況下達到更好的路徑搜索效果。對于較為復雜，凹形障礙物較多的環境，傳統的路徑規劃算法不僅計算量龐大，而且易陷入局部陷阱中無法逃逸，本文提出的算法針對此類環境有較高的規劃效率，能找到較優的路徑。