雙混沌和廣義Gray碼相融合的圖像加密算法

謝國波，朱 柳

XIE Guobo,ZHU Liu

廣東工業大學 計算機學院，廣州 510003

School of Computer,Guangdong University of Technology,Guangzhou 510003,China

1 引言

隨著互聯網技術的飛速發展，人們的日常工作以及生活學習開始越來越依賴于網絡。大量信息開始以數字形式進行傳播和存儲。其中，圖片信息因其直觀、生動形象的表現形式，受到了人們的喜愛與推廣。與此同時，由于互聯網的開放環境，網絡上傳輸的一些涉及個人隱私、他人利益、甚至國防軍事等的數字圖像信息必須采取相關密碼學算法可靠加密處理后再進行傳播。數字信息傳播的安全問題一直受到信息安全或者相關領域學者們的廣泛關注，是一個值得深入并長期研究的課題。

圖像信息由于自身數據相關性高、數據冗余度強、數據量大等特點，傳統的針對文本信息的密碼學算法，比如非對稱加密算法（RSA）、數據加密標準（DES）、國際數據加密算法等，并不完全適合圖像加密。而研究結果表明，混沌[1-2]因其初值敏感性、無周期性、偽隨機性、混沌序列的遍歷性等密碼學特性，使其大量被應用于圖像加密中[3-6]。目前基于混沌圖像加密算法普遍都采用像素位置的置亂或像素值替換或者兩者綜合。一些具有代表性的方法，如基于一次一密、位排列、DNA規則、數學模型等的混沌圖像加密算法也同時被學者研究公開。

文獻[7]提出的混沌圖像加密算法基于感知模型，但是由于其密文的不均勻分布，導致該算法不足以抵抗統計攻擊。文獻[8]提出的圖像加密算法基于比特和高維混沌系統，雖然該方法滿足抵抗統計特征攻擊的要求，但是該算法加密所需代價大，效率也相應降低。文獻[9]提出的混沌圖像算法采用一次一密鑰，該算法雖然形式簡單并且具有較高效率，但是不足以抵抗選擇明文（密文）攻擊。文獻[10]提出的混沌圖像加密算法基于DNA序列，然而該算法的加密后像素點相關性較強，存在較大的方差。文獻[11-12]中鄒建成、宋莉莉等人對廣義Gray碼及其在數字圖像加密中的應用進行了分析闡述，證明了廣義Gray碼在圖像加密算法中的應用前景。

本文提出了雙混沌和廣義Gray碼相融合的圖像加密算法，通過該算法進行加密的密文圖像不僅與明文緊密關聯，也起到了良好的置亂擴散效果。實驗結果表明，本算法具有良好的統計性能、足夠大的密鑰空間、明文（密文）敏感等優良性能。

2 算法原理

本文加密算法的整體原理如圖1（a）所示。

圖1 加密/解密流程

2.1 混沌系統及廣義Gray碼

2.1.1 Kent混沌映射

Kent映射是一個性能很好的混沌系統，其映射關系為：

式（1）中，S為混沌系統的控制參數。當x∈(0,1),S∈(0,1)時，式（1）具有一個正的Lyapunov指數，此時Kent映射將處于混沌狀態，由此初始條件x0在Kent映射中產生的序列具有很好的自相關性、互相關性和平衡性等偽隨機性能。同時，Kent映射對初始條件極為敏感，即使初始條件發生極其微小的變化，其產生的隨機序列也將會完全不同。利用這一特性，Kent映射被良好地運用在混沌圖像加密中。

2.1.2 Logistic混沌映射

Logistic映射是一個經典的一維離散混沌動力系統，它的誕生來源于人口統計，其具體規律可用如下數學公式（2）定義：

其中，μ為系統非線性強度的參數，取值范圍為0≤μ≤4；k為混沌系統的迭代次數；xk為Logistic混沌系統的初始值，取值范圍為0＜xk＜1。當3.569≤μ≤4，該系統映射處于混沌狀態，此時對初值的微小改變都會導致系統產生完全不同的非收斂、非周期性的序列。

2.1.3 廣義Gray碼

（1）對于任意的非負整數u，其二進制碼記為u=(upup-1…u0)q，令

其中i=1,2,…,p，則可得到一個二進制表示的整數g(u)=(gpgp-1…g0)q。

上述變換稱為Gray變換g(u)稱為u的Gray碼，其中運算“⊕”為模2加法。

（2）對于非負整數u，其q進制碼記為u=(upup-1…u0)q，定義如下變換：

其中，q≥2為正整數；aij為整數，i,j=1,2,…,p-1。當系數矩陣的行列式|(aij)|與q互為素數時候，則該變換符合u的廣義Gray變換，g(u)=(gpgp-1…g0)q稱為廣義Gray碼。

2.2 加密與解密原理

本文所提出的數字圖像加密基于典型的“置亂-替換”結構，首先對原始圖像進行分塊，接著通過Kent映射進行重排列，然后再次利用Kent映射產生一維混沌序列對重排列后的圖像進行全局位置置亂，接下來再采用Logistic映射和廣義Gray碼對位置置亂后的圖像像素值進行替換完成整個加密過程。

2.2.1 圖像的位置置亂

像素位置置亂的目的是通過打亂圖像像素點原始位置來破壞相鄰像素點之間的相關性。其具體的實施步驟如下：

首先對圖像進行分塊，假設待加密圖像I的大小為a×b，分塊的具體步驟為：

步驟1將圖像I的像素矩陣按照行和列進行等長劃分，設置劃分的大小分別為j和k，其中：

具體的劃分規則如下：

規則1當mod(a,j)=0，mod(b,k)=0時，圖像I則被劃分為j×k塊，每塊的大小為

規則2當mod(a,j)≠0，mod(b,k)=0時，圖像I則被劃分為兩類不同的塊，一類塊大小為，另一類塊的大小為

規則3當mod(a,j)=0，mod(b,k)≠0時，圖像I則被劃分為兩類不同的塊，一類塊大小為，另一類

規則4 當mod(a,j)≠0，mod(b,k)≠0時，圖像I則被劃分為四類不同的塊，一類塊大小為一類塊的大小為，一類塊的大小為最后一塊的大小為mod(a,j)×mod(b,k)。

步驟2對分塊進行重新的組合排列。

首先將Kent映射迭代1000次以消除暫態效應，從第1001次開始記錄產生長度為j×k（用規則1的分塊個數進行示例說明）的混沌序列H={h1,h2,…,hj×k}。對混沌序列進行升序排列，記錄排序后的各元素在原始序列H中的位置，生成新的序列利用序列H′對分塊進行置亂。

假設分塊為B={b1,b2,…,bj×k}。其置亂規則按照如下公式：

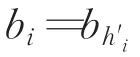
置亂前后如圖2所示。然后對分塊后圖像的像素點進行全局置亂。

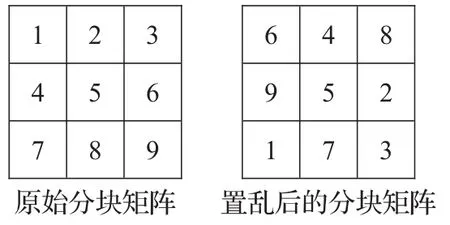
圖2 分塊前后的排列對比

步驟1對待加密的圖像明文按照行（列）優先的順序掃描，轉化成為長度為a×b的一維序列I={i1,i2,…,im×n}。

步驟2對明文圖像的像素值sum進行求和運算，分別運用式（7）和式（8）求出混沌系統的混沌參數S和混沌系統的迭代次數c：

步驟3結合步驟2得出的混沌參數S，對混沌系統設置一個初始值x1，將參數S和初始值x1代入到式（1）中。Kent映射迭代c次以消弱暫態效應的不良影響。接下來再迭代a×b次產生一個長度為a×b的混沌序列L={l1,l2,…,la×b}。運用排序算法對混沌序列進行升序（降序）排列L′={l′1,l′2,…,l′a×b}，計算序列L中的各值在序列L′中的位置，從而生成一個記錄順序序列中各元素在原序列L中新的位置的序列w={w1,w2,…,wa×b}。

步驟4利用序列w來置亂明文圖像I，置亂的依存規則為l′i=lwi，置亂后的序列記錄為：

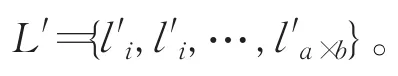
2.2.2 像素值的替換

此階段使用Logistic映射和二進制的廣義Gray碼對位置置亂后的圖像I′進行像素值替換。

步驟1設定混沌系統的初始值x3、x4，以及系統參數λ。將上述系統參數和初始值代入Logistic映射中，迭代1000次以消除暫態效應，從第1001次開始進行記錄，生成兩個長度大小為a×b的混沌序列：

M={m1,m2,…,ma×b}，N={n1,n2,…,na×b}

步驟2將序列M中的各序列值代入式（9）進行轉化，讓其值域控制在[0，255]之間，新產生的序列更改為T={t1,t2,…,ta×b}。

步驟3對序列N中的序列值進行升序（降序）排列，生成序列N′={n′1,n′2,…,n′a×b}，記錄下序列N′中的值在原始序列N中的下標值，生成新的序列Y={y1,y2,…,ya×b}。

步驟4將位置置亂后的圖像各像素值I={i1,i2,…,ia×b}與序列T進行異或操作，其異或公式如下：

步驟5將步驟4異或后所得的像素點的像素值按照廣義Gray碼的替換公式（11）和（12）進行替換。當u=(un-1un-2…u0)2時，其對應廣義Gray碼。

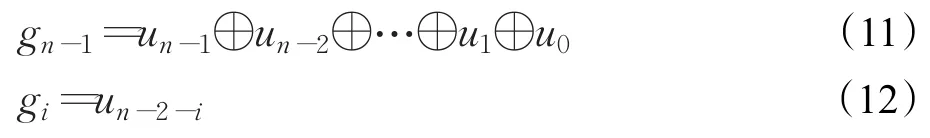
通過變換產生一個新的二進制編碼：

g=(gn-1gn-2…g0)2

以上步驟即為加密的全部過程。

2.3 解密原理

解密過程即為加密過程的逆過程，依次對替換和置亂階段進行逆向操作處理。

首先，將密文圖像V按照行（列）優先進行展開生成一維序列，將序列中的各個點的像素值按照廣義Gray的生成規則進行運算得到序列V′，再對序列V′按照公式進行異或，得到位置置亂后的序列。最后對置亂后的序列進行反置亂即可得到明文序列P，將得到的一維序列轉化為二維矩陣即為加密前的明文圖像I。

3 實驗結果及性能分析

3.1 算法仿真

本文仿真過程采用的圖像為經典的lena灰度圖像，其大小為256×256。其中加密系統的初始密鑰有Kent映射的初始值x1=0.3467832426，x2=0.5467832426和Logistic混沌映射的初始值x3=0.2467832426,x4=0.4467832426。其中Kent映射的控制參數由明文圖像自身決定，Logistic映射的控制參數自行進行設定，本次仿真實驗將其設置為λ=3.9467832426。其加密前后的效果圖對比如圖3。

圖3 明文與密文圖像

3.2 算法的統計特性分析

3.2.1 直方圖分析

直方圖即為圖像的灰度值分布圖，它所展示的是圖像像素值的分布情況。

圖4的灰度直方圖中展示的分別為原始圖像和加密后圖像的直方圖。從圖4（a）中可以明顯發現，加密前的直方圖分布起伏較大且不均勻分布，而運用本文算法進行加密后的直方圖圖4（b）則呈現均勻分布。

為了進一步確定算法密文直方圖均勻性，采用式（13）計算并分析。其中z是密文圖像各灰度級別下的像素統計值，(zi,zj)分別是灰度值為i和j的像素統計值。采用不同密鑰對圖像進行加密處理，然后對產生的密文計算方差。計算所得的方差值越小，則表示生成的密文直方圖越均勻，所產生的直方圖在直觀上越平滑。

表1 密文直方圖的方差

圖4 灰度直方圖

本文選取原始密鑰(x1,S,x2,k,μ)作為初始密鑰key1，通過改變原始密鑰中的某一個參數值來分別產生多張密文。實驗過程中另外引入256×256的Cameraman圖像與Lena圖像進行對照。與文獻[5]相比，結果如表1所示。通過對以上不同的密文圖像的實驗分析，發現加密后的密文平均各灰度級的像素數目在70，方差在5000上下，而其明文圖像的方差值則為密文的10倍以上。

3.2.2 相鄰像素相關性分析

對加密前后的圖像分別選取2200組的相鄰像素點來進行分析，公式如下：

其中，rx,y為相鄰像素點的相關系數；x和y分別代表相鄰像素點像素值。將選取的2200組明文和密文的像素點運用關系圖表示出來。原始圖像圖5（a）顯示出來的像素點表明水平相鄰點的像素值比較接近。密文圖像圖5（b）顯示出來的像素點表明水平相鄰點的像素值差異明顯。運用公式分別對明文圖像和密文圖像的水平、垂直、對角所有點的像素值相關性進行計算，并且與文獻[13-15]進行比較，其具體結果如表2所示。

圖5 明文/密文的相關性

表2 密文圖像相關性系數

對比加密前后相關性系數，加密后的圖像的像素點相關性接近于0，相鄰元素之間基本沒有相關性。而明文圖像的相關性接近于1，說明該算法很好地抵抗了統計分析，具有良好的加密效果。

3.3 經典攻擊分析

經典的攻擊方法有已知明文攻擊、唯密文攻擊、選擇明文（密文）攻擊[16-17]。

明文攻擊是指在獲得明文的情況下破解算法的概率。唯密文攻擊是指僅知道密文的情況下破解算法。而選擇明文（密文）攻擊所指的是攻擊者通過選擇一組標定的明文（密文），通過對該加密系統的使用來同步獲取對照的密文（明文），對密文進行分析獲取中間密鑰，通過獲得的中間密鑰從而完成對明文的解密。

目前混沌加密算法普遍采用的是基于位置置亂和像素替換的加密過程。由于Logistic映射參數空間有限，而且在計算機有限精度下容易出現動力學退化，因而會被破解，而針對該過程所常用的攻擊方法就是選擇明文和選擇密文攻擊。這里最常見的攻擊思路為選擇一個與密文圖像相同大小的像素值全部為0的圖像進行破解得到中間密鑰。然后選取該圖像的某個像素點進行標記，通過對標記像素點的追蹤記錄，獲取該像素點的初始位置，破解明文圖像。

但是以上破解方法針對本文所描述算法是不可行的，在像素的位置置亂階段，無論是分塊階段還是全局置亂階段，其Kent混沌映射的參數都是由明文圖像的像素總和Sum和像素大小a、b共同決定的，而上述方法中所運用的圖像像素值為全0，從而使得其產生的混沌序列也不盡相同，無法取得映射參數，因此直接導致的結果就是無法獲得中間密文。另外，在像素值替換階段才采用Logistic映射，利用預設的初始密鑰x3，通過x3產生的混沌序列進行排序生成新的下標序列，利用該下標序列進行像素值之間的異或操作。在未獲得準確x3的前提下，攻擊者是無法確定中間密文的，因此對于選擇密文攻擊無效。綜上所述，本文設計的圖像加密算法能夠很好地抵抗以上攻擊方式。

3.4 抗差分攻擊性能分析

3.4.1 密鑰敏感性分析

密鑰的敏感性指的是當密鑰發生極其微小變化時，對圖像的加密（解密）也會產生顯著影響。在對明文圖像進行加密時，將Kent映射或者Logistic映射的初始值進行微小改變，固定其他的參數和系統初始值，最終解密也無法獲得正確的明文圖像。實驗仿真中，將初始值x1=0.3467832426變為x1=0.3467832427。圖6（a）為解密后的圖像。同等情況下，改變x3，圖6（b）為解密圖像。由上可知，該加密算法具有良好的密鑰敏感性。

圖6 改變密鑰后的解密圖像

3.4.2 明文敏感性分析

明文的敏感性指的是明文的變化對密文的影響比重，它是衡量一個算法抵抗差分攻擊性能的重要指標。在常用的攻擊方法中，廣泛采用的是在微小改變明文的情況下來分析密文變化特征，從而找出規律破解密文。本算法由于在密鑰的生成過程中引入了像素和以及圖像二維矩陣的行數和列數，使得密鑰與明文密不可分。

常用像素改變率（NPCR）和歸一化平均改變幅度（UACI）來衡量密文對明文的敏感性。令I1和I2分別為兩個明文圖像加密后的密文圖像，其中I1是圖像I的加密圖像，I2是圖像I在某個像素點發生變化后的密文。設兩幅密文圖像在相同位置(i,j)的像素值分別為p1(i,j)和p2(i,j)。當p1(i,j)=p2(i,j)時，定義H(i,j)=0；若p1(i,j)≠p2(i,j)，定義H(i,j)=1。

NPCR與UACI的計算公式分別為：

根據上述原則，在lena圖像中任取一點對其像素值進行改變，例如在位置（11，29）處，將其值由47變為48，根據式（18）和（19）可以計算出NPCR=99.61%，UACI=33.46%。因此，該算法滿足密文圖像對明文圖像微小變化的敏感性，足以抵抗攻擊者的差分攻擊。

3.5 密鑰空間分析

足夠大的密鑰空間是用來評價一個算法能否抵抗窮舉攻擊的基本標準。在本文所描述的算法中，雙混沌系統的迭代初始值以及Logistic映射的參數都可以用來作為密鑰。在64 bit計算機中，每個double類型的有效位能達到16位。這樣，即使攻擊者采取每秒億個密鑰進行窮舉攻擊，所需要的時間也遠遠導致其不可實現性。如果再把迭代次數、分塊等加入密鑰中，密鑰的空間將會更加巨大，所需要的時間也更長。因此，本文算法的密鑰足以抵抗窮舉攻擊。

4 結束語

本文提出的是雙混沌和廣義Gray碼相融合的圖像加密算法，該算法采取經典的置亂-替換結構進行加密。本文算法不僅保留了“置亂-替換”算法原本的優點，同時也采取相應技巧避免受非法攻擊。本文算法所具有的特點如下：

（1）在進行像素置亂過程中，不同于傳統大多數算法，本文算法首先對圖像進行分塊處理，然后再對重排列后的圖像進行全局置亂，使得算法置亂效果更好。

（2）Kent映射的系統參數由明文圖像的自身特性來決定。因此不同的明文圖像所采取的控制參數也不盡相同，從而生成的混沌序列也完全不同，使得算法具有抵抗選擇明文（密文）能力。

（3）利用Logistic生成的混沌序列，同時采取對應的數學公式來對像素值進行擴散操作，不僅使得像素值的替換具有較好隨機性，同時也一定基礎上增加了系統抗攻擊的能力。

（4）利用廣義Gray進行二次擴散，進一步提高加密圖像的安全性。

實驗仿真結果表明，本文算法不僅具有良好的加密效果，而且具備較好的安全性。