未知時變慣量航天器自適應姿態跟蹤容錯控制

高 直，陳 偉，邵 星

GAO Zhi,CHEN Wei,SHAO Xing

鹽城工學院 信息工程學院，江蘇 鹽城 224051

College of Information Engineering,Yancheng Institute of Technology,Yancheng,Jiangsu 224051,China

1 引言

隨著航天事業的不斷發展，航天器在執行在軌維護、對地觀測和深太空探索等航天任務時，要求姿態快速并準確地對參考姿態進行跟蹤控制[1-3]。近年來，航天器的姿態跟蹤控制問題引起了眾多學者的廣泛關注，并就此展開了大量的研究。目前，國內外學者在該領域取得了大量的姿態控制理論研究成果，如自適應控制[4-7]、反步法[8-11]、滑模控制[12-15]、有限時間控制[16-19]等方法。

由于太空環境的復雜性，在軌運行的航天器在工作過程中不可避免地會受到外界力矩干擾，這些干擾力矩主要包括太陽光壓及重力梯度。此外，由于太陽帆板運動和液體晃動，航天器的慣量會發生未知變化，以及無法準確獲知航天器慣量參數信息[4]。對于存在外界干擾和轉動慣量不確定性的剛體航天器姿態控制問題，文獻[4-6，8，10-12，16，18，20]對此進行了研究。文獻[4]基于魯棒控制、自適應控制和輸出調整理論，提出了一種自適應內模方法，實現了姿態跟蹤系統的全局穩定。針對存在未知轉動慣量和外部干擾力矩的航天器快速大角度姿態機動問題，文獻[5]結合非線性反步法和Lyapunov穩定性分析方法設計了帶有轉動慣量估計值的非線性魯棒自適應控制律，并證明了姿態機動系統最終一致有界穩定。文獻[6]基于自適應反步法和非線性阻尼算法，提出了一種魯棒自適應控制器，實現了對慣量參數的估計，并且克服了外界干擾，最終保證航天器姿態控制系統全局一致最終有界穩定。文獻[11]針對航天器姿態穩定控制問題，設計了一種迭代學習控制方法，分別對外界干擾和緩慢且小幅變化的不確定性構建有界學習控制律，進而給出航天器穩定控制律，實現了姿態跟蹤誤差有界穩定。文獻[20]研究了模型參數不確定性因素下的航天器姿態機動問題，設計了一種保性能控制律，在補償參數不確定性的同時還能滿足系統性能指標的要求，使得航天器在不確定性的影響下能夠精確完成大角度姿態機動，在此文中，外界干擾影響未作考慮。

伴隨著航天任務的多樣性和復雜性，航天器對執行機構的安全性和可靠性要求越來越高。由于航天器長期工作在高低溫、失重和強輻射的惡劣環境下，以及長時間的工作，機載元器件會逐漸老化，最終導致執行機構產生功能衰退等故障，進而影響系統的穩定性，隨之，航天器的容錯控制問題成為近幾年的一個研究熱點[21-24]。文獻[22-23]在慣量設定為定常的條件下考慮系統容錯控制問題。文獻[22]針對執行機構損失部分效能的情況，設計了一種自適應反步控制策略，使得航天器在外界干擾的環境中達到姿態穩定。文獻[23]在不考慮外界干擾的情況下，針對執行機構功能衰退故障設計了一種自適應容錯姿態控制邏輯。文獻[24]針對具有未知常數慣量不確定性和外界干擾的航天器，設計了一種有限時間自適應滑模姿態跟蹤控制器，使得期望姿態能夠在有限時間內被跟蹤上。航天器執行任務時，由于受燃料持續消耗、液體晃動、太陽帆板運動等客觀因素影響，航天器慣量是未知時變的[25-28]。

通過上述研究成果分析，以上容錯控制策略并沒有同時考慮時變慣量和執行機構損失部分能量情況下的航天器姿態容錯控制問題。受上述問題啟發，本文針對非剛體航天器在軌運行時受到慣量未知時變性、外界持續干擾以及執行機構部分失效問題，設計了一種自適應姿態跟蹤容錯控制律，使得航天器在執行機構發生部分失效故障時依舊能夠使得航天器姿態跟蹤上期望姿態。所提的控制律結構簡單，易于工程實現，理論分析和數值仿真驗證了該控制策略的有效性。此外，該方法可同時用于剛體航天器的自適應姿態跟蹤容錯控制，在控制律設計部分已對此進行說明。

2 問題描述

2.1 航天器數學模型

非剛體航天器的姿態運動學和動力學方程[28]為：

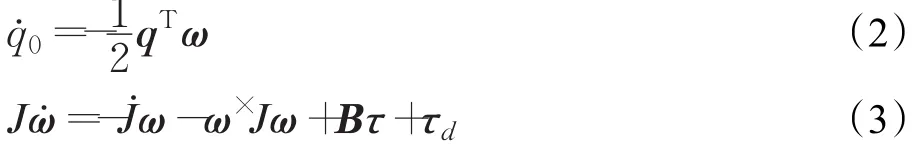
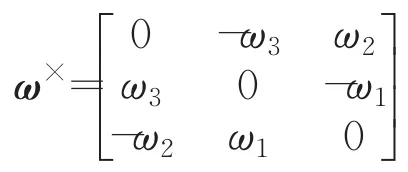
注1在剛體航天器動力學模型中，參考文獻[1-27]，-J?ω因子是不存在的。

圖1為航天器坐標示意圖，航天器繞慣量坐標軸旋轉的歐拉角分別為滾轉角φ、俯仰角θ和偏航角ψ。XIYIZI為慣量坐標系，XBYBZB為本體坐標系，從慣量坐標系到本體坐標系采用3-2-1的旋轉順序，即按照ZY-X軸的順序旋轉。首先繞Z軸旋轉角度ψ，其次繞Y軸旋轉角度θ，最后繞X軸旋轉角度φ。由于采用歐拉角描述存在奇異問題，且需多次三角運算，而采用四元數描述可以避免此類問題，同時，歐拉角轉換為四元數是一對一的關系，運算簡單，因此工程上普遍采用四元數描述航天器的運動及動力學中的姿態。四元數與歐拉角之間的轉換關系可參考文獻[5]中式（7）。ω為本體坐標系相對于慣性坐標系的旋轉角速度。

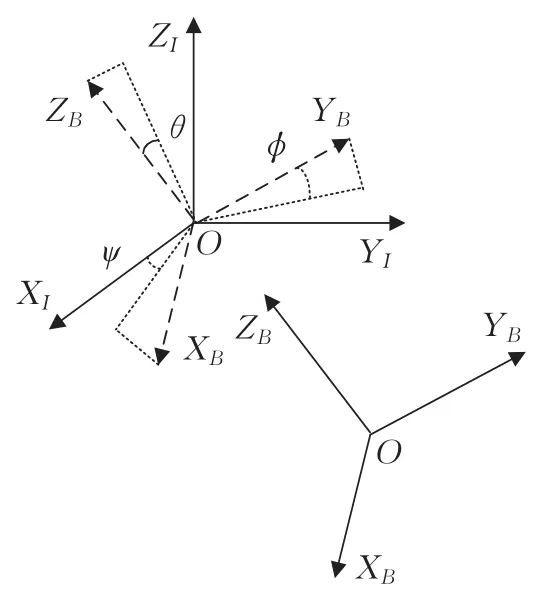
圖1 航天器坐標示意圖

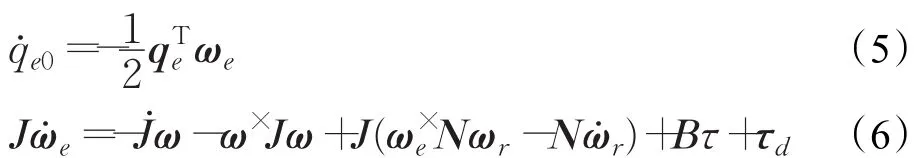
注2由于燃油消耗和液體晃動等因素導致慣量變化，慣量矩陣可進行合理性假設：航天器在工作過程中，Ji是正定有界的及是有界的。

2.2 控制目標

針對非剛體航天器使用過程中存在未知時變慣量不確定性、位置外界干擾及執行機構衰退故障等因素，設計一種自適應容錯控制，使得航天器姿態及角速度誤差系統一致有界穩定，即a2，其中，a1、a2為非常小的常數值。

3 控制律設計及穩定性分析

3.1 自適應容錯控制律設計

為了便于后面的控制律設計，首先定義一個誤差輔助變量S：

對式（7）求導可得：

其中，β是一個正實數。

由于外界干擾、慣量及其一階導數是有界的，可以得到：

針對系統存在外界干擾和慣量時變不確定性參數，首先利用自適應參數估計外界干擾上界和慣量時變不確定參數，其次利用自適應參數和誤差輔助變量進行控制器設計，最終使系統達到一致有界穩定。

本文所提出的未知時變慣量航天器自適應姿態跟蹤容錯控制律原理如圖2。

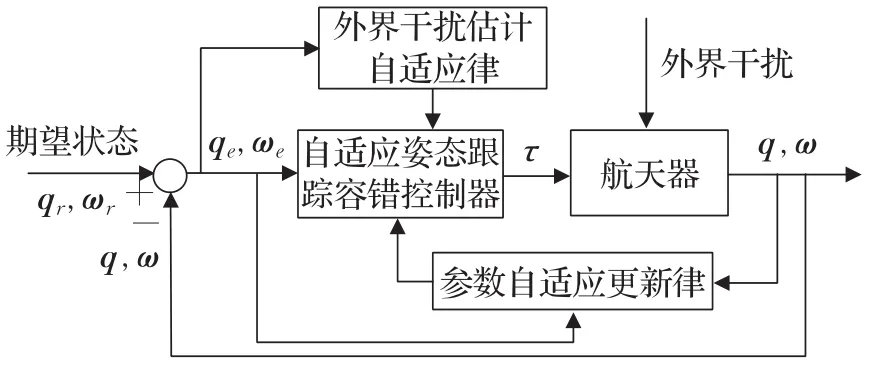
圖2 自適應姿態跟蹤容錯控制原理

根據圖2所示控制原理，設計自適應容錯控制律為：

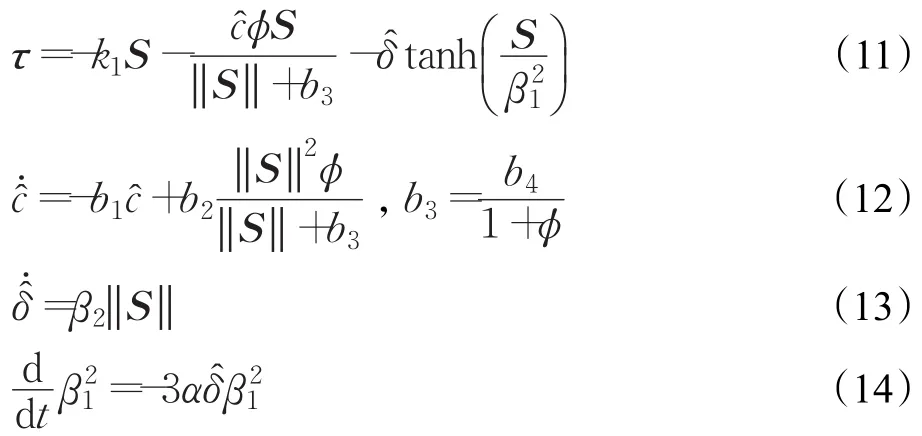
其中，k1、b1、b2、b4、β2和α是正常數，β1是時變的且滿足β1()

0＞0；參數?是抑制慣量不確定性的自適應參數；?是外界未知干擾最大值的估計值。式（12）～（14）是自適應更新律，根據未知時變慣量和外界干擾對系統的影響進行自適應更新。

注3相比文獻[5]中控制方法，該控制律沒有對慣量進行單獨估計、相應的變量變換以及矩陣Y的計算，控制結構簡單，易于工程實現。

注4對于剛體航天器[1-27]，動力學模型表達式中不存在-J?ω項。因為是有界的，所以不等式（10）仍舊成立。進而，控制律（11）及自適應律（12）～（14）適應于剛體航天器。

為了便于后面穩定性證明，引入以下引理。

引理1[27]對于任意實數x和非零實數y，都有下面不等式成立：

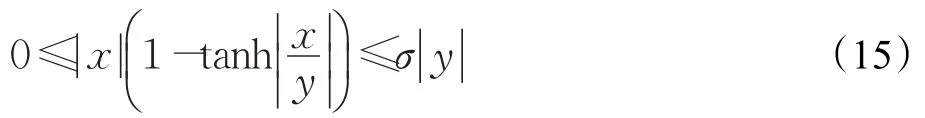
其中，σ＞0，σ的最小值σmin滿足σmin=x*(1-tanhx*)，x*滿足方程e-2x*+1-2x*=0。

3.2 系統穩定性分析

針對3.1節提出的自適應容錯控制器，利用Lyapunov方法進行系統的穩定性分析。

定理 考慮存在未知時變慣量不確定性、持續外界干擾以及執行機構衰退故障的非剛體航天器系統（1）～（3），若采用控制律（11）和自適應律（12）～（14），則航天器誤差系統（4）～（6）是一致有界穩定的。

證明 選取Lyapunov函數為：

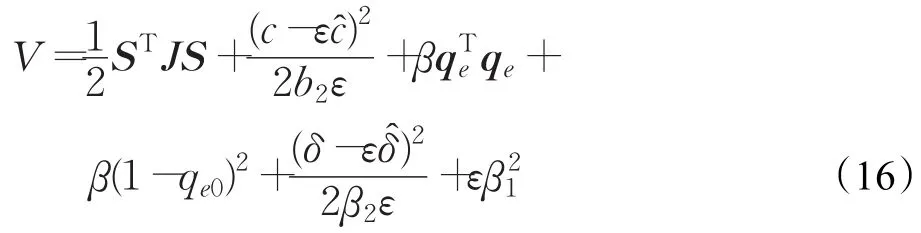
其中，ε=min(μ1,μ2,μ3) 。

對Lyapunov函數求導并由式（4）～（10）得：

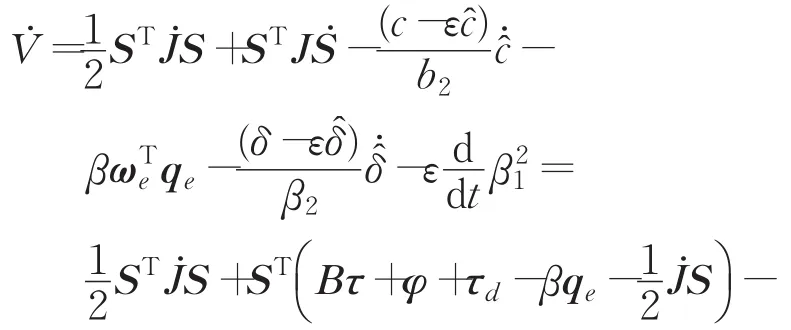
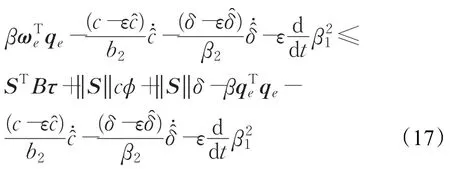
把控制律（11）及自適應律（12）～（14）代入式（17）得：

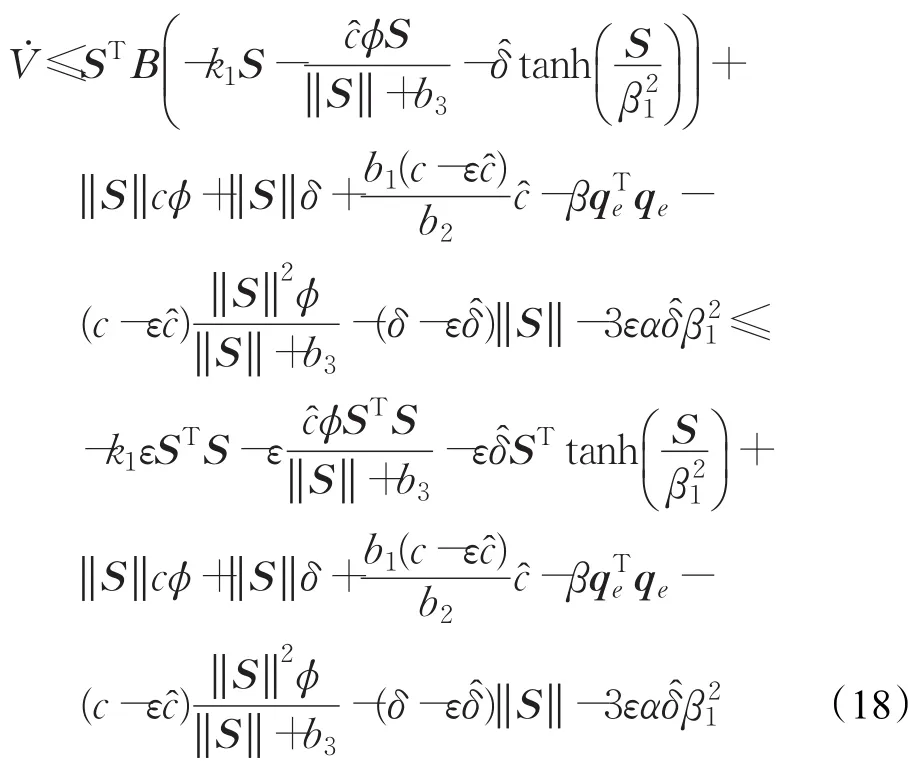
通過引理1可以得出：

由式（20）可以推導出：

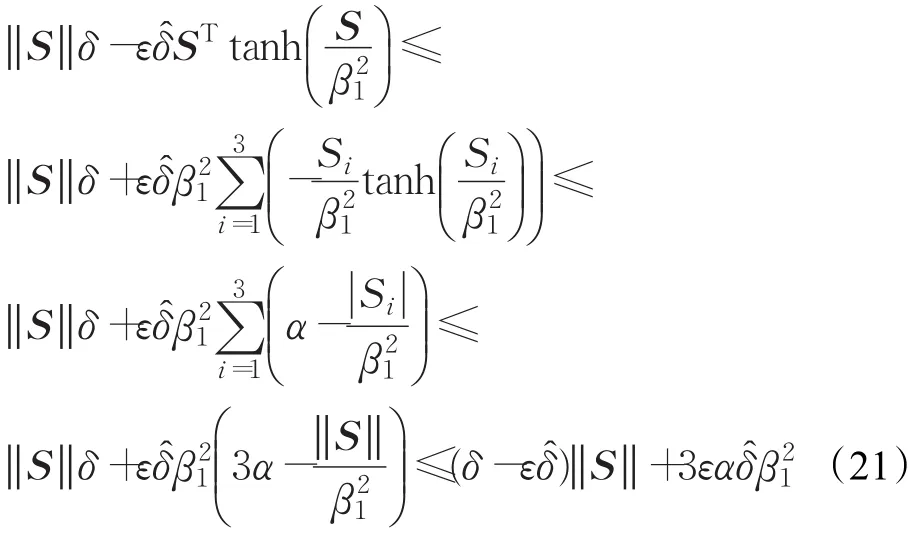
同時：

把式（21）～（22）代入式（19）得：

航天器時變慣量矩陣及初始姿態值見表1，初始角，由式（23）可得誤差集：

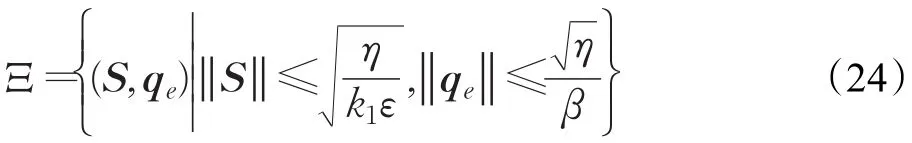
由式（24）可以得出參數k1、b2數值越大，及b1、b4數值越小，則航天器姿態跟蹤系統（4）～（6）穩態誤差越小，即控制精度越高，實現跟蹤誤差系統最終一致有界穩定[29]。

4 仿真驗證與比較

4.1 仿真驗證

為了驗證本文提出的控制器對航天器姿態穩定控制的有效性和魯棒性，在此給出仿真參數進行數值仿真。

航天器的期望軌跡：

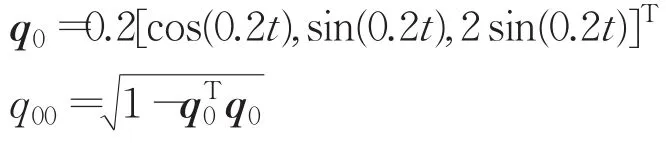
角速度可通過式（2）獲得。

外界干擾τd=0.5[0.02sin(t),0.05cos(t),0.03cos(t)]T。執行器效率矩陣B=diag(0.6+0.2sin(t),0.8+0.2cos(t),0.7+0.2sin(t))。控制器參數k1=20，β=1，b1=0.01，b2=60，b4=0.1，β2=0.1，α=0.3。自適應參數初始值速度值

注5為模擬時變慣量矩陣，采用慣量初始值乘以因子cos(0.05t)，仿真時間為[0,20]s。

圖3及圖4給出了航天器姿態及角速度跟蹤誤差曲線。從圖中可以看出在控制律（11）及自適應律（12）～（14）作用下，盡管非剛體航天器受到執行機構衰退故障、未知時變慣量不確定性及外界干擾影響，仍能很好地完成姿態跟蹤任務，跟蹤誤差最終趨于零點附近一個很小的鄰域內，控制器具有很好的控制效果。圖5為控制器輸出力矩，實際作用在航天器的力矩為此輸出力矩乘以執行機構效率矩陣B。圖6～圖8為控制器自適應參數數值變化曲線。

表1 慣量矩陣和初始姿態

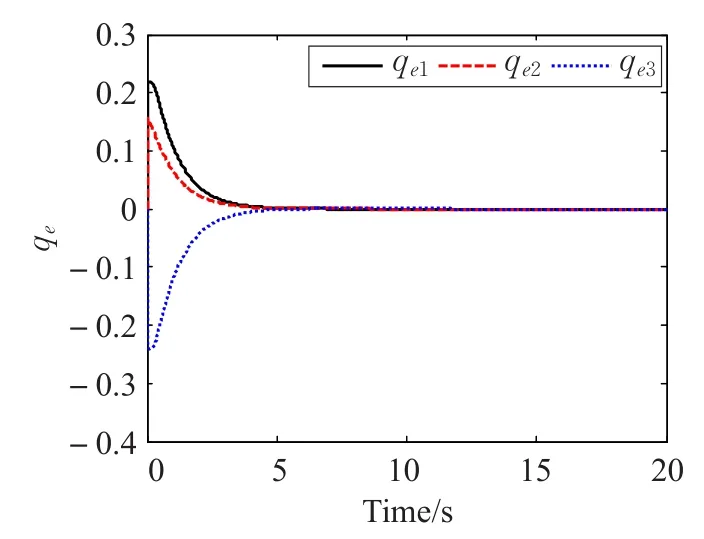
圖3 姿態跟蹤誤差曲線

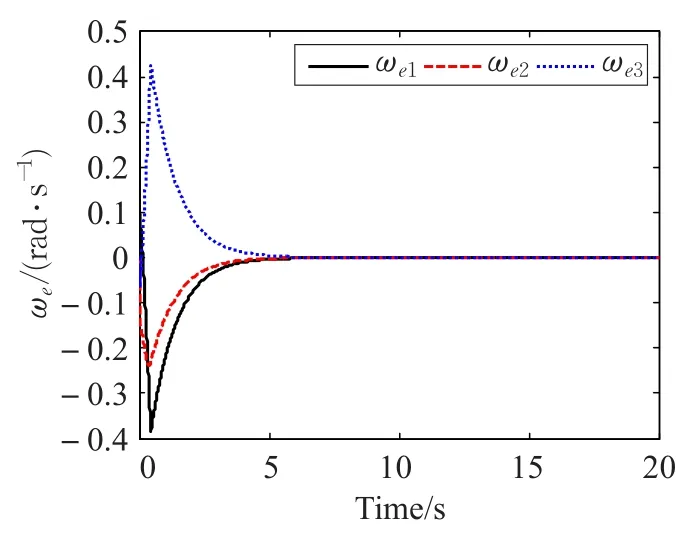
圖4 角速度跟蹤誤差曲線

圖5 控制力矩曲線

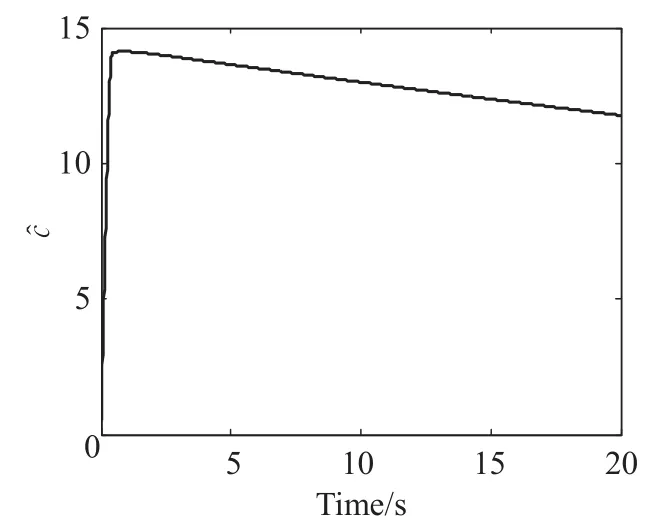
圖6 參數c估計值曲線

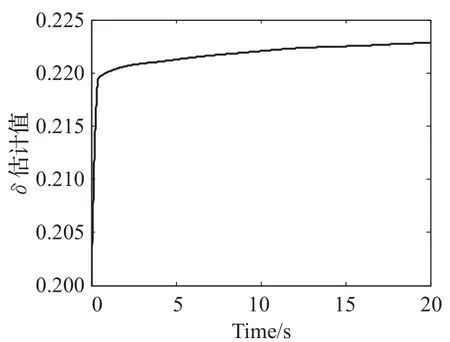
圖7 外界干擾估計值?曲線

圖8 參數變化曲線

4.2 仿真對比

為驗證不同干擾形式下本文方法的有效性及更高的控制精度，外界干擾選取不同于4.1節的形式τd=[0.1+0.2sin(t),0.4+0.5cos(t),0.2+0.3cos(t)]T,同時與文獻[26]進行仿真對比，仿真對象為剛體航天器，即動力學方程（3）中不包含-J?ω項。慣量矩陣、執行器效率矩陣及期望軌跡與4.1節相同。文獻[26]控制器參數選取與所提控制器參數值相同，即k0=k1=20,β=1,σ1=b1=0.01,σ2=b2=60,μ=b4=0.1。由本文方法和文獻[26]自適應姿態容錯方法所產生的曲線分別用“Proposed”和“Comparison”標注。圖9和圖10分別表示姿態誤差范數和角速度誤差范數曲線圖。從圖中可以看出，姿態及角速度跟蹤誤差在8 s時可以達到3×10-3，本文方法誤差可以達到2×10-3，控制精度更高，并且在不同的干擾模式下仍舊可以快速地使系統達到穩定狀態。

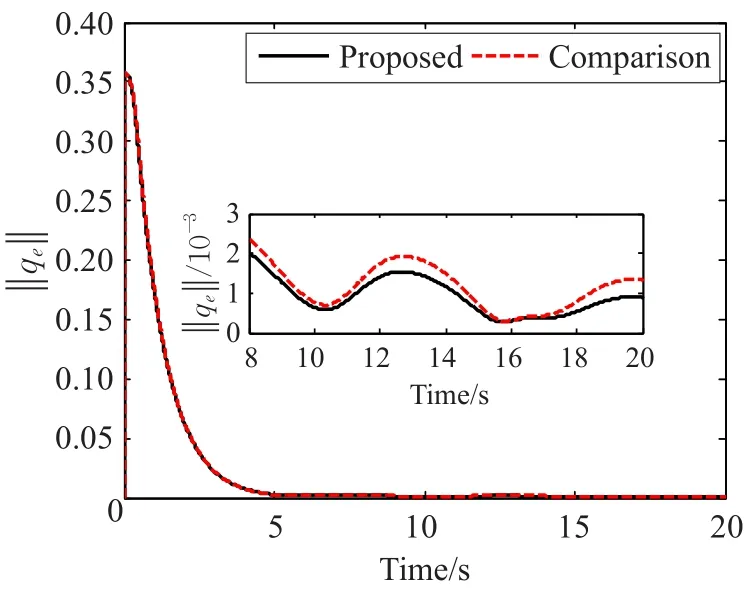
圖9 姿態誤差范數‖‖變化曲線

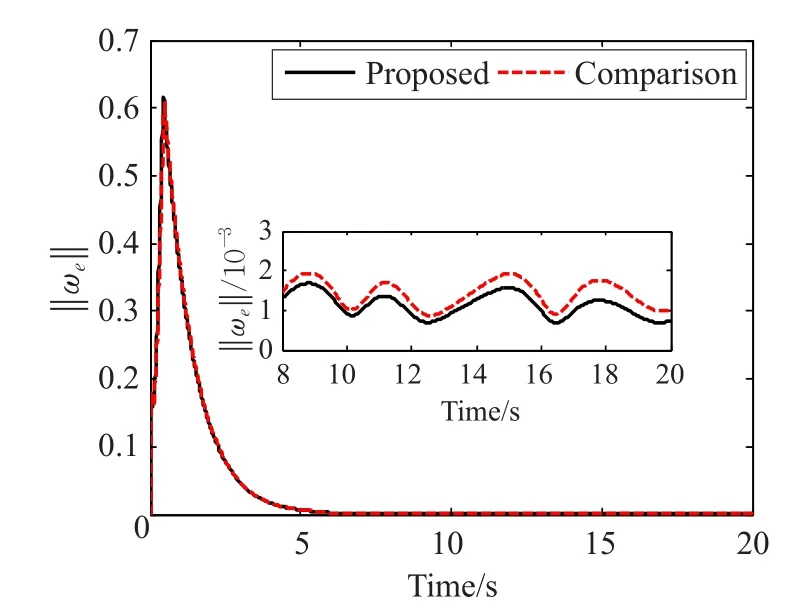
圖10 角速度誤差范數‖‖變化曲線

5 結束語

本文研究了同時存在執行機構衰退故障、未知時變慣量不確定性及外界干擾的非剛體航天器姿態跟蹤誤差系統穩定性控制問題，基于非線性系統魯棒控制方法、自適應方法及參數估計方法，設計了一種自適應姿態跟蹤容錯控制方法，并通過對航天器跟蹤誤差系統的數字仿真，驗證了本文方法的可行性及魯棒性。該控制器克服了執行器衰退、慣量不確定性及外界干擾對系統穩定性的影響，且具有結構簡單，易于工程實現等優點。