最少錢幣數量的計算與錢幣面額的確定

肖紅德

XIAO Hongde

河南大學 數學與統計學院，河南 開封 475004

School of Mathematics and Statistics,Henan University,Kaifeng,Henan 475004,China

1 概述

計算機作為一種工具，在處理需要大量計算的場合發揮著巨大的作用，在解決需要大量計算的問題上，一般涉及兩方面：一方面是需要設計相關的算法盡量降低算法的復雜度；另一方面在通過計算機語言進行實現的時候還需要對算法進行優化，從而使得在解決問題時盡可能地提高效率。本文通過結合埃拉托色尼篩法、迪杰斯特拉算法和圖的廣度優先遍歷算法的思想，提出了一種用來計算平均錢幣數量的快速算法，即最少錢幣數量篩法，并通過計算給定范圍的三種錢幣組合計算其平均錢幣數量，與動態規劃算法相比，計算速度明顯加快，與貪心算法相比，計算結果更好。對于給定范圍、給定錢幣種類，如何確定錢幣組合這個問題，本文通過對不同錢幣之間數值特征的分析，給出了各個數值滿足的擬合曲線，從而在尋找最佳錢幣種類組合上使得算法的時間復雜度大大降低，程序的運算時間大大縮短。文中選擇MATLAB R2017b作為運行環境，針對上述提出的兩種算法進行了具體實現。

2 相關研究

關于紙幣面值的組合情況研究，Jeffrey已經給出了相關研究結果，見參考文獻[1]。其結果如表1所示。

表2給出的貨幣最佳發行方案是通過動態規劃算法計算出來的。動態規劃有關的算法見參考文獻[2-4]，本文計算的結果與Jeffrey給出的結果不同，原因是Jeffrey計算的范圍包括1但不包括100，且按照100進行平均。如果本文也按照這樣的方法進行計算，則得到的結果與Jeffrey相同。其他錢幣方案中平均錢幣數量的計算與此類似。

對于給定某個值，在計算其所需要最少數量錢幣組合的時候，如果錢幣種類多于兩種，盡管貪心算法計算速度比較快，卻一般不能使用貪心算法進行計算，貪心算法的相關內容見參考文獻[2，5-6]。這是由于對于貪心算法計算出來的結果，在某些組合下不能得到最優結果。比如，使用貪心算法，對于1-5-16-23-33這種組合，在計算32最優組合方案時，使用貪心算法計算的結果是32=23×1+5×1+1×4，一共需要6個錢幣，而如果使用動態規劃計算結果為32=16×2，一共需要2個錢幣。因此，貪心算法在有些情況下得到的不是最優錢幣組合。

對于錢幣種類的確定還有很多其他相關研究，比如參考文獻[7]研究了有關增加某個錢幣面額的數值分析和確定方法。

3 確定平均錢幣數量的快速計算方法——最少錢幣數量篩法

借助埃拉托色尼篩法（見參考文獻[8-10]）、迪杰斯特拉算法（見參考文獻[11-13]）、圖的廣度優先遍歷算法（見參考文獻[11]）的思想，提出一種新的對于給定錢幣種類之后在一定范圍內進行快速計算最少需要錢幣數量的算法，以下稱之為最少錢幣數量篩法。

最少錢幣數量篩法實現的具體計算過程如下：

首先令W為給定數值的錢幣組合，V為一定范圍內的數據集合，cur:=1，cur值用于表示當前能夠計算出來的錢幣值所需要的最少錢幣數量，把需要計算的錢幣范圍V分成兩組：

（1）S，已求出最小錢幣數量的錢幣集合（初始時為0）；

（2）T:=V-S，尚未確定最小錢幣數量的錢幣集合（初始時為V的全集）。

然后進行以下計算過程：

（1）將S中新加入的每一個數加上W中的每一個數（初始時認為新加入的數是0），若得到的數在T中，則將其加入到S中，其錢幣數量記為cur；

（2）修改集合T，去除（1）中S新加入數的集合；

（3）將cur值加1，即cur:=cur+1；

（4）重復執行（1）～（3），直到集合T為空。

4 對任意數量范圍內通過構造錢幣組合確定平均錢幣數量

對于不同錢幣數量最優組合的確定，給定錢幣范圍[1,n]，N種錢幣組合的情況，可以構造(n0/N,n1/N,…,n(N-1)/N)這種按照等比數列規律出現的一組數字，這里用(1,a,…,aN-1)表示，其中a=n1/N，為了表達方便，假設其為整數。對于這樣的構造方案，其好處是在計算其平均錢幣數量時可以使用貪心算法來得到某個數值的錢幣數量，這樣方便統計其平均錢幣數量。

表1 Jeffrey的貨幣最佳發行方案

表2 本文計算出來的貨幣最佳發行方案

由上面的構造組合可以得出以下結論：錢幣組合方案的最佳組合不高于構造組合(1,a,…,aN-1)。對于這樣的構造組合，下面通過計算得到平均錢幣數量。

f(1)=最大錢幣值為1的錢幣數值數量

f(2)=最大錢幣值為a的錢幣數值數量

…

f(N)=最大錢幣值為aN-1的錢幣數值數量

則有：

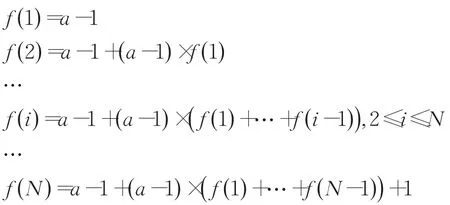
最后+1表示的是aN，即n這一個數的表示。從而有：

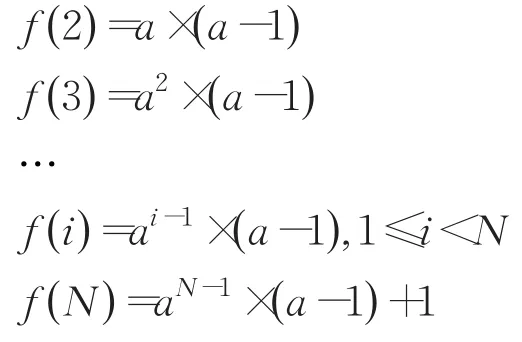
從而可以推出總數量為：

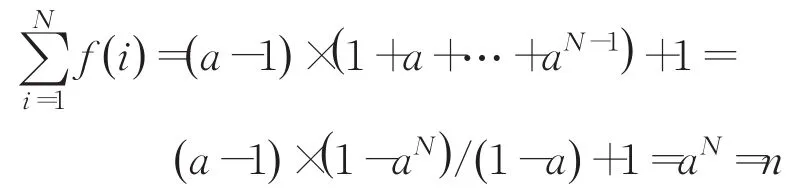
進而說明上述計算的錢幣數值包含錢幣范圍內的所有錢幣數值。

對于通過上述方案構造的錢幣組合，可以計算其平均錢幣數量，具體計算過程如下：令t()

i=由所有最大錢幣面額為ai-1的錢幣組合錢幣數量之和，其中1≤i≤N。則有：

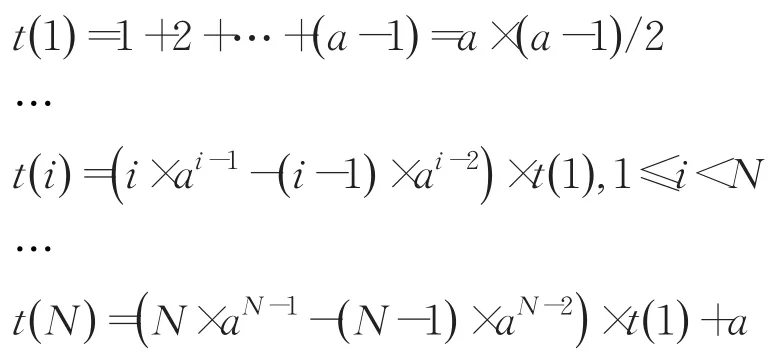
最后+a表示的是aN,即n這一個數的表示，需要的錢幣數量為a。

因此，需要的平均錢幣數量為：

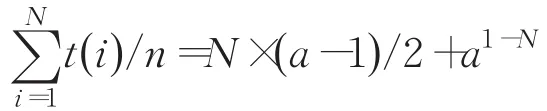
對于三種錢幣的組合，通過遍歷計算得到的平均錢幣數量最優值和上述構造方法得到的平均錢幣數量比值大約在（0.95，1.00）之間，并且隨著范圍的增大，比值也趨向于增大。

5 構造組合和最優組合的對比

對于最優組合的設計，需要將第一個錢幣固定為1，其他錢幣種類需要進行遍歷得到。對于錢幣種類為2的錢幣組合，通過第4章關于平均錢幣數量的計算比較容易得到，第二個錢幣值是關于a0.5的向上取整或向下取整的整數，見表3和圖1。對于錢幣種類大于2的錢幣種類的確定，需要通過遍歷方式得到。

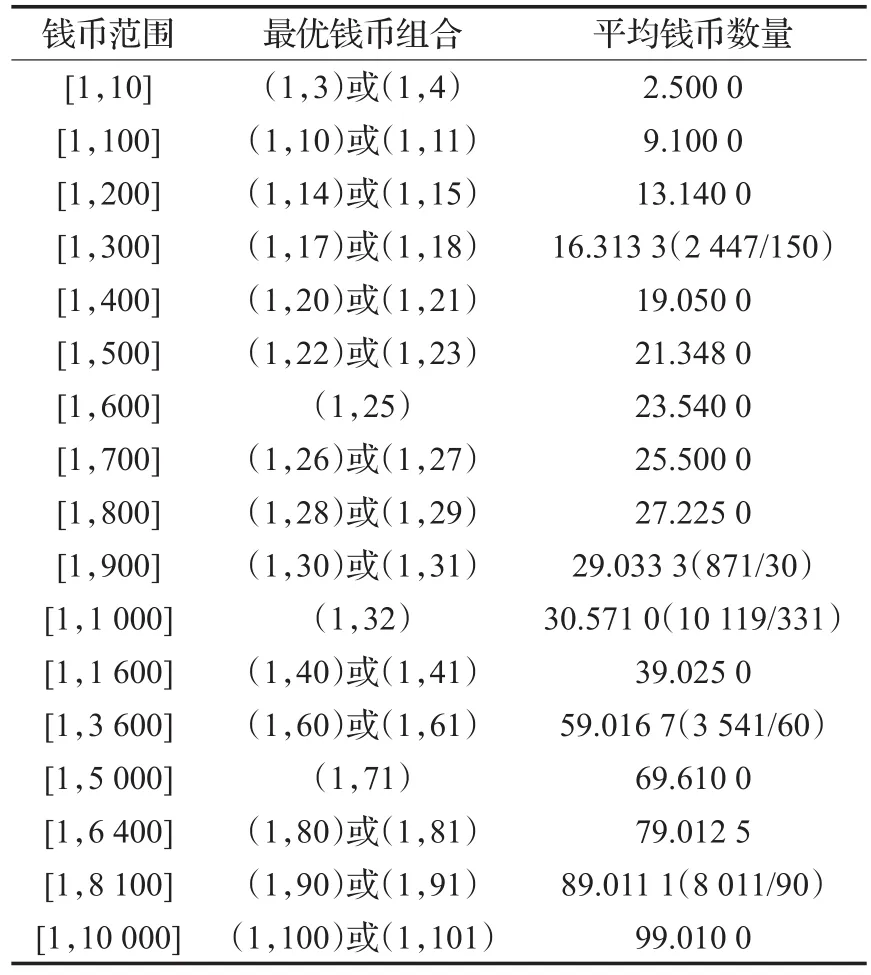
表3 兩種錢幣組合在最優錢幣組合下平均錢幣數量表

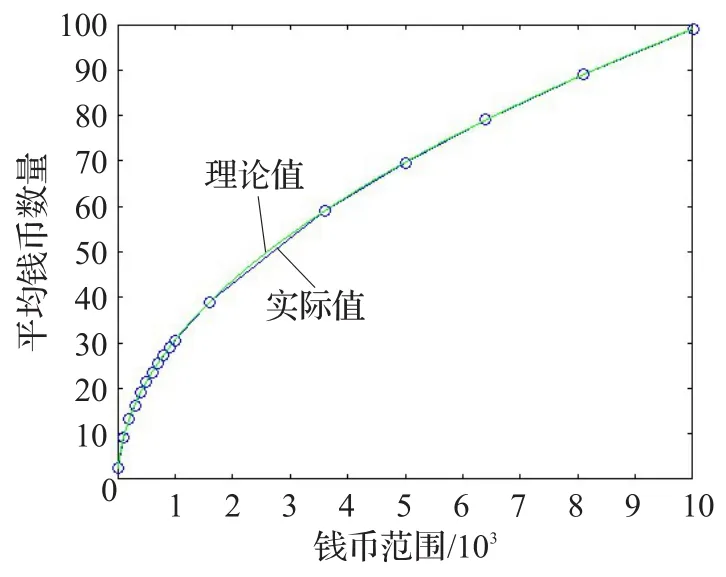
圖1 兩種錢幣組合平均數量理論值與實際值對比

圖1說明：藍線表示在最優錢幣組合下的平均錢幣數量圖，綠色表示通過構造錢幣組合得到的平均錢幣數量理論值，其公式為y=x1/2-1+x-1/2，其中x表示錢幣范圍，y表示平均需要的錢幣數量。通過圖1可以發現，對于兩種錢幣的組合，理論值和實際值基本完全吻合。

以下討論如何確定錢幣的最優組合問題。

對于三種錢幣的最優錢幣種類確定問題，當取值范圍很大時，需要遍歷次數太多，因此需要盡可能縮小遍歷次數。通過計算可知，對于113≤n≤253的情況，第一個數是固定的1，第二個數通過已有例子的模擬（見圖4和圖5）可以確定其曲線擬合表達式為n1040/2711+1255/452，擬合值與真實值的差值在區間[-8197/521,8107/702]上，第三個數的曲線擬合表達式為n25391/38087+1235/478，擬合值與真實值的差值在區間[-8197/521,8107/702]上。第二個數的平方與第三個數的比值處于(2.5,3.2)之間。通過對第二個數和第三個數以及第二個和第三個數之間關系的限定，可以大大減少遍歷次數。

曲線擬合的實現是按照最小二乘法原理進行實現的，有關曲線擬合的MATLAB實現和最小二乘法原理見參考文獻[14-18]。

對于三種錢幣的最優錢幣組合，最終所得結果見表4和圖2。

表4 三種錢幣組合在最優錢幣組合下平均錢幣數量表

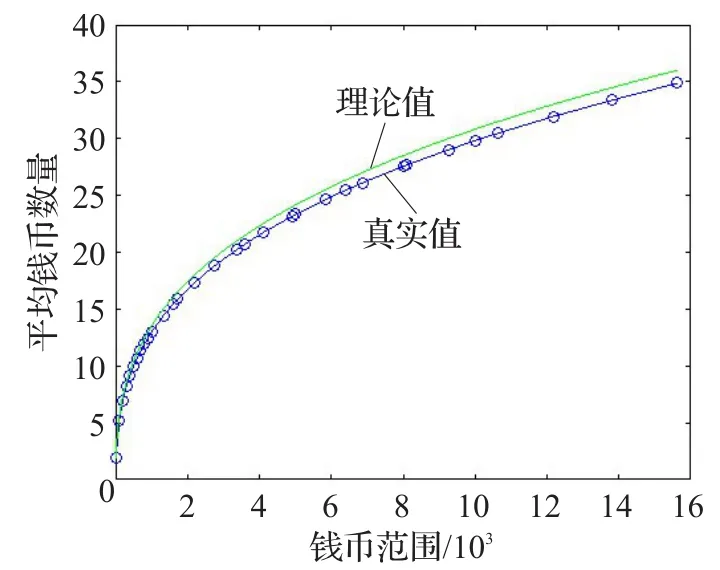
圖2 三種錢幣組合平均數量理論值與實際值對比

圖2說明：藍色表示在最優錢幣組合下的平均錢幣數量圖，綠色表示通過構造錢幣組合得到的平均錢幣數量圖，其公式為y=3×a/2-3/2+a-2，其中a=n1/3。由圖2可知，構造值比真實值要高，真實值與構造值之比主要集中于0.96～0.97之間。

以下是計算3個最優錢幣組合與數值范圍n相互之間關系的模擬效果圖。圖3中橫軸表示數值范圍n，縱軸表示第二個數的平方與第三個數的比值。第二個數和第三個數之間差值的計算可以通過該結果進行估計。

第二個參數和第三個參數之間的關系可以通過圖3的模擬結果進行估計。第二個數的數量級可以通過圖4的模擬結果進行估計。第三個數的數量級可以通過圖5的模擬結果進行估計。

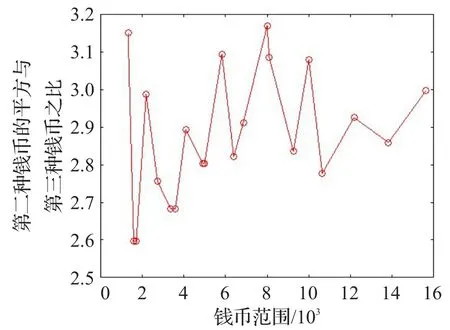
圖3 三種錢幣組合第二個數與第三個數的關系

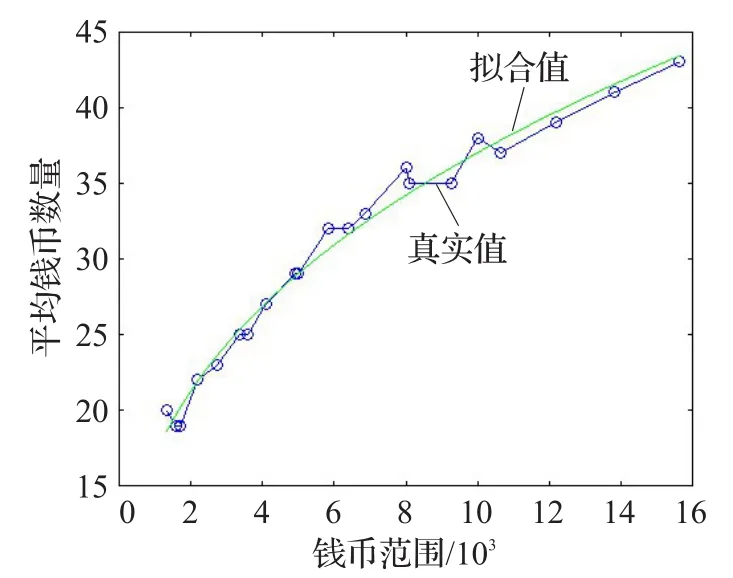
圖4 三種錢幣組合第二個錢幣值的擬合效果圖

圖3說明：在該圖中，最大值為1296/409（約為3.1687），最小值為361/139（約為2.5971）。

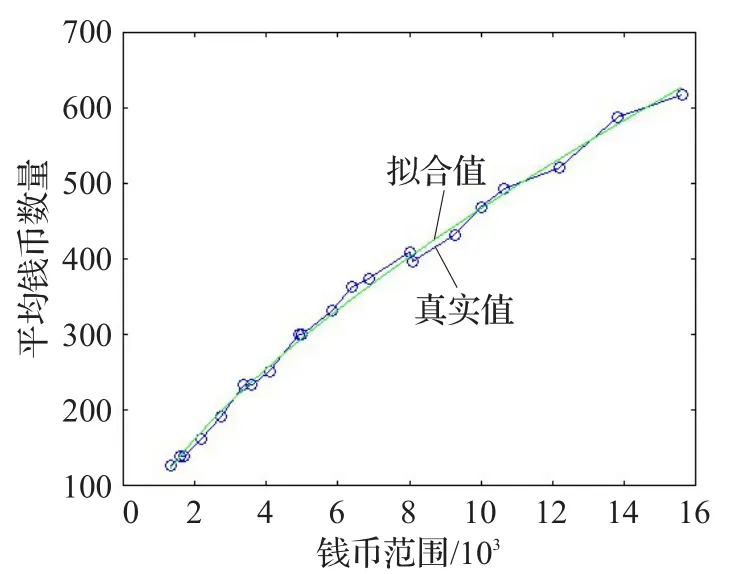
圖5 三種錢幣組合第三個錢幣值的擬合效果圖

圖4說明：藍色曲線表示第二個錢幣種類的真實值，綠色表示第二個錢幣種類的曲線擬合值，其擬合曲線方程為y=x1040/2711+1255/452，其中x表示錢幣的范圍，y表示第二個錢幣種類的曲線擬合值，擬合值和真實值的最大差值為1216/985（約為1.2345），最小差值為-853/475（約為-1.7958）。

圖5說明：藍色曲線表示第三個錢幣種類的真實值，綠色表示第三個錢幣種類的曲線擬合值，其擬合曲線方程為y=x25391/38087+1235/478，其中x表示錢幣的范圍，y表示第三個錢幣種類的曲線擬合值，擬合值和真實值的最大差值為8107/702（約為11.5484），最小差值為-8197/521（約為-15.7332）。

四種以及更多種錢幣組合的確定更為復雜。與三種錢幣組合的確定類似，第一個數是固定的1，后面的數值需要通過遍歷或者通過已經找出的數值發現數值規律，在規律的基礎上進行限制，這里不再討論。

6 結論

本文提出了一種對于給定錢幣組合在給定范圍情況下快速計算需要的平均錢幣數量的方法，對于三種錢幣組合，給出了一種確定錢幣范圍的計算方法，并在此基礎上對錢幣種類的范圍進行了限制，其好處是可以大大減少對于最佳錢幣組合的搜索范圍。