中學物理實驗操作評價研究
邢紅軍 靳 萱
(1. 首都師范大學 北京 100048; 2. 北京匯文中學 北京 100061)
長期以來,如何對中學生的物理實驗操作能力進行有效評定,一直是物理教育界關注的重點課題.由于紙筆測驗難以對中學生的物理實驗操作能力進行有效考查,就在一定程度上妨礙了中學生物理實驗操作能力的發展.有鑒于此,本文對中學生物理實驗操作評價指標展開系統的理論研究,期望能夠給我國中學物理實驗教學的發展以有益的啟示.
1 中學物理實驗操作評價指標的構建
為了準確考察中學生的物理實驗操作能力,需要借助于物理實驗.但如何對實驗操作步驟賦分,就需要有一把作為標準的“尺子”來丈量.而這把“尺子”,就是中學物理實驗操作評價指標.考慮到評價指標的層次性,我們將中學物理實驗操作評價指標的構建分為一級指標和二級指標分別加以建構.
1.1 一級指標的構建
中學物理實驗操作評價的一級指標,應當結合中學物理實驗的特點,遵循簡單、易行、可測量的原則,按照實驗操作的步驟順序,對實驗步驟進行合理取舍,抓住物理實驗的核心要素進行構建.按照這種思路,我們經過系統的理論研究,建構了中學物理實驗操作評價的一級評價指標.如表1所示.
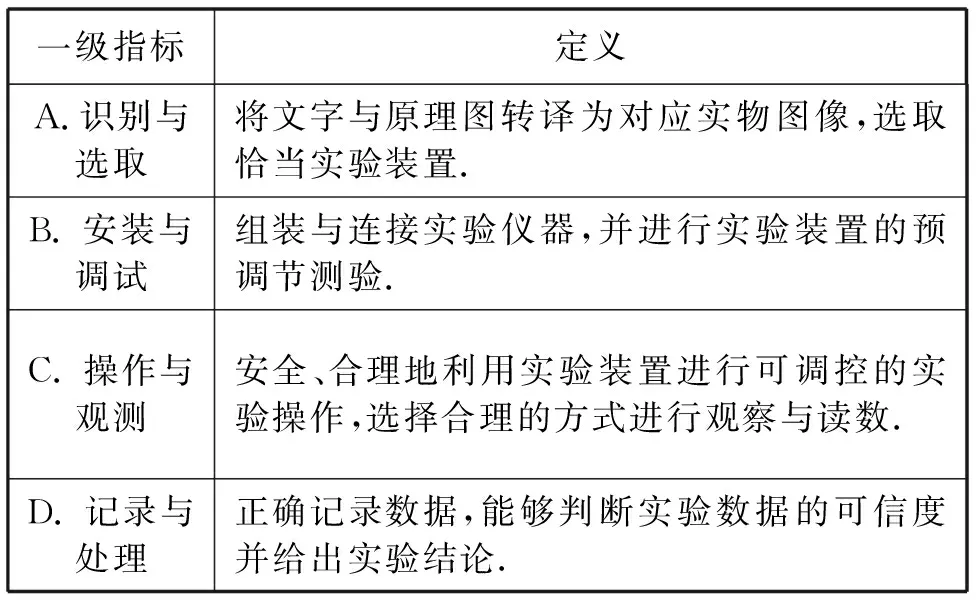
表1 中學物理實驗操作評價的一級評價指標
1.2 二級指標的構建
依據中學物理實驗操作的具體步驟,有必要進一步將各項一級指標進行細化,這就需要建構二級指標.為確保二級指標構建的合理性,我們在研讀物理課程標準的基礎上,分析其所規定的20項必做物理實驗,同時結合已有文獻,確定出二級指標,如表2所示.
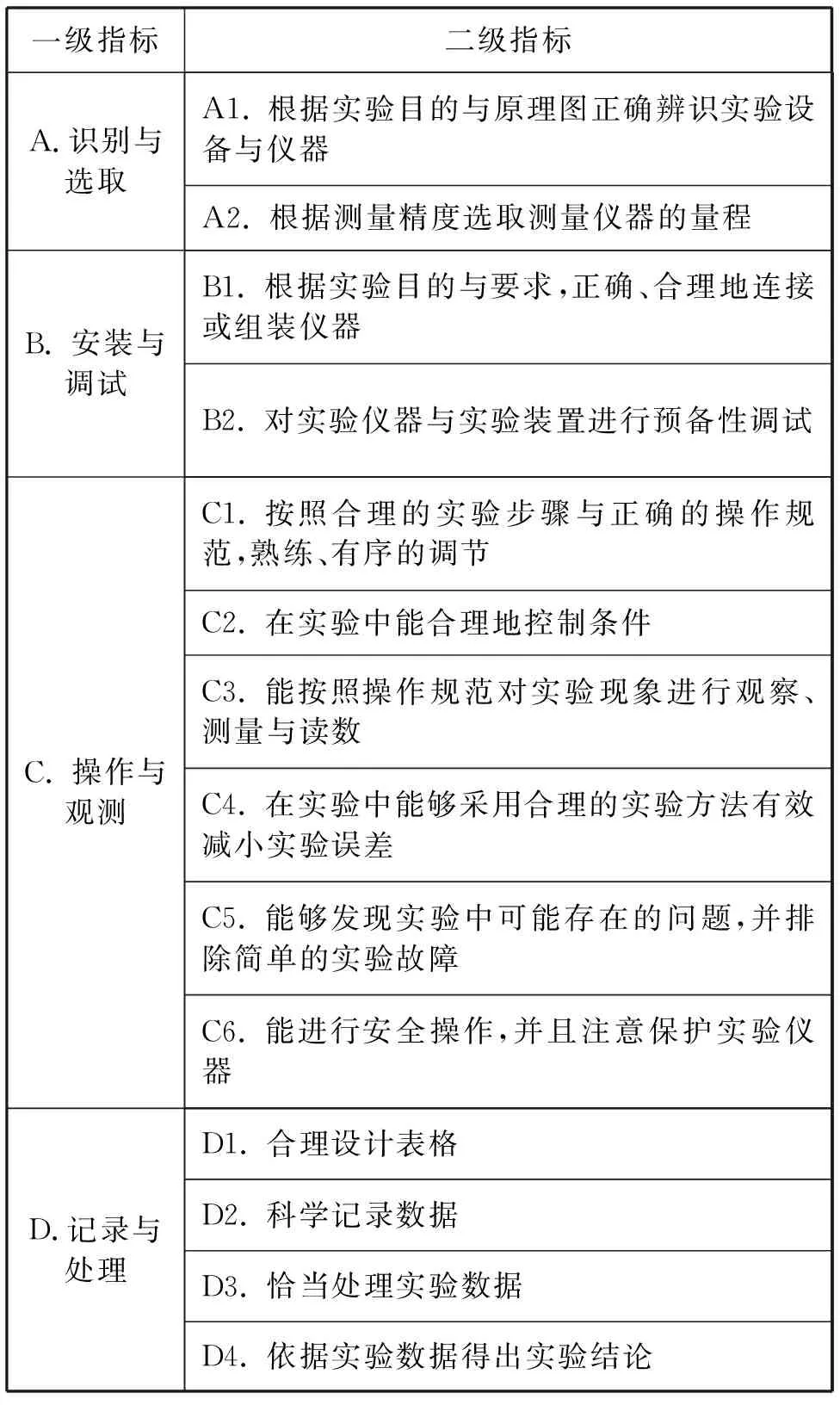
表2 中學物理實驗操作評價的二級評價指標
2 中學物理實驗操作評價指標的信度分析
二級評價指標的建構只是中學物理實驗操作評價指標建構的第一步,接下來,需要對評價指標進行信度分析,從而保證評價指標的信度.
本研究采用問卷調查法確定各項指標的權重.為使被調查者能更準確的對指標按重要性排序,體現指標間重要程度差異.本研究采用李克特十級量表進行測量.調查對象均為教學論專家、一線教師以及物理教學研究人員.問卷共發放139份,回收問卷139份,剔除24份無效問卷,有效問卷總計115份,有效率為83%.
調查問卷的信度分析,是對調查問卷測量結果一致性的分析.信度越高,表明問卷的一致性越強,結果穩定且可靠.因此,為了了解問卷各變量間的一致性與可靠性,故對問卷的同質性信度進行測量.結果如表3.
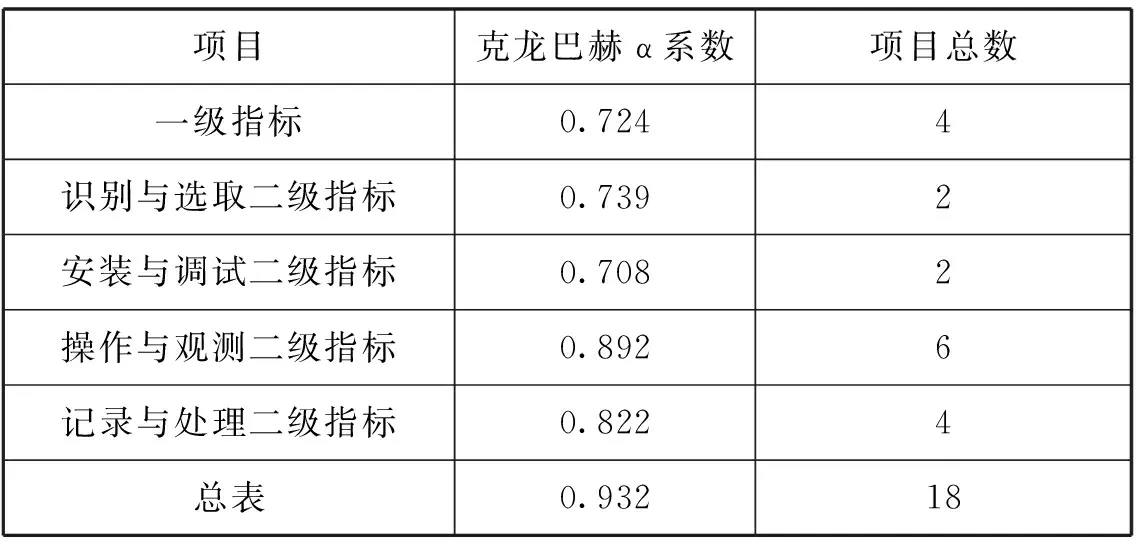
表3 中學物理實驗操作評價指標信度分析
如表3所示,一級指標、識別與選取二級指標、安裝與調試二級指標的克龍巴赫α系數大于0.7.這表明上述指標內在一致性較好,信度良好,測驗結果較為可靠;操作與觀測二級指標、記錄與處理二級指標的克龍巴赫α系數大于0.8.這表明上述指標內在一致性很好,信度很高,測驗結果很可靠;總表的克龍巴赫α系數大于0.9,這表明調查問卷整體內在一致性很好,信度很高,測驗結果非常可靠.
值得注意的是,識別與選取、安裝與調試的二級指標信度相較其他的指標信度較低,我們認為,這是由于該指標中變量數目較少造成的,變量的多少會影響信度的高低.一般情況下,變量數目增多,信度上升,這與克龍巴赫α系數的計算方法有關.本問卷中,上述兩項一級指標分別只對應2個變量,因此信度相對較低.但是,所有指標的克龍巴赫α系數均大于0.7,這表明調查問卷內部一致性較好,可靠性較高.
3 中學物理實驗操作評價指標的效度分析
為了使中學物理實驗操作評價指標在具體測驗中是有效的,需要進一步對評價指標進行效度分析,從而保證評價指標的有效性.
本研究利用SPSS22對問卷的結構效度進行測量.首先對數據進行“KMO和Bartlett球形度檢驗”,獲取KMO值;如果KMO值大于0.5,則可對數據進行因子分析;如果起始特征值大于1.0的變量,其累計解釋變異量占比大于60%,則表明問卷結構效度良好.具體因子分析如表4所示.
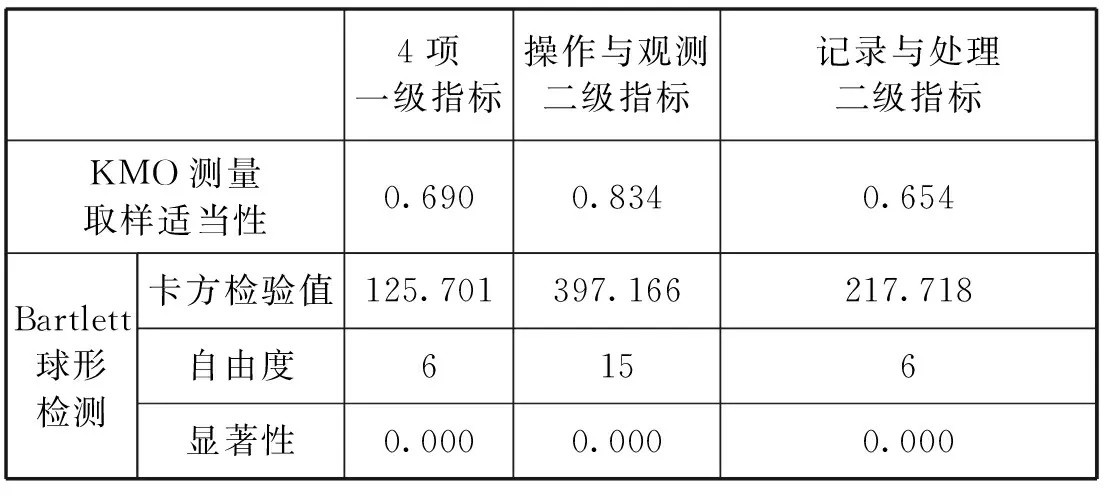
表4 中學物理實驗操作評價指標的KMO值分析
由表4可以發現,3項KMO值均大于0.5,故可以對其進行因子分析,因子分析結果如表5所示.
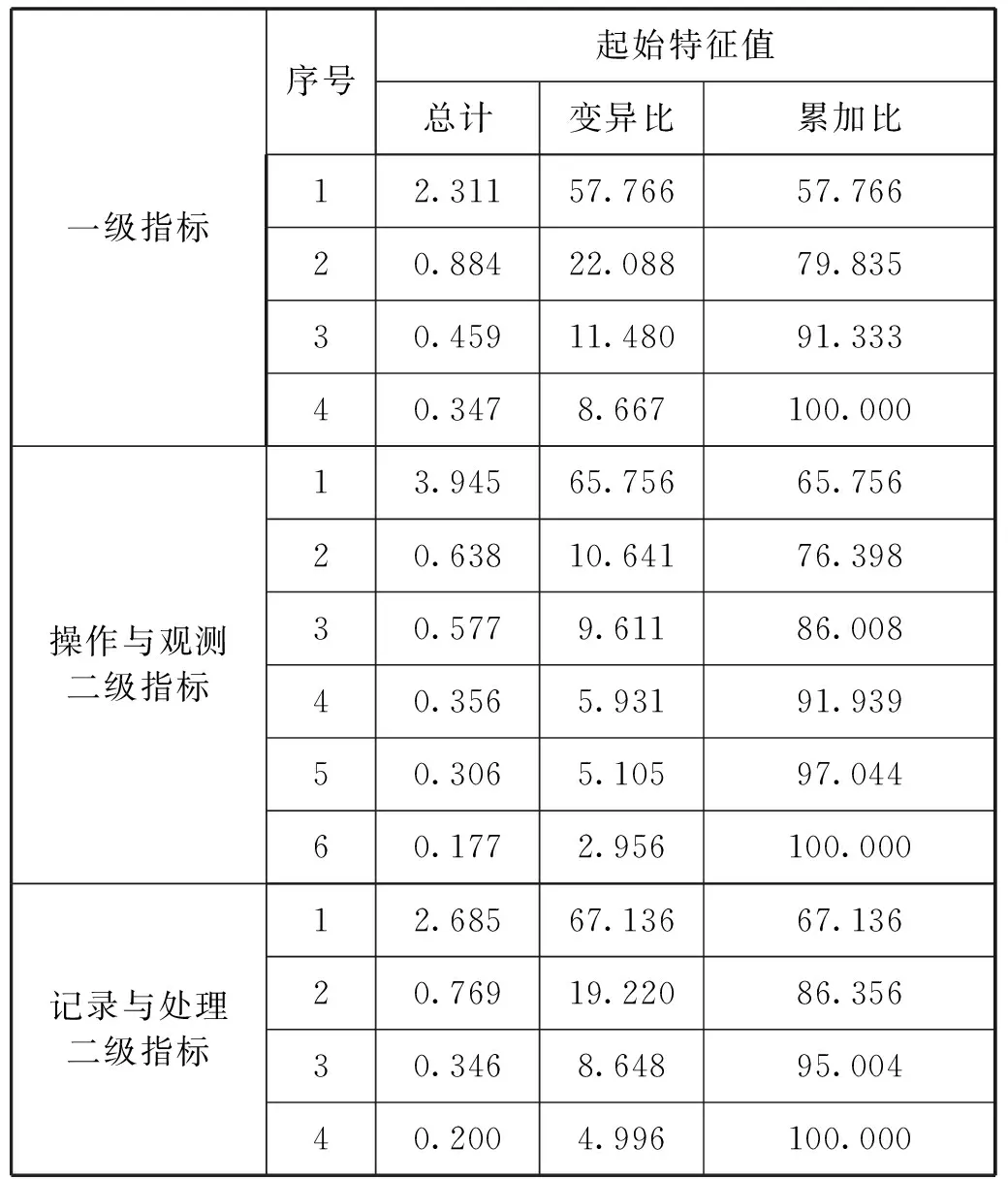
表5 中學物理實驗操作評價指標的因子分析
由表5可知,4項一級指標的累積解釋變異量為57.766%,大于40%,表明該結果是可接受的.其余兩項累計解釋變異量大于60%,表明指標的結構效度良好.
4 中學物理實驗操作評價指標的權重分析
在對中學物理實驗操作評價指標進行信度與效度分析的基礎上,還要對評價指標進行權重分析.這是中學物理實驗操作評價指標能夠應用于實驗測驗的必要步驟.
權重,表明該指標的重要程度.調查問卷的全部指標權重之和為1,每項指標的權重用小數進行表示.我們將采用調查問卷所獲取的數據,借助層次分析法對各項評價指標的權重進行確定.
層次分析法(AHP)是由美國匹茲堡大學教授薩蒂于20世紀70年代初提出,其開創性的把定性與定量的研究方法聯系在一起,常用于多目標的決策.該方法的特點為,可以以少量的定量信息為基礎,將決策過程數學化,為解決多目標、多準則的繁復問題,給出一套系統、簡潔,且高效的決策范式.在使用層次分析法時,需先將待處理的復雜問題拆分為若干層次與因素,并對不同層次與因素進行重要程度的兩兩比較,之后建立判斷矩陣,最后利用判斷矩陣的最大特征值與特征向量,得出指標權重.
首先,為了確定兩個不同因素的重要性程度,現對標度的選取進行規定,如表6所示.
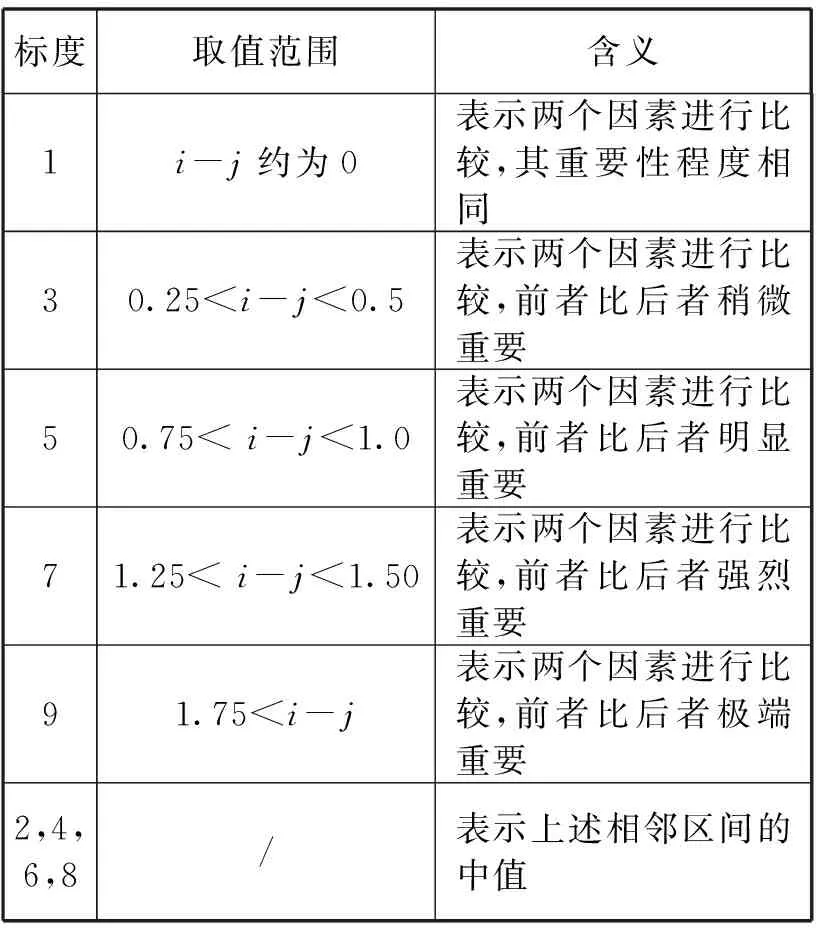
表6 標度選取的規定
現以4項一級指標的權重計算為例,介紹權重的計算過程.
(1) 確定各指標的平均值.
根據調查問卷的測量結果,一級指標的平均得分如表7所示.
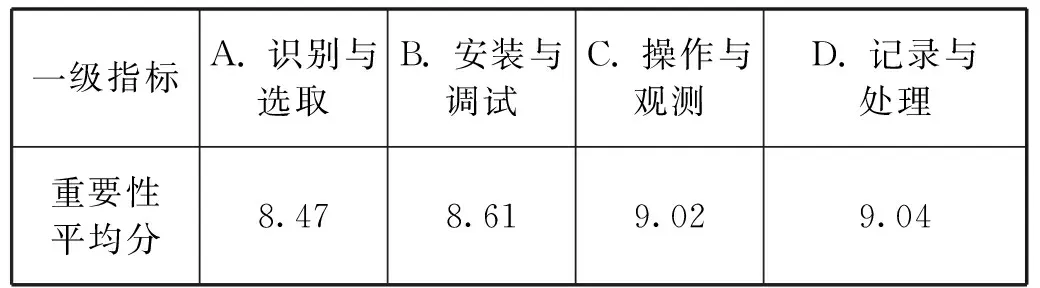
表7 各項一級指標的重要性程度平均得分
(2) 確定判斷矩陣.
由表7可以發現,D的重要性程度平均得分最高,值為9.04.現用D的分數與A的分數做差得0.57,介于0.5與0.75之間,故標度取值為4,意為“D相較A明顯重要”.根據上述方法,依次判斷出D與B、C的標度,填入判斷矩陣當中.一級指標的判斷矩陣A如下所示:
(3) 計算各個元素的權重.
① 對上式利用算術平均法進行權重的計算,得到最終的權重向量W(亦稱為最大特征值對應的特征向量):

(4) 檢驗判斷矩陣的一致性.
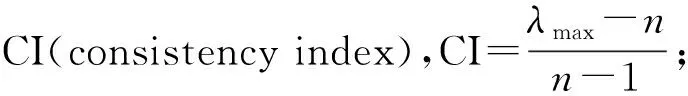

表8 一致性指標RI數值
如果數據的一致性比例系數CR<0.10,則認為判斷矩陣的一致性較好,結果
能夠被接受.
③ 用判斷矩陣A乘以權重向量W,再根據AW=λmaxW求出最大特征值λmax,因此CI=0.007.由于判斷矩陣A為4階矩陣,查表可知RI=0.89,則CR=0.01.由于CR<0.1,故判斷矩陣A一致性很好.
根據上述計算方式,最終得出中學物理實驗操作評價各項指標的分值分配,如表9所示.
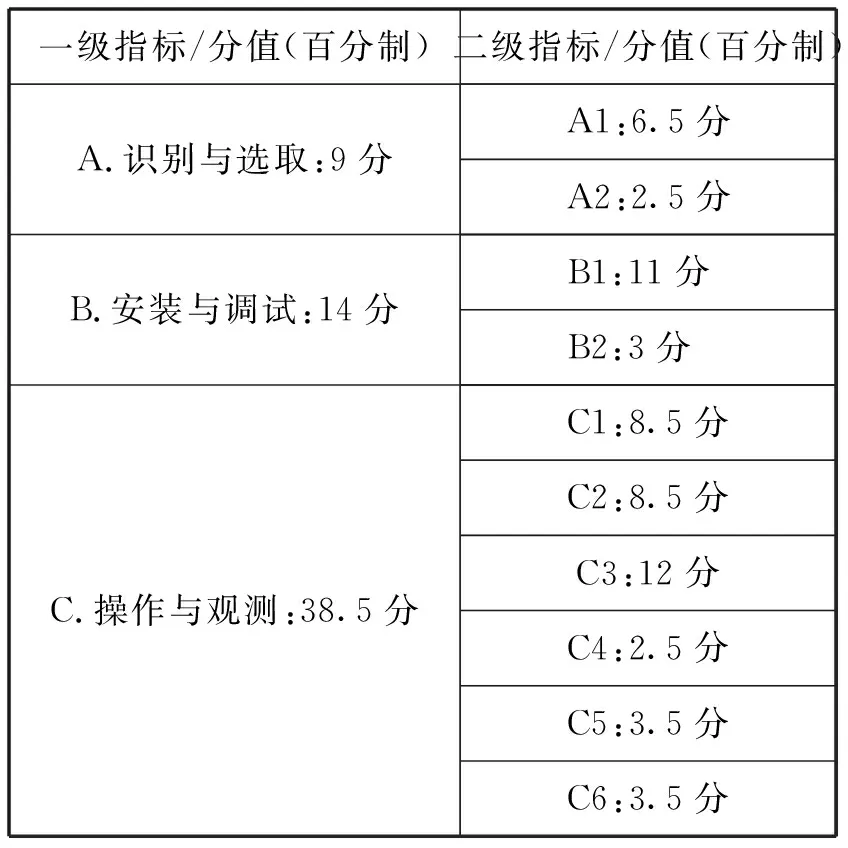
表9 中學物理實驗操作評價各項指標的分值
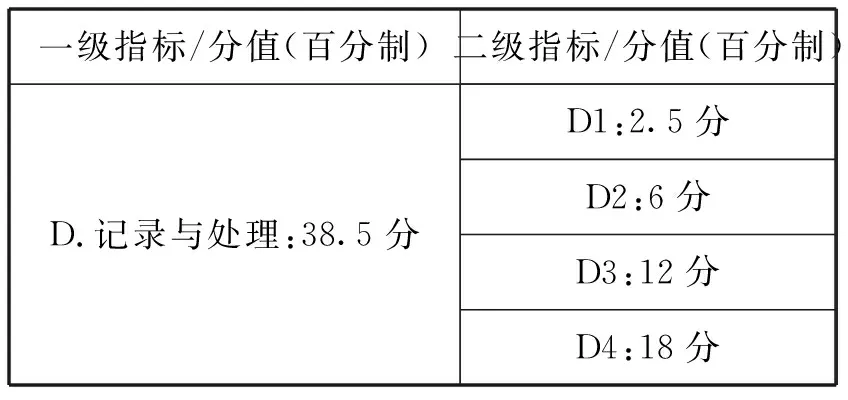
續表
至此,中學物理實驗操作評價指標的理論建構完畢.評價指標經過信度、效度檢驗與權重確定后,就成為一個標準的中學物理實驗操作評價指標,可以用來指導中學物理實驗操作的評價.顯然,這樣一個標準化的中學物理實驗操作評價指標,就具有重要的理論價值與實踐價值.

