基于嵌入分數維的樹種算法的結構質量剛度識別

趙一霖, 劉濟科, 丁政豪, 呂中榮

(中山大學 工學院， 廣州 510006)

結構損傷識別一直是許多學者關注的重點問題，對于結構行之有效的檢測可以避免很多事故的發生[1]。在相關研究中，許多學者將結構損傷模型等價為單元剛度矩陣中楊氏模量的減少[2]，質量的改變[3]，以及一種完全開口裂紋的模型[4]等等。但是將單元的損傷同時歸結為質量和剛度同時改變的研究較少。另一方面，在損傷程度反演的研究中往往把該問題歸結為優化問題[6-11]，即通過定義一個關于損傷結構的目標函數，然后利用各種優化方法來實現結構參數的損傷檢測。而利用經典的優化方法往往需要好的初始值，借助梯度和導數等信息,所以極大地限制了這些方法的應用。在這一方面，群智能算法則可以彌補經典優化方法的不足。在這一族方法中，樹種算法因為方便執行，尋優能力較傳統算法如GA (Genetic Algorithm)，PSO (Particle Swarm Optimization)等算法更強[12],進而引起了注意。本文旨在利用嵌入分數維機制的樹種算法來實現結構的質量剛度識別。首先引入樹的搜索階段。第二步在標準樹種算法上，引入了兩種更好的搜索模式，進而使得算法的局部搜索能力和全局搜索能力得以平衡。基于損傷結構的加速度響應建立損傷識別問題的目標函數,利用改進后的算法對該目標函數進行求解以獲得損傷參數的識別。

1 目標函數

在本文中，將結構的損傷歸結為單元剛度和質量的同時減少，所以可以利用一系列折損系數αi(i=1,2,…,n)，βi(i=1,2,…,n)來描述。αi=βi=0時表示結構無損，αi=βi=1時則表示結構完全破壞。損傷結構的整體剛度和質量矩陣又可以表示為

(1)

(2)

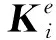
(3)

2 改進的樹種算法

樹種算法是一種新型的群智能算法。它主要是模仿大樹的繁衍方式來對最優解進行尋找。對于每一棵樹(可行解)首先會隨機地產生若干種子，每一顆種子根據趨勢函數ST (Search Tendency)來選擇適合自己的搜索模式。然后對原解和若干種子產生的可行解進行評估，選擇留下適應度更好的解。所以與一般的群智能算法相比(如人工蜂群算法(Artificial Bee Colony， ABC)和螢火蟲算法[13])該算法的局部搜索模式更為劇烈和精細，所以具備了更好的全局尋優能力。關于樹種算法的詳細描述可以參考丁政豪等的研究,以下重點介紹樹種算法的改進部分，即MTSA (Modified Tree Seed Algorithm)。

2.1 嵌入分數維的初次尋找

參考人工蜂群算法的雇傭蜂搜索，所以擬在標準TSA算法中引入一個‘樹的搜索’即對初始種群進行一個大致地尋找，然后在進行樹種搜索。在這個階段里面，搜索的初期(迭代剛開始的階段)，為了保證種群的多樣性，采用如下搜索模式

Ti,j(iter+1)=Ti,j(iter)+γi,j×(Ti,j(iter)-

Tr,j(iter))

(4)

式中：iter為當前的迭代步數；Ti,j為第ith棵樹的第jth維變量γi,j是分布于[-1,1]的隨機數；Tr,j為種群里面隨機選擇的第rth棵樹，在經過若干次迭代之后，到了迭代后期，則采用嵌入了分數維模型的公式進行后期搜索。分數維的定義如下所示

(5)

式中：Dδ[x(t)]為對函數x(t)求δ階導數；Γ(·)為伽馬函數。在本文中，考慮這種模型的前4階的表達式，由式(5)離散得到迭代后期的搜索模式，如式(6)所示

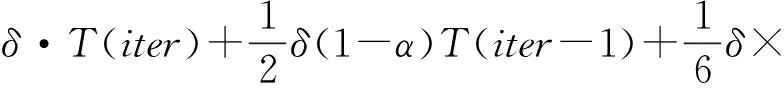
(2-δ)(3-δ)T(iter-3)+φ1(b-x)+

φ2(g-x)

(6)

式中：φ1(b-x)+φ2(g-x)為離散化的時候產生的截斷誤差。在經過前期搜索之后，該公式用來執行后期的搜索。采用分數維模型是因為這種機制具有記憶功能，可以發現在這個表達式里頭每一次迭代都是由之前3次迭代的信息共同決定的，所以在迭代后期，由于同化效應的影響，算法的收斂速度可以得到改善。

2.2 搜索模式的改進

在標準算法中，樹種的全局搜索模式采用了人工蜂群算法中引領蜂的迭代方式

Si,j=Ti,j+γi,j×(Ti,j-Tr,j)

(7)

式中：Si,j為第ith樹繁殖地第ith種子中第jth變量的變異結果；Tr,j為種群中的另一棵樹的第jth變量；γi,j為一個位于[-1,1]之間的隨機數。由于這種搜索模式側重于算法的全局搜索，所以應該采用更加劇烈的方式來描述，站在這點來看，利用差分進化算法中的DE/rand/2/bin變異機制對待優化變量的每一維變量進行變異更為合理，而且文獻[14]已經明確指出了差分進化機制相較于其他引領蜂搜索機制而言有更強的全局尋優能力，所以擬用式(8)來產生新解

Si,j=Ti1,j+F1·(Ti2,j-Ti3,j)+F2·(Ti4,j-Ti5,j)

(8)

式中：Ti1,Ti2,Ti3,Ti4,Ti5為種群中任意5棵不同的數；j為待優化變量中的任意一維變量)，與原始算法的一維攝動產生新解相比，這種方式可以使得變異更劇烈，更加充分地利用種群的信息，從而使得初始狀態的搜索著眼于全局搜索，進而能夠避免“早熟”。其中F1,F2為縮放因子，一般兩者都取0.5。

2.3 局部尋優能力的改善

在原始算法中，樹種的局部搜索方式是圍繞著此次迭代中最好的那一棵樹進行鄰域二次探索來實現的，具體表達式如式(9)所示

Si,j=Ti,j+γ×(Bj-Tr,j)

(9)

式中：Bj為最好的那棵樹的第jth變量；γ為位于[-1,1]之間的隨機數。如果圍繞著最好的可行解周邊進行二次探索是非常有利于算法收斂的。為了更好地實現這個目的，改進算法中擬采用以下方式探索

Si,j=Ti,j+γi,j(Ti,j-Tk,j)+χi,j(Bj-Ti,j)

(10)

式中：γi,j為位于[-1,1]之間的隨機數；χi,j為位于[0,1.5]之間的隨機數。此種模式的尋優不僅利用了最優解的信息而且利用了種群中其它可行解的信息[15]，通過兩個不同范圍的縮放因子可以兼顧收斂速度和全局尋優能力。

3 數值模擬

為了測試算法的有效性，采用了一26桿桁架橋來作為第一個數值算例。它的幾何外形如圖1所示，它的楊氏模量為E=2.1×1011Pa,密度ρ=2.7×103kg/m3, 橫截面積為A=10-4m2。 直桿的長度為L=1 m沖擊荷載選擇為6號自由度(4號節點垂直方向)作用一F=200 N的沖擊荷載；采樣總時長為0.5 s；無損結構的前3階固有頻率分別為77.71 Hz, 147.57 Hz和257.46 Hz。

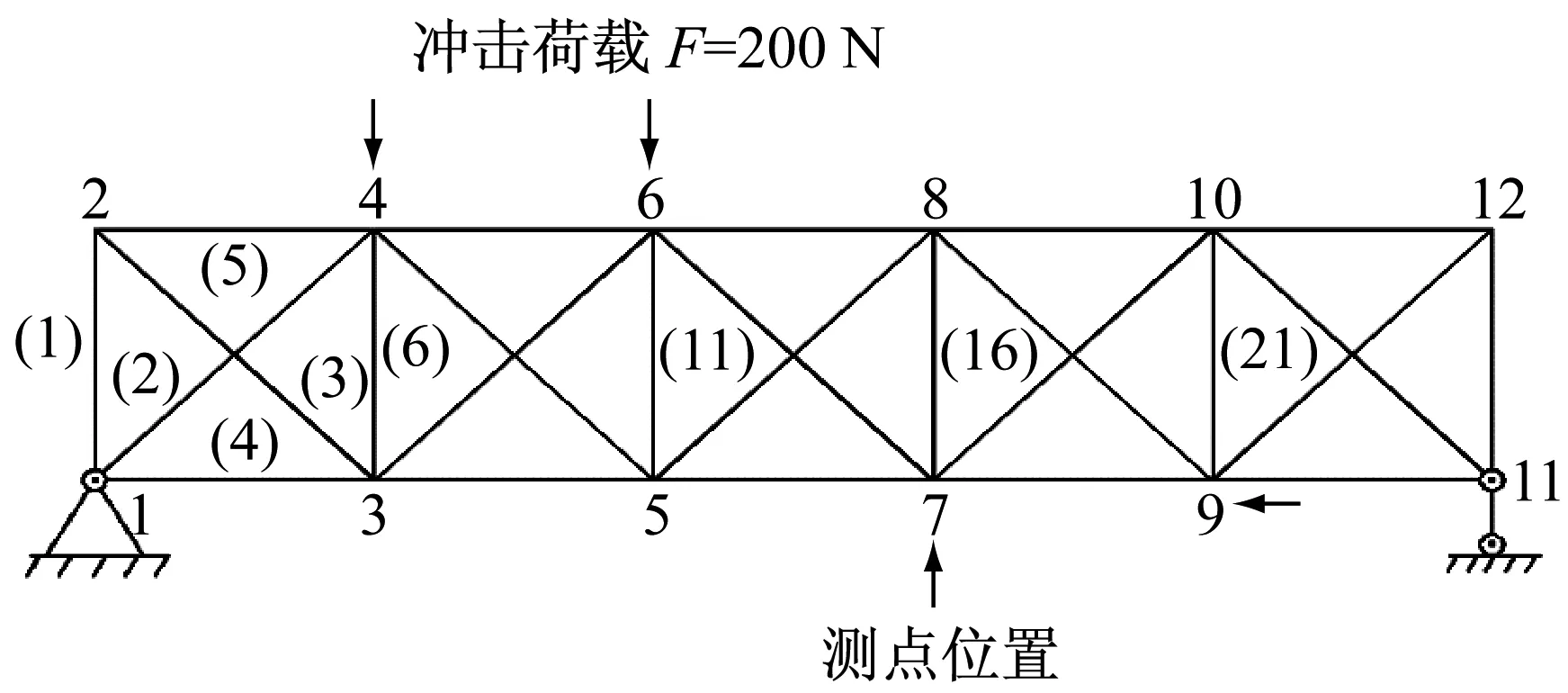
圖1 桁架模型

3.1 損傷工況1

假定6號單元損傷15%的楊氏模量，11號單元損傷10%的質量參數。采用New-mark直接積分法得到某些自由度(10 th，12 th 和15 th)的加速度響應(如圖2所示)，將這些相應數據作為輸入，并且采用遺傳算法(GA)進行比較。算法參數設置如下：初始種群數量為50，最大迭代次數設置為500次；對于遺傳算法，交叉率為0.9，變異率為0.1；每種算法計算10次，統計平均值

和標準差。圖3展示了基于三種算法得到的目標函數進化曲線，可以明顯地觀察到基于MTSA算法得到的曲線是更接近于0的，這就意味著基于該方法得到的識別結果是最好的。相較之下，其他算法如GA由于陷入了局部最優，所以目標函數值在經過200次迭代之后始終維持在102量級,故而完全失效了。更進一步，圖4和表1記錄了最終的識別結果，可以清楚地發現TSA得到的最大誤差為3.811%，而基于MTSA得到的最大誤差僅為0.077%，這充分表明了MTSA在處理該問題上的優越性。

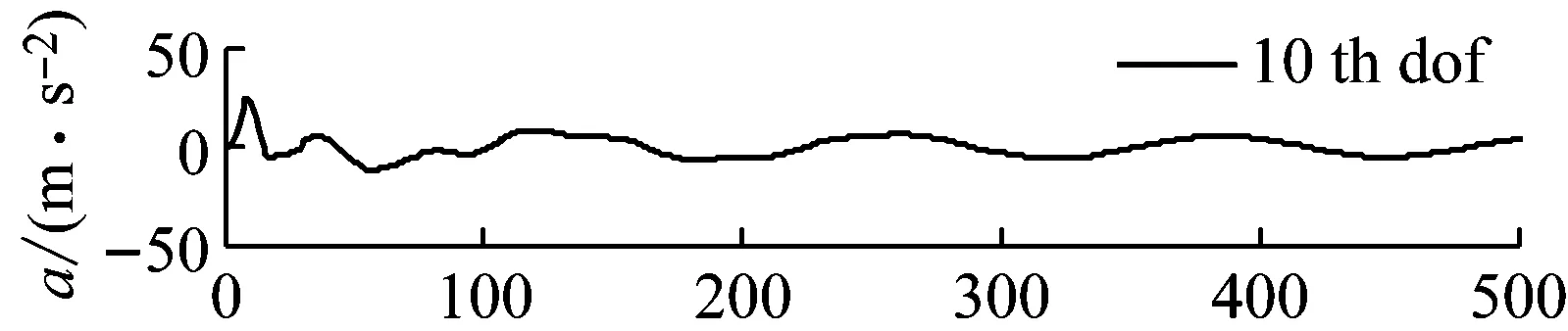
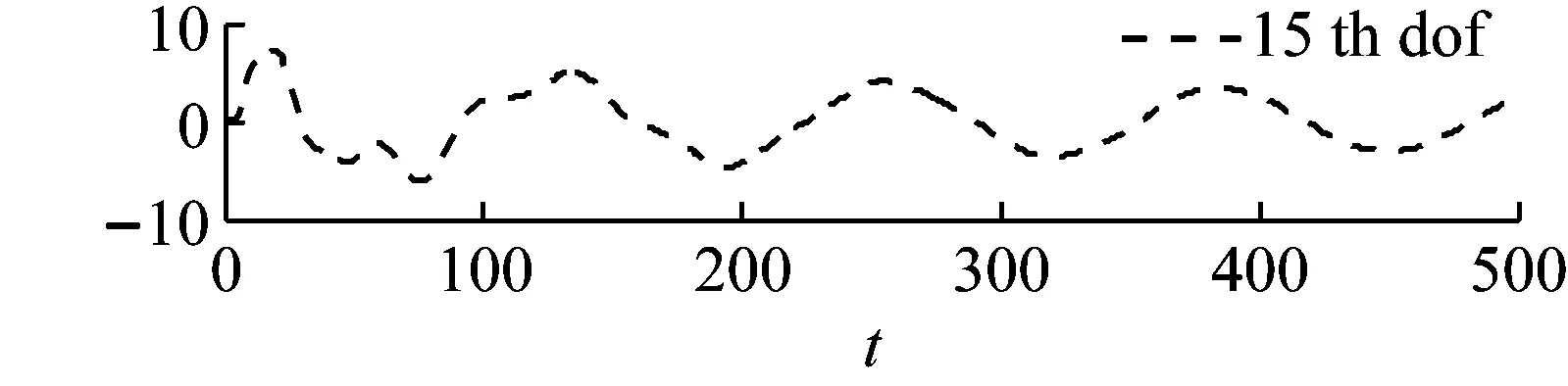
圖2 工況1測點加速度響應曲線

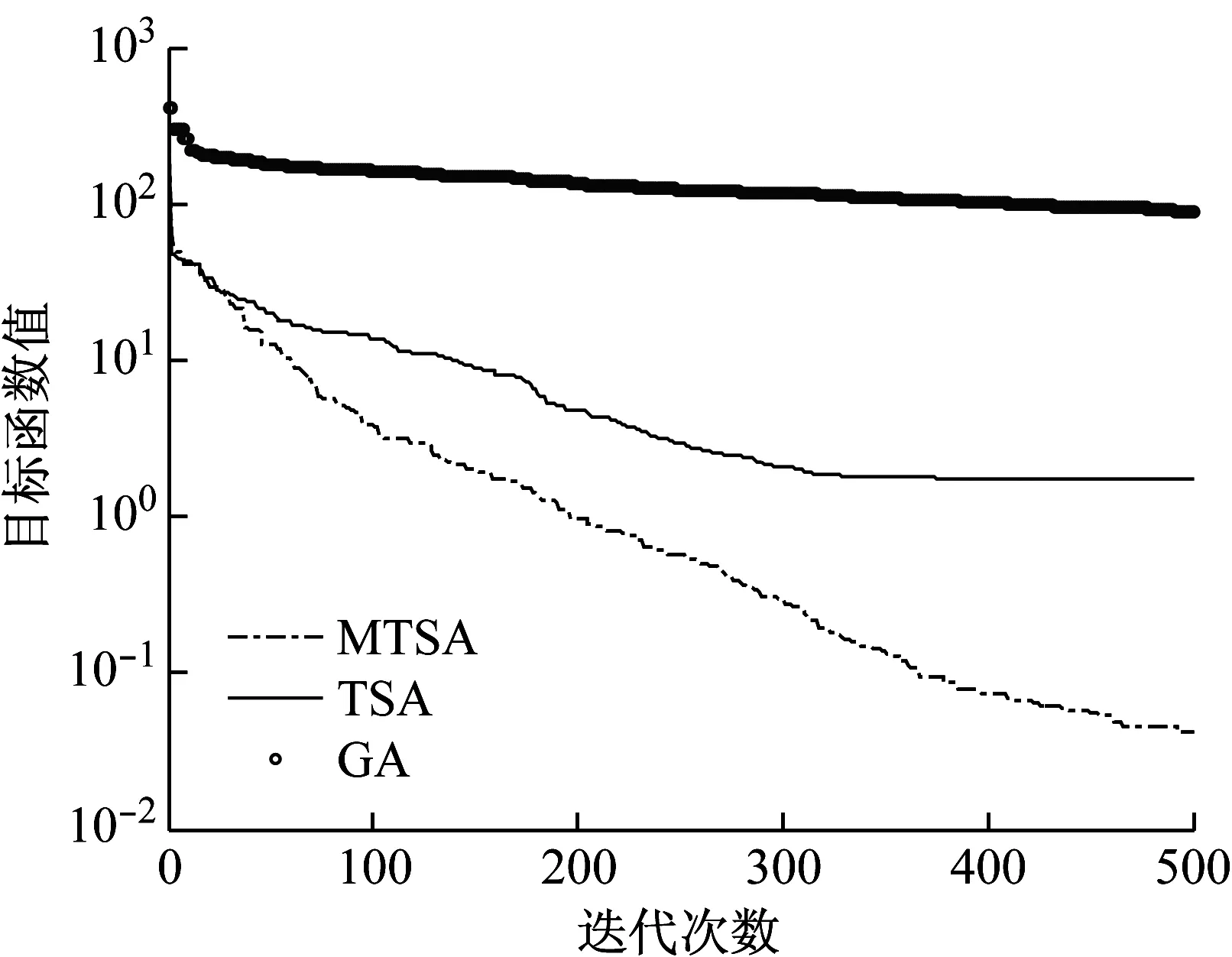
圖3 基于各算法得到的目標函數迭代曲線

圖4 工況1的識別結果

Fig.4 Identified result of case 1

3.2 損傷工況2

第二種情況考慮多點損傷，即假定6號，11號和16號單元存在5%楊氏模量的折損，11號單元存在10%的質量折損，因為GA算法在算例1中已經失效，所以此情況下只有TSA和MTSA算法用來計算結構損傷。為了測試噪聲[16-17]對算法的影響，10%的白噪聲加入到了加速度響應數據。圖5展示了基于改進算法得到的折損因子的迭代曲線，經過100次左右的迭代，算法收斂到了預設值附近。圖6和表1展示了最終的識別結果，可以清楚地發現，即便是運用被污染的響應數據，MTSA對于剛度參數，得到的最大識別誤差為1.76%；對于質量參數得到的誤差也僅為1.065%；同時就標準差而言，MTSA得到的值也是最小的，這充分說明了算法的穩定性和穩健性。

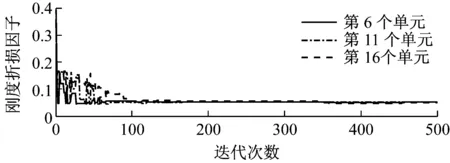
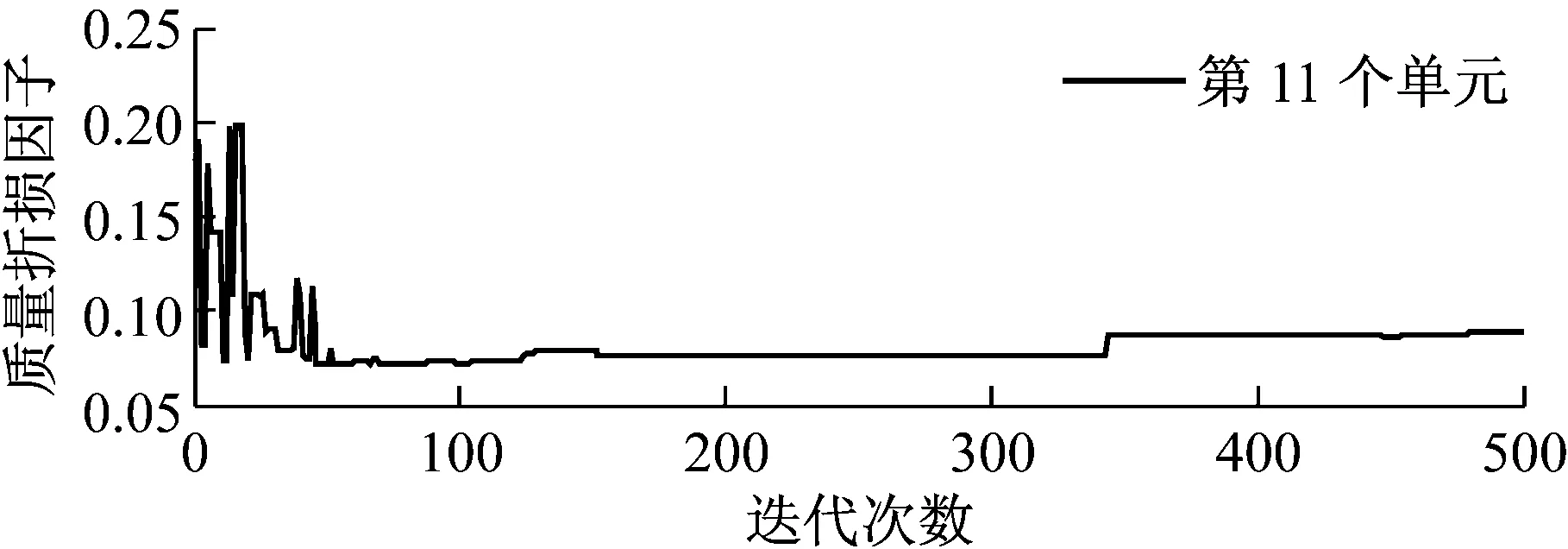
圖5 基于改進TSA得到的折損因子的迭代曲線(工況2)

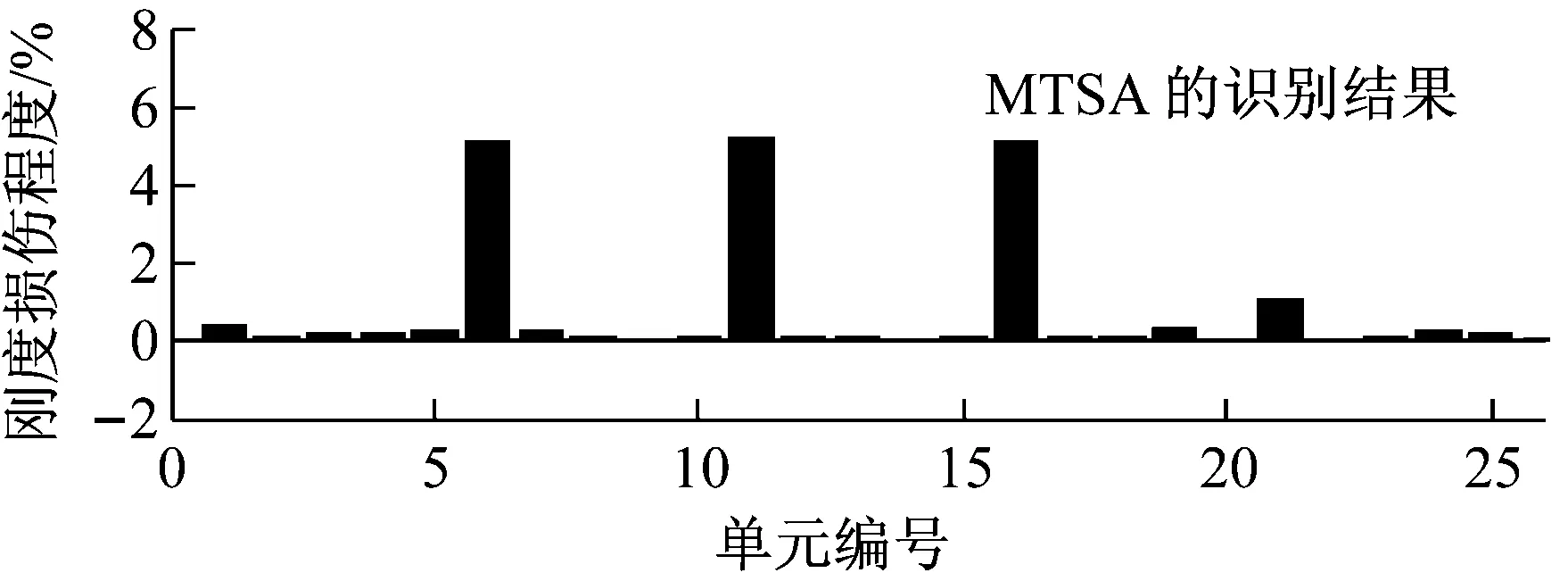
圖6 工況2的識別結果

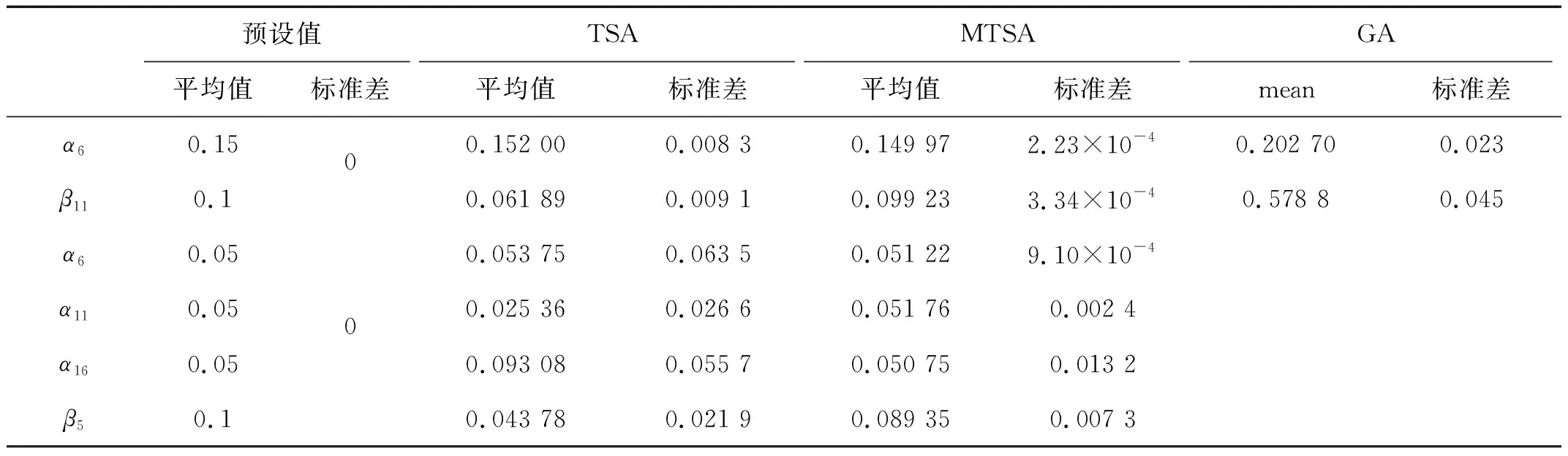
表1 桁架結構的識別結果

4 結 論

本文采用分數維機制改進樹種算法，并且引入了兩個全新的迭代方式，進而使得算法的全局尋優能力和局部尋優能力得以平衡。在損傷模型方面，將結構的損傷歸結為質量和剛度的同時變化。采用加速度響應作為目標函數，以一個26單元的桁架結構作為數值算例，最終結果表明MTSA在響應數據被高等級噪聲污染的情況下，仍然可以得到較好的識別結果。