基于因子圖的狀態估計方法
劉虎成,程詠梅
(1.中國電子科技集團公司第二十研究所,陜西 西安 710129;2.西北工業大學,陜西 西安 710129)
0 引 言
狀態估計也稱過程估計,是指動態系統依據狀態方程和量測方程,由量測數據來估計系統的狀態[1-2]。在動態系統中,一般用狀態方程描述系統狀態隨著時間推移的變化過程,用量測方程描述某種測量方式或傳感器對狀態的觀測。
當前的動態系統主要采用卡爾曼濾波器進行狀態估計,存在的問題有:
(1) 卡爾曼濾波要求系統的狀態方程和量測方程都是線性的,或者在非線性程度不高時使用擴展卡爾曼濾波(EKF),但不適用于非線性程度較高的場景。
(2) 只對當前時刻的狀態進行估計,建立的量測方程只能描述量測與當前狀態的映射關系。當量測數據存在延遲時無法直接使用,需要使用特定的配準方法進行數據對準,會造成精度損失。
(3) 當濾波器內只存在當前時刻的狀態,當歷史時刻狀態與當前狀態存在約束關系時,濾波器不能利用這種約束對當前狀態進行修正。
上述問題限制了卡爾曼濾波在一些特定場景(如同步定位與地圖創建(SLAM)、多狀態約束和量測數據存在亂序延時等情形)下的使用。2006年起,美國喬治亞理工學院的Frank Dellaert和麻省理工學院的Michael Kaess等人使用一種圖形模型(因子圖)對自主移動機器人的SLAM問題[3-5]進行表示和分析,建立了基于因子圖的狀態估計方法。該方法可以在非線性模型下進行機器人軌跡狀態的同時濾波與平滑。同時,基于因子圖的狀態估計方法可以處理多狀態相關量測信息(即量測信息的獲取與多個時刻的狀態相關)。
綜上所述,本文基于美國喬治亞理工學院的研究框架,系統闡述基于因子圖狀態估計方法的基本原理,包括因子圖模型理論與數學意義、狀態估計問題的因子圖模型描述和狀態求解方法。
1 因子圖模型
因子圖這一概念最初在20世紀90年代由F.R.Kschischang等[6-7]在用于分析信道編碼的Tanner圖[8]、Wiberg圖[9]等模型的基礎上推廣而來,其后便成為研究信道估計、解碼及迭代接收機技術的一個通用工具[10-11]。因子圖模型的表示簡潔,概念清晰,用于表示估計問題中的聯合概率密度函數,能夠將狀態與狀態、狀態與量測過程之間的關系可視化。
定義:用集合G=(X,F,E)表示因子圖模型,它包含有2種節點:變量節點X={X1,X2,…,Xn}、因子節點(也稱函數節點)F={f1,f2,…,fm}以及連接2種節點的無向邊E。因子節點fj和變量節點Xk之間存在邊的充要條件是Xk∈Sj存在,邊線E表示因子節點和變量節點間的函數關系[12]。下面用個例子簡要介紹下因子圖的概念及數學意義。
假設有一全局函數g(X1,X2,…,Xn),現在將該函數因式分解為m個因式:
(1)
式中:Sj?{X1,X2,…,Xn},是X的第j個變量子空間;f是一個實值函數,如式:
g(x1,x2,x3,x4,x5)=
fA(x1)fB(x2)fC(x1,x2,x3)fD(x3,x4)fE(x3,x5)
(2)
根據因子圖的規則,式(2)對應的因子圖模型如圖1所示。圖中用圓圈表示變量節點X={x1,x2,x3,x4,x5};用實心黑點表示因子節點F={fA,fB,fC,fD,fE},即全局函數g(x1,x2,x3,x4,x5)的因式,稱為局部函數。從圖中可以看出,因子圖中每一個變量節點對應一個變量,每一個因子節點對應一個局部函數,當且僅當變量是局部函數的自變量時,相應的變量節點和函數節點之間存在一條連接邊。
綜上可知,因子圖模型顯式地表示了多元函數

圖1 公式(2)所對應的因子圖模型
的因式分解。使用因子圖模型處理一個具有多個變量的全局函數時,可將一個復雜的全局函數分解為若干個簡單的局部函數的乘積,進而通過這種分治策略,減小求解全局函數的復雜度。
2 狀態估計的因子圖模型表示
一般來說,對一個動態系統進行狀態估計時,首先要建立狀態方程和量測方程。狀態方程可表示為:
xk=fk(xk-1,uk)+ωk
(3)
式中:xk(k=1,2,…)為tk時刻的系統狀態;uk為驅動狀態動態變化的控制輸入;fk(xk-1,uk)為系統動態轉移模型;ωk為模型誤差噪聲。
量測方程表示為:
zk=hk(xk)+μk
(4)
式中:zk為量測輸出;hk(xk)為量測模型;μk為量測噪聲。

(5)
此時,真實狀態xk和理想量測zk的條件概率分布滿足:
(6)

假定系統直到tk時刻的狀態集合為Xk,量測集合為Zk,則有:
(7)
則直到tk時刻,系統的聯合概率密度函數(JPDF)表示為:
(8)

對于狀態估計問題,在已知系統狀態的JPDF和量測數據下,狀態估計就是對系統JPDF的最大后驗估計[13](MAP)。系統狀態變量的最大后驗估計可表示為:
(9)
然而,由式(8)可知,狀態估計系統的JPDF是由不同時刻的狀態分布和不同傳感器的量測分布共同組合的變量眾多、形式相當復雜的全局函數,對其進行MAP求解相當困難。考慮到動態系統中的每一個狀態轉移過程和量測過程都是全局函數的一個分解因式,是一個局部函數,這與因子圖模型所表示的數學含義高度一致;因此可以考慮使用因子圖模型對狀態估計系統的JPDF進行表示(見圖2),進而使用因子圖模型的分治策略簡化JPDF的MAP求解。

圖2 估計系統的JPDF的因子圖模型表示
由圖2所示,圖中用變量節點表示系統待估計的狀態,用因子節點表示先驗信息、狀態轉移和量測過程。利用因子圖模型對估計系統的JPDF進行表示,可以直觀地反映動態系統的動態演化過程和每個狀態對應的量測過程。
同時,圖形化的表示使系統具有更好的通用性和擴展性:
(1) 系統每進行一次狀態轉移就等價于在因子圖模型中增加一個變量節點;
(2) 系統每增加一個量測信息就等價于在因子圖模型中增加一個因子節點;
(3) 甚至當某種量測方式建立的是系統不同時刻狀態間的關系,也可以使用一個因子節點將2個狀態連接起來,進而在因子圖中形成一個閉環。
反之,當系統不需要對某個狀態進行估計或不使用某個量測信息時,等價于在因子圖中刪除相應的節點。
3 基于因子圖的狀態估計求解
對動態系統的JPDF進行MAP估計時,由于JPDF是多個過程分布函數的連乘形式,如式(8)所示,直接求解較為困難,可以考慮對式(8)進行取對數操作,從而得到式(9)的等價形式如下:
(10)
(11)
若定義代價函數gk為:
(12)
則系統的狀態估計可等價為全局代價函數的聯合優化:
(13)
顯然,式(13)是一種最小二乘的表示形式,由于系統模型fk和量測模型hk通常存在一定的非線性,所以式(13)描述的是一個非線性最小二乘求解問題。

(1) 對于狀態模型
(14)
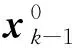
其中:
(15)
(2) 對于量測模型
{Hkδxk}-ck
(16)

其中:
(17)
(18)
式中:Δ={δxi},為對當前系統變量Xk的更新增量。
顯然,式(18)表示的是一個典型的線性加權最小二乘問題。
(19)

(20)

(21)

綜上所述,可以給出基于因子圖的狀態估計方法中全局代價函數g(Xk)求解的高斯-牛頓迭代優化方法流程,如圖3所示。

圖3 高斯-牛頓非線性迭代優化算法框架
由此可得全局代價函數g(Xk)的迭代優化求解流程,如下所示:
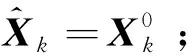

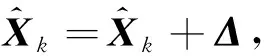
(5) 優化完成,最新的線性化點即為優化求解的狀態。
圖4給出了基于因子圖狀態估計方法的流程圖。

圖4 基于因子圖狀態估計方法流程圖
如圖5所示,進一步認為系統雅克比矩陣J(Xk)是因子圖的一種線性化表示形式,它的塊結構反應了因子圖的節點結構:J(Xk)矩陣中的每一行(行塊)代表了一個量測過程的代價函數,矩陣中的每一列代表了一個導航狀態變量。圖中P(z3|x1,x3)節點表示的量測方程建立了2個不同時刻狀態間的約束關系,這在基于因子圖的狀態估計方法中是普遍適用的。
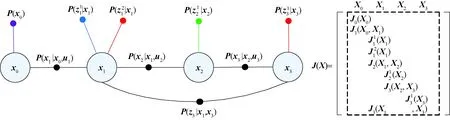
圖5 一個典型動態系統的因子圖與對應的雅克比矩陣
4 結束語
基于因子圖的動態系統狀態估計方法將系統的JPDF用一個因子圖模型表示;進而利用因子圖模型的分治策略將JPDF的MAP轉化為一個全局代價函數聯合優化;最后對全局代價函數進行線性化和歸一化等價,將估計問題轉化為最小二乘方程組的求解問題。與此同時,因子圖模型的二元節點結構簡明直觀,便于系統的快速構建和靈活擴展,特別適用于量測信息頻繁切換的動態系統。另一方面,基于因子圖的估計問題可以將歷史時刻的狀態都作為估計狀態,雖然增加了估計問題的計算量,但是也能充分利用量測信息對當前狀態進行估計,對歷史估計進行平滑,也能利用歷史狀態對當前狀態進行估計。
但是,基于因子圖的狀態估計中系統每接收到一個量測,因子圖中就會增加相應的因子節點,這等價于在被線性化的量測雅克比矩陣和右手項增加一行新數據。但隨著動態系統時間的推移,系統的狀態和量測不斷增加,系統對應因子圖模型的因子節點和變量節點數目也不斷增加。當求解方程組的維數快速增加時,聯合優化求解的計算量會急劇增加,使實時性難以得到保證。針對基于因子圖狀態估計方法實時性的常見快速解決方法包括區間平滑法、“矩陣稀疏分解”法和增量平滑算法等,可根據具體實際問題選取適當的快速求解方法。

