寬波束雷達測高算法
肖 雷,周秀珍
(中國船舶重工集團公司第七二三研究所,江蘇 揚州 225101)
0 引 言
隨著現代軍事工業的迅速發展,雷達高度計在導彈的制導過程中起著重要作用,現在的雷達高度計主要分為脈沖雷達高度計和調頻連續波(FMCW)雷達高度計兩大類[1]。根據雷達發射波束角的寬度,脈沖雷達高度計可以劃分為寬波束與窄波束2種。在平臺穩定、指向不變的情況下,窄波束雷達相比較寬波束雷達來說,測量精度更高,因此在實際應用中,窄波束雷達高度計相較寬波束雷達高度計而言,其應用更加廣泛。但是由于彈載雷達平臺不穩定,在這種條件下,窄波束雷達高度計不能保證波束能夠準確指向雷達天底點,因而在彈載雷達領域,須采用寬波束雷達高度計。
與點目標信號的模擬不同,寬波束雷達高度計的目標模型為地面。在此背景下,介紹了3種雷達測高算法,并設計仿真流程完成了對3種雷達測高算法的仿真實現,對仿真生成的回波進行測高,將測高結果與高程圖的真實高度進行對比,最終對3種算法的測高精度進行了比較。
1 脈沖雷達回波仿真模型
回波功率仿真和相干視頻回波仿真是現代雷達回波仿真中比較常見的2種方法,回波功率仿真只關注功率大小,而相干視頻回波仿真主要關注的是信號的相位信息。
1.1 相干視頻回波模型
如果雷達的發射信號表示為:
ψT(t)=VT(t)ej2πfct
(1)
式中:VT(t)表示為矩形包絡。
而ψT(t)又可以表示為:
(2)
式中:Tt為發射信號脈寬。
如果從雷達發射信號到接收回波的這段時間里天線指向、地面散射特性、位置沒有變化,且不忽略頻率的多普勒變化,則由雷達方程可推出點目標的回波方程為:
(3)
(4)
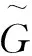
γ和目標散射截面積σ的關系可表示為:
(5)
將式(1)、式(4)、式(5)代入式(3)中,可得到雷達的單個散射單元回波信號為:
(6)
由于大部分自然地形都是粗糙的表面,散射元回波相位并不十分精確,需要在式(6)基礎上加上一個相位的隨機分量φ,φ的概率密度為:
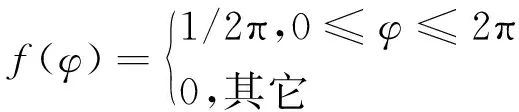
(7)
最后得到的散射單元相干視頻回波表達式如下:
(8)
1.2 功率疊加回波模型
由雷達方程可推出單個散射目標的回波功率如下:
(9)
經研究[2],在粗糙地面的假設條件下,雷達地面回波總功率的期望值等于照射區域內各個散射單元回波功率的期望值之和:
(10)
地面回波的功率模型可由以上這個原理計算得出。
2 雷達測高算法
2.1 回波前沿雷達測高半功率點算法
回波前沿的雷達測高半功率點算法是把雷達天底點位置反射的回波和回波前沿的半功率點位置相對應。由此可以通過半功率點相對于回波上升沿起點的時間延時τH來解算出天底點的高度:
(11)
式中:c為光速。
2.2 偏差重心雷達測高跟蹤算法
偏差重心(OCOG)雷達測高跟蹤算法的基本思路是首先須定義一個矩形跟蹤窗口,然后用一個與窗內回波重心相同、面積相同的矩形和窗內的回波進行擬合,通過調整跟蹤窗使波形中心和矩形中心重合,最后矩形寬度的一半加上跟蹤窗中心就是跟蹤點。假設矩形的幅度為A,矩形的寬度為W,E為誤差量,由此得出它們的計算公式:
(12)
(13)
(14)
(15)
通過誤差量E來調整跟蹤窗的位置,直至誤差等于零,這時跟蹤窗的中心位置與W/2之和就是跟蹤天底點的時延。
2.3 平均高度雷達測高算法
平均高度雷達測高算法的基本思路是:某時刻的回波功率可以通過一定空間距離之內所有散射元在這一時刻回波功率的疊加來表示,通過計算雷達的平均距離和這些散射元就可以得到平均高度。
可計算得出平均高度:
(16)
式中:PR(i)代表回波功率的采樣。
3 3種雷達測高算法實現
對上面介紹的3種雷達測高算法,下面分別給出了其實現的流程圖,如圖1、圖2、圖3所示。
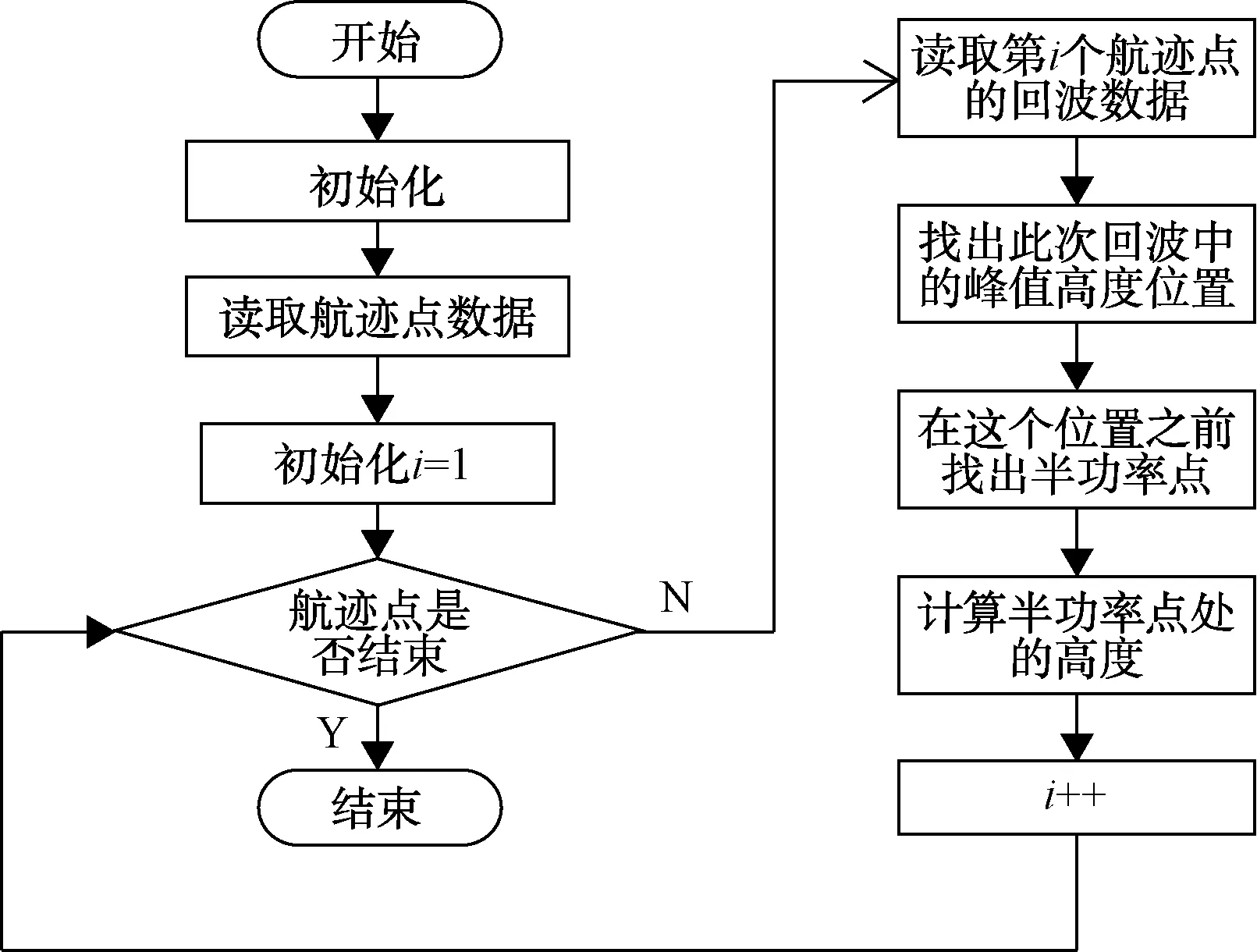
圖1 半功率點雷達測高算法流程圖
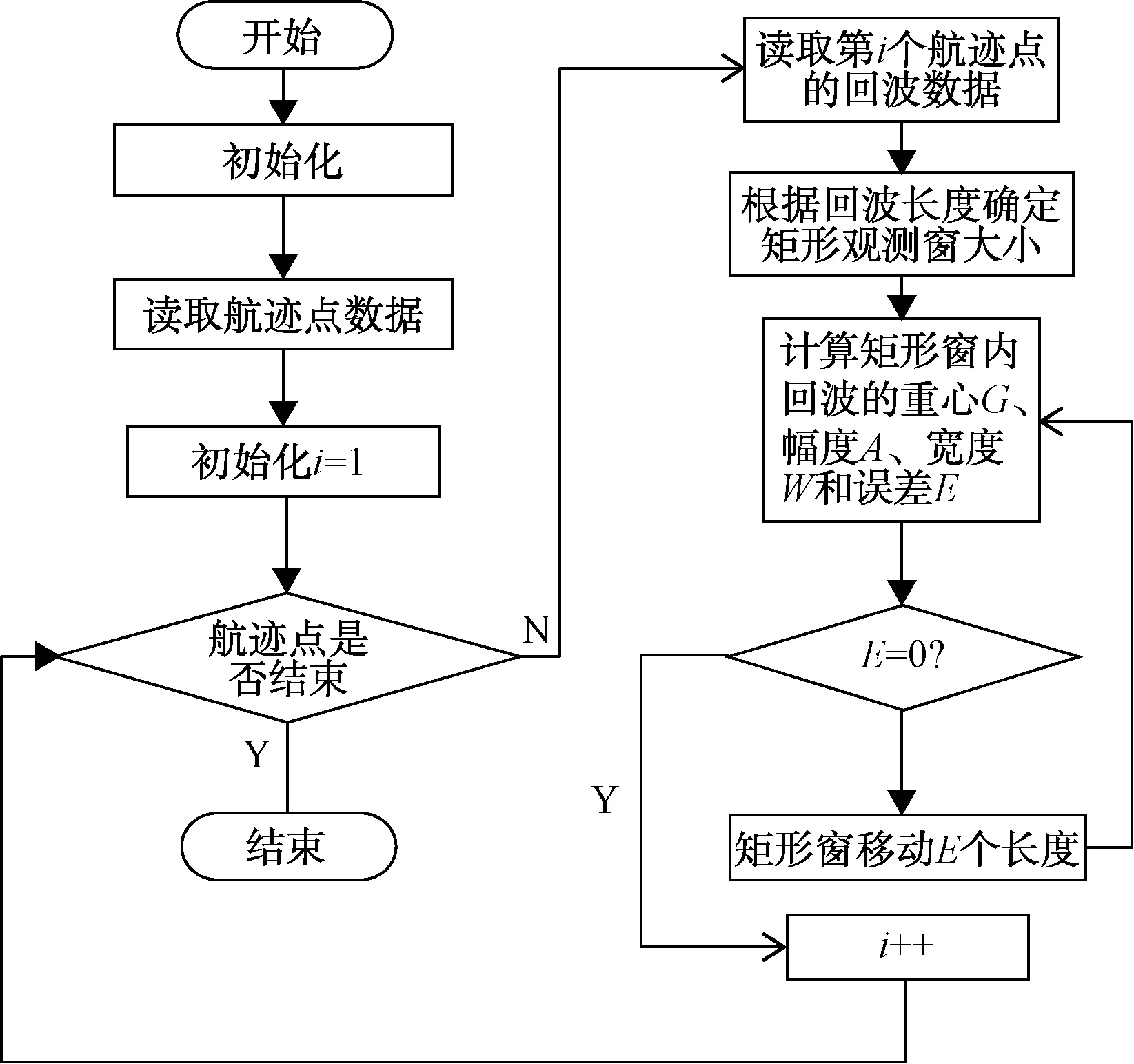
圖2 OCOG雷達測高算法流程圖
4 仿真結果及分析
選取出50個雷達的航跡點,分別通過上面介紹的3種雷達測高算法可以計算出高度,之后再與真實的地形數據進行比較,計算出3種雷達測高算法的誤差,仿真結果如圖4所示。
圖3 平均高度雷達測高算法流程圖
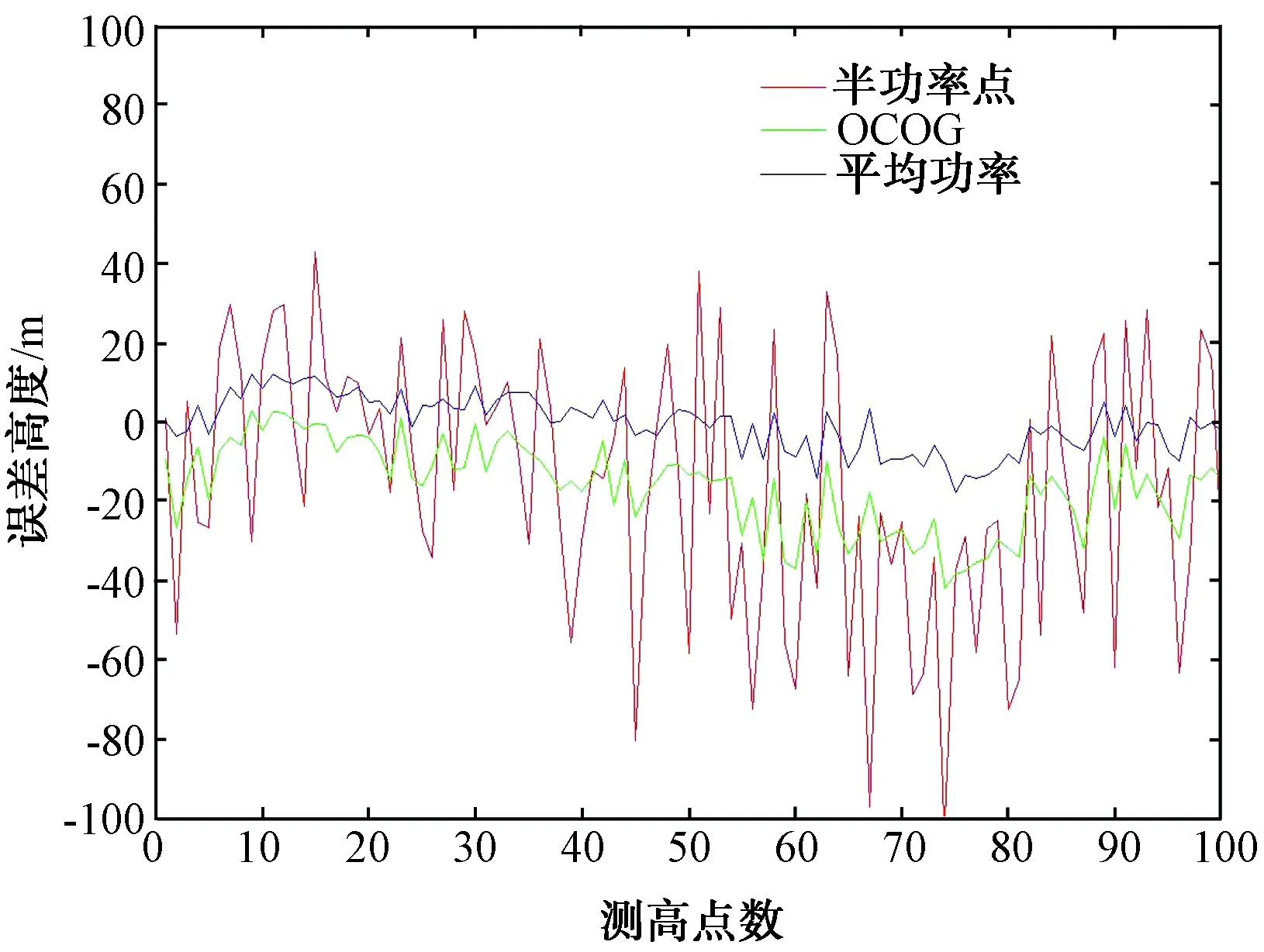
圖4 3種雷達測高算法誤差高度
由圖4可以觀察出寬波束雷達高度計在復雜地形的回波,其中半功率點雷達測高算法會引起比較大的誤差,而平均高度雷達測高算法和偏差重心雷達測高跟蹤算法能更好地估計出雷達高度,其中平均高度雷達測高算法的估計精確度最好。

