格點多邊形遇上畢克公式
李沁霖
“丁零零……”下課了!悠悠急匆匆地跑來,說:“小霖啊,現在的題目真是麻煩。你看這個圖形(圖1),已知每一個小正方形的面積均為1平方厘米,求陰影部分四角形的面積。這怎么求呀?”
我接過題目仔細一瞧,呵呵笑道:“這個題目其實不難。把圖形分割成我們熟悉的正方形和三角形(圖2),那么四周每個小三角形的面積是2×2÷2=2(平方厘米),中間正方形的面積是2×2=4(平方厘米),所以四角形的面積為2×4+4=12(平方厘米)。”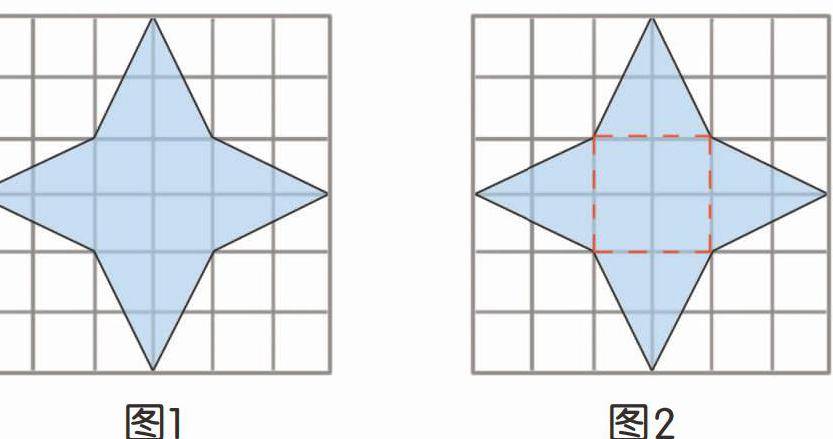
悠悠點點頭,說:“是哦,這樣一分割就簡單了!”
“其實啊,這個題目還有更簡單的解決方法。那就是根據它內部格點數和周界上的格點數,得出四角形的面積是9+8÷2-1=12(平方厘米)。看,是不是簡單了許多?”
她不可置信地說:“啊,這怎么可能?這是為什么呢?”
我神秘地一笑,說:“這類題目呢,就是格點問題。一個多邊形的頂點如果全是格點,這個多邊形就叫格點多邊形。這種格點多邊形的面積計算起來其實不難,一般有三種方法。你知道是哪三種嗎?”
一旁的晴晴笑著湊過來,說:“我知道!規則的格點多邊形,可以運用多邊形的面積公式求出面積;而一些簡單而又特殊的格點多邊形,可以通過數格子求出面積。但是數格子的方法比較原始,很少用。”
“那還有一種方法是什么呢?”悠悠忙追問道。
晴晴不慌不忙地回答:“較復雜的不規則格點多邊形,一般用畢克公式計算。對任意格點多邊形,只要數出多邊形周界上格點的個數及圖內格點的個數,就可以用畢克公式算出面積:格點多邊形面積S=圖內格點個數N+周界格點數L÷2-1,即S=N+L/2-1。
“我好像懂了。”悠悠興奮地點點頭。
我隨即說道:“那我們來做道題熱熱身吧!”說罷,我便在紙上畫了一個格子圖。
悠悠想了想,立即報出了答案:“內部格點數2個,周界上格點數20個,面積為2+20÷2-1=11(平方厘米)。”
“不錯,就是這樣。”我點了點頭。
悠悠感嘆道:“數學真是奇妙呀!之前覺得很難的圖形題,現在因為這些不可思議的方法又覺得很有意思。”
數學真是無處不在,同一道題目可以有不同的解法,我們要善于思考,勤于動腦,發現每一個小細節。
馮煜琪7月7日 10:10:22
原本看起來很難的題目,經過小霖這么一講,立馬就變簡單了!
朱菲揚 7月7日 11:35:12
這么難的題目都能輕松解答,真厲害!
黃煦婷7月7日 11:40:25
小霖用簡單易懂的方法告訴我們如何求解格點多邊形面積,讓我受益匪淺。
徐銘蔚7月7日 12:22:43
數學中藏著奧秘,小霖巧妙的解題方法讓我豁然開朗,激發了我探索數學奧秘的興趣。

