荔枝園智能灌溉決策系統模糊控制器設計與優化
謝家興 高 鵬 莫昊凡 余國雄,3 胡 潔 王衛星,4
(1.華南農業大學電子工程學院, 廣州 510642; 2.廣東省智慧果園科技創新中心, 廣州 510642; 3.中國移動通信集團廣東有限公司, 江門 529030; 4.廣東省農情信息監測工程技術研究中心, 廣州 510642)
0 引言
我國荔枝種植總面積60萬hm2,占世界荔枝總面積的75%;荔枝總產量190.66萬t,占世界荔枝總產量的47.78%,占世界生產總值的57.75%以上,目前仍呈增大趨勢[1-2]。荔枝園主要采用的傳統漫灌技術對水資源造成較大浪費[3-7]。同時,荔枝園所處環境復雜,受光照、土壤濕度、空氣濕度、降雨等條件影響,由人為主觀意識產生的判斷有較大不確定性及誤差,易造成較大經濟以及資源浪費。因此,開發一種荔枝園智能控制系統對荔枝園進行現代化管理,以最大化節約資源,勢在必行。
目前,郭正琴等[8]設計了基于模糊控制的智能灌溉控制系統,楊翠翠[9]設計了基于無線網絡的環境監測與智能控制灌溉系統,張曉光等[10]設計了節水灌溉的模糊系統,高玉芹[11]設計了基于ZigBee和模糊控制決策的自動灌溉系統。以上系統僅設計了基本模糊控制器,而基本模糊控制器穩態性能低,存在穩態誤差等。基于此,本文設計基于模糊控制技術的荔枝園智能灌溉決策系統,對基本模糊控制器進行優化,提升其控制精確度與穩定性,對所接收數據進行更好的決策和控制。
1 智能灌溉模糊控制軟件設計
模糊專家決策系統接收傳感器節點采集的土壤含水率數據,根據專家系統的模糊規則實時推理出灌溉量,進行灌溉。
對荔枝園灌溉環境分析可得,用于荔枝智能灌溉的模糊專家系統為多維的模糊控制專家系統,根據灌溉過程中的人為經驗,將專家的經驗、知識庫抽象化為模糊控制中的模糊規則,選擇不確定性推理的確定性模型作為本專家系統的推理機,該模型簡單實用,已被應用到一些實用的專家系統之中[7]。模糊專家決策系統的模糊控制流程圖如圖1所示。
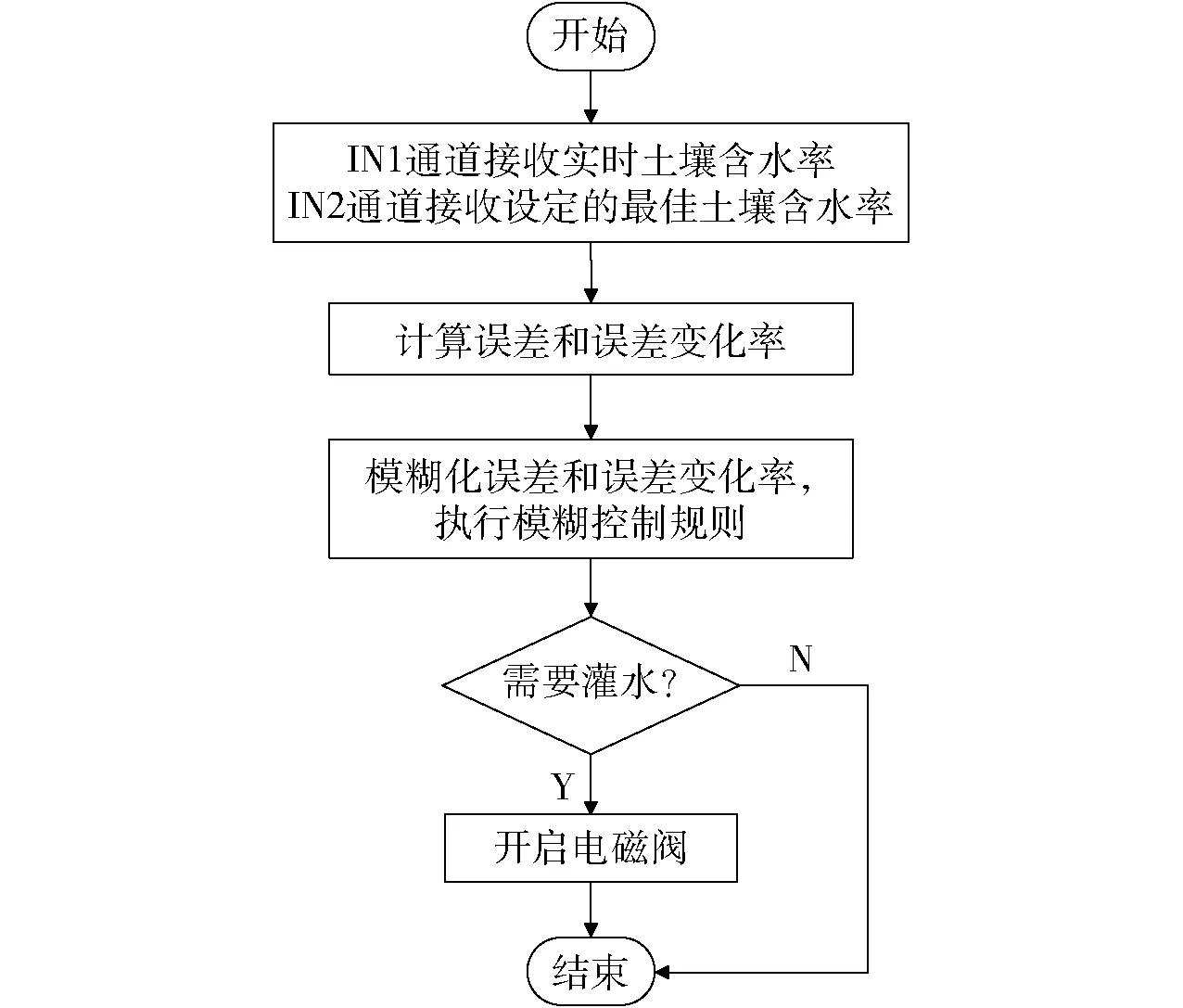
圖1 模糊控制流程圖 Fig.1 Flow chart of fuzzy control
荔枝園中的環境信息包括溫度、空氣濕度、光照度和土壤含水率等,影響荔枝生長的關鍵因素是土壤含水率。在實際灌溉中,通常根據土壤含水率來決定荔枝是否需要灌溉。
荔枝在不同生長周期里所需的土壤最佳含水率均有所不同,所以本系統在確定荔枝的生長周期后,選用該周期土壤最佳含水率與土壤實測含水率的差E,及其誤差變化率EC為2個輸入變量,土壤需水量U作為其輸出量,后將E和EC輸入模糊控制器進行模糊化控制,通過模糊決策產生灌溉指令來控制灌溉執行機構,實現灌溉。其中,模塊K1、K2、K3起調幅作用,確保系統的穩定性,其總體結構如圖2所示。

圖2 荔枝園智能灌溉系統總體結構圖 Fig.2 Overall structure diagram of intelligent irrigation system in litchi orchard
2 智能灌溉模糊控制器設計
2.1 理論基礎
模糊控制器是以模糊集合理論和模糊推理為基礎,模擬人的思維方式,能總結豐富的操作經驗,從而用自然語言表述控制策略或者通過大量實際操作歸納總結出多個控制規則,并用計算機實現自動控制[12-14]。模糊控制是一種非線性控制方法,無需建立精確的數學模型,魯棒性強,非常適合時變以及滯后系統的控制[15]。
2.2 模糊控制器設計
2.2.1模糊語言變量設計
根據荔枝園灌溉專家經驗及周邊環境對荔枝灌溉的影響,確定控制量為土壤濕度、降雨量、空氣濕度等,由于土壤含水率可以反映土壤中水分的含量,而水分是作物生長不可或缺的因素之一,因而土壤含水率可以作為判斷作物缺水與否的最佳條件[16-17]。本文選用給定土壤最佳含水率與土壤實測含水率的差E及其誤差變化率EC為兩個輸入變量。
為了提高控制精度,設置多個語言變量。其中誤差E和輸出變量U的模糊語言值設定為9個,即{NB(負大),NM(負中),NS(負小),NW(負微),ZO(零),PW(正微),PS(正小),PM(正中),PB(正大)},EC的模糊語言值設定為7個,即{NB(負大),NM(負中),NS(負小),ZO(零),PS(正小),PM(正中),PB(正大)}。E的基本論域為{-15,15},模糊論域D為{-6,-4,-2,0,2,4,6},EC的基本論域為{-10,10},模糊論域X為{-6,-4,-2,0,2,4,6},U的基本論域為{-15,15},模糊論域Y為{-10,-7.5,-5,-2.5,0,2.5,5,7.5,10}。表1是用Matlab軟件模糊控制工具箱設計的模糊控制規則表。
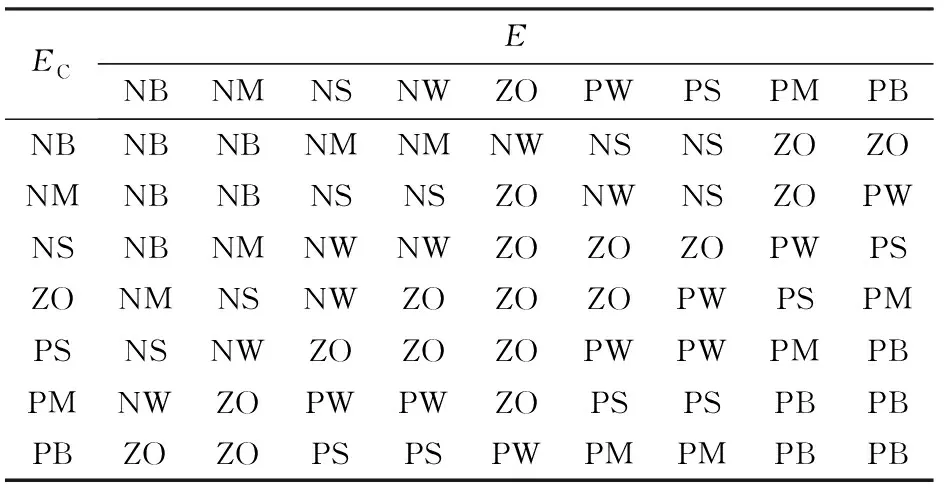
表1 模糊控制規則 Tab.1 Rules of fuzzy control
誤差的量化因子Ke、誤差變化率的量化因子Kec和控制量的比例因子Ku的計算公式為
(1)
(2)
(3)
式中n1、n2、m——誤差E、誤差變化率EC、輸出變量U的模糊論域最大值
emax、ecmax、umax——誤差E、誤差變化率EC和輸出變量U的基本論域最大值
計算結果為Ke=0.4,Kec=0.6,Ku=1.5。
選擇隸屬函數時,因三角形隸屬函數有簡化計算、易于實現的特性,模糊語言變量模糊化的隸屬函數類型選擇以簡單的三角形為主。在誤差變量E中還增用了梯形。三角形、梯形隸屬函數的解析表達式為
(4)
(5)
其中a、b、c、d均為確定形態的重要參數,且a≤b≤c≤d。
具體隸屬函數分布如圖3~5所示。
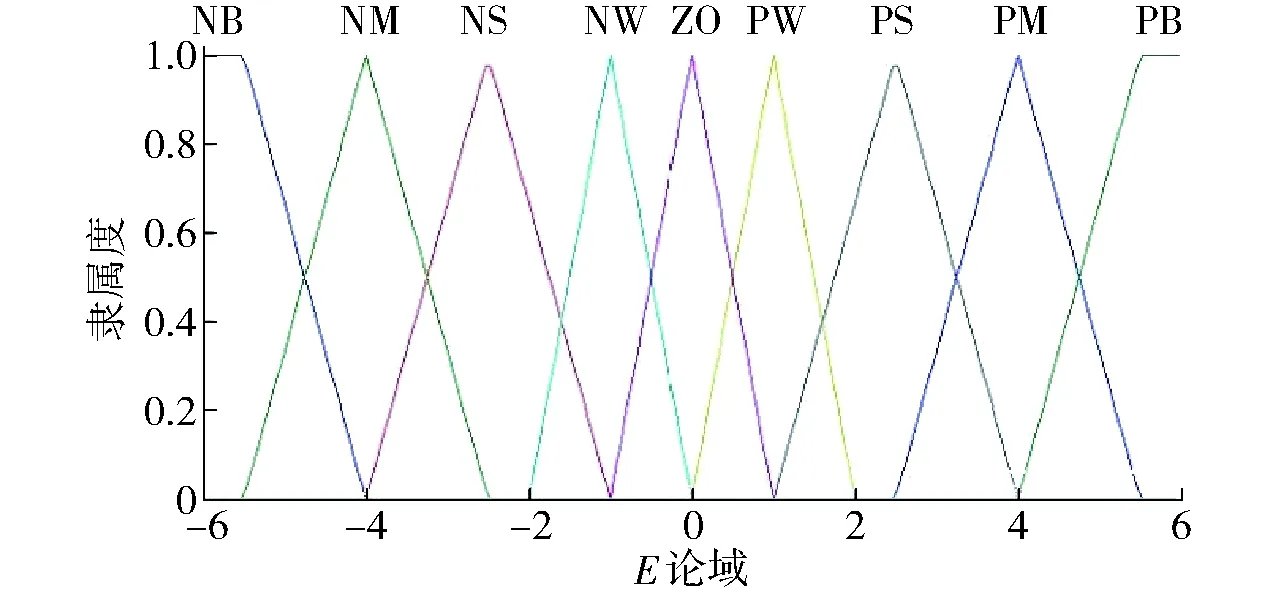
圖3 誤差變量E的隸屬函數 Fig.3 Membership function of fuzzy variables E error
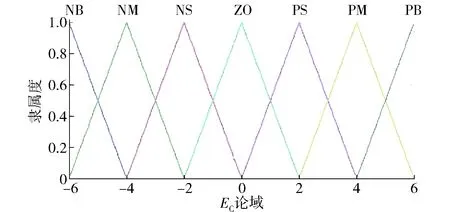
圖4 誤差變化率EC的隸屬函數 Fig.4 Error rate membership function of fuzzy variables EC
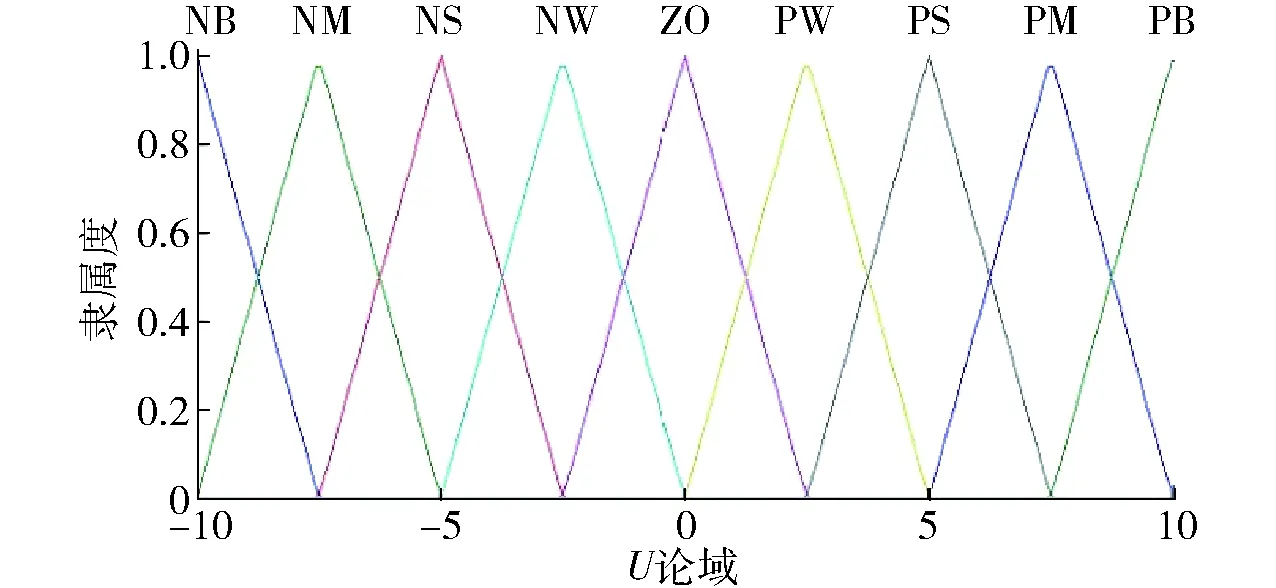
圖5 輸出變量U的隸屬函數 Fig.5 Output membership function of fuzzy variables U
2.2.2模糊規則設計
根據灌溉經驗與實測數據,制定出模糊推理規則,規則采用IF-THEN語句,例如,if (EisA) and (ECisB),then(UisC)。其中,A、B、C分別是誤差E、誤差變化率EC和控制量U論域在X、Y、Z方向上的模糊集。模糊控制表的設計原則為:當誤差較大時,控制量的變化應盡量減少誤差;當誤差較小時,在消除誤差外,需要同時考慮系統的穩定性,避免系統產生超調,甚至震蕩,確保其穩定性[18]。其詳細規則如表1所示。
2.2.3反模糊化
反模糊化是將根據模糊規則決策后的模糊量轉換為清晰量的過程,反模糊化的方法有面積重心法、面積平分法、最大隸屬度法。其中,面積重心法直觀合理,計算數據精確,故本文采用面積重心法進行反模糊化。面積重心法即求出模糊集合隸屬函數曲線和橫坐標包圍區域面積的中心,選該點對應的橫坐標Ucen作為該模糊集合的代表值。若論域U={u1,u2,…,un},uj處的隸屬度為A(uj),則Ucen的計算公式為
(6)
2.2.4模糊控制器的輸出
運用Matlab軟件的Simulink工具箱對模糊控制進行仿真。根據建立的模糊庫,可以得到如圖6所示的模糊規則曲面圖。從圖6可以看出輸入、輸出變量的關系,土壤含水率低,所需灌溉量增加,而土壤含水率較高,則所需灌溉量相應減少。
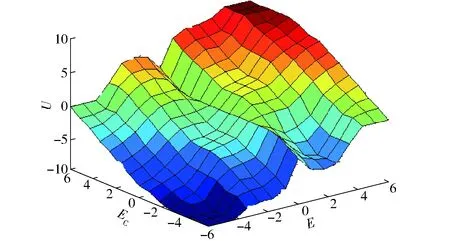
圖6 輸入、輸出變量關系曲面圖 Fig.6 Input-output variable relation surface graph
3 仿真與試驗
3.1 仿真模型
假定由執行機構和被控對象組成的灌溉系統廣義對象的數學模型為典型二階環節[19],其數學表達式為
(7)
利用Matlab中的Simulink工具箱,構建二維模糊控制系統仿真模型,如圖7所示。
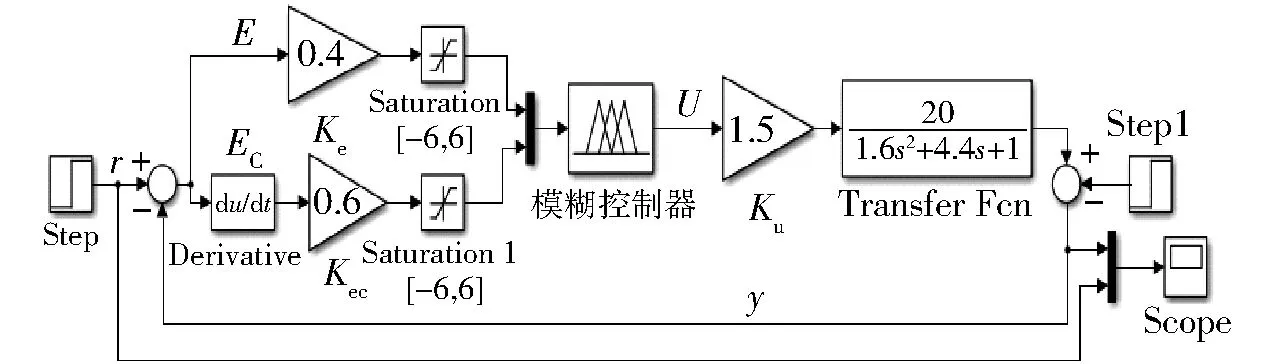
圖7 二維模糊控制系統仿真模型 Fig.7 Simulation model of basic fuzzy control system
下面對模糊控制和PID控制的控制性能進行分析比較。對同樣的被控系統,建立PID控制,對于該二階系統,根據多次試驗得整定PID控制的參數Kp=0.284,Ki=0.03,Kd=0.626,設置階躍信號產生時間為1 s。具體的PID控制器系統仿真圖如圖8所示。在PID控制和模糊控制系統中分別在40 s時以幅值0.3 V的階躍信號作為干擾信號,仿真時間改為60 s,仿真結果如圖9所示。
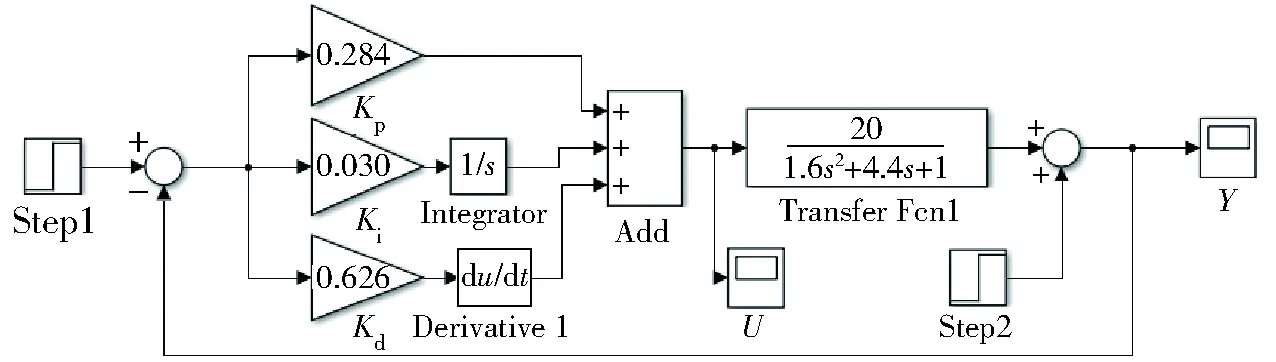
圖8 PID控制器系統仿真圖 Fig.8 PID controller system simulation diagram
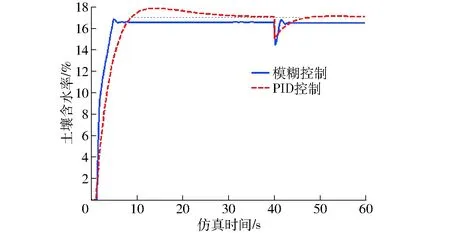
圖9 PID與模糊控制仿真比較 Fig.9 Comparison of PID and fuzzy control simulation
在40 s處加入干擾信號可比較兩種控制器的抗干擾性,由仿真結果可得出仿真數據,如表2所示。
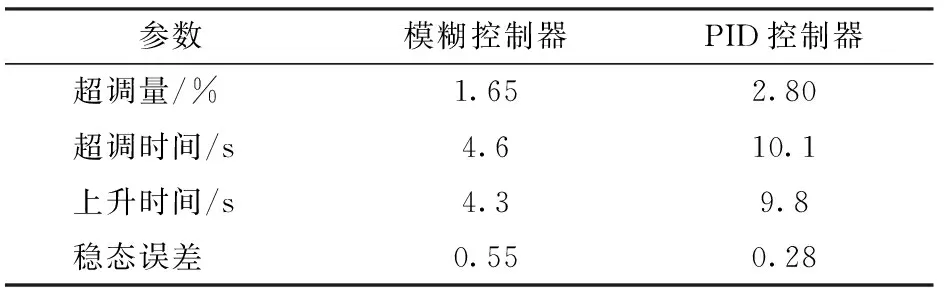
表2 模糊控制器與PID控制器性能指標 Tab.2 Performance index between fuzzy controller and PID controller
由表2可得,模糊控制器和PID控制器都可以實現對被控系統的控制。PID控制超調量大,調節時間長,動態性能差,但控制精度較高,模糊控制則相反,動態性能好,基本沒有超調,受到干擾后在更短的時間將信號調整到正常值,即具有更強的抗干擾性。但存在模糊化而引起的穩態誤差,總體性能較PID控制器更適應本系統。
3.2 果園試驗
為驗證該系統的有效性,本文選取華南農業大學園藝學院荔枝園進行實地試驗,試驗現場采集數據的傳感器節點如圖10所示。

圖10 傳感器節點 Fig.10 Sensor node
在荔枝園內的2個區域進行系統智能灌溉性能測試,其中一個區域(A區)部署一個傳感器節點和一個電磁閥節點,傳感器節點和電磁閥節點采用相同的PCB板,區別為傳感器節點外接土壤含水率傳感器,電磁閥節點外接雙穩態脈沖電磁閥模塊,實物圖如圖11所示。

圖11 PBC板、傳感器和電磁閥模塊實物圖 Fig.11 Sensor and solenoid valve nodes
傳感器節點每隔30 min監測一次土壤含水率,并智能控制電磁閥對荔枝樹的灌溉。另一個區域(B區)部署一個傳感器節點,用來監測該區域的土壤含水率,但不灌溉。其中土壤含水率17%為荔枝樹生長最佳環境。2016年4月7—24日土壤含水率如表3所示。
由表3可知,在試驗期內,A區通過智能灌溉方法,使得該區的土壤含水率平均值為17.85%,均高于荔枝生長的最佳土壤含水率的下限(15.55%),達到預期灌溉效果[20-21],并且高于B區土壤含水率平均值7.75%。A區每次灌溉時,其土壤含水率均會迅速上升,然后緩慢下降,說明系統根據模糊規則及時調節土壤濕度,有較強實時性,反應速度快,較好地滿足了荔枝生長的需要。
3.3 模糊控制器優化仿真
Simulink仿真的本質是利用某種求解器對系統狀態方程進行求解。S函數能夠接收來自Simulink求解器的相關信息,并對求解器發出的命令作出適當的響應,這種交互作用類似于Simulink系統模塊與求解器的交互作用。Simulink設計了固定格式的S函數接口,通過S函數可將系統的數學方程表達式與方框圖表達形式聯系起來[22-25]。顯然,S函數是整個Simulink動態系統的核心。
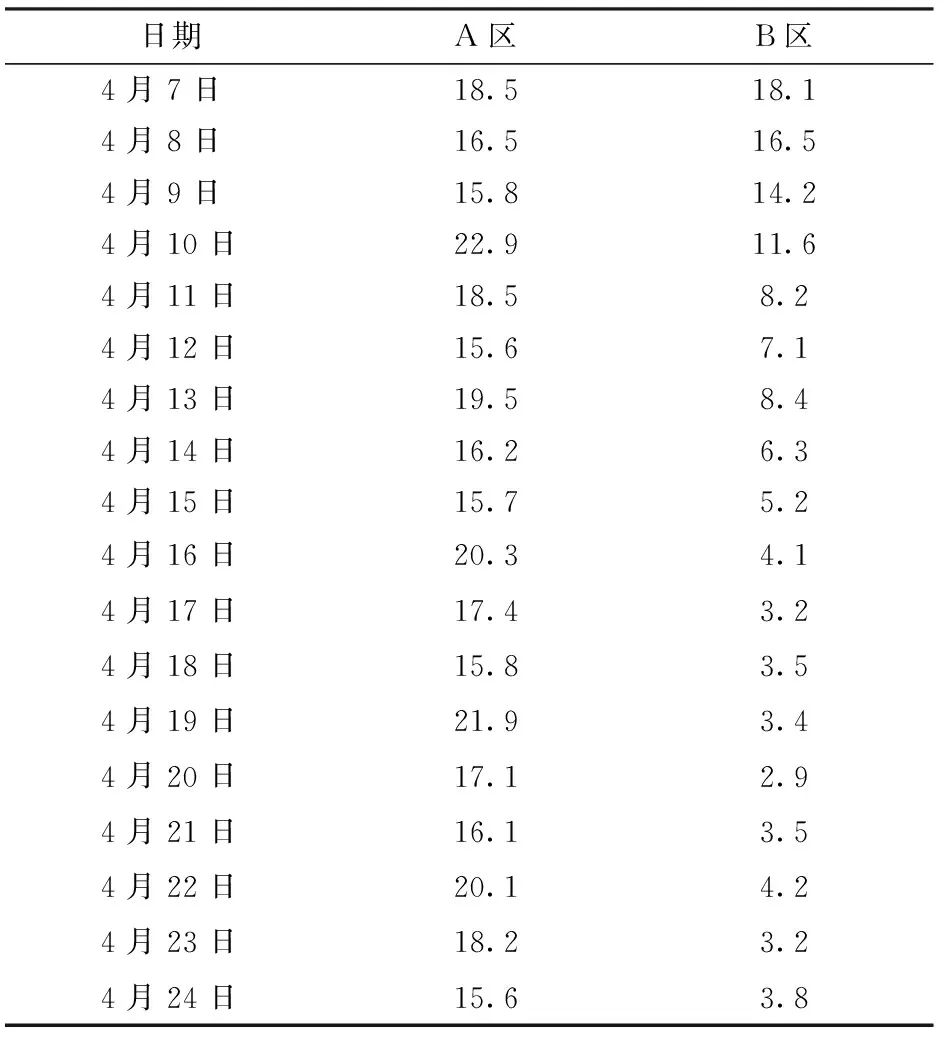
表3 土壤含水率 Tab.3 Soil moisture content data %
在多次仿真中,可得出誤差較大時,選擇較小的Ke和Kec,減小誤差分辨率,而選擇較大的Ku,加快系統響應;隨著誤差變小,Ke和Kec逐漸增大,而Ku逐漸減小。
仿真時,將S函數模塊填入該文件,與Simulink工具箱中特定工具組成S函數模塊,如圖12所示。
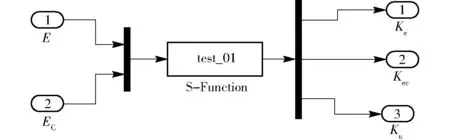
圖12 S函數模塊 Fig.12 S function module
將該模塊與模糊控制器對接,組成優化后的模糊控制器及參數自調整模糊控制系統,如圖13所示。其工作流程與上文所述的模糊控制器相似,其不同點為該模糊控制器通過S函數實現了量化因子和比例因子自調整,提高了模糊控制器性能,使其決策更精確。
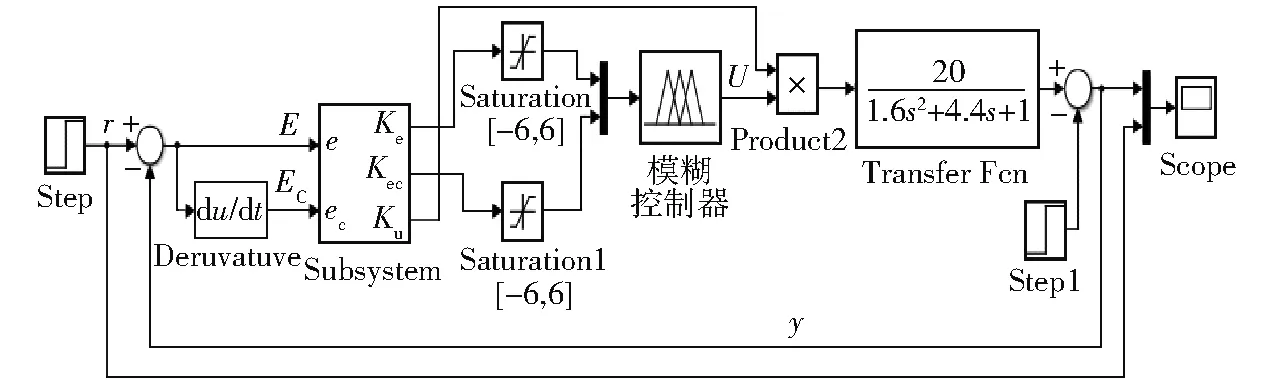
圖13 參數自調整模糊控制系統仿真圖 Fig.13 Parameter self-tuning fuzzy control system simulation diagram
對上文的模糊控制器和用S-函數優化的模糊控制器進行以同樣的階躍信號為輸入,并分別在20 s時以幅值為0.3 V的階躍信號作為干擾信號,進行仿真,對兩種模糊控制器的控制性能進行比較,如兩種模糊控制器進行控制時的超調量、超調時間、上升時間、穩態誤差和抗干擾性。比較結果如圖14所示。
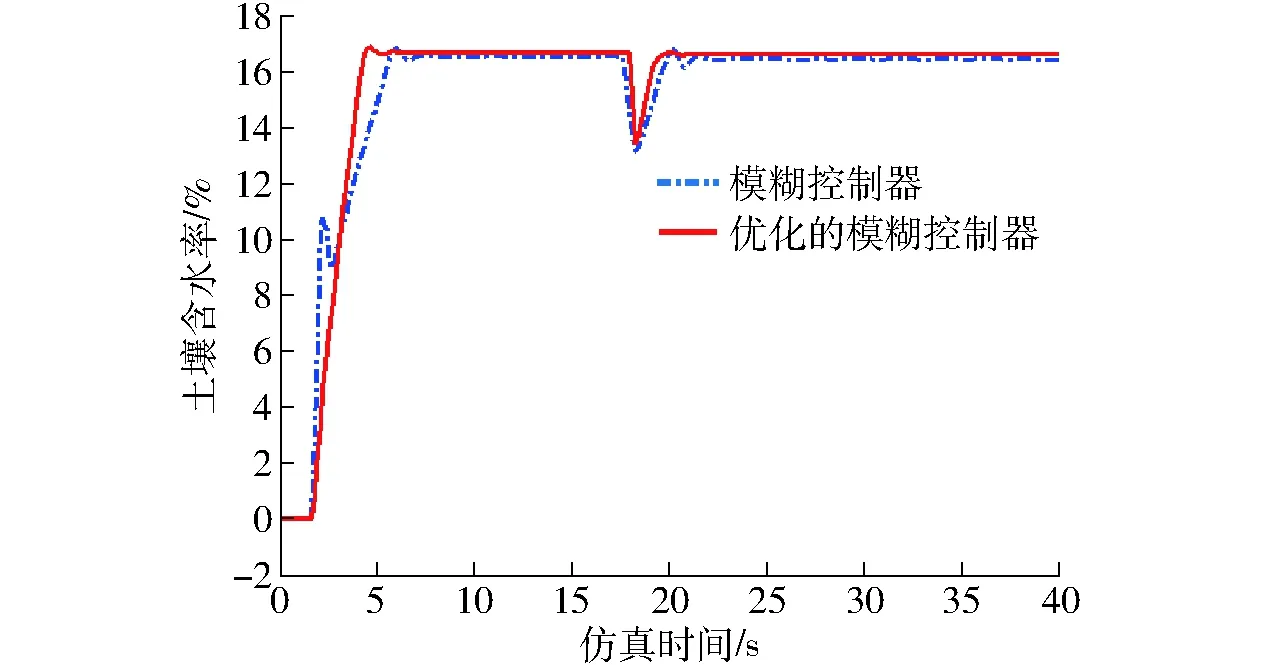
圖14 模糊控制器與優化后的模糊控制器性能比較 Fig.14 Performance comparison between general and parameter self-tuning fuzzy controller
由仿真結果得到經S函數優化后的參數自調整模糊控制器的暫態性能指標,如表4所示。
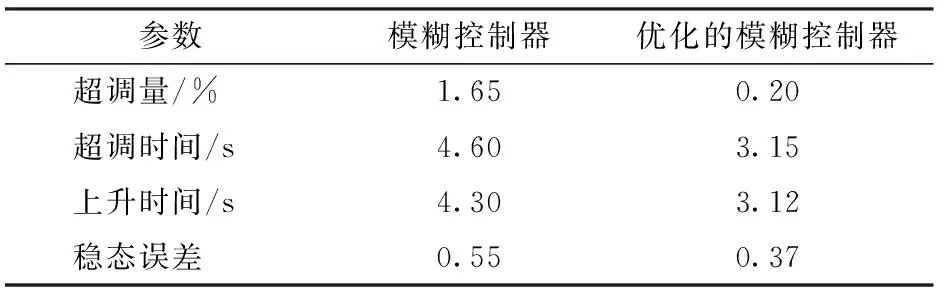
表4 模糊控制器與S函數優化的參數自調整模糊 控制器性能指標 Tab.4 Performance index between fuzzy controller and parameter self-tuning fuzzy controller of S function optimization
由表4可知,用S函數優化的模糊控制器具有較好的暫態性能,如超調量基本趨近于零;較短的超調時間和上升時間;該模糊控制器具有更小的穩態誤差;受到干擾后在更短時間內將信號調整到正常值,即具有更強的抗干擾性。
綜上所述,用S函數優化的參數自調整模糊控制器的控制精度更高,能提升灌溉模塊控制系統的控制性能。
3.4 優化模糊控制灌溉系統田間試驗
在試驗場地C另加一組試驗,該試驗場地器材布置、場地環境、土壤環境均與3.2節所述的場地A、B試驗環境相同,進行另外一組智能灌溉控制與監測試驗,驗證利用S函數優化的模糊控制灌溉系統的性能。其監測結果如表5所示。
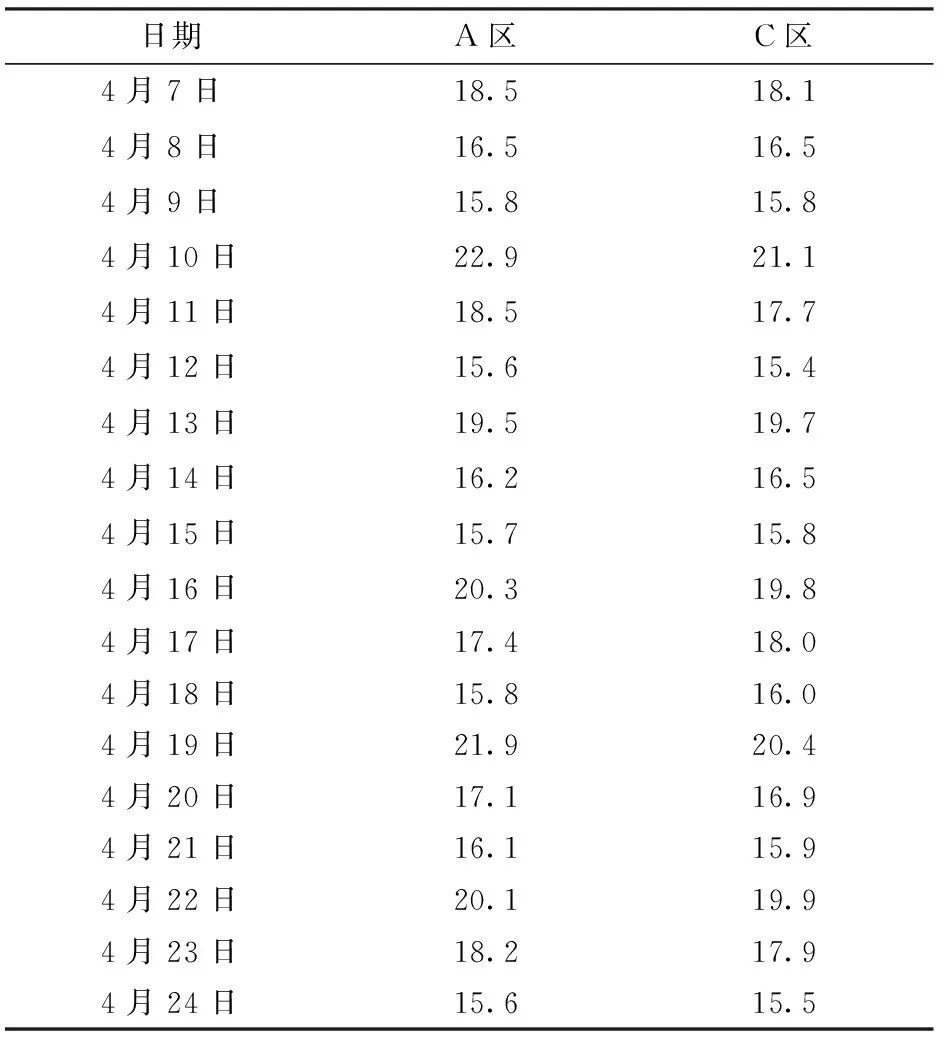
表5 A、C區土壤含水率比較 Tab.5 Comparison of soil moisture content data %
由表5可知,C區采用優化后的模糊控制灌溉系統的智能灌溉方式,土壤含水率的平均值為17.6%,相比優化前模糊控制灌溉系統的灌溉結果,優化后的模糊控制灌溉系統具有更強的穩定性、抗干擾性以及更高的控制精度,并且,在試驗中發現,采用優化后的模糊控制灌溉系統,接收到土壤含水率數據之后能更快地調節土壤含水率使土壤含水率接近土壤最佳含水率并趨于穩定,其性能有了明顯提高。
4 結束語
經過計算機模擬、實際測試表明,基于模糊控制器的智能灌溉系統對荔枝園灌溉進行了有效控制,使荔枝園土壤含水率維持在17.8%左右,符合荔枝樹的生長環境;同時,基于優化后的模糊控制器的智能灌溉系統將荔枝園土壤含水率平均值控制在17.6%,更接近系統預設荔枝園土壤最佳含水率17%。試驗證實該系統滿足實際要求。

