三支決策空間上三支決策評(píng)價(jià)函數(shù)的構(gòu)造

胡寶清

(武漢大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 湖北 武漢 430072)

三支決策理論由姚一豫教授提出[1-3],其基本思想來自Pawlak粗糙集[4]和概率粗糙集[5-7], 基本目的是將粗糙集的正域、負(fù)域和邊界域分別解釋為一個(gè)三元分類的三個(gè)決策結(jié)果,也即,接受、拒絕和不確定(或延遲決策)。 本文系統(tǒng)研究了各類粗糙集和概率粗糙集,從三支決策的決策度量、決策條件和決策評(píng)價(jià)函數(shù)三個(gè)關(guān)鍵問題出發(fā),引入了決策評(píng)價(jià)函數(shù)的公理化定義并建立了三支決策空間[8]。 基于這一思想,筆者給出了三支決策空間上的各類三支決策,使得存在的三支決策成為三支決策空間的一些特例,例如,基于模糊集[9]、區(qū)間值模糊集[10]、區(qū)間集[11]、陰影集[12]、隨機(jī)集[13]和粗糙集的三支決策等。

三支決策空間理論引入之后,從下列幾個(gè)方面進(jìn)行了推廣研究。

1) 代數(shù)結(jié)構(gòu): 從具有否定算子的完全分配格到具有否定算子的偏序集[14-15], 這樣基于二型模糊集[16-17]、區(qū)間值二型模糊集[17-18]、猶豫集和區(qū)間猶豫集的三支決策[14]也包含在三支決策空間中。

2) 決策評(píng)價(jià)函數(shù)的構(gòu)造:從半決策評(píng)價(jià)函數(shù)到?jīng)Q策評(píng)價(jià)函數(shù)[19-20]、從多個(gè)決策評(píng)價(jià)函數(shù)到?jīng)Q策評(píng)價(jià)函數(shù)[21]的構(gòu)造方法。

本文對(duì)現(xiàn)有的決策評(píng)價(jià)函數(shù)的構(gòu)造方法進(jìn)行綜述, 并在此基礎(chǔ)上給出新的構(gòu)造方法。

1 三支決策空間的基礎(chǔ)知識(shí)

如果(X,≤)是一個(gè)偏序集, 映射N:X→X稱為強(qiáng)否定算子或逆序?qū)纤阕? 如果它滿足?x,y∈X,

1)x≤y?N(y)≤N(x) (逆序);

2)N(N(x))=x(對(duì)合律)。

算子c(xc=1-x)是[0,1]上的一個(gè)強(qiáng)否定算子。

在本文中, 我們總假設(shè)(P,≤P)是一個(gè)具有強(qiáng)否定算子NP的偏序集, 并具有最小元0P和最大元1P,一般被記為(P,≤P,NP,0P,1P)。 本文還使用下列記號(hào):

I(2)={[a-,a+]|0≤a-≤a+≤1},

I2={(a,b)|a,b∈[0,1],a+b≤1}，

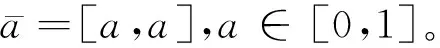
假設(shè)X和Y是兩個(gè)論域,Map(X,Y)是X到Y(jié)的映射集, 即Map(X,Y)={f|f:X→Y}。 特別地,有以下定義:

1)A∈Map(X,[0,1])是X上的一個(gè)模糊集。

2)A∈Map(X,I(2))是X上的一個(gè)區(qū)間值模糊集。一個(gè)區(qū)間值模糊集A用A=[A-,A+]表示。

3)A∈Map(X,I2)是X上的一個(gè)直覺模糊集。

4)H∈Map(X,2[0,1]-?)是X上的一個(gè)猶豫模糊集。

5)H∈Map(X,2I(2)-?)是X上的一個(gè)區(qū)間值猶豫模糊集。

6)A∈Map(X,Map([0,1],[0,1])是X上的一個(gè)二型模糊集。

7)R∈Map(X×Y,[0,1])是X到Y(jié)的一個(gè)模糊關(guān)系。

對(duì)于A∈Map(U,P),A在U中的截集定義為

Aλ={x∈U|A(x)≥Pλ},λ∈P。

補(bǔ)集定義為

NP(A)(x)=NP(A(x))。

如果A,B∈Map(U,P), 則A?PB被定義為A(x)≤PB(x), ?x∈U。 Map(U,P)中的兩個(gè)特殊元素 ?(x)=0p(?x∈U)和U(x)=1p(?x∈U), 分別記為(0p)U和(1p)U。

假設(shè)(PC,≤PC,NPC,0PC,1PC)和(PD,≤PD,NPD,0PD,1PD)是兩個(gè)偏序集,U是決策論域,V是條件論域。 我們有下面的決策評(píng)價(jià)函數(shù)的公理化定義。

定義1[14]映射

E:Map(V,PC)→Map(U,PD)

稱為U上的一個(gè)決策評(píng)價(jià)函數(shù),如果它滿足下列公理:

(E1) 最小元公理 (minimum element axiom)

E(?)=?,即E(?)(x)=0PD,?x∈U。

(E2) 單調(diào)性公理 (monotonicity axiom)

A?PCB?E(A)?PDE(B),?A,B∈Map(V,PC),即E(A)(x)≤PDE(B)(x),?x∈U。

(E3) 補(bǔ)公理 (complement axiom)

NPD(E(A))=E(NPC(A)),?A∈Map(V,PC),即NPD(E(A))(x)=E(NPC(A))(x),?x∈U。

從公理(E1)和公理(E3)可以得到

E(V)(x)=1PD,?x∈U。

基于決策評(píng)價(jià)函數(shù)的定義, 我們給出了基于偏序集的三支決策空間。

定義2[14]給定決策論域U,決策條件論域Map(V,PC), 決策度量論域PD和決策評(píng)價(jià)函數(shù)E, 稱(U,Map(V,PC),PD,E)為基于偏序集的三支決策空間。

2 基于半三支決策評(píng)價(jià)函數(shù)的三支決策評(píng)價(jià)函數(shù)構(gòu)造

在粗糙集的推廣研究中發(fā)現(xiàn)，當(dāng)?shù)葍r(jià)關(guān)系推廣到一般模糊關(guān)系時(shí), 決策評(píng)價(jià)函數(shù)不一定滿足第三條公理。 例如, 如果A是有限論域U上的一個(gè)模糊集或R是U上的一個(gè)模糊關(guān)系, 則

不一定滿足補(bǔ)公理。 這樣限制了三支決策理論的推廣應(yīng)用。 為了解決這個(gè)問題, 我們引入了半決策評(píng)價(jià)函數(shù)和半三支決策空間的概念, 并成功得到了從半決策評(píng)價(jià)函數(shù)構(gòu)造決策評(píng)價(jià)函數(shù)的方法。

定義3[19]映射

E:Map(V,PC)→Map(U,PD)

稱為U上的一個(gè)半決策評(píng)價(jià)函數(shù), 如果它滿足最小元公理(E1)和單調(diào)性公理(E2)。 同時(shí)稱(U,Map(V,PC),PD,E)為一個(gè)基于偏序集的半三支決策空間。

下面給出PD=[0,1]時(shí)的決策評(píng)價(jià)函數(shù)的構(gòu)造方法。

定理1[19]給定U上的一個(gè)半決策評(píng)價(jià)函數(shù)

E:Map(V,PC)→Map(U,[0,1])，

并且E((1PC)V)=1U。 如果α,β∈[0,1]并且α+β=1, 則

E*(A)(x)=αE(A)(x)+

β(1-E(NPC(A))(x))

是U上的一個(gè)半決策評(píng)價(jià)函數(shù)。

定理2[19]給定U上的一個(gè)半決策評(píng)價(jià)函數(shù)

E:Map(V,PC)→Map(U,[0,1])，

并且E((1PC)V)=1U。，則

E*(A)(x)=

是U上的一個(gè)決策評(píng)價(jià)函數(shù)。

下面給出了PD=I(2)時(shí)的決策評(píng)價(jià)函數(shù)的構(gòu)造方法。

定理3[19]設(shè)映射

E:Map(V,PC)→Map(U,I(2))

并且

E(A)(x)=[(E(A))-(x),(E(A))+(x)]，

則E(A)是U上的一個(gè)半決策評(píng)價(jià)函數(shù)當(dāng)且僅當(dāng)(E(A))-:Map(V,PC)→Map(U,[0,1])和(E(A))+:Map(V,PC)→Map(U,[0,1])都是U上的一個(gè)半決策評(píng)價(jià)函數(shù)。

定理4[19]設(shè)映射

E:Map(V,PC)→Map(U,I(2))

是U上的一個(gè)半決策評(píng)價(jià)函數(shù),

E(A)(x)=[(E(A))-(x),(E(A))+(x)]

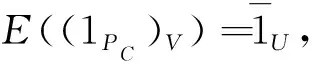
E*(A)(x)=

是U上的一個(gè)決策評(píng)價(jià)函數(shù)。

下面給出PD=I2時(shí)的決策評(píng)價(jià)函數(shù)的構(gòu)造方法。

定理5[19]設(shè)映射

E:Map(V,PC)→Map(U,I2)

并且

E(A)(x)=(Eμ(A)(x),Eν(A)(x))。

則E(A)是U上的一個(gè)半決策函數(shù)當(dāng)且僅當(dāng)

Eμ,(Eν)c:Map(V,PC)→Map(U,[0,1])

是U上的一個(gè)半決策評(píng)價(jià)函數(shù)。 如果E((1PC)V)=1I2=(1,0),則

E*(A)(x)=

是U上的一個(gè)決策評(píng)價(jià)函數(shù)。

文獻(xiàn)[19]給出了大量的從半決策評(píng)價(jià)函數(shù)到?jīng)Q策評(píng)價(jià)函數(shù)的構(gòu)造例子,這些例子來自于不同的評(píng)價(jià)條件,如模糊集、區(qū)間值模糊集、直覺模糊集、隨機(jī)集、猶豫模糊集和區(qū)間值猶豫模糊集和二型模糊集。 具有代表性的函數(shù)列入表1供讀者研究參考。

3 基于t-模和t-余模的三支決策評(píng)價(jià)函數(shù)構(gòu)造

在[0，1]上考慮t-模T和t-余模S可以構(gòu)造出更豐富的決策評(píng)價(jià)函數(shù)。

定理6[19]給定U上的一個(gè)半決策評(píng)價(jià)函數(shù)

E:Map(V,PC)→Map(U,[0,1])，

并且E((1PC)V)=1U。 則

1-E(NPC(A))(x))+S(E(A)(x),

1-E(NPC(A))(x))}

是U上的一個(gè)決策評(píng)價(jià)函數(shù), 其中T和S是[0,1]上的對(duì)偶t-模和t-余模。

當(dāng)T=min,S=max, 定理6就是定理2。

在定理6中取E(A)=A,PC=[0,1],NPC(x)=1-x, 則得到文獻(xiàn)[20]的結(jié)論:

E*(A)(x)=

是U上的一個(gè)決策評(píng)價(jià)函數(shù)。

定理7[20]設(shè)映射

E1,E2:Map(V,PC)→Map(U,[0,1])

是U上的兩個(gè)半決策評(píng)價(jià)函數(shù)，并且對(duì)所有A∈Map(V,PC)，x∈U，定義

ET(A)(x)=T(E1(A)(x),E2(A)(x))，

ES(A)(x)=S(E1(A)(x),E2(A)(x))，

E(T,S,a)(A)(x)=aET(A)(x)+

(1-a)ES(A)(x),0≤a≤1，

則ET，ES和E(T,S,a)都是U上的半決策評(píng)價(jià)函數(shù)。

定理8[20]設(shè)

E:Map(V,PC)→Map(U,[0,1])

是U上的一個(gè)半決策評(píng)價(jià)函數(shù)。 則

E(T,NPC)(A)(x)=

T(E(A)(x),1-E(NPC(A)(x))),

E(S,NPC)(A)(x)=

S(E(A)(x),1-E(NPC(A)(x)))

都是U上的半決策評(píng)價(jià)函數(shù)。

文獻(xiàn)[20]從不同的評(píng)價(jià)條件,如模糊集、區(qū)間值模糊集、猶豫模糊集等, 基于常見的模糊邏輯連接詞t-模和t-余模給出了大量的從半決策評(píng)價(jià)函數(shù)到?jīng)Q策評(píng)價(jià)函數(shù)的構(gòu)造例子。

表1 在各類決策條件下從半決策評(píng)價(jià)函數(shù)導(dǎo)出的決策評(píng)價(jià)函數(shù)

表2 在各類決策條件下基于t-模和t-余模的決策評(píng)價(jià)函數(shù)Tab.2 Three-way decision evaluation functions based on t-norm and t-conorm under various decision conditions

4 基于多個(gè)三支決策評(píng)價(jià)函數(shù)的三支決策函數(shù)構(gòu)造

設(shè)

Ei:Map(V,PC)→Map(U,[0,1]) (i=1, 2, …，n)

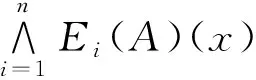
為了給出多個(gè)函數(shù)的聚合方法,先給出保補(bǔ)聚合函數(shù)的概念。

定義4[21]設(shè)(P,≤P,NP,0P,1P)是一個(gè)有界偏序集, 則映射f:Pn→P稱為一個(gè)n元保補(bǔ)聚合函數(shù), 如果它滿足下列條件

(AF1) 正則性:

f(x,x,…,x)=x, ?x∈P;

(AF2) 遞增性:

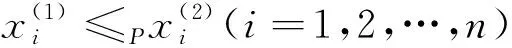
(AF3) 保補(bǔ)性:

f(NP(x1),NP(x2),…,NP(xn))=

NP(f(x1,x2,…,xn)),?xi∈P。

記P上所有n元保補(bǔ)聚合函數(shù), 記為AFn(P)。

以下考慮多個(gè)決策評(píng)價(jià)函數(shù)的聚合。

定理9[21]設(shè)映射

Ei:Map(V,PC)→Map(U,PD)(i=1, 2, …，n)是U上的n個(gè)決策評(píng)價(jià)函數(shù),f∈AFn(PD)并且對(duì)所有A∈Map(V,PC)和x∈U,

Ef(A)(x)=

f(E1(A)(x),E2(A)(x),…,En(A)(x))，

則(U,Map(V,PC),PD,Ef)是U上的一個(gè)三支決策評(píng)價(jià)函數(shù)。

下面是一些對(duì)PD=[0,1]的聚合三支決策評(píng)價(jià)函數(shù)的例子。

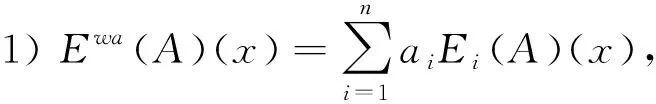
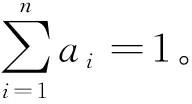
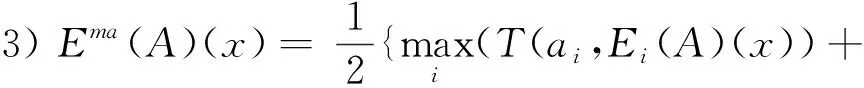
4)Eme(A)(x)=Median{Ei(A)(x)}, 其中Median是中位數(shù)。

5 決策評(píng)價(jià)函數(shù)新構(gòu)造方法

在前面構(gòu)造方法的啟發(fā)下, 下面給出新的構(gòu)造方法。 因決策評(píng)價(jià)函數(shù)可由定理2通過半決策評(píng)價(jià)函數(shù)構(gòu)造得到, 所以下面只給出半決策評(píng)價(jià)函數(shù)的構(gòu)造。

定理10設(shè)A∈Map(V,[0,1]),R∈Map(U×V,[0,1]), 定義映射

E:Map(V,[0,1])→Map(U,[0,1]),

則E是U上的一個(gè)半決策評(píng)價(jià)函數(shù)并且E(1V)=1U。

證明顯然滿足最小元公理和單調(diào)性公理。 對(duì)所有x∈U,

E(1V)(x)=

定理11設(shè)A∈Map(V,[0,1]),R∈Map(U×V,[0,1]), 定義映射

E:Map(V,[0,1])→Map(U,[0,1])

S(A(y),R(x,y)))

則E是U上的一個(gè)半決策評(píng)價(jià)函數(shù)，并且E(1V)=1U。

證明顯然滿足最小元公理和單調(diào)性公理。 對(duì)所有x∈U,

E(1V)(x)=

例1在定理10和定理11中, 如果考慮S=∨,T=∧, 則

這其實(shí)是模糊集A的相對(duì)基數(shù)。 由定理2得到?jīng)Q策評(píng)價(jià)函數(shù)

例2在定理10中, 如果考慮

S(x,y)=(x+y)∧1,

T(x,y)=(x+y-1)∨0,

則

E(A)(x)=

(A(y)+R(x,y)-1)∨0)∧1。

由定理2得到?jīng)Q策評(píng)價(jià)函數(shù)

(R(x,y)-A(y))∨0)∧1]}。

取

U=V={x1,x2,x3,x4,x5},

則

定理10和定理11的結(jié)論可推廣到其他決策條件上。

定理12設(shè)A∈Map(V,I(2)),R∈Map(U×V,I(2)), 定義映射

E1,E2:Map(V,I(2))→Map(U,[0,1])，

E1(A)(x)=

y))),

E2(A)(x)=

y)))

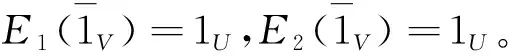
定理13設(shè)A∈Map(V,I(2)),R∈Map(U×V,I(2)), 定義映射

E1,E2:Map(V,I(2))→Map(U,I(2))，

E1(A)(x)=

E2(A)(x)=

6 結(jié) 語

本文討論的是三支決策空間理論中一個(gè)很重要的結(jié)論,可以從只滿足公理(E1)和(E2)的函數(shù)出發(fā)構(gòu)造滿足公理(E1)，(E2)和(E3)的函數(shù)。 首先, 從不同角度回顧了一系列構(gòu)造方法。 其次, 基于論域的基數(shù)給出了決策評(píng)價(jià)函數(shù)新的構(gòu)造方法。

關(guān)于三支決策的構(gòu)造還可以從以下幾個(gè)方面進(jìn)行考慮:

1) 將強(qiáng)否定算子放寬到否定算子上,即去掉對(duì)合律,這樣使用更加廣泛。

2) 基于一致模和零模等推廣模的決策評(píng)價(jià)函數(shù)構(gòu)造。

3) 半決策評(píng)價(jià)函數(shù)到?jīng)Q策評(píng)價(jià)函數(shù)主要是在[0,1]或I(2)上, 能否在偏序集上直接從半決策評(píng)價(jià)函數(shù)構(gòu)造出決策評(píng)價(jià)函數(shù)?