超聲檢測中金屬裂紋多特征提取研究

樊 萍，劉新寶

(1.西北大學 信息科學與技術學院，陜西 西安 710127;2.西北大學 化工學院，陜西 西安 710069)

隨著工業生產技術的不斷進步,越來越多的金屬構件被用于工業裝備制造。長期服役的金屬構件中會出現裂紋,這些裂紋在應力作用下不斷加速擴展,最終造成機械設備損毀和工程結構斷裂。因此準確檢測和識別金屬裂紋成為保證裝備運行安全的首要前提。

由于自身的非破壞性,超聲檢測現已成為一種最常用的無損檢測方法[1-2]。然而,超聲回波信號具有典型的時變、非平穩特性,導致傳統的信號處理方法很難實現對裂紋的特征提取與精準識別[3-4]。由于小波分析具有多分辨分析的特點,使其能同時在時域和頻域表征信號的局部特征,因而在非平穩信號處理中得到了廣泛應用[5-7]。Anaya等人將離散小波變換和神經網絡相結合,完成了金屬鋁板內部不同損傷的分類識別[8];Ali等人比較了連續小波變換和小波包變換中小波函數選取對裂紋分類結果的影響[9]。

然而已有研究大多僅選用小波變換系數作為裂紋特征[10-11],對裂紋信息的表征能力有限,且容易受到噪聲干擾。針對這些問題，本文首先對超聲回波進行小波包變換，在分析信號時頻域信息的基礎上，定義能量熵、模極大值和相關系數等參數作為識別特征；接著,結合相關算法實現對裂紋的識別。此外，通過對3種不同尺寸的金屬裂紋進行超聲反射法回波實驗，以驗證該方法的有效性。

1 小波包變換

已有研究顯示,超聲回波信號的高頻部分和低頻部分均包含裂紋的相關信息[8-9]。只有對信號低頻和高頻部分同時處理,才能實現對裂紋的全面表征。常用的離散小波變換僅對信號的低頻部分逐層分解,而對高頻部分不做處理。相比之下,小波包變換[12]對信號的低頻和高頻部分同時進行多層次分解,顯著提高了信號的時頻分辨率。對于正交小波包變換,設{Uj,n,k(t)}k∈Z是空間Uj,n的標準正交基,信號y(t)在空間Uj,n上的投影yj,n(t)為

(1)

其中，dj,n(t)=〈y(t),uj,n,k(t)〉為小波包系數。由于空間Uj,n可以分解為Uj+1,2n和Uj+1,2n+1的標準正交基{Uj+1,2n,k(t)}k∈Z和{Uj+1,2n+1,k(t)}k∈Z，由二尺度方程可得

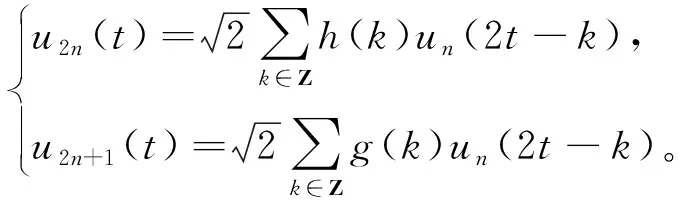
(2)

其中，尺度函數φ(t)和小波函數φ(t)分別記為φ(t)=u0(t)，φ(t)=u1(t)。g(k)，h(k)是一組與尺度函數和小波函數相關聯的正交鏡像濾波器組,g(k)=(-1)kh(1-k)。上式定義的函數集合{Un(t)}k∈Z是由u0(t)=φ(t)確定的正交小波包。當n=0時

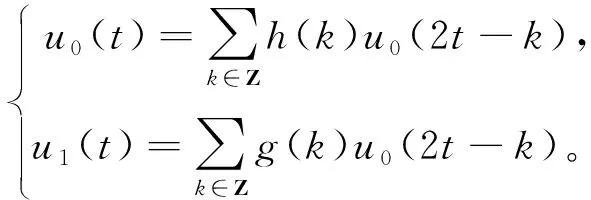
(3)

對式(3)中等號兩邊與y(t)做內積,得到

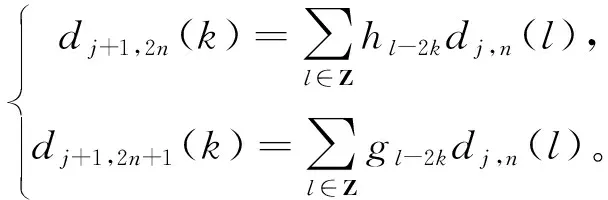
(4)

式(4)即為超聲回波信號經過小波包分解后對應的低頻和高頻小波包函數表達式。

2 金屬裂紋多特征提取

作為超聲檢測的核心步驟,定義適當的特征參數實現對裂紋信息的全面表征至關重要。本文在上述回波信號小波包變換的基礎上,定義如下3個裂紋特征參數。

2.1 相關系數

相關系數描述了兩個隨機信號之間的相似程度[13]。金屬裂紋造成超聲回波信號和正常信號在某些頻段內存在差異,相似度降低。因此,定義超聲檢測中回波信號和無裂紋正常信號在相同頻段范圍內的互相關系數為

(5)

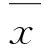
(6)

2.2 能量熵

能量熵是時頻域小波包能量規律性的量度[14]。能量熵值越大,信號中各成分的不確定性越大,所包含的信息量越大;能量熵值越小,信號所包含的信息量也越少。因此,定義小波包信號的能量熵為裂紋的第2個特征參數,

H(e)=eilogei。

(7)

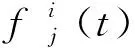
2.3 模極大值

超聲回波信號中劇烈變化的部分往往與裂紋有關[15]，這些不規則的信號突變點稱為奇異點,反映了超聲波在金屬內部的傳播特性。已有研究顯示,小波變換后的模極大值正好與信號的奇異點相對應[16]。因此,定義小波包變換后模極大值時的幅度和時間作為裂紋的第3個特征,

F={(A1,T1), (A2,T2), …,(Am,Tm)}。

(8)

3 實驗及結果分析

為了驗證上述裂紋特征提取方法的有效性,本文對同一金屬板上不同尺寸的裂紋進行超聲檢測實驗。如圖1所示,金屬板有效長度50mm(兩個頂肩之間距離)、寬度15mm、厚度2mm。測試中C0表示無裂紋時的正常狀態,其他裂紋狀態是在上表面的不同位置上采用線切割加工而成的通孔,這些不同橫截面大小的通孔從左到右分別為C1(0.8mm×0.8mm)，C2(1.2mm×1.2mm)，C3(1.6mm×1.6mm)。超聲檢測系統包括Olympus的5073PR脈沖收發器、Agilent的2022A 示波器以及Panametric中心頻率為10MHz、直徑為6mm的V112-RM接觸式高頻直探頭,為了避免該高頻探頭的近場區影響和邊界效應,檢測時在探頭前面附加了延時塊。在開始測量前,把圖1中的金屬板翻轉過來使得有通孔裂紋的一面朝下,然后超聲波從上表面進入,圖2截取了從底面一次反射回來的不同裂紋超聲回波信號。從圖2中可以看出,在1.05×10-6s處均出現明顯的超聲回波。根據上述測試過程可知,該回波為金屬板材底面的一次反射波。隨著裂紋尺寸的增加,直接從底面反射回來的有效面積減少,導致其反射波幅度降低。同時,圖2(b)～(d)中分別在8×10-7s，7×10-7s，5.5×10-7s隱約出現了裂紋回波信號,主要是由于探頭到3個橫孔的聲程逐漸減小所致。然而,要直接對這3種裂紋類型實現識別卻比較困難,必須進行裂紋特征提取。

圖1 超聲檢測試樣Fig.1 Ultrasonic testing of plate sample of steel

對采集到的超聲回波信號首先進行小波包分解，通過比較分析選取db5為小波包基函數。在此基礎上,結合式(5)～(8)分別對不同金屬裂紋的回波信號進行了多特征提取,其計算結果如圖3所示。從圖3中可以看出,隨著裂紋尺寸的增加,在等節點上相關系數逐漸減小，特別是在較小節點處差別顯著。同時，模極大值特征在不同時間點上出現的次數明顯增加。此外，由于裂紋尺寸的不同，能量熵特征的峰值在各個節點上也存在差異。因此可見,上述3種特征均可用于表征具有截面尺寸差異的C1，C2和C3裂紋。

為了全面表征金屬裂紋狀態,進一步提高識別率,本文采用k-近鄰分類方法[17]和D-S證據理論[18]決策級融合相結合對上述3類裂紋進行識別,具體識別方法如圖4所示。實驗對金屬板無裂紋正常狀態和3類裂紋狀態分別隨機采集60個點的超聲波檢測數據，其中40個數據樣本組成訓練庫,其余數據作為測試樣本。

利用上述3個特征分別進行金屬裂紋識別的結果和多特征融合識別結果如圖5所示。

可以看出,本文定義的相關系數、能量熵和模極大值3種特征都能夠實現金屬裂紋識別。隨著裂紋尺寸的增大,基于上述特征的金屬裂紋識別率相應提高。由于相關系數采用無裂紋正常狀態的超聲回波信號做參考，更適合于描述小裂紋,因此，針對C1裂紋該特征的單一識別率最高。裂紋尺寸的增加使得超聲回波信號的突變更為明顯,不同裂紋間模極大值的差異更加顯著,因此基于該特征的C3識別率最高。綜合上述3個特征進行決策級融合識別時,裂紋識別率普遍提高。裂紋尺寸越小,識別率提高越顯著,最小裂紋C1的多特征識別率高達92%。由此可見,本文提出的多特征能更好地描述裂紋信息,為不同尺寸裂紋的準確識別提供依據。

為了進一步驗證噪聲對上述裂紋特征的影響,在實驗數據中分別加入SNR為10dB，15dB和20dB的零均值高斯白噪聲，3類裂紋識別率如圖6所示。很明顯,噪聲對裂紋識別率影響不大。在SNR=10dB的低信噪比情況下,不同裂紋的多特征平均識別率仍然達到83%。因此,上述3種裂紋特征對高斯白噪聲不敏感,更適用于工業裝備運行狀態的安全無損檢測。

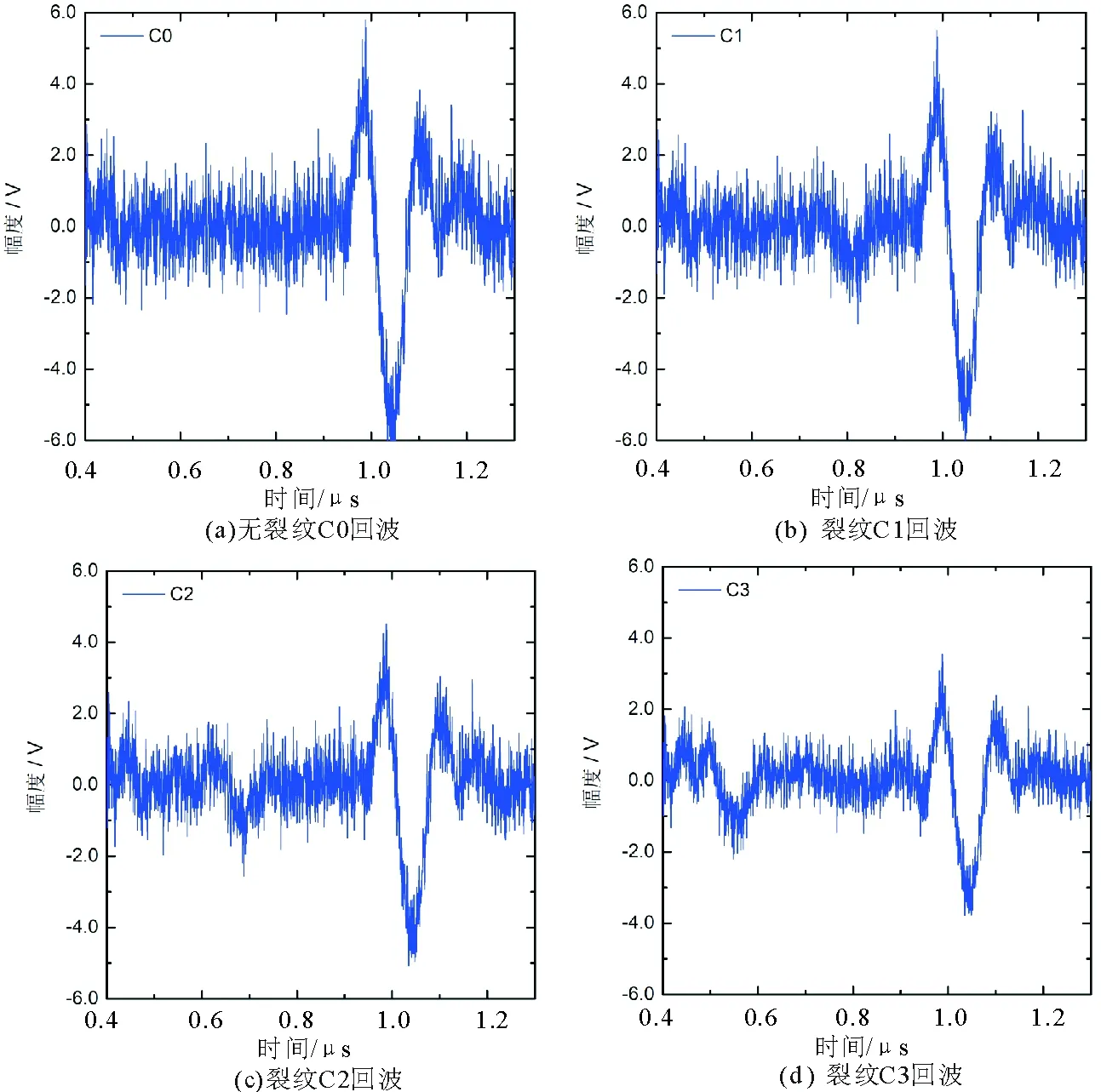
圖2 不同裂紋的超聲回波信號Fig.2 Obtained ultrasonic echoes of different cracks

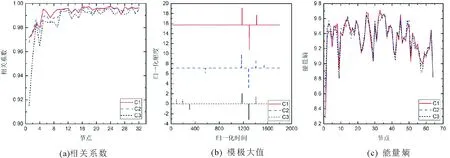
圖3 3種金屬構件裂紋多特征提取Fig.3 Multi-feature extraction of three metal cracks

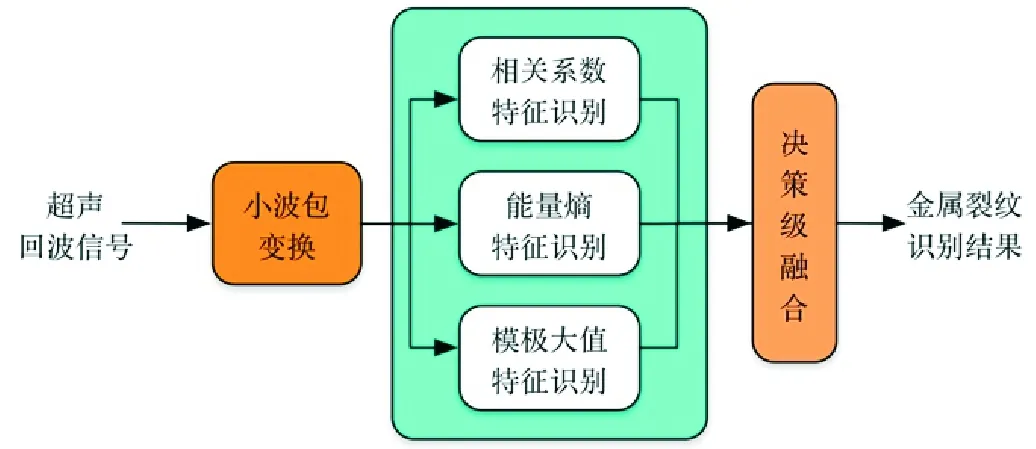
圖4 金屬裂紋識別方法Fig.4 Proposed method for metal crack identification

圖5 基于不同特征的金屬裂紋識別率Fig.5 Metal crack identification with different features

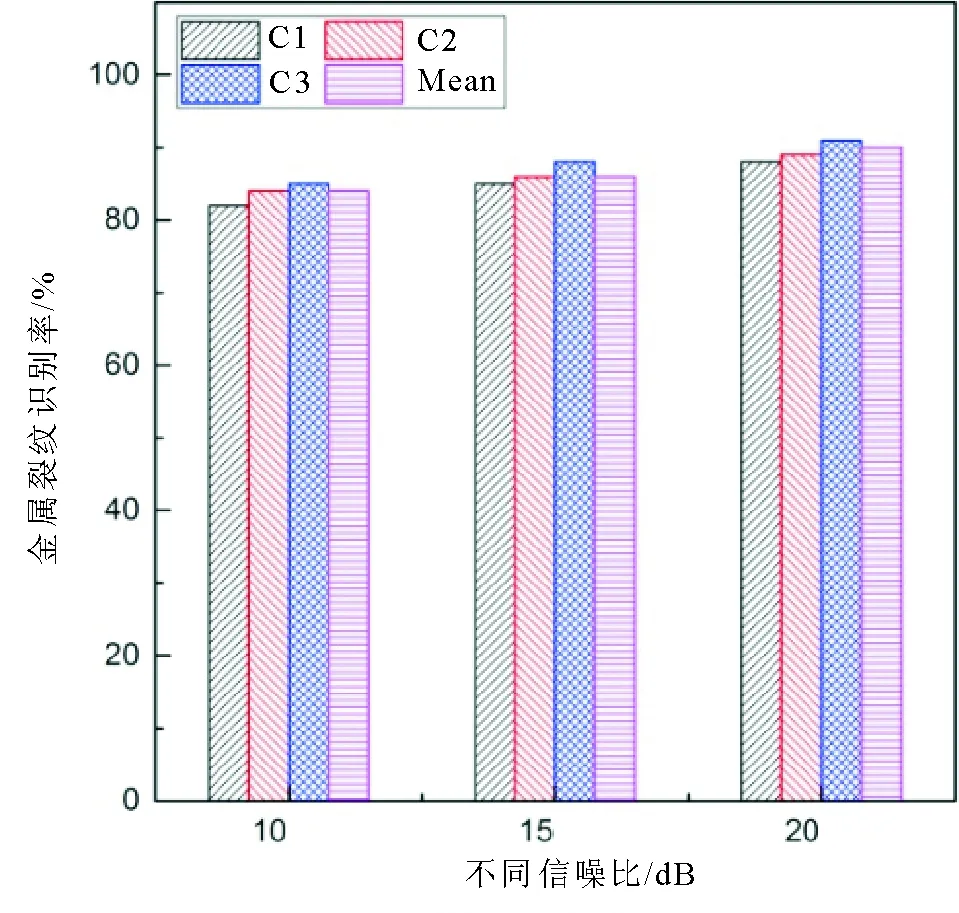
圖6 不同信噪比下金屬裂紋識別率Fig.6 Metal crack identification under different values of SNR

4 結 論

針對目前超聲檢測中常用的金屬裂紋識別方法特征單一、容易受到噪聲干擾等問題,為了進一步提高超聲檢測的準確性，本文提出了一種基于多特征提取的金屬裂紋檢測方法。在對超聲回波信號進行小波包變換的基礎上,分別定義相關系數、能量熵和模極大值作為特征用于金屬裂紋的識別。此外，利用本文方法對金屬板上3種不同尺寸的裂紋進行超聲檢測。結果表明,基于上述多特征的金屬裂紋識別結果顯著提高,而且對高斯白噪聲不敏感,因而更適用于實際工業設備的安全運行檢測。